5.3 图形变换的简单应用 同步练习
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
5.3 图形变换的简单应用
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一.选择题(共5小题,每题6分)
1.下列四幅图案可以看作是以图案中某部分为基本图形平移得到的是( )
A. B.
C. D.
2.在中国集邮总公司设计的2017年纪特邮票首日纪念戳图案中,可以看作中心对称图形的是( )
A. B.
C. D.
3.如图,用数学的眼光欣赏这个蝴蝶图案,它的一种数学美体现在蝴蝶图案的( )
A.轴对称性 B.蝴蝶效应 C.颜色鲜艳 D.数形结合
4.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )
A.1种 B.2种 C.3种 D.4种
5.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
A. B.
C. D.
二.填空题(共5小题,每题6分)
6.在下列图案中可以用平移得到的是 (填代号).
7.如图是由9个小等边三角形构成的图形,其中已有两个被涂黑,若再涂黑一个,则整个被涂黑的图案构成轴对称图形的方法有 种.
8.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转 次,每次旋转 度形成的.
9.如图可以看作是由基本图形 经 得到的.
10.如图,第1个图案是由同样规格的黑白两种颜色的正方形地砖组成,第2个、第3个图案可以看做是第1个图案经过平移得到的,那么第n个图案中需要黑色正方形地砖 块(用含n的式子表示).
三.解答题(共3小题,第11、12题每题12分,第13题16分)
11.如图,平移方格纸中的图形,使点A平移到点A′处,画出平移后的图形.
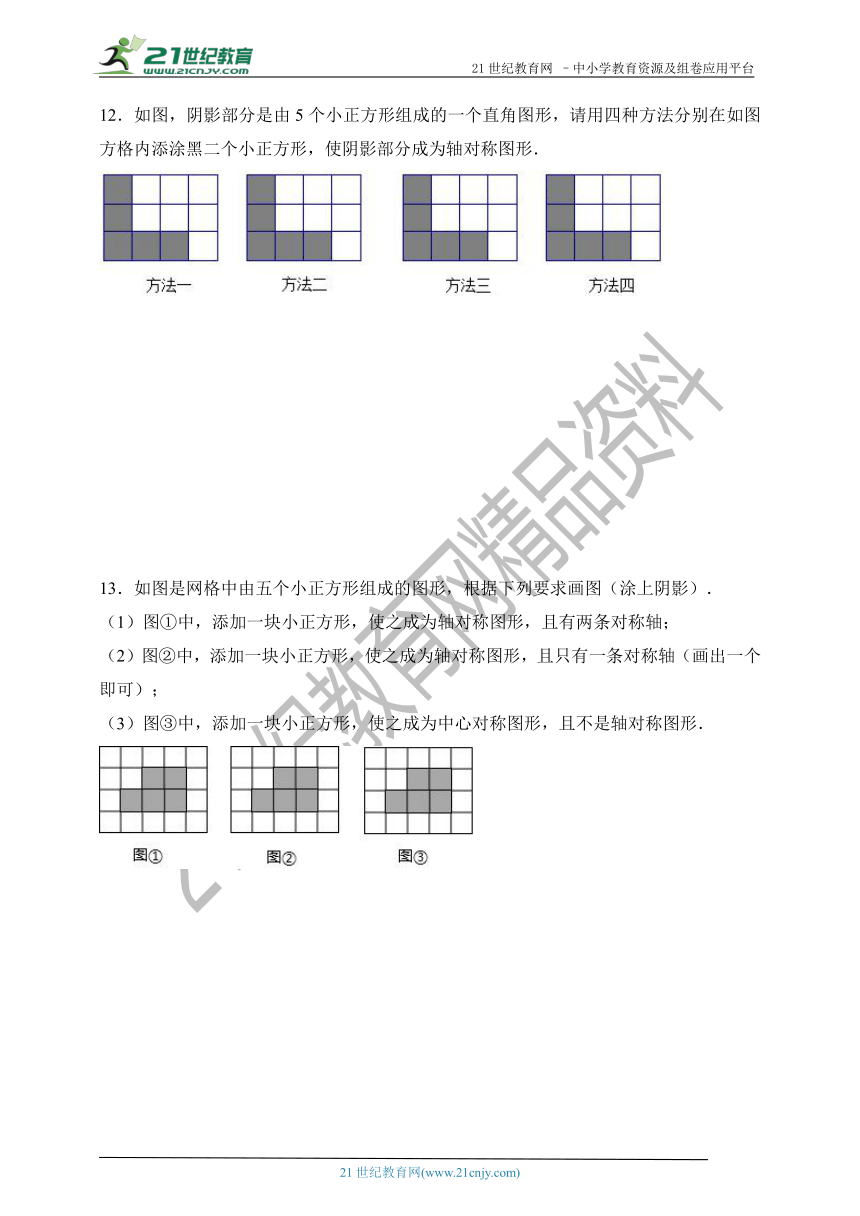
12.如图,阴影部分是由5个小正方形组成的一个直角图形,请用四种方法分别在如图方格内添涂黑二个小正方形,使阴影部分成为轴对称图形.
13.如图是网格中由五个小正方形组成的图形,根据下列要求画图(涂上阴影).
(1)图①中,添加一块小正方形,使之成为轴对称图形,且有两条对称轴;
(2)图②中,添加一块小正方形,使之成为轴对称图形,且只有一条对称轴(画出一个即可);
(3)图③中,添加一块小正方形,使之成为中心对称图形,且不是轴对称图形.
试题解析
一.选择题
1. C
【分析】根据图形平移的性质即可得出结论.
【解答】解:A、利用图形旋转而成,不符合题意;
B、利用轴对称而成,不符合题意;
C、利用图形平移而成,符合题意;
D、利用图形旋转而成,不符合题意.
故选:C.
【点评】本题考查的是利用平移设计图案,熟知图形平移不变性的性质是解答此题的关键.
2.C
【分析】根据中心对称图形的概念求解.
【解答】解:A选项是轴对称图形,不是中心对称图形,故本选项错误;
B选项不是中心对称图形,故本选项错误;
C选项为中心对称图形,故本选项正确;
D选项不是中心对称图形,故本选项错误.
故选:C.
【点评】本题主要考查了中心对称图形的概念:关键是找到相关图形的对称中心,旋转180度后与原图重合.
3.A
【分析】直接利用图形的形状以及对称性分析得出答案.
【解答】解:用数学的眼光欣赏这个蝴蝶图案,它的一种数学美体现在蝴蝶图案的轴对称性.
故选:A.
【点评】此题主要考查了利用轴对称设计图案,正确利用图形的对称性分析是解题关键.
4.C
【分析】根据轴对称图形的概念:把一个图形沿着某条直线折叠,直线两旁的部分能够完全重合及正方形的对称轴是两条对角线所在的直线和两组对边的垂直平分线,得出结果.
【解答】解:在1,2,3处分别涂黑都可得一个轴对称图形.
故选:C.
【点评】考查了利用轴对称设计图案,此题要首先找到大正方形的对称轴,然后根据对称轴,进一步确定可以涂黑的正方形.
5.B
【分析】根据轴对称和旋转的性质即可得到结论.
【解答】解:先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是B,
故选:B.
【点评】本题考查了轴对称和旋转的性质,正确的识别图形是解题的关键.
二.填空题
6.③④⑤
【分析】根据图形平移的性质即可得出结论.
【解答】解:①、②、⑥通过旋转得到;③、④、⑤通过平移得到.
故答案为:③④⑤
【点评】本题考查的是利用平移设计图案,熟知图形平移不变性的性质是解答此题的关键.
7.3
【分析】根据轴对称的概念作答.如果一个图形沿一条直线对折,直线两旁的部分能互相重合,那么这个图形叫做轴对称图形.
【解答】解:如图所示:将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有3种.
故答案为:3.
【点评】本题考查了利用轴对称设计图案的知识,关键是掌握好轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
9.【分析】观察图形,根据旋转的意义,可以看出图形是如何得到的.
【解答】解:根据旋转的意义,正方形AGOF围绕O点顺时针旋转90°可得到正方形OFDE,再旋转90°,可得到正方形OECH,因此可以看作是由基本图形正方形AGOF经绕点O旋转得到的.
【点评】本题考查了图形的旋转变化,学生主要要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错.
10.(3n+1)
【分析】找出数量上的变化规律,从而推出一般性的结论.
【解答】解:第一个图形有黑色瓷砖3+1=4块.
第二个图形有黑色瓷砖3×2+1=7块.
第三个图形有黑色瓷砖3×3+1=10块.
…
第n个图形中需要黑色瓷砖3n+1块.
故答案为:(3n+1).
【点评】此题主要考查了图形的变化,关键是通过归纳与总结,得到其中的规律.
三.解答题
11.【分析】先根据A、A′的位置关系,找出平移的规律,作出各个关键点的对应点,连接即可.
【解答】解:
【点评】本题的关键是根据已知对应点的位置找平移的规律.
12.【分析】如图,在四个图形中分别将两个小正方形涂黑,并使阴影部分成为轴对称图形.
【解答】解:如图所示:
【点评】本题考查了轴对称的性质和图案设计,熟练掌握轴对称的定义是关键,涂黑二个小正方形后,以是否沿一条直线折叠后能重合,作为依据,能则组成轴对称图形,反之则不能.
13.【分析】(1)直接利用轴对称图形的性质结合对称轴的条数进而得出答案;
(2)直接利用轴对称图形的性质结合对称轴的条数进而得出答案;
(3)直接利用中心对称图形的性质进而得出答案.
【解答】解:(1)如图①所示:
(2)如图②所示:
(3)如图③所示:
【点评】此题主要考查了利用轴对称和利用中心对称设计图案,正确掌握轴对称图形的性质是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.3 图形变换的简单应用
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一.选择题(共5小题,每题6分)
1.下列四幅图案可以看作是以图案中某部分为基本图形平移得到的是( )
A. B.
C. D.
2.在中国集邮总公司设计的2017年纪特邮票首日纪念戳图案中,可以看作中心对称图形的是( )
A. B.
C. D.
3.如图,用数学的眼光欣赏这个蝴蝶图案,它的一种数学美体现在蝴蝶图案的( )
A.轴对称性 B.蝴蝶效应 C.颜色鲜艳 D.数形结合
4.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )
A.1种 B.2种 C.3种 D.4种
5.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
A. B.
C. D.
二.填空题(共5小题,每题6分)
6.在下列图案中可以用平移得到的是 (填代号).
7.如图是由9个小等边三角形构成的图形,其中已有两个被涂黑,若再涂黑一个,则整个被涂黑的图案构成轴对称图形的方法有 种.
8.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转 次,每次旋转 度形成的.
9.如图可以看作是由基本图形 经 得到的.
10.如图,第1个图案是由同样规格的黑白两种颜色的正方形地砖组成,第2个、第3个图案可以看做是第1个图案经过平移得到的,那么第n个图案中需要黑色正方形地砖 块(用含n的式子表示).
三.解答题(共3小题,第11、12题每题12分,第13题16分)
11.如图,平移方格纸中的图形,使点A平移到点A′处,画出平移后的图形.
12.如图,阴影部分是由5个小正方形组成的一个直角图形,请用四种方法分别在如图方格内添涂黑二个小正方形,使阴影部分成为轴对称图形.
13.如图是网格中由五个小正方形组成的图形,根据下列要求画图(涂上阴影).
(1)图①中,添加一块小正方形,使之成为轴对称图形,且有两条对称轴;
(2)图②中,添加一块小正方形,使之成为轴对称图形,且只有一条对称轴(画出一个即可);
(3)图③中,添加一块小正方形,使之成为中心对称图形,且不是轴对称图形.
试题解析
一.选择题
1. C
【分析】根据图形平移的性质即可得出结论.
【解答】解:A、利用图形旋转而成,不符合题意;
B、利用轴对称而成,不符合题意;
C、利用图形平移而成,符合题意;
D、利用图形旋转而成,不符合题意.
故选:C.
【点评】本题考查的是利用平移设计图案,熟知图形平移不变性的性质是解答此题的关键.
2.C
【分析】根据中心对称图形的概念求解.
【解答】解:A选项是轴对称图形,不是中心对称图形,故本选项错误;
B选项不是中心对称图形,故本选项错误;
C选项为中心对称图形,故本选项正确;
D选项不是中心对称图形,故本选项错误.
故选:C.
【点评】本题主要考查了中心对称图形的概念:关键是找到相关图形的对称中心,旋转180度后与原图重合.
3.A
【分析】直接利用图形的形状以及对称性分析得出答案.
【解答】解:用数学的眼光欣赏这个蝴蝶图案,它的一种数学美体现在蝴蝶图案的轴对称性.
故选:A.
【点评】此题主要考查了利用轴对称设计图案,正确利用图形的对称性分析是解题关键.
4.C
【分析】根据轴对称图形的概念:把一个图形沿着某条直线折叠,直线两旁的部分能够完全重合及正方形的对称轴是两条对角线所在的直线和两组对边的垂直平分线,得出结果.
【解答】解:在1,2,3处分别涂黑都可得一个轴对称图形.
故选:C.
【点评】考查了利用轴对称设计图案,此题要首先找到大正方形的对称轴,然后根据对称轴,进一步确定可以涂黑的正方形.
5.B
【分析】根据轴对称和旋转的性质即可得到结论.
【解答】解:先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是B,
故选:B.
【点评】本题考查了轴对称和旋转的性质,正确的识别图形是解题的关键.
二.填空题
6.③④⑤
【分析】根据图形平移的性质即可得出结论.
【解答】解:①、②、⑥通过旋转得到;③、④、⑤通过平移得到.
故答案为:③④⑤
【点评】本题考查的是利用平移设计图案,熟知图形平移不变性的性质是解答此题的关键.
7.3
【分析】根据轴对称的概念作答.如果一个图形沿一条直线对折,直线两旁的部分能互相重合,那么这个图形叫做轴对称图形.
【解答】解:如图所示:将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有3种.
故答案为:3.
【点评】本题考查了利用轴对称设计图案的知识,关键是掌握好轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
9.【分析】观察图形,根据旋转的意义,可以看出图形是如何得到的.
【解答】解:根据旋转的意义,正方形AGOF围绕O点顺时针旋转90°可得到正方形OFDE,再旋转90°,可得到正方形OECH,因此可以看作是由基本图形正方形AGOF经绕点O旋转得到的.
【点评】本题考查了图形的旋转变化,学生主要要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错.
10.(3n+1)
【分析】找出数量上的变化规律,从而推出一般性的结论.
【解答】解:第一个图形有黑色瓷砖3+1=4块.
第二个图形有黑色瓷砖3×2+1=7块.
第三个图形有黑色瓷砖3×3+1=10块.
…
第n个图形中需要黑色瓷砖3n+1块.
故答案为:(3n+1).
【点评】此题主要考查了图形的变化,关键是通过归纳与总结,得到其中的规律.
三.解答题
11.【分析】先根据A、A′的位置关系,找出平移的规律,作出各个关键点的对应点,连接即可.
【解答】解:
【点评】本题的关键是根据已知对应点的位置找平移的规律.
12.【分析】如图,在四个图形中分别将两个小正方形涂黑,并使阴影部分成为轴对称图形.
【解答】解:如图所示:
【点评】本题考查了轴对称的性质和图案设计,熟练掌握轴对称的定义是关键,涂黑二个小正方形后,以是否沿一条直线折叠后能重合,作为依据,能则组成轴对称图形,反之则不能.
13.【分析】(1)直接利用轴对称图形的性质结合对称轴的条数进而得出答案;
(2)直接利用轴对称图形的性质结合对称轴的条数进而得出答案;
(3)直接利用中心对称图形的性质进而得出答案.
【解答】解:(1)如图①所示:
(2)如图②所示:
(3)如图③所示:
【点评】此题主要考查了利用轴对称和利用中心对称设计图案,正确掌握轴对称图形的性质是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
