1.2 长度和时间的测量 复习(沪粤版八年级)
文档属性
| 名称 | 1.2 长度和时间的测量 复习(沪粤版八年级) |
|
|
| 格式 | rar | ||
| 文件大小 | 58.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪粤版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2009-08-06 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
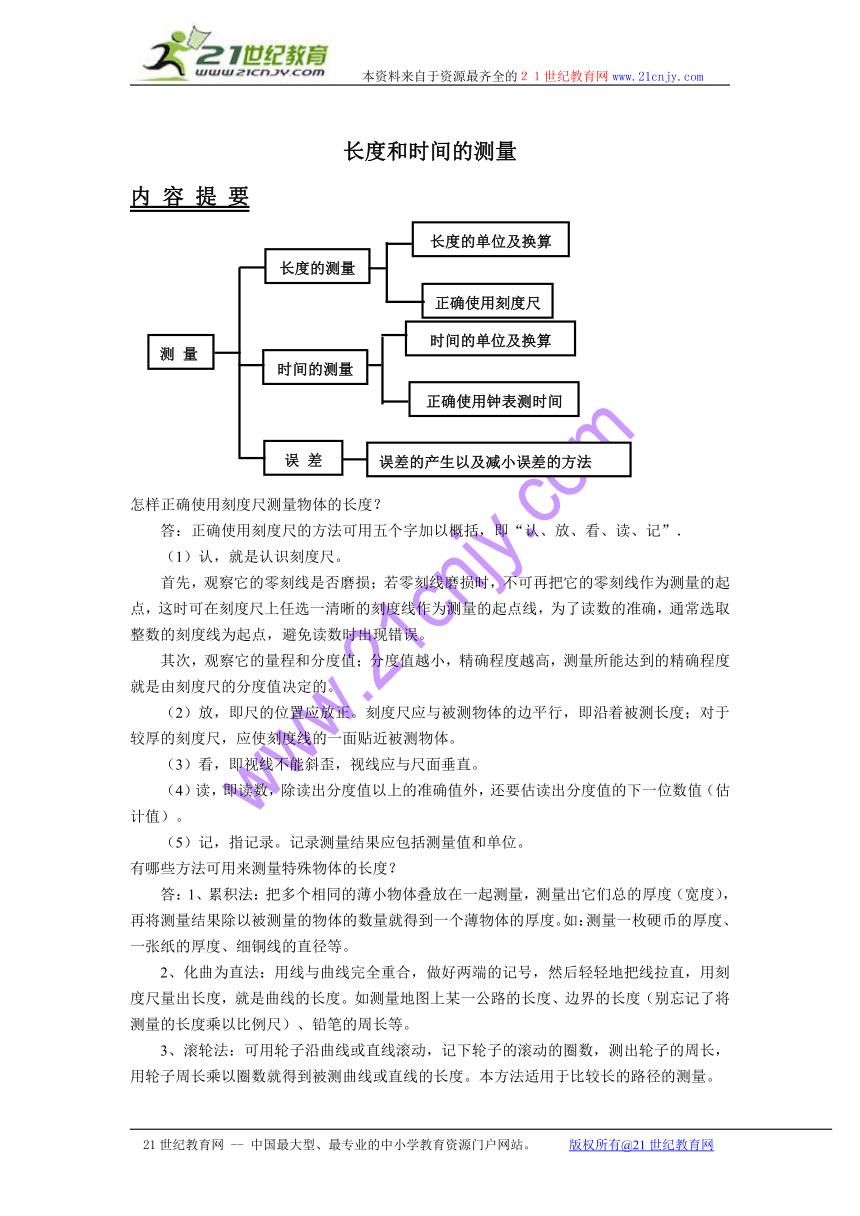
长度和时间的测量
内 容 提 要
怎样正确使用刻度尺测量物体的长度?
答:正确使用刻度尺的方法可用五个字加以概括,即“认、放、看、读、记”.
(1)认,就是认识刻度尺。
首先,观察它的零刻线是否磨损;若零刻线磨损时,不可再把它的零刻线作为测量的起点,这时可在刻度尺上任选一清晰的刻度线作为测量的起点线,为了读数的准确,通常选取整数的刻度线为起点,避免读数时出现错误。
其次,观察它的量程和分度值;分度值越小,精确程度越高,测量所能达到的精确程度就是由刻度尺的分度值决定的。
(2)放,即尺的位置应放正。刻度尺应与被测物体的边平行,即沿着被测长度;对于较厚的刻度尺,应使刻度线的一面贴近被测物体。
(3)看,即视线不能斜歪,视线应与尺面垂直。
(4)读,即读数,除读出分度值以上的准确值外,还要估读出分度值的下一位数值(估计值)。
(5)记,指记录。记录测量结果应包括测量值和单位。
有哪些方法可用来测量特殊物体的长度?
答:1、累积法:把多个相同的薄小物体叠放在一起测量,测量出它们总的厚度(宽度),再将测量结果除以被测量的物体的数量就得到一个薄物体的厚度。如:测量一枚硬币的厚度、一张纸的厚度、细铜线的直径等。
2、化曲为直法:用线与曲线完全重合,做好两端的记号,然后轻轻地把线拉直,用刻度尺量出长度,就是曲线的长度。如测量地图上某一公路的长度、边界的长度(别忘记了将测量的长度乘以比例尺)、铅笔的周长等。
3、滚轮法:可用轮子沿曲线或直线滚动,记下轮子的滚动的圈数,测出轮子的周长,用轮子周长乘以圈数就得到被测曲线或直线的长度。本方法适用于比较长的路径的测量。
什么叫误差?它跟错误有什么不同?如何减小测量误差?
答:(1)测量值跟其实值之间的差异叫误差,误差是测量中不可避免的。误差的产生是由于测量过程中受到主观或客观因素的影响造成的。
测量错误是在测量中采用了错误的方法、错误的仪器、错误的使用方法、错误的读数方法和记录方法造成的,它时可以避免而且时必须避免的。
(2)减小误差的方法有很多,我们可以通过校准测量仪器、改进出来方法、选精确度高的仪器、多次测量取平均值等,都可以减小测量误差。
长度的单位换算时要注意什么?
答:单位换算,实际上是换算单位,要注意记住各单位之间的换算关系。数字照抄,把相应的单位作等量代换。另外,单位换算过程中都用乘法,且要确保等式前后相等。如:
5.2m=5.2×100cm=520cm(红色的100cm就表示1m)
如何才能进行比较准确的估测?
答:课程标准要求培养学生的估测能力,在现实生活中,估测能力也是非常必要的。要提高估测能力,首先要借助具体事物对1m、1dm、1cm、1mm等长度形成具体的模型,头脑里对这些长度要有比较清晰的印象,二是要记住一些具体的事物的长度,如手的一拃的长度、自己的身高等,同时也可以采用身边具体事物的长度来帮助判断分析,也就是要将理论与实际联系起来。当然,平时也要注意多想一想,多比一比,测一测,都有助于提高自己的估测的准确性。
知 识 归 类
最近几年,中考题中对测量的知识的考查主要是长度的正确测量方法与读数、误差的性质及减小误差的方法、常见长度的认识、单位换算以及在其它实验探究中涉及的时间长度测量的仪器选择等。多出现在填空、选择题和实验探究题中。
题型一:主要考查对长度单位的认识以及长度单位的换算问题
例1:一名粗心的学生在测量记录中忘记记录下单位,那么在他记录的下列数据中,哪一个数据的单位是m
A.一支新铅笔的长度:0.175 B.一名同学的高度:1.64
C.一枚壹角硬币的厚度0.24 D.一本外文字典的厚度1.35
点拨:一支新铅笔的长度约为10~20cm,0.175m=17.5cm,因而A选项是正确的。B、C、D若以m为单位,显然是不符合生活常识,是错误的。 因材,在判断分析过程中,一定要将理论与实际联系起来,与生活实际联系起来。选A
例2:下面是小虎同学做的长度单位换算的几个算式,请指出他在换算过程中的错误,并写出正确的算式。
(1)5.2m=5.2m×100cm=520cm
(2)6.5×106μm=6.5×106×10-6=6.5m
(3)36μm=36×1000nm=36000nm
(4)480mm=480÷1000m=0.48
点拨:进行单位换算时,正确的格式是数字不变,把相应的单位作等量代换。
(1)式中用“100cm”代换了前面的“m”,所以中间的“m”就不应该有了;(2)式中中间没写单位;(3)式是正确的;(4)式用了除法,单位换算过程中都用乘法,且确保等式前后相等。正确的算式应为:
(1)5.2m=5.2×100cm=520cm
(2)6.5×106μm=6.5×106×10-6m=6.5m
(4)480mm=480×10-3m=0.48m
题型二:能对生活中的某个过程的时间和一些物体的长度进行比较准确的估测。
例3:以下数据,最接近一间普通教室的天花板距该教室地面的高度的是( )
A.5.5m B.3.5m C.2.0m D.1.5m
答:B
例4:下列各过程经历的时间最接近1s的是( )
A.人眼睛迅速一眨 B.人心脏跳动一次
C.人正常呼吸一次 D.人打一个呵欠
点拨:本题考查你对1s的感性认识。根据生活经验(或马上就实践一下),人迅速一眨用时小于1s,而人正常呼吸一次或一个呵欠的时间大于1s。选B。
例5:“纳米”是一种长度单位,1nm=10-9m,纳米技术是以0.1—100nm这样的尺度为研究对象的前沿科学,目前我国在对纳米技术的研究方面已经跻身世界前列。1.76×109nm可能是( )
A.一个人的身高 B.物理课本的长度
C.一座山的高度 D.一个篮球场的长度
点拨:当出现的单位是不熟悉的时,一定要将它换算成我们平时所熟悉的单位——m或cm。因此本题中,1.76×109nm=1.76×109×10-9m=1.76m,可能是一个人的高度。
题型三:知道什么叫误差,知道用多次测量求平均值的方法可减小误差
例6:某同学用刻度尺测量某一物体的长度,四次测量的数据分别1.24cm,1.25cm,2.24cm,1.24cm,那么该物体的长度是 cm。
点拨:(1)同一把尺测同一物体的长度,测量结果中的准确值应该是相同的,因此要注意题目中是否出现错误的数据,若有,要注意消除后再计算平均值。2.24cm比其他三个数据大1cm,显然是测量错误或读数错误,要消除掉。(2)用多次测量结果的平均值作为被测物体物体的长度,可以减小误差。所以最后三个正确的读数求平均值,即为测量的结果,所以物体的长度为:
==1.24dm。该物体的长度为1.24dm.
题型四:会正确使用刻度尺测量物体的长度,会使用一些特殊方法测量长度
例7: 如图2,在测物体长度时,有以下几种方式,其中操作正确的是( )
例8:如图3所示物块的长度是 cm。
点拨:读数时,要注意看测量的起点线,千万不要理所当然地认为起点都是0刻度线;读数时,还要要注意写出估读位——也就是要读到分度值的下一位。物体长度是1.67cm(读数在1.65-----1.68cm之间都是可以的)。
例9:现有一卷粗细均匀的细铜丝,要求测出它的直径。试一试,并把测量步骤和方法写出来。
点拨:细铜丝的直径很小,而常用的测量工具达不到这样的准确程度,不能直接测量,只能用累积法(积多求少法)间接地测量。将细铜丝在铅笔上紧密排绕几十圈(如30圈),如图4所示,用刻度尺测出线圈的总长度为L,则细铜丝的直径。
测 量
长度的测量
时间的测量
误 差
长度的单位及换算
正确使用刻度尺
时间的单位及换算
正确使用钟表测时间
误差的产生以及减小误差的方法
测量硬币的直径 测量圆锥(或人)的高度
图
1
4、其它方法如图1。
图2
图3
图4
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
长度和时间的测量
内 容 提 要
怎样正确使用刻度尺测量物体的长度?
答:正确使用刻度尺的方法可用五个字加以概括,即“认、放、看、读、记”.
(1)认,就是认识刻度尺。
首先,观察它的零刻线是否磨损;若零刻线磨损时,不可再把它的零刻线作为测量的起点,这时可在刻度尺上任选一清晰的刻度线作为测量的起点线,为了读数的准确,通常选取整数的刻度线为起点,避免读数时出现错误。
其次,观察它的量程和分度值;分度值越小,精确程度越高,测量所能达到的精确程度就是由刻度尺的分度值决定的。
(2)放,即尺的位置应放正。刻度尺应与被测物体的边平行,即沿着被测长度;对于较厚的刻度尺,应使刻度线的一面贴近被测物体。
(3)看,即视线不能斜歪,视线应与尺面垂直。
(4)读,即读数,除读出分度值以上的准确值外,还要估读出分度值的下一位数值(估计值)。
(5)记,指记录。记录测量结果应包括测量值和单位。
有哪些方法可用来测量特殊物体的长度?
答:1、累积法:把多个相同的薄小物体叠放在一起测量,测量出它们总的厚度(宽度),再将测量结果除以被测量的物体的数量就得到一个薄物体的厚度。如:测量一枚硬币的厚度、一张纸的厚度、细铜线的直径等。
2、化曲为直法:用线与曲线完全重合,做好两端的记号,然后轻轻地把线拉直,用刻度尺量出长度,就是曲线的长度。如测量地图上某一公路的长度、边界的长度(别忘记了将测量的长度乘以比例尺)、铅笔的周长等。
3、滚轮法:可用轮子沿曲线或直线滚动,记下轮子的滚动的圈数,测出轮子的周长,用轮子周长乘以圈数就得到被测曲线或直线的长度。本方法适用于比较长的路径的测量。
什么叫误差?它跟错误有什么不同?如何减小测量误差?
答:(1)测量值跟其实值之间的差异叫误差,误差是测量中不可避免的。误差的产生是由于测量过程中受到主观或客观因素的影响造成的。
测量错误是在测量中采用了错误的方法、错误的仪器、错误的使用方法、错误的读数方法和记录方法造成的,它时可以避免而且时必须避免的。
(2)减小误差的方法有很多,我们可以通过校准测量仪器、改进出来方法、选精确度高的仪器、多次测量取平均值等,都可以减小测量误差。
长度的单位换算时要注意什么?
答:单位换算,实际上是换算单位,要注意记住各单位之间的换算关系。数字照抄,把相应的单位作等量代换。另外,单位换算过程中都用乘法,且要确保等式前后相等。如:
5.2m=5.2×100cm=520cm(红色的100cm就表示1m)
如何才能进行比较准确的估测?
答:课程标准要求培养学生的估测能力,在现实生活中,估测能力也是非常必要的。要提高估测能力,首先要借助具体事物对1m、1dm、1cm、1mm等长度形成具体的模型,头脑里对这些长度要有比较清晰的印象,二是要记住一些具体的事物的长度,如手的一拃的长度、自己的身高等,同时也可以采用身边具体事物的长度来帮助判断分析,也就是要将理论与实际联系起来。当然,平时也要注意多想一想,多比一比,测一测,都有助于提高自己的估测的准确性。
知 识 归 类
最近几年,中考题中对测量的知识的考查主要是长度的正确测量方法与读数、误差的性质及减小误差的方法、常见长度的认识、单位换算以及在其它实验探究中涉及的时间长度测量的仪器选择等。多出现在填空、选择题和实验探究题中。
题型一:主要考查对长度单位的认识以及长度单位的换算问题
例1:一名粗心的学生在测量记录中忘记记录下单位,那么在他记录的下列数据中,哪一个数据的单位是m
A.一支新铅笔的长度:0.175 B.一名同学的高度:1.64
C.一枚壹角硬币的厚度0.24 D.一本外文字典的厚度1.35
点拨:一支新铅笔的长度约为10~20cm,0.175m=17.5cm,因而A选项是正确的。B、C、D若以m为单位,显然是不符合生活常识,是错误的。 因材,在判断分析过程中,一定要将理论与实际联系起来,与生活实际联系起来。选A
例2:下面是小虎同学做的长度单位换算的几个算式,请指出他在换算过程中的错误,并写出正确的算式。
(1)5.2m=5.2m×100cm=520cm
(2)6.5×106μm=6.5×106×10-6=6.5m
(3)36μm=36×1000nm=36000nm
(4)480mm=480÷1000m=0.48
点拨:进行单位换算时,正确的格式是数字不变,把相应的单位作等量代换。
(1)式中用“100cm”代换了前面的“m”,所以中间的“m”就不应该有了;(2)式中中间没写单位;(3)式是正确的;(4)式用了除法,单位换算过程中都用乘法,且确保等式前后相等。正确的算式应为:
(1)5.2m=5.2×100cm=520cm
(2)6.5×106μm=6.5×106×10-6m=6.5m
(4)480mm=480×10-3m=0.48m
题型二:能对生活中的某个过程的时间和一些物体的长度进行比较准确的估测。
例3:以下数据,最接近一间普通教室的天花板距该教室地面的高度的是( )
A.5.5m B.3.5m C.2.0m D.1.5m
答:B
例4:下列各过程经历的时间最接近1s的是( )
A.人眼睛迅速一眨 B.人心脏跳动一次
C.人正常呼吸一次 D.人打一个呵欠
点拨:本题考查你对1s的感性认识。根据生活经验(或马上就实践一下),人迅速一眨用时小于1s,而人正常呼吸一次或一个呵欠的时间大于1s。选B。
例5:“纳米”是一种长度单位,1nm=10-9m,纳米技术是以0.1—100nm这样的尺度为研究对象的前沿科学,目前我国在对纳米技术的研究方面已经跻身世界前列。1.76×109nm可能是( )
A.一个人的身高 B.物理课本的长度
C.一座山的高度 D.一个篮球场的长度
点拨:当出现的单位是不熟悉的时,一定要将它换算成我们平时所熟悉的单位——m或cm。因此本题中,1.76×109nm=1.76×109×10-9m=1.76m,可能是一个人的高度。
题型三:知道什么叫误差,知道用多次测量求平均值的方法可减小误差
例6:某同学用刻度尺测量某一物体的长度,四次测量的数据分别1.24cm,1.25cm,2.24cm,1.24cm,那么该物体的长度是 cm。
点拨:(1)同一把尺测同一物体的长度,测量结果中的准确值应该是相同的,因此要注意题目中是否出现错误的数据,若有,要注意消除后再计算平均值。2.24cm比其他三个数据大1cm,显然是测量错误或读数错误,要消除掉。(2)用多次测量结果的平均值作为被测物体物体的长度,可以减小误差。所以最后三个正确的读数求平均值,即为测量的结果,所以物体的长度为:
==1.24dm。该物体的长度为1.24dm.
题型四:会正确使用刻度尺测量物体的长度,会使用一些特殊方法测量长度
例7: 如图2,在测物体长度时,有以下几种方式,其中操作正确的是( )
例8:如图3所示物块的长度是 cm。
点拨:读数时,要注意看测量的起点线,千万不要理所当然地认为起点都是0刻度线;读数时,还要要注意写出估读位——也就是要读到分度值的下一位。物体长度是1.67cm(读数在1.65-----1.68cm之间都是可以的)。
例9:现有一卷粗细均匀的细铜丝,要求测出它的直径。试一试,并把测量步骤和方法写出来。
点拨:细铜丝的直径很小,而常用的测量工具达不到这样的准确程度,不能直接测量,只能用累积法(积多求少法)间接地测量。将细铜丝在铅笔上紧密排绕几十圈(如30圈),如图4所示,用刻度尺测出线圈的总长度为L,则细铜丝的直径。
测 量
长度的测量
时间的测量
误 差
长度的单位及换算
正确使用刻度尺
时间的单位及换算
正确使用钟表测时间
误差的产生以及减小误差的方法
测量硬币的直径 测量圆锥(或人)的高度
图
1
4、其它方法如图1。
图2
图3
图4
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 走进物理世界
- 1 希望你喜爱物理
- 2 测量长度和时间
- 3 长度和时间测量的应用
- 4 尝试科学探究
- 第二章 声音与环境
- 1 我们怎样听见声音
- 2 我们怎样区分声音
- 3 我们怎样区分声音(续)
- 4 让声音为人类服务
- 第三章 光和眼睛
- 1 光世界巡行
- 2 探究光的反射规律
- 3 探究平面镜成像特点
- 4 探究光的折射规律
- 5 奇妙的透镜
- 6 探究凸透镜成像规律
- 7 眼睛与光学仪器
- 第四章 物质形态及其变化
- 1 从地球变暖谈起
- 2 探究汽化和液化的特点
- 3 探究熔化和凝固的特点
- 4 升华和凝华
- 5 水循环与水资源
- 第五章 我们周围的物质
- 1 物体的质量
- 2 探究物质的密度
- 3 密度的应用
- 4 认识物质的一些物理属性
- 5 点击新材料
