2017-2018学年下学期期末复习备考高一数学黄金30题(江苏版)(必修2)专题05+小题易丢分
文档属性
| 名称 | 2017-2018学年下学期期末复习备考高一数学黄金30题(江苏版)(必修2)专题05+小题易丢分 |

|
|
| 格式 | zip | ||
| 文件大小 | 476.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-30 20:30:44 | ||
图片预览



文档简介
1.已知圆锥的顶点为,母线,互相垂直,与圆锥底面所成角为,若的面积为,则该圆锥的体积为__________.
【答案】8π
【解析】分析:作出示意图,根据条件分别求出圆锥的母线,高,底面圆半径的长,代入公式计算即可.
点睛:此题为填空题的压轴题,实际上并不难,关键在于根据题意作出相应图形,利用平面几何知识求解相应线段长,代入圆锥体积公式即可.
2.已知圆锥的顶点为,母线,所成角的余弦值为,与圆锥底面所成角为45°,若的面积为,则该圆锥的侧面积为__________.
【答案】
【解析】分析:先根据三角形面积公式求出母线长,再根据母线与底面所成角得底面半径,最后根据圆锥侧面积公式求结果.
详解:因为母线,所成角的余弦值为,所以母线,所成角的正弦值为,因为的面积为,设母线长为所以,
因为与圆锥底面所成角为45°,所以底面半径为
因此圆锥的侧面积为
点睛:本题考查线面角,圆锥的侧面积,三角形面积等知识点,考查学生空间想象与运算能力
3.(2018湖南株洲高三年级质量检测)在直三棱柱中,侧棱长为,在底面中,,,则此直三棱柱的外接球的表面积为________________.
【答案】
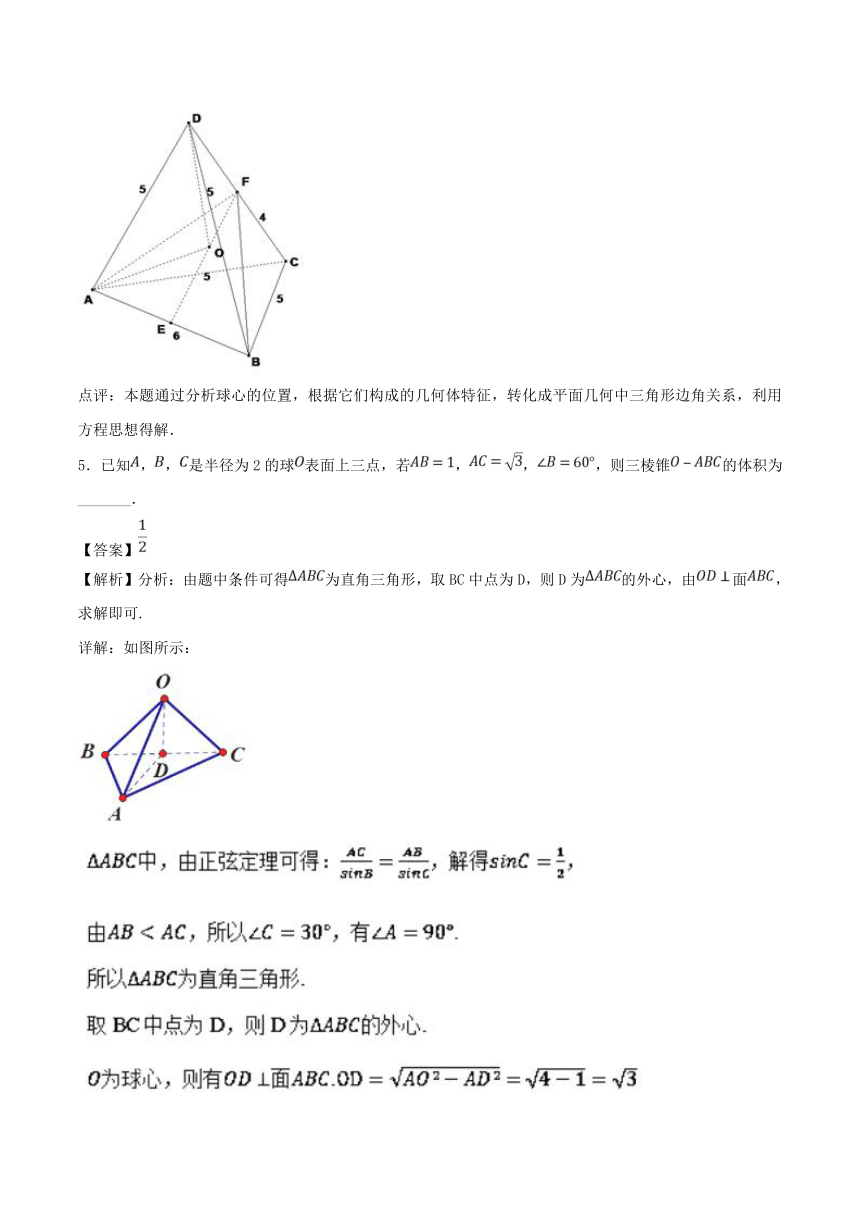
4.已知有半径分别为2、3的球各两个,且这四个球彼此相外切,现有一个球与此四个球都相外切,则此球的半径为_________________.
【答案】
【解析】思路分析:结合图形,分析四个球的球心A、B、C、D的位置,知AD=AC=BD=BC=5,AB=6,CD=4.设AB中点为E、CD中点为F,连接EF.在△ABF中可得 ,在△EBF中可得 .
由于对称性可得第五个球的球心O在EF上,连接OA、OD.设第五个球的半径为r,根据OE+OF=EF建立的方程.
如图,设四个球的球心分别为A、B、C、D,则AD=AC=BD=BC=5,AB=6,CD=4.设AB中点为E、CD中点为F,连接EF.在△ABF中求得BF=,在△EBF中求得EF=.
由于对称性可得第五个球的球心O在EF上,连接OA、OD.设第五个球的半径为r,则OA=r+3,OD=r+2,于是OE=,OF=,∵OE+OF=EF,
∴ 平方整理再平方得,解得或(舍掉),故答案为.
点评:本题通过分析球心的位置,根据它们构成的几何体特征,转化成平面几何中三角形边角关系,利用方程思想得解.
5.已知,,是半径为2的球表面上三点,若,,,则三棱锥的体积为_______.
【答案】
【解析】分析:由题中条件可得为直角三角形,取BC中点为D,则D为的外心,由面,求解即可.
详解:如图所示:
三棱锥的体积为.
故答案为:.
点睛:本题主要考查了球的内接三角形的性质,即球心和内心连线与三点所成的截面垂直,属于中档题.
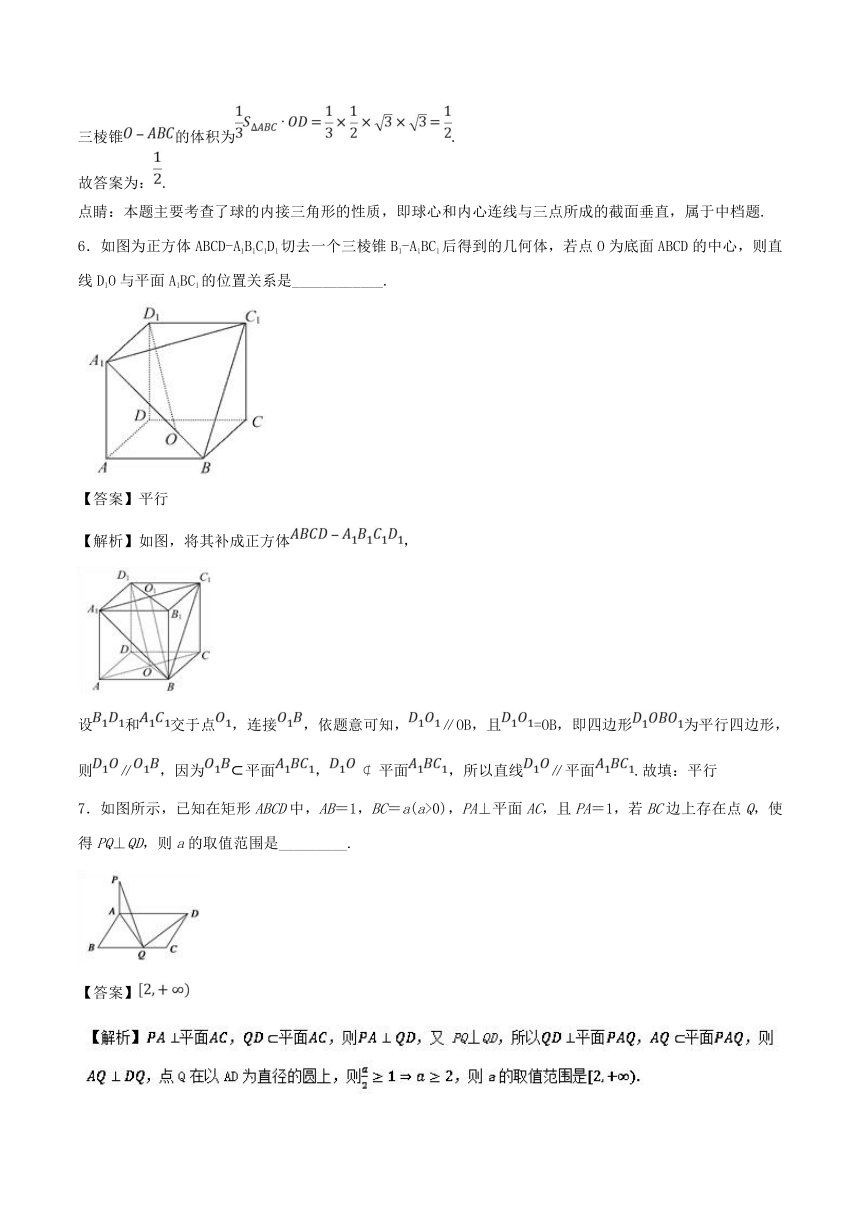
6.如图为正方体ABCD-A1B1C1D1切去一个三棱锥B1-A1BC1后得到的几何体,若点O为底面ABCD的中心,则直线D1O与平面A1BC1的位置关系是____________.
【答案】平行
【解析】如图,将其补成正方体,
设和交于点,连接,依题意可知,∥OB,且=OB,即四边形为平行四边形,则∥,因为?平面, ?平面,所以直线∥平面.故填:平行
7.如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1,若BC边上存在点Q,使得PQ⊥QD,则a的取值范围是_________.
【答案】
8.已知△ABC所在平面外一点P到△ABC三顶点的距离都相等,则点P在平面ABC内的射影是△ABC的_______.(填“重心”、“外心”、“内心”、“垂心”)
【答案】外心
【解析】过P作平面,连接,由于,则,则,点P在平面ABC内的射影是△ABC的外心.
9.已知直线, 和平面, ,且, ,则“, ”是“”的__________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”
【答案】必要不充分
10.在四棱锥中, 底面,底面是正方形, ,三棱柱的顶点都位于四棱锥的棱上,已知分别是棱的中点,则三棱柱的体积为__________.
【答案】1
【解析】由题得中点, 是DC中点, 是SC中点,PN=1,MN=,且PN⊥MN,
所以三棱柱的底面积为.
由题得正方形的对角线长,三棱柱的高为,
所以三棱柱的体积为,故填1.
点睛:本题的关键是确定、和位置,后面求三棱柱的体积就可以迎刃而解了.
11.如图,已知四边形ABCD为矩形,PA⊥平面ABCD,下列结论中正确的是________.(把正确结论的序号都填上)
①PD⊥CD;
②BD⊥平面PAO;
③PB⊥CB;
④BC∥平面PAD.
【答案】①③④
12.若α,β是两个相交平面,则在下列命题中,真命题的序号为________.(写出所有真命题的序号)
①若直线m⊥α,则在平面β内,一定不存在与直线m平行的直线;
②若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直;
③若直线m?α,则在平面β内,不一定存在与直线m垂直的直线;
④若直线m?α,则在平面β内,一定存在与直线m垂直的直线.
【答案】②④
【解析】对于①,若直线m⊥α如果α,β互相垂直,则在平面β内,存在与直线m平行的直线,故①错误;对于②,若直线m⊥α,则直线m垂直于平面α内的所有直线,在平面β内存在无数条与交线平行的直线,这无数条直线均与直线m垂直,故②正确;
对于③,④,若直线m?α,则在平面β内,一定存在与直线m垂直的直线,故③错误,④正确.
答案:②④
13.如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为________.
【答案】平行
【解析】取PD的中点F,连接EF,AF,
在△PCD中,EF綊CD.
又因为AB∥CD且CD=2AB,
所以EF綊AB,所以四边形ABEF是平行四边形,
所以EB∥AF.
又因为EB?平面PAD,AF?平面PAD,
所以BE∥平面PAD.
答案:平行
14.如图,在空间四边形ABCD中,点M∈AB,点N∈AD,若=,则直线MN与平面BDC的位置关系是________.
【答案】平行
15.已知P为△ABC所在平面外一点,且PA,PB,PC两两垂直,则下列命题:
①PA⊥BC;②PB⊥AC;③PC⊥AB;④AB⊥BC,其中正确命题的个数是________.
【答案】3
【解析】如图所示,∵PA⊥PC,PA⊥PB,PC∩PB=P,∴PA⊥平面PBC.
又∵BC?平面PBC,∴PA⊥BC.
同理PB⊥AC,PC⊥AB,但AB不一定垂直于BC.
16.实数x、y满足,则的最大值为_________.
【答案】2
【点评】本题考查了消元法及函数的最值的求法,要掌握本类试题中一些式子的几何意义,如
表示曲线上点与点(a,b)之间距离的平方;表示曲线上点与点(a,b)连线的斜率;注意将直线在坐标轴上的截距与z联系起来解题.
综上所述,解决与圆相关的最值问题的关键是要善于利用数形结合思想,利用几何知识求最值,要善于利用转化与化归思想将最值问题转化为函数的最值进行求解.一般是根据条件列出关于所求目标的式子——函数关系式,然后根据函数关系式的特征选用参数法、配方法、判别式法等,应用不等式的性质求出最值.特别地,要利用圆的几何性质,根据式子的几何意义求解,这正是数形结合思想的应用.
17.直线过点且与轴、轴分别交于两点,若恰为线段的中点,则直线的方程为_________.
【答案】3x﹣2y+12=0
【解析】设A(x,0)、B(0,y),由中点坐标公式得:
解得:x=﹣4,y=6,由直线l过点(﹣2,3)、(﹣4,0),
∴直线l的方程为:,
即3x﹣2y+12=0.
故答案为:3x﹣2y+12=0
18.已知直线l1:mx+y+4=0和直线l2:(m+2)x-ny+1=0(m,n>0)互相垂直,则的取值范围为________.
【答案】
【解析】∵直线:与直线:,.
∴,即.
∴
∵
∴,即.
故答案为.
19.过点(-1,2)且在两坐标轴上的截距相等的直线方程是________.
【答案】或
②所求的直线与两坐标轴的截距不为时,设该直线的方程为.
∵直线过点
∴
∴直线的方程为.
综上,过点且在两坐标轴上的截距相等的直线方程是或.
故答案为或.
点睛:本题主要考查直线的方程,直线的方程主要有五种形式,每种形式的直线方程都具有其局限性,斜截式与点斜式要求直线斜率存在,所以用这两种形式设直线方程时要注意讨论斜率是否存在;截距式要注意讨论截距是否为零;两点式要注意讨论直线是否与坐标轴平行;求直线方程的最终结果往往需要化为一般式.
20.在平面直角坐标系中, , ,若直线与线段有公共点,则实数的取值范围是________.
【答案】
【解析】
画出图形,如图所示,结合图象知,直线,可化为, 该直线过点
,解得,又该直线过点 ,解得,又直线与线段有公共点, 实数的取值范围是或,即实数的取值范围是
,故答案为.
21.若三条直线ax+2y+8=0,4x+3y-10=0和2x-y=0相交于一点,则实数a的值为______.
【答案】
22.直线与圆交于两点,则________.
【答案】
【解析】分析:首先将圆的一般方程转化为标准方程,得到圆心坐标和圆的半径的大小,之后应用点到直线的距离求得弦心距,借助于圆中特殊三角形半弦长、弦心距和圆的半径构成直角三角形,利用勾股定理求得弦长.
详解:根据题意,圆的方程可化为,
所以圆的圆心为,且半径是2,
根据点到直线的距离公式可以求得,
结合圆中的特殊三角形,可知,故答案为.
点睛:该题考查的是有关直线被圆截得的弦长问题,在解题的过程中,熟练应用圆中的特殊三角形半弦长、弦心距和圆的半径构成的直角三角形,借助于勾股定理求得结果.
23.(湖北省襄阳市2018届高三1月调研)已知两个不共线向量的夹角为,M、N分别为线段OA、OB的中点,点C在直线MN上,且,则的最小值为_______.
【答案】
【解析】因为三点共线,所以,
所以,,表示原点与直线上的点的距离的平方,它的最小值为,故填.
24.已知点在圆:上,点在双曲线上,则,两点之间的距离的最小值为_______________.
【答案】
25.已知直线于圆交于两点,圆在点处的切线相交于点,则四边形的面积为__________.
【答案】5
【解析】由平面几何知识,得点与圆心的连线与直线垂直,则,解得,则
,因为圆心到直线的距离为,所以,则四边形 的面积为.
26.已知垂直直线于点,若,则线段长度的最大值为_____________.
【答案】
【解析】过定点,所以在以为直径的圆上,因此线段长度的最大值为.
27.若圆C过两点,且圆心C在直线x-2y-2=0上,则圆C的标准方程为_________.
【答案】
【方法点睛】本题主要考查圆的方程和性质,属于难题.求圆的方程常见思路与方法有:①直接设出动点坐标 ,根据题意列出关于的方程即可;②根据几何意义直接找到圆心坐标和半径,写出方程;③待定系数法,可以根据题意设出圆的标准方程或一般式方程,再根据所给条件求出参数即可.本题是利用方法③解答的.
28.已知直线ax+by=1(其中a、b为非零实数)与圆x2+y2=1相交于A、B两点,O为坐标原点,且△AOB为直角三角形,则的最小值为____.
【答案】4
【易错点晴】本题主要考查直线与圆的位置关系以及利用基本不等式求最值,属于难题. 利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用或时等号能否同时成立).
29.已知圆.由直线上离圆心最近的点向圆引切线,切点为,则线段的长为__________.
【答案】
【解析】圆心到直线的距离:,
结合几何关系可得线段的长度为.
30.已知A、B、C是圆x2+y2=1上的三点,且,其中O为坐标原点,则的面积等于________.
【答案】
【解析】如图所示,由||=||=||=1知,?OACB是边长为1的菱形,且∠AOB=120°.
∴S?OACB=||||sin 120°=1×1×=.
同课章节目录
