人教版数学六下圆柱与圆锥学案(含答案)
文档属性
| 名称 | 人教版数学六下圆柱与圆锥学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 463.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-02 00:00:00 | ||
图片预览



文档简介
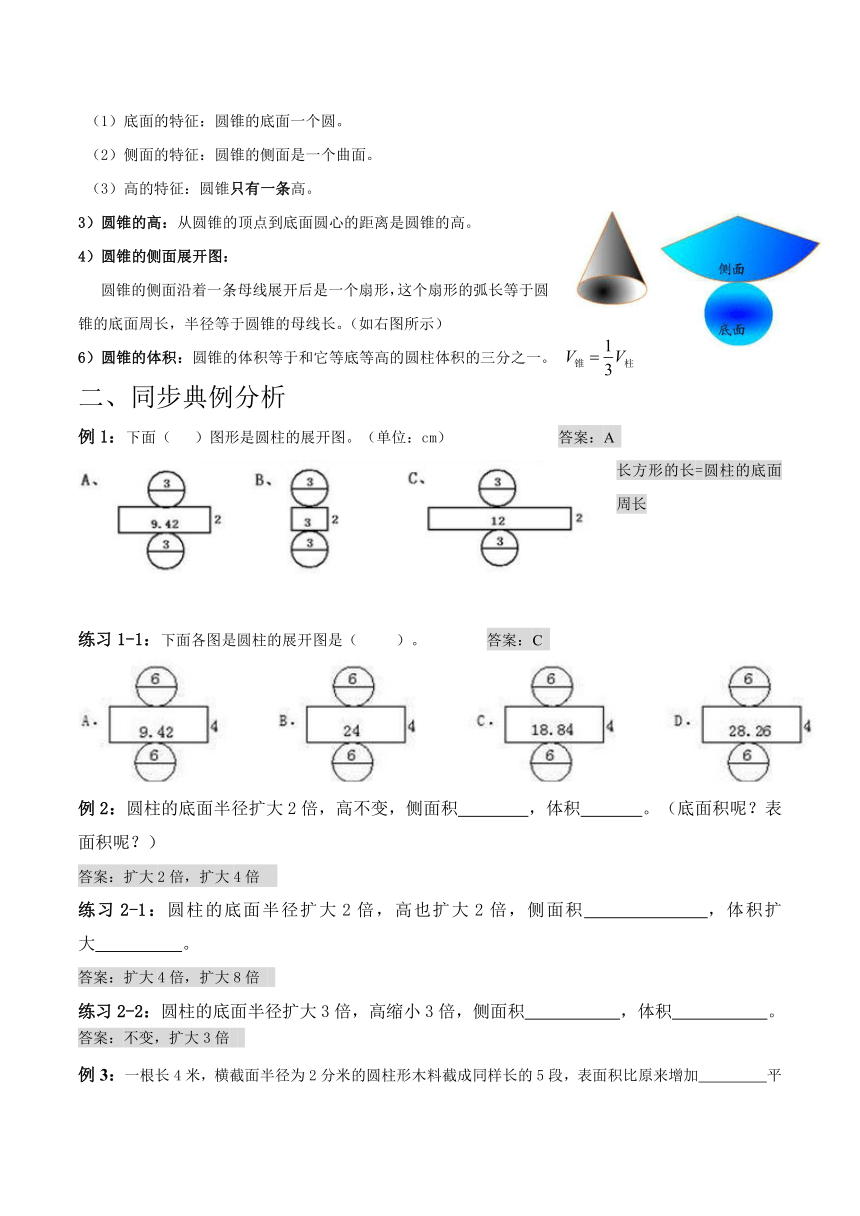
圆柱与圆锥
一、课本回顾(六年级下册P17-P39)
知识点1.圆柱
1)认识圆柱各部分的名称:
上下两个圆面叫做底面,
圆柱的周围叫侧面,
圆柱两个底面之间的距离叫做高。
2)圆柱的特征:?
(1)底面的特征:圆柱的底面是完全相等的两个圆。?
(2)侧面的特征:圆柱的侧面是一个曲面。?
(3)高的特征:圆柱有无数条高。?
3)圆柱的高:两个底面之间的距离叫做高。?
4)圆柱的侧面展开图:?
当沿高展开时展开图是(长方形);?
这个长方形的长等于(圆柱的底面周长),长方形的宽等于(圆柱的高)。这个长方形的面积等于(圆柱的侧面积),因为长方形面积=长×宽,所以圆柱的侧面积=底面周长×高?
当底面周长和高相等时,沿高展开图是(正方形);?当不沿高展开时展开图是(平行四边形)。
5)圆柱的表面积:圆柱的表面积=侧面积+底面积×2 (链接侧面积和底面面积求解公式)
6)圆柱的体积:圆柱的体积=底面积×高 字母表示:V=Sh
7)圆柱的其他知识:
(1)圆柱的横切:切成n段,需要n-1次,增加2×(n-1)个底面积 (1、2选讲)
(2)圆柱的纵切:切1次,增加2个长方形,长方形的长是底面的直径,宽是圆柱的高
(3)当侧面积一定时,越是细、长的圆柱体积越小,越是粗、矮的圆柱体积越大。
知识点2.
1)认识圆锥各部分的名称:
下面一个圆面叫做底面,
它周围叫侧面,
从圆锥的顶点到底面圆心的距离叫做高。
2)圆锥的特征:
(1)底面的特征:圆锥的底面一个圆。?
(2)侧面的特征:圆锥的侧面是一个曲面。?
(3)高的特征:圆锥只有一条高。
3)圆锥的高:从圆锥的顶点到底面圆心的距离是圆锥的高。
4)圆锥的侧面展开图:
圆锥的侧面沿着一条母线展开后是一个扇形,这个扇形的弧长等于圆锥的底面周长,半径等于圆锥的母线长。(如右图所示)
6)圆锥的体积:圆锥的体积等于和它等底等高的圆柱体积的三分之一。
二、同步典例分析
例1:下面( )图形是圆柱的展开图。(单位:cm) 答案:A
长方形的长=圆柱的底面周长
练习1-1:下面各图是圆柱的展开图是( )。 答案:C
例2:圆柱的底面半径扩大2倍,高不变,侧面积 ,体积 。(底面积呢?表面积呢?)
答案:扩大2倍,扩大4倍??
练习2-1:圆柱的底面半径扩大2倍,高也扩大2倍,侧面积 ,体积扩大 。
答案:扩大4倍,扩大8倍
练习2-2:圆柱的底面半径扩大3倍,高缩小3倍,侧面积 ,体积 。
答案:不变,扩大3倍
例3:一根长4米,横截面半径为2分米的圆柱形木料截成同样长的5段,表面积比原来增加 平方分米。
答案:100.48
练习3-1:把一根长1.5米的圆柱形钢材截成三段后,如图,表面积比原来增加9.6平方分米,这根钢材原来的体积是多少?
答案:1.5米=15分米 9.6÷4×15=36立方分米
练习3-2:把长1.2米的圆柱形钢材按1:2:3截成3段,表面积比原来增加了56平方厘米,这三段圆钢中最长的一段比最短的一段体积多多少?
练习3-3:一根长2m的圆柱形木头,截去2分米的一段小圆柱后,表面积减少了12.56平方分米,那么这根木头原来的体积是多少?
例4:用一块长6.28厘米、宽3.14厘米的铁皮做圆柱形水桶的侧面,另找一块铁皮做底。这样做成的铁桶的容积最大是多少?(不截开铁皮)
法一:将长6.28分米卷起,以宽3.14分米为高 法二:将宽3.14分米卷起,以长6.28分米为高 底面半径:6.28/3.14/2=1 底面半径:3.14/3.14/2=0.5 容积:3.14*1*1*3.14=9.8596 容积:3.14*0.5*0.5*6.28=4.9298 9.8596>4.9298 第一种方法做成的水桶容积最大
练习4-1:用一块长62.8厘米,宽47.1厘米的铁皮做圆柱形水桶的侧面,另找一块铁皮做底.这样做到成铁桶的容积最大是多少? 【精确到1厘米】
第一种: d=62.8/3.14=20cm 第二种: d=47.1/3.14=15cm
r=20/2=10cm r=15/2=7.5cm
S=10×10×3.14*47.1=14789.4cm=147.894m S=7.5*7.5×3.14*62.8=11092.05cm=110.9205m
147.894<110.9205 第一种方法做成的水桶容积最大
例5:一个盛满水的圆锥体容器高9厘米,如果将水全部倒入与它等底等高的圆柱体容器中,则水高 厘米。
答案:3
练习5-1:如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?
例6:等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是(???????)立方米,圆锥的体积是(???????)立方米.
答案:24;8
练习6-1:等底等高的一个圆柱和一个圆锥的体积和是96立方分米,圆柱的体积是(???????)立方分米,圆锥的体积是(???????)立方分米
答案:圆柱的体积是:96÷(3+1)×3=72(立方分米)
圆锥的体积是:72÷3=24(立方分米)
专题训练
题型一、表面积变化
例1:一个圆柱的高减少2厘米侧面积就减少50.24平方厘米,它的体积减少多少立方厘米?
底面周长:50.24÷2=25.12(厘米); 底面半径:25.12÷3.14÷2=4(厘米); 底面积:3.14×42=50.24(平方厘米); 减少的体积:50.24×2=100.48(立方厘米);
练习1-1:一个圆柱的高增加3分米,侧面积就增加56.52平方分米,它的体积增加多少立方分米?
底面周长是:56.52/3=18.84? 底面半径是:18.84/(3.14*2)=3? 它的体积增加:3.14*3*3*3=84.78?
例2:一个圆柱的侧面展开是一个正方形。如果高增加2厘米,表面积增加12.56平方厘米。原来这个圆柱的侧面积是多少平方厘米?
底面周长:12.56÷2=6.28厘米.底面半径:6.28÷3.14÷2=1厘米 底面积:3.14×12=3.14平方厘米 原表面积:6.28×6.28-12.56+3.14×2=26.8784+6.28=33.1584平方厘米 体积:3.14×(6.28-2)=13.4392立方厘米
练习2-1:一个圆柱的侧面展开是一个正方形。如果高减少3分米,表面积减少94.2平方分米。原来这个圆柱的体积是多少立方分米?
练习2-2:一个圆柱体的高和底面周长相等。如果高缩短2厘米,表面积就减少12.56平方厘米,求这个圆柱的表面积。
解:12.56÷2=6.28(厘米)---底面周长
侧面积:6.28*6.28=39.4384(平方厘米)
6.28÷3.14÷2=1厘米---半径
底面积:3.14*1*1=3.14(平方厘米) 表面积:39.4384+3.14*2=45.7184(平方厘米)
题型二、拼、切圆柱
例1:把一个高是6分米的圆柱,沿着底面直径竖直切开,平均分成两半,表面积增加48平方分米。原来这个圆柱的体积是多少立方分米?
练习1-1:把两个完全一样的半个圆柱合并成一个圆柱,底面半径是3厘米,表面积减少72平方厘米。现在这个圆柱的侧面积是多少平方厘米?
练习1-2:把一根圆柱形木材沿底面直径切开成两个半圆柱体,已知一个剖面的面积是960平方厘米,半圆柱的体积是3014.4立方厘米,求原来圆柱形木材的体积和侧面积。
例2:把一个长3分米的圆柱,平均分成两段圆柱,表面积增加6.28平方分米。原来这个圆柱体积是多少立方分米?
练习2-1:把3完全一样的圆柱,连接成一个大圆柱,长9厘米,表面积减少12.56平方分米。原来每个圆柱的体积是多少立方厘米?
题型三、加工圆柱
例1:一个正方体棱长是4分米,把它削成一个最大的圆柱,削去的体积是多少?
练习1-1:一个正方体棱长是20厘米,把它削成一个最大的圆柱,这个圆柱的表面积是多少平方厘米?
例2:一个长方体,长8分米,宽8分米,高12分米。把它削成一个最大的圆柱,这个圆柱的体积为多少立方分米?
练习2-1:一个长方体,长8厘米,宽6厘米,高8厘米。把它削成一个最大的圆柱,这个圆柱体积是多少立方厘米?
题型四、旋转圆锥
例1:一个直角三角形,两条直角边分别是6厘米和9厘米,沿一条直角边旋转一周后,得到一个圆锥体,求圆锥体的体积是多少?
例2:一个直角三角形的两条直角边的长分别是6厘米和8厘米,斜边长10厘米,沿斜边所在的直线旋转一周后,得到一个旋转体,旋转体的体积是多少?
沿斜边所在的直线旋转一周后,得到一 个旋转体为上下两个圆锥体,圆锥体底面半径为直角至斜边的高=2.4,上下圆锥体的高分别为3.2、1.8,之和即为斜边长. V=3.2/3*3.14*2.42+1.8/3*3.14*2.42=5/3*3.14*2.42=30.144cm2
练习2-1:一个菱形的两条对角线分别为4厘米和6厘米,以菱形的对角线为轴旋转,转成的立体图形的体积是多少?
一、课本回顾(六年级下册P17-P39)
知识点1.圆柱
1)认识圆柱各部分的名称:
上下两个圆面叫做底面,
圆柱的周围叫侧面,
圆柱两个底面之间的距离叫做高。
2)圆柱的特征:?
(1)底面的特征:圆柱的底面是完全相等的两个圆。?
(2)侧面的特征:圆柱的侧面是一个曲面。?
(3)高的特征:圆柱有无数条高。?
3)圆柱的高:两个底面之间的距离叫做高。?
4)圆柱的侧面展开图:?
当沿高展开时展开图是(长方形);?
这个长方形的长等于(圆柱的底面周长),长方形的宽等于(圆柱的高)。这个长方形的面积等于(圆柱的侧面积),因为长方形面积=长×宽,所以圆柱的侧面积=底面周长×高?
当底面周长和高相等时,沿高展开图是(正方形);?当不沿高展开时展开图是(平行四边形)。
5)圆柱的表面积:圆柱的表面积=侧面积+底面积×2 (链接侧面积和底面面积求解公式)
6)圆柱的体积:圆柱的体积=底面积×高 字母表示:V=Sh
7)圆柱的其他知识:
(1)圆柱的横切:切成n段,需要n-1次,增加2×(n-1)个底面积 (1、2选讲)
(2)圆柱的纵切:切1次,增加2个长方形,长方形的长是底面的直径,宽是圆柱的高
(3)当侧面积一定时,越是细、长的圆柱体积越小,越是粗、矮的圆柱体积越大。
知识点2.
1)认识圆锥各部分的名称:
下面一个圆面叫做底面,
它周围叫侧面,
从圆锥的顶点到底面圆心的距离叫做高。
2)圆锥的特征:
(1)底面的特征:圆锥的底面一个圆。?
(2)侧面的特征:圆锥的侧面是一个曲面。?
(3)高的特征:圆锥只有一条高。
3)圆锥的高:从圆锥的顶点到底面圆心的距离是圆锥的高。
4)圆锥的侧面展开图:
圆锥的侧面沿着一条母线展开后是一个扇形,这个扇形的弧长等于圆锥的底面周长,半径等于圆锥的母线长。(如右图所示)
6)圆锥的体积:圆锥的体积等于和它等底等高的圆柱体积的三分之一。
二、同步典例分析
例1:下面( )图形是圆柱的展开图。(单位:cm) 答案:A
长方形的长=圆柱的底面周长
练习1-1:下面各图是圆柱的展开图是( )。 答案:C
例2:圆柱的底面半径扩大2倍,高不变,侧面积 ,体积 。(底面积呢?表面积呢?)
答案:扩大2倍,扩大4倍??
练习2-1:圆柱的底面半径扩大2倍,高也扩大2倍,侧面积 ,体积扩大 。
答案:扩大4倍,扩大8倍
练习2-2:圆柱的底面半径扩大3倍,高缩小3倍,侧面积 ,体积 。
答案:不变,扩大3倍
例3:一根长4米,横截面半径为2分米的圆柱形木料截成同样长的5段,表面积比原来增加 平方分米。
答案:100.48
练习3-1:把一根长1.5米的圆柱形钢材截成三段后,如图,表面积比原来增加9.6平方分米,这根钢材原来的体积是多少?
答案:1.5米=15分米 9.6÷4×15=36立方分米
练习3-2:把长1.2米的圆柱形钢材按1:2:3截成3段,表面积比原来增加了56平方厘米,这三段圆钢中最长的一段比最短的一段体积多多少?
练习3-3:一根长2m的圆柱形木头,截去2分米的一段小圆柱后,表面积减少了12.56平方分米,那么这根木头原来的体积是多少?
例4:用一块长6.28厘米、宽3.14厘米的铁皮做圆柱形水桶的侧面,另找一块铁皮做底。这样做成的铁桶的容积最大是多少?(不截开铁皮)
法一:将长6.28分米卷起,以宽3.14分米为高 法二:将宽3.14分米卷起,以长6.28分米为高 底面半径:6.28/3.14/2=1 底面半径:3.14/3.14/2=0.5 容积:3.14*1*1*3.14=9.8596 容积:3.14*0.5*0.5*6.28=4.9298 9.8596>4.9298 第一种方法做成的水桶容积最大
练习4-1:用一块长62.8厘米,宽47.1厘米的铁皮做圆柱形水桶的侧面,另找一块铁皮做底.这样做到成铁桶的容积最大是多少? 【精确到1厘米】
第一种: d=62.8/3.14=20cm 第二种: d=47.1/3.14=15cm
r=20/2=10cm r=15/2=7.5cm
S=10×10×3.14*47.1=14789.4cm=147.894m S=7.5*7.5×3.14*62.8=11092.05cm=110.9205m
147.894<110.9205 第一种方法做成的水桶容积最大
例5:一个盛满水的圆锥体容器高9厘米,如果将水全部倒入与它等底等高的圆柱体容器中,则水高 厘米。
答案:3
练习5-1:如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?
例6:等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是(???????)立方米,圆锥的体积是(???????)立方米.
答案:24;8
练习6-1:等底等高的一个圆柱和一个圆锥的体积和是96立方分米,圆柱的体积是(???????)立方分米,圆锥的体积是(???????)立方分米
答案:圆柱的体积是:96÷(3+1)×3=72(立方分米)
圆锥的体积是:72÷3=24(立方分米)
专题训练
题型一、表面积变化
例1:一个圆柱的高减少2厘米侧面积就减少50.24平方厘米,它的体积减少多少立方厘米?
底面周长:50.24÷2=25.12(厘米); 底面半径:25.12÷3.14÷2=4(厘米); 底面积:3.14×42=50.24(平方厘米); 减少的体积:50.24×2=100.48(立方厘米);
练习1-1:一个圆柱的高增加3分米,侧面积就增加56.52平方分米,它的体积增加多少立方分米?
底面周长是:56.52/3=18.84? 底面半径是:18.84/(3.14*2)=3? 它的体积增加:3.14*3*3*3=84.78?
例2:一个圆柱的侧面展开是一个正方形。如果高增加2厘米,表面积增加12.56平方厘米。原来这个圆柱的侧面积是多少平方厘米?
底面周长:12.56÷2=6.28厘米.底面半径:6.28÷3.14÷2=1厘米 底面积:3.14×12=3.14平方厘米 原表面积:6.28×6.28-12.56+3.14×2=26.8784+6.28=33.1584平方厘米 体积:3.14×(6.28-2)=13.4392立方厘米
练习2-1:一个圆柱的侧面展开是一个正方形。如果高减少3分米,表面积减少94.2平方分米。原来这个圆柱的体积是多少立方分米?
练习2-2:一个圆柱体的高和底面周长相等。如果高缩短2厘米,表面积就减少12.56平方厘米,求这个圆柱的表面积。
解:12.56÷2=6.28(厘米)---底面周长
侧面积:6.28*6.28=39.4384(平方厘米)
6.28÷3.14÷2=1厘米---半径
底面积:3.14*1*1=3.14(平方厘米) 表面积:39.4384+3.14*2=45.7184(平方厘米)
题型二、拼、切圆柱
例1:把一个高是6分米的圆柱,沿着底面直径竖直切开,平均分成两半,表面积增加48平方分米。原来这个圆柱的体积是多少立方分米?
练习1-1:把两个完全一样的半个圆柱合并成一个圆柱,底面半径是3厘米,表面积减少72平方厘米。现在这个圆柱的侧面积是多少平方厘米?
练习1-2:把一根圆柱形木材沿底面直径切开成两个半圆柱体,已知一个剖面的面积是960平方厘米,半圆柱的体积是3014.4立方厘米,求原来圆柱形木材的体积和侧面积。
例2:把一个长3分米的圆柱,平均分成两段圆柱,表面积增加6.28平方分米。原来这个圆柱体积是多少立方分米?
练习2-1:把3完全一样的圆柱,连接成一个大圆柱,长9厘米,表面积减少12.56平方分米。原来每个圆柱的体积是多少立方厘米?
题型三、加工圆柱
例1:一个正方体棱长是4分米,把它削成一个最大的圆柱,削去的体积是多少?
练习1-1:一个正方体棱长是20厘米,把它削成一个最大的圆柱,这个圆柱的表面积是多少平方厘米?
例2:一个长方体,长8分米,宽8分米,高12分米。把它削成一个最大的圆柱,这个圆柱的体积为多少立方分米?
练习2-1:一个长方体,长8厘米,宽6厘米,高8厘米。把它削成一个最大的圆柱,这个圆柱体积是多少立方厘米?
题型四、旋转圆锥
例1:一个直角三角形,两条直角边分别是6厘米和9厘米,沿一条直角边旋转一周后,得到一个圆锥体,求圆锥体的体积是多少?
例2:一个直角三角形的两条直角边的长分别是6厘米和8厘米,斜边长10厘米,沿斜边所在的直线旋转一周后,得到一个旋转体,旋转体的体积是多少?
沿斜边所在的直线旋转一周后,得到一 个旋转体为上下两个圆锥体,圆锥体底面半径为直角至斜边的高=2.4,上下圆锥体的高分别为3.2、1.8,之和即为斜边长. V=3.2/3*3.14*2.42+1.8/3*3.14*2.42=5/3*3.14*2.42=30.144cm2
练习2-1:一个菱形的两条对角线分别为4厘米和6厘米,以菱形的对角线为轴旋转,转成的立体图形的体积是多少?
