2018年秋八年级数学上册第11章数的开方本章总结提升导学课件(新版)华东师大版
文档属性
| 名称 | 2018年秋八年级数学上册第11章数的开方本章总结提升导学课件(新版)华东师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 404.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-05 07:54:07 | ||
图片预览







文档简介
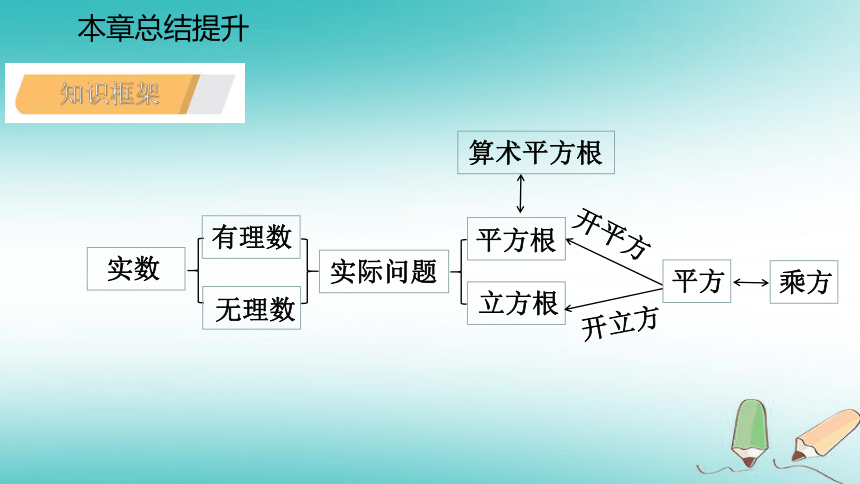
课件24张PPT。第11章 数的开方本章总结提升 本章总结提升第11章 数的开方本章总结提升知识框架实数无理数有理数立方根平方根实际问题平方开平方开立方乘方算术平方根问题一 平方根的概念及性质什么是平方根?平方根有哪些性质?如何求一个非负数的平方根?平方与开平方有什么关系?本章总结提升例1 下列说法中正确的是( )
A.-4没有平方根,也没有立方根
B.1的立方根是±1
C.(-2)2有立方根没有平方根
D.-3是9的平方根【解析】-4<0,没有平方根,但是它有立方根;1的立方根是1;(-2)2>0,它有平方根;9的平方根是3和-3,故-3是9的平方根.D本章总结提升例2 若2a-3和a-12是m的平方根,求m的值.解:由2a-3和a-12是m的平方根,
可得2a-3和a-12相等或互为相反数.
(1)当2a-3=a-12时, 解得a=-9,所以2a-3=-18-3=-21,所以m=
(-21)2=441.
(2)当(2a-3)+(a-12)=0时,解得 a=5,所以2a-3=10-3=7,所以m=72=49.
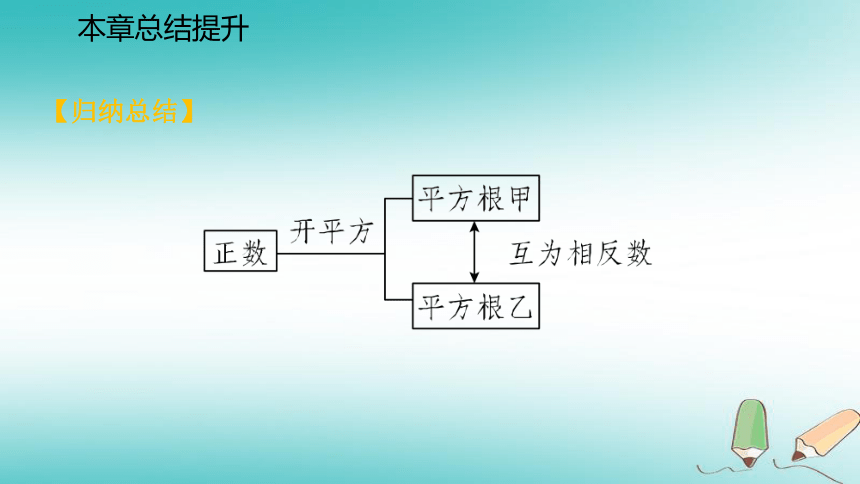
综上可知,m的值为441或49.本章总结提升【归纳总结】本章总结提升问题二 算术平方根的概念及性质C 本章总结提升什么是算术平方根?算术平方根与平方根有哪些区别和联系?如何求一个非负数的算术平方根?【归纳总结】 正数a的正的平方根就是a的算术平方根,正数a的算术平方根是a的一个平方根.一个非负数的算术平方根只有一个.本章总结提升问题三 立方根的概念及其性质什么是立方根?立方根有哪些性质?如何求一个数的立方根?立方与开立方有什么关系?本章总结提升解:∵a+3的立方根是2,∴a+3=8,解得a=5.∵3a+b-1的平方根是±6,∴3a+b-1=36,解得b=22,∴a+2b=5+2×22=49.∵49的算术平方根是7,∴a+2b的算术平方根是7.本章总结提升例4 已知a+3的立方根是2,3a+b-1的平方根是±6,则a+2b的算术平方根是多少?问题四 无理数的概念及实数的分类A本章总结提升什么叫做无理数?无理数和有理数的区别是什么?实数由哪些数组成?问题五 实数与数轴实数与数轴上的点有什么关系?本章总结提升本章总结提升问题六 实数的大小比较及运算本章总结提升数的概念是怎样从正整数逐步发展到实数的?随着数的不断扩充,数的运算有什么发展?加法和乘法的运算律始终保持不变吗?如何比较两个实数的大小呢?本章总结提升【归纳总结】 实数的大小比较有以下三种常见方法:
(1)作差法;(2)作商法;(3)取近似值法.本章总结提升专题阅读 平方根的运算典例分析
有关平方根的运算是本章的重点内容,也是本章的难点,有些同学感到不容易理解.为了帮助大家更好地掌握有关平方根的运算,本文从问题的类型、解题技巧和需要注意的方面举例说明,供大家学习时参考.
本章总结提升一 平方根定义的应用例1 若正数m的两个平方根分别是2a+3和a-12,求m的值.【解析】 根据“一个正数的平方根有两个,且它们互为相反数”来解.解: 因为一个正数的平方根有两个,且它们互为相反数,
所以(2a+3)+(a-12)=0,解得a=3,
故2a+3=2×3+3=9,a-12=3-12=-9,
从而m=(±9)2=81.【点评】 利用平方根的定义解题要深刻理解一个正数的两个平方根互为相反数,列方程求解.本章总结提升二 算术平方根性质的应用本章总结提升【点评】要挖掘题中被开方数为非负数这一隐含条件,从而确定字母的取值范围或取值本章总结提升三 利用平方根解方程例3 已知(x+y)2-4=45,求x+y的值.【解析】 将x+y看作一个整体,则(x+y)2=49,那么x+y为49的平方根,再由平方根的概念求解.解:因为(x+y)2-4=45,所以(x+y)2=49.
又因为(±7)2=49,
所以x+y=-7 或x+y=7.【点评】 将x+y看作一个整体,并理解x+y为49 的平方根.本章总结提升四 平方根的估算本章总结提升【点评】 先估算带根号的数的整数部分,根据它的整数部分,推出其小数部分,再根据它参与的算式确定算式结果的整数部分和小数部分.本章总结提升
A.-4没有平方根,也没有立方根
B.1的立方根是±1
C.(-2)2有立方根没有平方根
D.-3是9的平方根【解析】-4<0,没有平方根,但是它有立方根;1的立方根是1;(-2)2>0,它有平方根;9的平方根是3和-3,故-3是9的平方根.D本章总结提升例2 若2a-3和a-12是m的平方根,求m的值.解:由2a-3和a-12是m的平方根,
可得2a-3和a-12相等或互为相反数.
(1)当2a-3=a-12时, 解得a=-9,所以2a-3=-18-3=-21,所以m=
(-21)2=441.
(2)当(2a-3)+(a-12)=0时,解得 a=5,所以2a-3=10-3=7,所以m=72=49.
综上可知,m的值为441或49.本章总结提升【归纳总结】本章总结提升问题二 算术平方根的概念及性质C 本章总结提升什么是算术平方根?算术平方根与平方根有哪些区别和联系?如何求一个非负数的算术平方根?【归纳总结】 正数a的正的平方根就是a的算术平方根,正数a的算术平方根是a的一个平方根.一个非负数的算术平方根只有一个.本章总结提升问题三 立方根的概念及其性质什么是立方根?立方根有哪些性质?如何求一个数的立方根?立方与开立方有什么关系?本章总结提升解:∵a+3的立方根是2,∴a+3=8,解得a=5.∵3a+b-1的平方根是±6,∴3a+b-1=36,解得b=22,∴a+2b=5+2×22=49.∵49的算术平方根是7,∴a+2b的算术平方根是7.本章总结提升例4 已知a+3的立方根是2,3a+b-1的平方根是±6,则a+2b的算术平方根是多少?问题四 无理数的概念及实数的分类A本章总结提升什么叫做无理数?无理数和有理数的区别是什么?实数由哪些数组成?问题五 实数与数轴实数与数轴上的点有什么关系?本章总结提升本章总结提升问题六 实数的大小比较及运算本章总结提升数的概念是怎样从正整数逐步发展到实数的?随着数的不断扩充,数的运算有什么发展?加法和乘法的运算律始终保持不变吗?如何比较两个实数的大小呢?本章总结提升【归纳总结】 实数的大小比较有以下三种常见方法:
(1)作差法;(2)作商法;(3)取近似值法.本章总结提升专题阅读 平方根的运算典例分析
有关平方根的运算是本章的重点内容,也是本章的难点,有些同学感到不容易理解.为了帮助大家更好地掌握有关平方根的运算,本文从问题的类型、解题技巧和需要注意的方面举例说明,供大家学习时参考.
本章总结提升一 平方根定义的应用例1 若正数m的两个平方根分别是2a+3和a-12,求m的值.【解析】 根据“一个正数的平方根有两个,且它们互为相反数”来解.解: 因为一个正数的平方根有两个,且它们互为相反数,
所以(2a+3)+(a-12)=0,解得a=3,
故2a+3=2×3+3=9,a-12=3-12=-9,
从而m=(±9)2=81.【点评】 利用平方根的定义解题要深刻理解一个正数的两个平方根互为相反数,列方程求解.本章总结提升二 算术平方根性质的应用本章总结提升【点评】要挖掘题中被开方数为非负数这一隐含条件,从而确定字母的取值范围或取值本章总结提升三 利用平方根解方程例3 已知(x+y)2-4=45,求x+y的值.【解析】 将x+y看作一个整体,则(x+y)2=49,那么x+y为49的平方根,再由平方根的概念求解.解:因为(x+y)2-4=45,所以(x+y)2=49.
又因为(±7)2=49,
所以x+y=-7 或x+y=7.【点评】 将x+y看作一个整体,并理解x+y为49 的平方根.本章总结提升四 平方根的估算本章总结提升【点评】 先估算带根号的数的整数部分,根据它的整数部分,推出其小数部分,再根据它参与的算式确定算式结果的整数部分和小数部分.本章总结提升
