湖南省2017—2018学年八年级数学下册期末考试卷及参考答案
文档属性
| 名称 | 湖南省2017—2018学年八年级数学下册期末考试卷及参考答案 |  | |
| 格式 | zip | ||
| 文件大小 | 357.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-05 07:09:04 | ||
图片预览

文档简介
2018年上期八年级数学下册期末考试卷
选择题:(每小题4分,共40分)
1、在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2cm,则AC的长为( )
A、 4 cm; B、 2cm; C、 1 cm; D、 cm;
2、下列条件:①∠A+∠B=∠C;②∠A︰∠B︰∠C=1︰2︰3;③∠A=90°-∠B;
④∠A=∠B=∠C,其中能确定△ABC是直角三角形的条件有( )。
A、 1个; B、 2个; C、 3个; D、 4个;
3、下列图形中,是轴对称图形,但不是中心对称图形的是( )。
4、(1)对角线互相平分的四边形是平行四边形。(2)一组对边平行,另一组对边相等的四边形是平行四边形。(3)对角线相等的平行四边形是矩形(4)对角线互相垂直且相等的四边形是菱形。(5)对角线互相垂直平分且相等的四边形是正方形。正确的命题有( )。
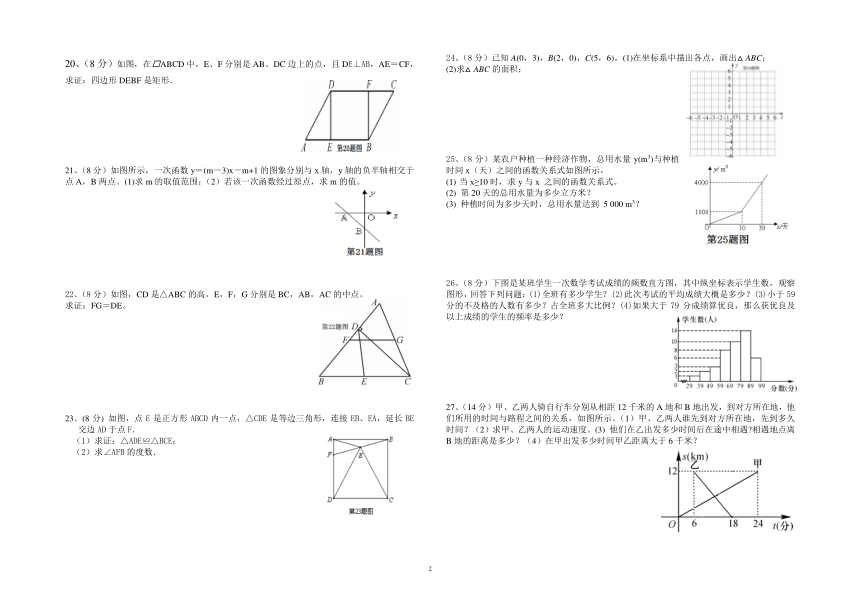
A、 2个; B、 3个; C、4个; D、 5个;
5、已知点P(m+1,2 m-3)在第四象限,则m的取值范围是( )。
A、 m <-1 B、 -<m<1 C、 -1<m< D、 m>
6、当 k+b<0, k b > 0时,一次函数 y=kx+b的图象大致是( )。
7、一水池蓄水20 m3打开阀门后每小时流出5 m3,放水后池内剩下的水的立方数 Q (m3)与放水时间t(时)的函数关系用图象表示为( )。
8、已知点P( 1 ,a ) 和Q(2,b )是一次函数y=-2x + 1的图像上的两点,则a与b的大小关系是( )。
A、a > b B、a < b C、a = b D、以上答案都不对
9、数据6,8,x,14的平均数是9,则数据8出现的频数等于( )。
A、1 B、2 C、6 D、8
10、直角三角形的三边分别为a﹣b,a,a+b 且a、b都为正整数,则三角形其中一边长可能为( ) A、61 B、71 C、81 D、91
二、填空题(每小题4分,共32分)
11、三角形三内角的度数之比为1︰2︰3,最小边的长是4cm,则另外两边的长分别是是 。
12、已知菱形的两条对角线的长分别为5cm和6cm,则它的面积是________ 。
13、已知点P1(a ,3)和P2(4,b)关于y轴对称,则的值为______ __ 。
14、如图,点A,B的坐标分别为(1,2),(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为________ 。
15、如果直线y=-2x+k的图象经过P(0,4),则它与两坐标轴所围成的三角形的面积是_____ ___。16、在全国初中数学竞赛中,永州市有40名同学进入复赛,把他们按成绩分为六组,第一组至第四组的人数分别为 10,5,7,6,第五组的频率是0.2,则第六组的频率是 ? 17、如图,将直线OA向上平移3个单位,得到一个一次函数的图象,那么这个一次函数的解析式是 。
18、如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数等
于 度。
三、解答题(共78分)。
19、(8分)某学生参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100m到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
20、(8分)如图,在□ABCD中,E、F分别是AB、DC边上的点,且DE⊥AB,AE=CF,求证:四边形DEBF是矩形.
21、(8分)如图所示,一次函数y=(m-3)x-m+1的图象分别与x轴,y轴的负半轴相交于点A,B两点。(1)求m的取值范围;(2)若该一次函数经过原点,求m的值。
22、(8分)如图,CD是△ABC的高,E,F,G分别是BC,AB,AC的中点。
求证:FG=DE。
23、(8分) 如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD于点F.
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
24、(8分)已知A(0,3),B(2,0),C(5,6)。(1)在坐标系中描出各点,画出△ABC;
(2)求△ABC的面积;
25、(8分)某农户种植一种经济作物,总用水量y(m3)与种植时间x(天)之间的函数关系式如图所示,
当x≥10时,求y与x 之间的函数关系式。
(2) 第20天的总用水量为多少立方米?
(3) 种植时间为多少天时,总用水量达到 5 000 m3?
26、(8分)下图是某班学生一次数学考试成绩的频数直方图,其中纵坐标表示学生数,观察图形,回答下列问题:(1)全班有多少学生?(2)此次考试的平均成绩大概是多少?(3)小于59分的不及格的人数有多少?占全班多大比例?(4)如果大于79分成绩算优良,那么获优良及以上成绩的学生的频率是多少?
27、(14分)甲、乙两人骑自行车分别从相距12千米的A地和B地出发,到对方所在地,他们所用的时间与路程之间的关系,如图所示。(1)甲、乙两人谁先到对方所在地,先到多久时间?(2)求甲、乙两人的运动速度。(3) 他们在乙出发多少时间后在途中相遇?相遇地点离B地的距离是多少?(4)在甲出发多少时间甲乙距离大于6千米?
2018年上期八年级数学下册期末考试卷参考答案
选择题:(每小题4分,共40分)
1、在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2cm,则AC的长为( C )
A、 4 cm; B、 2cm; C、 1 cm; D、 cm;
2、下列条件:①∠A+∠B=∠C;②∠A︰∠B︰∠C=1︰2︰3;③∠A=90°-∠B;
④∠A=∠B=∠C,其中能确定△ABC是直角三角形的条件有( D )。
A、 1个; B、 2个; C、 3个; D、 4个;
3、下列图形中,是轴对称图形,但不是中心对称图形的是( B )。
4、(1)对角线互相平分的四边形是平行四边形。(2)一组对边平行,另一组对边相等的四边形是平行四边形。(3)对角线相等的平行四边形是矩形(4)对角线互相垂直且相等的四边形是菱形。(5)对角线互相垂直平分且相等的四边形是正方形。正确的命题有( B )。
A、 2个; B、 3个; C、 4个; D、 5个;
5、已知点P(m+1,2 m-3)在第四象限,则m的取值范围是( C )。
A、 m <-1 B、 -<m<1 C、-1<m< D、 m>
6、当 k+b<0, k b > 0时,一次函数 y=kx+b的图象大致是( D )。
7、一水池蓄水20 m3打开阀门后每小时流出5 m3,放水后池内剩下的水的立方数 Q (m3)与放水时间t(时)的函数关系用图象表示为( D )。
8、已知点P( 1 ,a ) 和Q(2,b )是一次函数y=-2x + 1的图像上的两点,则a与b的大小关系是( A )。
A、a > b B、a < b C、a = b D、以上答案都不对
9、数据6,8,x,14的平均数是9,则数据8出现的频数等于( B )。
A、1 B、2 C、6 D、8
10、直角三角形的三边分别为a﹣b,a,a+b 且a、b都为正整数,则三角形其中一边长可能为( C ) A、61 B、71 C、81 D、91
二、填空题(每小题4分,共32分)
11、三角形三内角的度数之比为1︰2︰3,最小边的长是4cm,则另外两边的长分别是是 。
12、已知菱形的两条对角线的长分别为5cm和6cm,则它的面积是_____ 。
13、已知点P1(a ,3)和P2(4,b)关于y轴对称,则的值为______1 __ 。
14、如图,点A,B的坐标分别为(1,2),(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为(4,2)。
15、如果直线y=-2x+k的图象经过P(0,4),则它与两坐标轴所围成的三角形的面积是__4___。16、在全国初中数学竞赛中,永州市有40名同学进入复赛,把他们按成绩分为六组,第一组至第四组的人数分别为 10,5,7,6,第五组的频率是0.2,则第六组的频率是 0.1 。17、如图,将直线OA向上平移3个单位,得到一个一次函数的图象,那么这个一次函数的解析式是 y=2x+3 。
18、如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数等
于 175 度。
三、解答题(共78分)。
19、(8分)某学生参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100m到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
解:如图,作PC⊥AB于C,在Rt△APC中,∠APC=30°,AP=100m
∴ AC=50m 根据勾股定理得,
∵ ∠BPC=45°,∴ BC=PC=
∴ AB=AC+BC=50+=
答:A景点与景点B之间的距离为米。
20、(8分)如图,在□ABCD中,E、F分别是AB、DC边上的点,且DE⊥AB,AE=CF,求证:四边形DEBF是矩形.
证明:∵ 四边形ABCD是平行四边形
∴ CD=AB, CD∥AB,即DF∥EB
∵ AE=CF ∴ DF=EB
∴ 四边形DEBF是平行四边形
∵ DE⊥AB ∴ ∠DEB=90°
∴ 四边形DEBF是矩形.
21、(8分)如图所示,一次函数y=(m-3)x-m+1的图象分别与x轴,y轴的负半轴相交于点A,B两点。(1)求m的取值范围;(2)若该一次函数经过原点,求m的值。
解:(1)根据题意,可得解这个不等式组,得 .
因此,m的取值范围是。
(2)根据题意,得 所以 m=1
22、(8分)如图,CD是△ABC的高,E,F,G分别是BC,AB,AC的中点。
求证:FG=DE。
证明:∵ CD是△ABC的高
∴ ∠CDB=90°即△CBD是直角三角形。
∵ E 是BC的中点 ∴
∵ F,G分别是AB,AC的中点
∴ ∴ FG = DE
23、(8分) 如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD于点F.
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
(1)证明:∵ 四边形ABCD是正方形,△CDE是等边三角形,
∴ AD=DE=DC=CE=BC,∠EDC=∠ECD=60°,
∠ADC=∠BCD=∠ABC=∠BAD= 90°
∴ ∠ADE=∠ECB=30°
∴△ADE≌△BCE(SAS)
(2)解:由(1)的证明得到 △ECB是等腰三角形,∠ECB=30°
∴ ∠CEB=∠CBE =75° ∵ ∠ABC=∠BAD= 90°
∴ ∠ABC =15° ∵ ∠BAD= 90°∴ ∠AFB=75°
24、(8分)已知A(0,3),B(2,0),C(5,6)。(1)在坐标系
中描出各点,画出△ABC;(2)求△ABC的面积;
解:(1)如图。
(2)
25、(8分)某农户种植一种经济作物,总用水量y(m3)与种植时间x(天)之间的函数关系式如图所示,
当x≥10时,求y与x 之间的函数关系式.
(2) 第20天的总用水量为多少立方米?
(3) 种植时间为多少天时,总用水量达到5 000 m3?
解:(1)根据图像可设10天以上y与x的函数关系式为y=kx+b,因为图像经过点(10,1000)和点(30,4000),分别代入函数解析式得解这个方程组,得
所以,当x≥10时,y与x 之间的函数关系式是 y=150k-500
(2)当x=20时,y=150×20-500=2500,所以第20天的总用水量是2500 m3 。
(3)根据题意,得 150x-500=5000 ,解这个方程,得
答:种植时间为37天时,总用水量为5000 m3。
26、(8分)下图是某班学生一次数学考试成绩的频数直方图,其中纵坐标表示学生数,观察图形,回答下列问题:(1)全班有多少学生?(2)此次考试的平均成绩大概是多少?(3)小于59分的不及格的人数有多少?占全班多大比例?(4)如果大于79分成绩算优良,那么获优良及以上成绩的学生的频率是多少?
解:(1)1+2+3+8+10+14+6=44(人)
根据频数直方图分析,估计平均成绩在75分左右
1+2+3=6(人) 6÷44≈13.6%
(14+6)÷44≈0.45
答:(略)
27、(14分)甲、乙两人骑自行车分别从相距12千米的A地和B地出发,到对方所在地,他们所用的时间与路程之间的关系,如图所示。(1)甲、乙两人谁先到对方所在地,先到多久时间?(2)求甲、乙两人的运动速度。 (3) 他们在乙出发多少时间后在途中相遇?相遇地点离B地的距离是多少?(4)在甲出发多少时间甲乙距离大于6千米?
解:(1)根据图像观察可得,乙先到对方所在地A地,
先到24-18=6(分钟)。
(2)甲:12÷24=0.5(千米/分)
乙:12÷(18-6)=1(千米/分)
(3)根据图像,可求得甲和乙运动的函数解析式;
甲: 乙:
当时,解方程组可得
所以 12―6=6(分) 12―6=6(千米)答:在乙出发后6分钟相遇,相遇地点离B地6千米。
(4)根据题意,得 或
答: (略)
【第(3)小题另解:(12-0.5×6)÷(0.5+1)=6(分)】
选择题:(每小题4分,共40分)
1、在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2cm,则AC的长为( )
A、 4 cm; B、 2cm; C、 1 cm; D、 cm;
2、下列条件:①∠A+∠B=∠C;②∠A︰∠B︰∠C=1︰2︰3;③∠A=90°-∠B;
④∠A=∠B=∠C,其中能确定△ABC是直角三角形的条件有( )。
A、 1个; B、 2个; C、 3个; D、 4个;
3、下列图形中,是轴对称图形,但不是中心对称图形的是( )。
4、(1)对角线互相平分的四边形是平行四边形。(2)一组对边平行,另一组对边相等的四边形是平行四边形。(3)对角线相等的平行四边形是矩形(4)对角线互相垂直且相等的四边形是菱形。(5)对角线互相垂直平分且相等的四边形是正方形。正确的命题有( )。
A、 2个; B、 3个; C、4个; D、 5个;
5、已知点P(m+1,2 m-3)在第四象限,则m的取值范围是( )。
A、 m <-1 B、 -<m<1 C、 -1<m< D、 m>
6、当 k+b<0, k b > 0时,一次函数 y=kx+b的图象大致是( )。
7、一水池蓄水20 m3打开阀门后每小时流出5 m3,放水后池内剩下的水的立方数 Q (m3)与放水时间t(时)的函数关系用图象表示为( )。
8、已知点P( 1 ,a ) 和Q(2,b )是一次函数y=-2x + 1的图像上的两点,则a与b的大小关系是( )。
A、a > b B、a < b C、a = b D、以上答案都不对
9、数据6,8,x,14的平均数是9,则数据8出现的频数等于( )。
A、1 B、2 C、6 D、8
10、直角三角形的三边分别为a﹣b,a,a+b 且a、b都为正整数,则三角形其中一边长可能为( ) A、61 B、71 C、81 D、91
二、填空题(每小题4分,共32分)
11、三角形三内角的度数之比为1︰2︰3,最小边的长是4cm,则另外两边的长分别是是 。
12、已知菱形的两条对角线的长分别为5cm和6cm,则它的面积是________ 。
13、已知点P1(a ,3)和P2(4,b)关于y轴对称,则的值为______ __ 。
14、如图,点A,B的坐标分别为(1,2),(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为________ 。
15、如果直线y=-2x+k的图象经过P(0,4),则它与两坐标轴所围成的三角形的面积是_____ ___。16、在全国初中数学竞赛中,永州市有40名同学进入复赛,把他们按成绩分为六组,第一组至第四组的人数分别为 10,5,7,6,第五组的频率是0.2,则第六组的频率是 ? 17、如图,将直线OA向上平移3个单位,得到一个一次函数的图象,那么这个一次函数的解析式是 。
18、如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数等
于 度。
三、解答题(共78分)。
19、(8分)某学生参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100m到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
20、(8分)如图,在□ABCD中,E、F分别是AB、DC边上的点,且DE⊥AB,AE=CF,求证:四边形DEBF是矩形.
21、(8分)如图所示,一次函数y=(m-3)x-m+1的图象分别与x轴,y轴的负半轴相交于点A,B两点。(1)求m的取值范围;(2)若该一次函数经过原点,求m的值。
22、(8分)如图,CD是△ABC的高,E,F,G分别是BC,AB,AC的中点。
求证:FG=DE。
23、(8分) 如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD于点F.
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
24、(8分)已知A(0,3),B(2,0),C(5,6)。(1)在坐标系中描出各点,画出△ABC;
(2)求△ABC的面积;
25、(8分)某农户种植一种经济作物,总用水量y(m3)与种植时间x(天)之间的函数关系式如图所示,
当x≥10时,求y与x 之间的函数关系式。
(2) 第20天的总用水量为多少立方米?
(3) 种植时间为多少天时,总用水量达到 5 000 m3?
26、(8分)下图是某班学生一次数学考试成绩的频数直方图,其中纵坐标表示学生数,观察图形,回答下列问题:(1)全班有多少学生?(2)此次考试的平均成绩大概是多少?(3)小于59分的不及格的人数有多少?占全班多大比例?(4)如果大于79分成绩算优良,那么获优良及以上成绩的学生的频率是多少?
27、(14分)甲、乙两人骑自行车分别从相距12千米的A地和B地出发,到对方所在地,他们所用的时间与路程之间的关系,如图所示。(1)甲、乙两人谁先到对方所在地,先到多久时间?(2)求甲、乙两人的运动速度。(3) 他们在乙出发多少时间后在途中相遇?相遇地点离B地的距离是多少?(4)在甲出发多少时间甲乙距离大于6千米?
2018年上期八年级数学下册期末考试卷参考答案
选择题:(每小题4分,共40分)
1、在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2cm,则AC的长为( C )
A、 4 cm; B、 2cm; C、 1 cm; D、 cm;
2、下列条件:①∠A+∠B=∠C;②∠A︰∠B︰∠C=1︰2︰3;③∠A=90°-∠B;
④∠A=∠B=∠C,其中能确定△ABC是直角三角形的条件有( D )。
A、 1个; B、 2个; C、 3个; D、 4个;
3、下列图形中,是轴对称图形,但不是中心对称图形的是( B )。
4、(1)对角线互相平分的四边形是平行四边形。(2)一组对边平行,另一组对边相等的四边形是平行四边形。(3)对角线相等的平行四边形是矩形(4)对角线互相垂直且相等的四边形是菱形。(5)对角线互相垂直平分且相等的四边形是正方形。正确的命题有( B )。
A、 2个; B、 3个; C、 4个; D、 5个;
5、已知点P(m+1,2 m-3)在第四象限,则m的取值范围是( C )。
A、 m <-1 B、 -<m<1 C、-1<m< D、 m>
6、当 k+b<0, k b > 0时,一次函数 y=kx+b的图象大致是( D )。
7、一水池蓄水20 m3打开阀门后每小时流出5 m3,放水后池内剩下的水的立方数 Q (m3)与放水时间t(时)的函数关系用图象表示为( D )。
8、已知点P( 1 ,a ) 和Q(2,b )是一次函数y=-2x + 1的图像上的两点,则a与b的大小关系是( A )。
A、a > b B、a < b C、a = b D、以上答案都不对
9、数据6,8,x,14的平均数是9,则数据8出现的频数等于( B )。
A、1 B、2 C、6 D、8
10、直角三角形的三边分别为a﹣b,a,a+b 且a、b都为正整数,则三角形其中一边长可能为( C ) A、61 B、71 C、81 D、91
二、填空题(每小题4分,共32分)
11、三角形三内角的度数之比为1︰2︰3,最小边的长是4cm,则另外两边的长分别是是 。
12、已知菱形的两条对角线的长分别为5cm和6cm,则它的面积是_____ 。
13、已知点P1(a ,3)和P2(4,b)关于y轴对称,则的值为______1 __ 。
14、如图,点A,B的坐标分别为(1,2),(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为(4,2)。
15、如果直线y=-2x+k的图象经过P(0,4),则它与两坐标轴所围成的三角形的面积是__4___。16、在全国初中数学竞赛中,永州市有40名同学进入复赛,把他们按成绩分为六组,第一组至第四组的人数分别为 10,5,7,6,第五组的频率是0.2,则第六组的频率是 0.1 。17、如图,将直线OA向上平移3个单位,得到一个一次函数的图象,那么这个一次函数的解析式是 y=2x+3 。
18、如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数等
于 175 度。
三、解答题(共78分)。
19、(8分)某学生参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100m到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
解:如图,作PC⊥AB于C,在Rt△APC中,∠APC=30°,AP=100m
∴ AC=50m 根据勾股定理得,
∵ ∠BPC=45°,∴ BC=PC=
∴ AB=AC+BC=50+=
答:A景点与景点B之间的距离为米。
20、(8分)如图,在□ABCD中,E、F分别是AB、DC边上的点,且DE⊥AB,AE=CF,求证:四边形DEBF是矩形.
证明:∵ 四边形ABCD是平行四边形
∴ CD=AB, CD∥AB,即DF∥EB
∵ AE=CF ∴ DF=EB
∴ 四边形DEBF是平行四边形
∵ DE⊥AB ∴ ∠DEB=90°
∴ 四边形DEBF是矩形.
21、(8分)如图所示,一次函数y=(m-3)x-m+1的图象分别与x轴,y轴的负半轴相交于点A,B两点。(1)求m的取值范围;(2)若该一次函数经过原点,求m的值。
解:(1)根据题意,可得解这个不等式组,得 .
因此,m的取值范围是。
(2)根据题意,得 所以 m=1
22、(8分)如图,CD是△ABC的高,E,F,G分别是BC,AB,AC的中点。
求证:FG=DE。
证明:∵ CD是△ABC的高
∴ ∠CDB=90°即△CBD是直角三角形。
∵ E 是BC的中点 ∴
∵ F,G分别是AB,AC的中点
∴ ∴ FG = DE
23、(8分) 如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD于点F.
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
(1)证明:∵ 四边形ABCD是正方形,△CDE是等边三角形,
∴ AD=DE=DC=CE=BC,∠EDC=∠ECD=60°,
∠ADC=∠BCD=∠ABC=∠BAD= 90°
∴ ∠ADE=∠ECB=30°
∴△ADE≌△BCE(SAS)
(2)解:由(1)的证明得到 △ECB是等腰三角形,∠ECB=30°
∴ ∠CEB=∠CBE =75° ∵ ∠ABC=∠BAD= 90°
∴ ∠ABC =15° ∵ ∠BAD= 90°∴ ∠AFB=75°
24、(8分)已知A(0,3),B(2,0),C(5,6)。(1)在坐标系
中描出各点,画出△ABC;(2)求△ABC的面积;
解:(1)如图。
(2)
25、(8分)某农户种植一种经济作物,总用水量y(m3)与种植时间x(天)之间的函数关系式如图所示,
当x≥10时,求y与x 之间的函数关系式.
(2) 第20天的总用水量为多少立方米?
(3) 种植时间为多少天时,总用水量达到5 000 m3?
解:(1)根据图像可设10天以上y与x的函数关系式为y=kx+b,因为图像经过点(10,1000)和点(30,4000),分别代入函数解析式得解这个方程组,得
所以,当x≥10时,y与x 之间的函数关系式是 y=150k-500
(2)当x=20时,y=150×20-500=2500,所以第20天的总用水量是2500 m3 。
(3)根据题意,得 150x-500=5000 ,解这个方程,得
答:种植时间为37天时,总用水量为5000 m3。
26、(8分)下图是某班学生一次数学考试成绩的频数直方图,其中纵坐标表示学生数,观察图形,回答下列问题:(1)全班有多少学生?(2)此次考试的平均成绩大概是多少?(3)小于59分的不及格的人数有多少?占全班多大比例?(4)如果大于79分成绩算优良,那么获优良及以上成绩的学生的频率是多少?
解:(1)1+2+3+8+10+14+6=44(人)
根据频数直方图分析,估计平均成绩在75分左右
1+2+3=6(人) 6÷44≈13.6%
(14+6)÷44≈0.45
答:(略)
27、(14分)甲、乙两人骑自行车分别从相距12千米的A地和B地出发,到对方所在地,他们所用的时间与路程之间的关系,如图所示。(1)甲、乙两人谁先到对方所在地,先到多久时间?(2)求甲、乙两人的运动速度。 (3) 他们在乙出发多少时间后在途中相遇?相遇地点离B地的距离是多少?(4)在甲出发多少时间甲乙距离大于6千米?
解:(1)根据图像观察可得,乙先到对方所在地A地,
先到24-18=6(分钟)。
(2)甲:12÷24=0.5(千米/分)
乙:12÷(18-6)=1(千米/分)
(3)根据图像,可求得甲和乙运动的函数解析式;
甲: 乙:
当时,解方程组可得
所以 12―6=6(分) 12―6=6(千米)答:在乙出发后6分钟相遇,相遇地点离B地6千米。
(4)根据题意,得 或
答: (略)
【第(3)小题另解:(12-0.5×6)÷(0.5+1)=6(分)】
同课章节目录
