数学六年级上人教版8数学广角——数与形课件 (共19张)
文档属性
| 名称 | 数学六年级上人教版8数学广角——数与形课件 (共19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 643.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-06 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第八单元
数学广角——数与形
同学们,在生产生活中我们经常会遇到一些数学问题,仅用数(或形)来描述和表达某些事物的特征、规律等是不行的。必须把数和形结合起来进行描述和表达,才能让读者清楚地明白表达和描述的含义。下面我们就来一起研究数与形相结合的问题。
1.在生动有趣的活动中观察、寻找图形的特点,结合图形从不同的角度观察得出不同的数学规律。
2.应用“数形结合”,训练和培养数学思维能力,发散思维能力和创造性思维能力。
3.通过以形助数的直观生动性,体会数形结合,感受数学的趣味性。
知识要点1:利用正方形找规律。(重点)
从1开始,连续几个奇数的和等于奇数个数的平方。如:
知识要点2:利用画图来找规律。(难点)
某些抽象的数学加法,可以转化成图形来计算,通过画图更容易发现其中的规律。
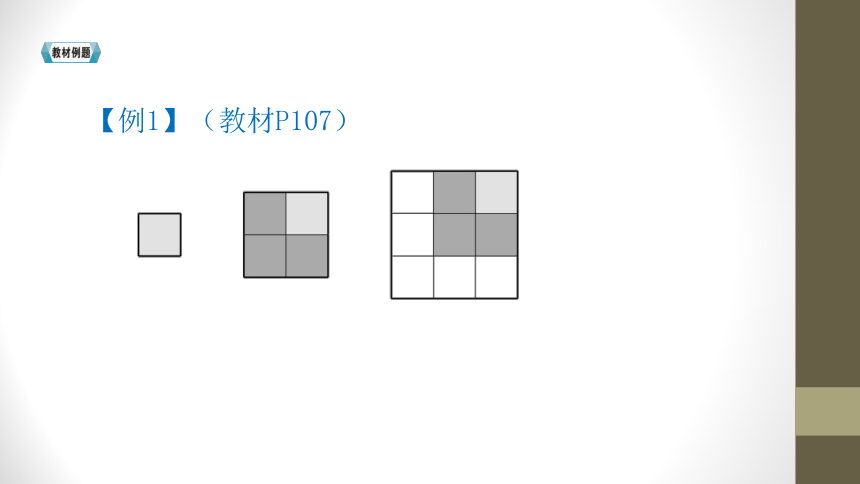
【例1】(教材P107)
(1)观察一下,上面的图和下边的算式有什么关系?把算式补充完整。
1= 1+3= 1+3+5=
(2)请你利用上面发现的规律写一写,算一算。
1+3+5+7= 1+3+5+7+9+11+13=
【解题点拨】通过计算可以发现规律。算式左边的加数是大正方形右上角的小正方形和其他“L”形图形所包含的小正方形个数之和,正好是每行或每列小正方形个数的平方。
【规范解答】
【技巧归纳】运用数形结合发现规律,即借助图形分析并观察数的运算中的规律。
☆动脑练一练
计算:1+3+5+7+…+2013+2015
提示:这个算式用一般方法计算难度很大。通过观察,各个加数是连续的奇数,可以利用例题中的数与形转化思想进行解答。
【例2】(教材P107)
计算 你能发现什么规律?
【解题点拨】(1)通过观察算式可以发现加数的规律:从第二个数开始,每个数是前一个数的1/2。
(2)规律探索。
1/2+1/4=3/4 3/4+1/8=7/8 7/8+1/16=15/16…
计算规律:题目的答案是:1-最后一个数。
一个一个加下去可以发现:计算结果越来越接近于1。
(3)画图分析:用一个圆或一条线段表示单位“1”。
从图上可以看出,这些分数不断加下去,总和就是1。
【规范解答】
【技巧归纳】(1)有些问题利用画图的方法解决起来更简单。从上图中可以直观地看出随着加数的不断增加,圆的面积和线段的长度越来越接近1,当有无限多项相加时其结果为1。(2)数形结合的方法确实是一种很好的数学方法,它能帮助我们把复杂的问题简单化,把抽象的问题直观化、形象化。
☆动脑练一练
按规律继续写下去,试试看。
【例3】停车场上有两轮摩托车和小轿车共18辆,一共有56个轮子。两轮摩托车和小轿车各有多少辆
【解题点拨】“鸡兔同笼”问题是我国古代著名的数学趣题,它在生产、生活中有着十分广泛的应用。本题就是一道“鸡兔同笼”的数学问题,题中的“两轮摩托车”相当于“鸡”,“小轿车”相当于“兔”,怎样运用“鸡兔同
笼”的解题策略求出两轮摩托车和小轿车的辆数呢
一是列表法。根据题中提供的数据,按顺序列表分析:
从表中可以看出,当两轮摩托车有8辆,小轿车有10辆时,车轮刚好是56个,符合题意。
二是假设法。假设停车场停的都是两轮摩托车,则有轮子18×2=36(个),与题中56个轮子相比较,少了20个轮子。一辆小轿车比一辆两轮摩托车多2个轮子,所以小轿车有20÷2=10(辆),由此求出摩托车有8辆。假设停车场停的都是小轿车,又应该怎样分析 怎样推算呢 请同学们想一想,试一试。
三是方程法。设两轮摩托车有x辆,则小轿车有(18-x)辆。根据“两轮摩托车的车轮数+小轿车的车轮数=车轮总数”列出方程,从而求出两轮摩托车和小轿车的辆数。
【规范解答】
设两轮摩托车有x辆,
则小轿车有(18-x)辆。
2x+4(18-x)=56
2x+72-4x=56
2x=16
x=8
18-8=10(辆)
答:两轮摩托车有8辆,小轿车有10辆。
【技巧归纳】解决“鸡兔同笼”问题的方法有很多,如列表法、假设法、方程法等,同学们可以选择自己喜欢的方法去做。如果是用方程来解决这个问题,那么一般设其中的一种动物有x只,另一种动物有(总只数-x)只,再根据脚的数量列方程求解。
☆动脑练一练
长江小学举行环保知识竞赛,一共有20道题。比赛规则是每答对一道题得5分,不答不扣分,答错一道题倒扣3分。赵放回答了所有题目,结果得了84分。他答对了多少道题?
第八单元
数学广角——数与形
同学们,在生产生活中我们经常会遇到一些数学问题,仅用数(或形)来描述和表达某些事物的特征、规律等是不行的。必须把数和形结合起来进行描述和表达,才能让读者清楚地明白表达和描述的含义。下面我们就来一起研究数与形相结合的问题。
1.在生动有趣的活动中观察、寻找图形的特点,结合图形从不同的角度观察得出不同的数学规律。
2.应用“数形结合”,训练和培养数学思维能力,发散思维能力和创造性思维能力。
3.通过以形助数的直观生动性,体会数形结合,感受数学的趣味性。
知识要点1:利用正方形找规律。(重点)
从1开始,连续几个奇数的和等于奇数个数的平方。如:
知识要点2:利用画图来找规律。(难点)
某些抽象的数学加法,可以转化成图形来计算,通过画图更容易发现其中的规律。
【例1】(教材P107)
(1)观察一下,上面的图和下边的算式有什么关系?把算式补充完整。
1= 1+3= 1+3+5=
(2)请你利用上面发现的规律写一写,算一算。
1+3+5+7= 1+3+5+7+9+11+13=
【解题点拨】通过计算可以发现规律。算式左边的加数是大正方形右上角的小正方形和其他“L”形图形所包含的小正方形个数之和,正好是每行或每列小正方形个数的平方。
【规范解答】
【技巧归纳】运用数形结合发现规律,即借助图形分析并观察数的运算中的规律。
☆动脑练一练
计算:1+3+5+7+…+2013+2015
提示:这个算式用一般方法计算难度很大。通过观察,各个加数是连续的奇数,可以利用例题中的数与形转化思想进行解答。
【例2】(教材P107)
计算 你能发现什么规律?
【解题点拨】(1)通过观察算式可以发现加数的规律:从第二个数开始,每个数是前一个数的1/2。
(2)规律探索。
1/2+1/4=3/4 3/4+1/8=7/8 7/8+1/16=15/16…
计算规律:题目的答案是:1-最后一个数。
一个一个加下去可以发现:计算结果越来越接近于1。
(3)画图分析:用一个圆或一条线段表示单位“1”。
从图上可以看出,这些分数不断加下去,总和就是1。
【规范解答】
【技巧归纳】(1)有些问题利用画图的方法解决起来更简单。从上图中可以直观地看出随着加数的不断增加,圆的面积和线段的长度越来越接近1,当有无限多项相加时其结果为1。(2)数形结合的方法确实是一种很好的数学方法,它能帮助我们把复杂的问题简单化,把抽象的问题直观化、形象化。
☆动脑练一练
按规律继续写下去,试试看。
【例3】停车场上有两轮摩托车和小轿车共18辆,一共有56个轮子。两轮摩托车和小轿车各有多少辆
【解题点拨】“鸡兔同笼”问题是我国古代著名的数学趣题,它在生产、生活中有着十分广泛的应用。本题就是一道“鸡兔同笼”的数学问题,题中的“两轮摩托车”相当于“鸡”,“小轿车”相当于“兔”,怎样运用“鸡兔同
笼”的解题策略求出两轮摩托车和小轿车的辆数呢
一是列表法。根据题中提供的数据,按顺序列表分析:
从表中可以看出,当两轮摩托车有8辆,小轿车有10辆时,车轮刚好是56个,符合题意。
二是假设法。假设停车场停的都是两轮摩托车,则有轮子18×2=36(个),与题中56个轮子相比较,少了20个轮子。一辆小轿车比一辆两轮摩托车多2个轮子,所以小轿车有20÷2=10(辆),由此求出摩托车有8辆。假设停车场停的都是小轿车,又应该怎样分析 怎样推算呢 请同学们想一想,试一试。
三是方程法。设两轮摩托车有x辆,则小轿车有(18-x)辆。根据“两轮摩托车的车轮数+小轿车的车轮数=车轮总数”列出方程,从而求出两轮摩托车和小轿车的辆数。
【规范解答】
设两轮摩托车有x辆,
则小轿车有(18-x)辆。
2x+4(18-x)=56
2x+72-4x=56
2x=16
x=8
18-8=10(辆)
答:两轮摩托车有8辆,小轿车有10辆。
【技巧归纳】解决“鸡兔同笼”问题的方法有很多,如列表法、假设法、方程法等,同学们可以选择自己喜欢的方法去做。如果是用方程来解决这个问题,那么一般设其中的一种动物有x只,另一种动物有(总只数-x)只,再根据脚的数量列方程求解。
☆动脑练一练
长江小学举行环保知识竞赛,一共有20道题。比赛规则是每答对一道题得5分,不答不扣分,答错一道题倒扣3分。赵放回答了所有题目,结果得了84分。他答对了多少道题?
