1.2 展开与折叠同步作业

21世纪教育网 –中小学教育资源及组卷应用平台
1.2 展开与折叠同步作业
姓名：__________班级：__________考号：__________
一、选择题
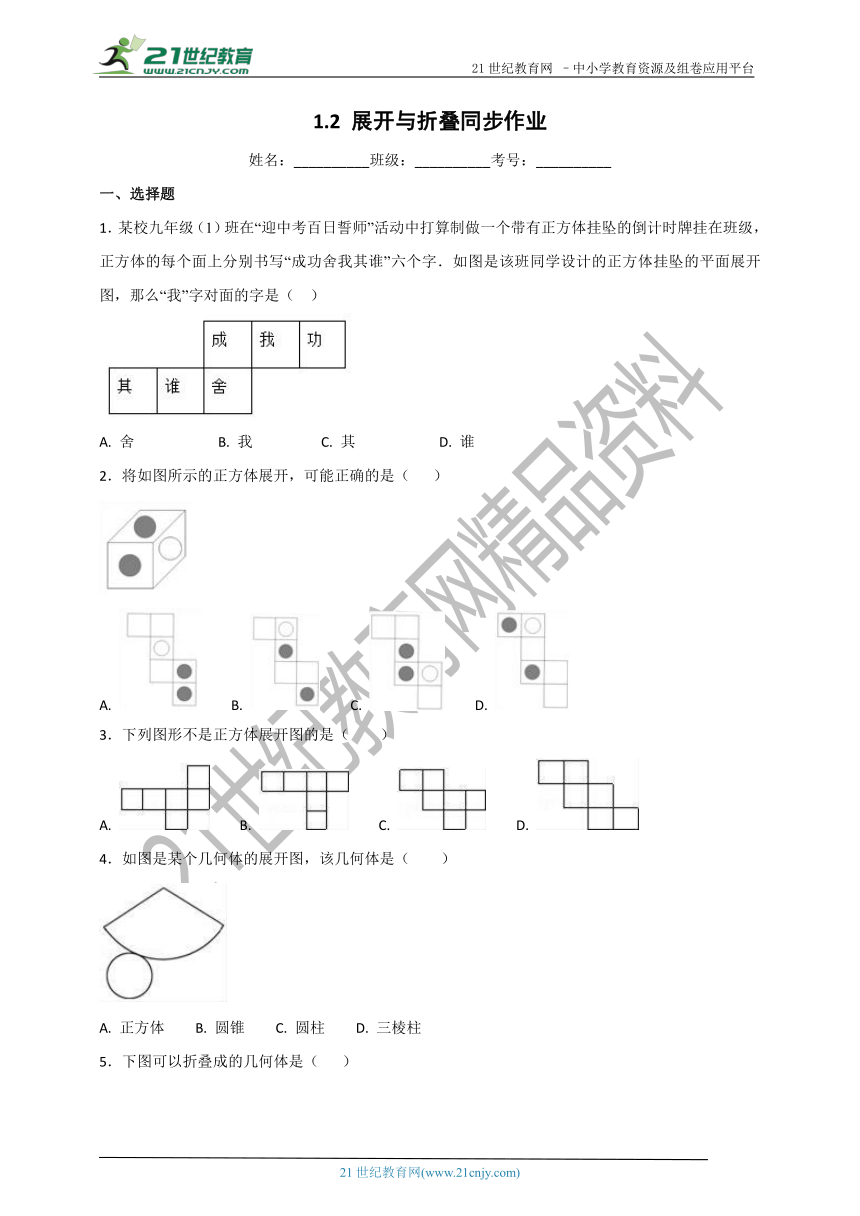
1．某校九年级（1）班在“迎中考百日誓师”活动中打算制做一个带有正方体挂坠的倒计时牌挂在班级，正方体的每个面上分别书写“成功舍我其谁”六个字．如图是该班同学设计的正方体挂坠的平面展开图，那么“我”字对面的字是（ ）
A. 舍 B. 我 C. 其 D. 谁
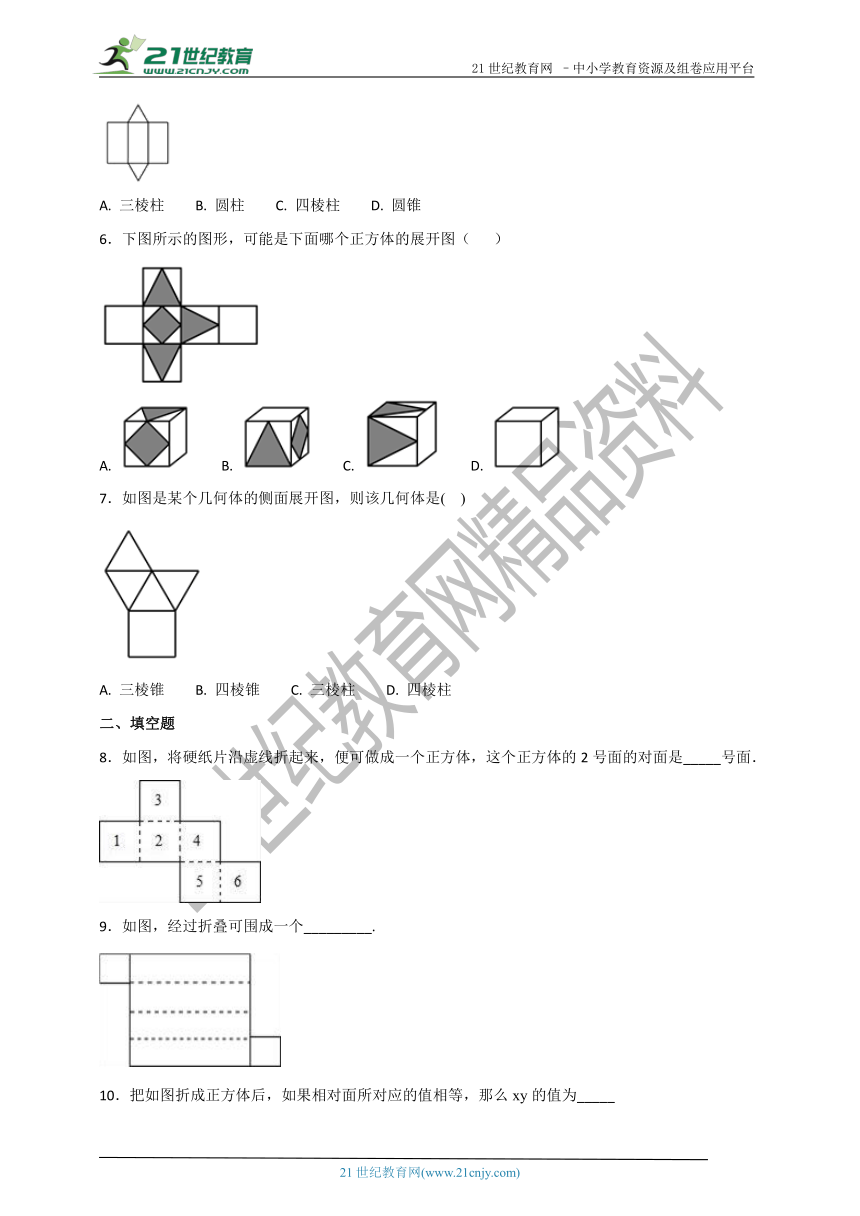
2．将如图所示的正方体展开，可能正确的是（ ）
A. B. C. D.
3．下列图形不是正方体展开图的是（　　）
A. B. C. D.
4．如图是某个几何体的展开图，该几何体是（　　）
A. 正方体 B. 圆锥 C. 圆柱 D. 三棱柱
5．下图可以折叠成的几何体是（ ）
A. 三棱柱 B. 圆柱 C. 四棱柱 D. 圆锥
6．下图所示的图形，可能是下面哪个正方体的展开图（ ）
A. B. C. D.
7．如图是某个几何体的侧面展开图，则该几何体是( )
A. 三棱锥 B. 四棱锥 C. 三棱柱 D. 四棱柱
二、填空题
8．如图，将硬纸片沿虚线折起来，便可做成一个正方体，这个正方体的2号面的对面是_____号面．
9．如图，经过折叠可围成一个_________.
10．把如图折成正方体后，如果相对面所对应的值相等，那么xy的值为_____
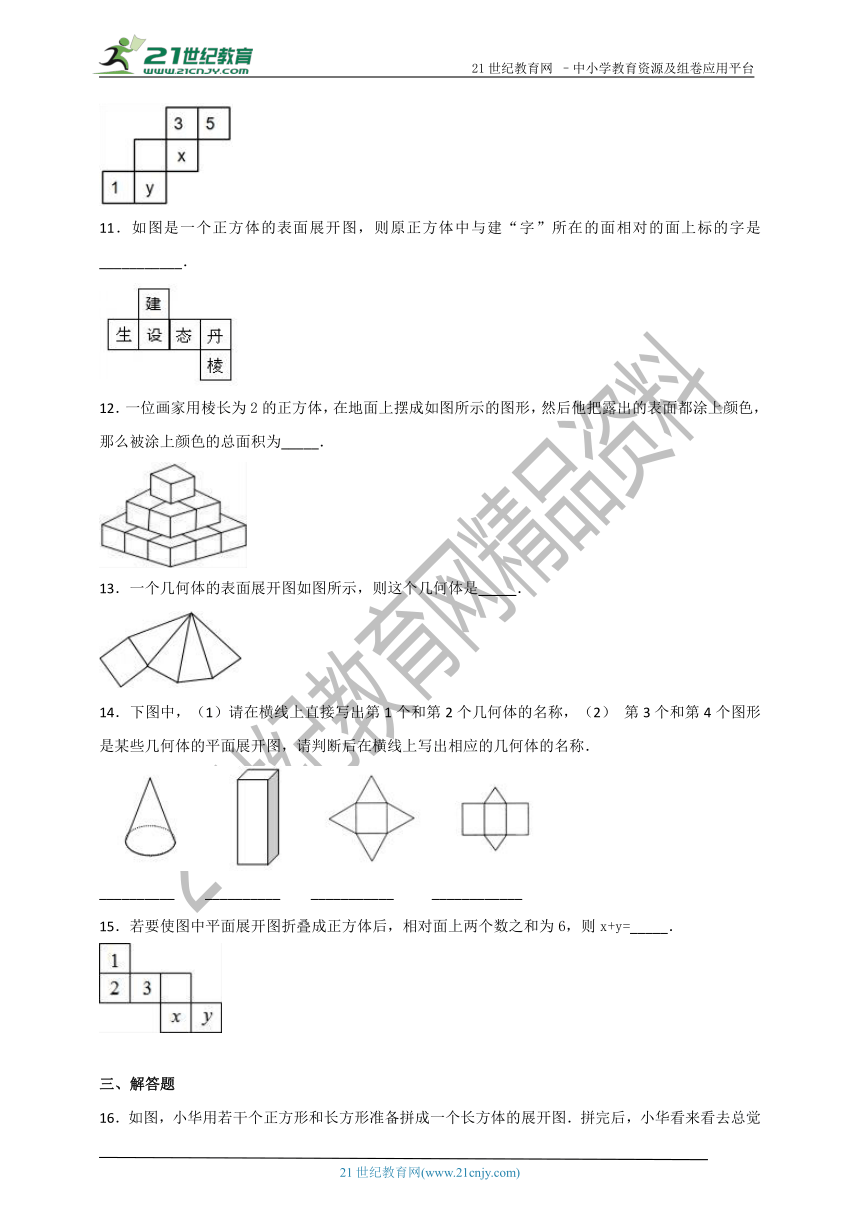
11．如图是一个正方体的表面展开图，则原正方体中与建“字”所在的面相对的面上标的字是___________．
12．一位画家用棱长为2的正方体，在地面上摆成如图所示的图形，然后他把露出的表面都涂上颜色，那么被涂上颜色的总面积为_____．
13．一个几何体的表面展开图如图所示，则这个几何体是 ．
14．下图中，（1）请在横线上直接写出第1个和第2个几何体的名称，（2） 第3个和第4个图形是某些几何体的平面展开图，请判断后在横线上写出相应的几何体的名称．
__________ __________ ___________ ____________
15．若要使图中平面展开图折叠成正方体后，相对面上两个数之和为6，则x+y=_____．
三、解答题
16．如图，小华用若干个正方形和长方形准备拼成一个长方体的展开图．拼完后，小华看来看去总觉得所拼图形似乎存在问题．
（1）请你帮小华分析一下拼图是否存在问题：若有多余块，则把图中多余部分涂黑；若还缺少，则直接在原图中补全；
（2）若图中的正方形边长为3 cm，长方形的长为5 cm，宽为3 cm，请直接写出修正后所折叠而成的长方体的体积是 cm3．
17．某长方体包装盒的表面积为146cm2，其展开图如图所示．求这个包装盒的体积．
18．如图所示,几何体是由9个小正方体堆积而成的,其中每个正方体的棱长都是1cm,画出它的三视图并求这个立体图形的表面积.
19．如图1，一个棱长为1cm的正方体按某种方式展开后，恰好能放在一个长方形内.
（1）计算：图1长方形的面积S＝_____________；
（2）小明认为把该正方体按某种方式展开后可以放在如图2所示的长方形内，请你在图2中画出这个正方体的平面展开图.
20．如图所示的立方体的六个面分别标着连续的整数，求这六个整数的和．
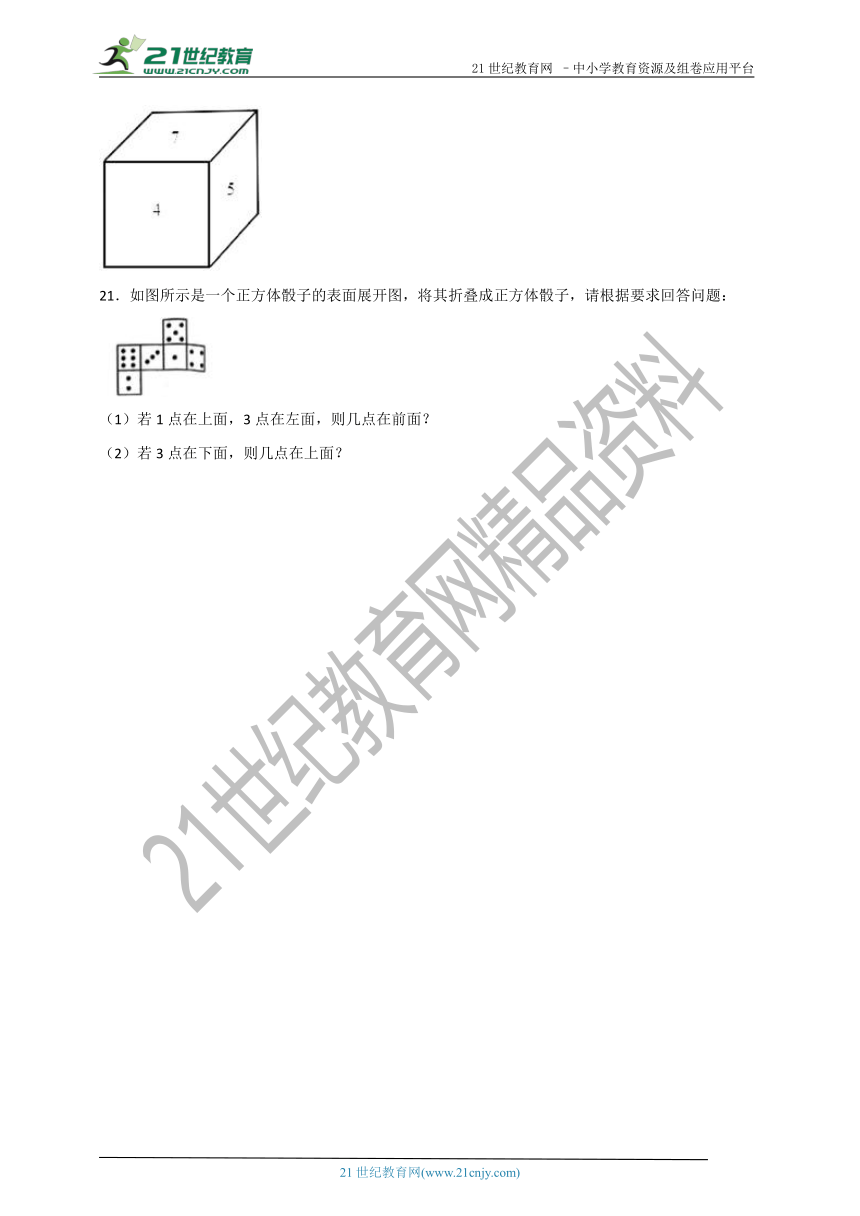
21．如图所示是一个正方体骰子的表面展开图，将其折叠成正方体骰子，请根据要求回答问题：
（1）若1点在上面，3点在左面，则几点在前面？
（2）若3点在下面，则几点在上面？
参考答案
1．D
【解析】【分析】把展开图折回立方体，便可知.
【详解】把展开图折回立方体，可知“我”字对面是“谁”字.
故选：D
【点睛】本题考核知识点：展开图. 解题关键点：把展开图折回正方体.
2．C
【解析】【分析】根据正方体的展开图，逐个折叠，再与已知图形对比，就轻易得出结果.
【详解】A.B.C.D.各个展开图逐个折叠，只有C跟已知图形相同，所以只有C正确.
故正确选项为:C.
【点睛】本题考核知识点：正方体展开图.解题关键：将展开图折叠回正方体，再进行比对.
3．B
【解析】【分析】根据平面图形的折叠及正方体的展开图进行解答即可．
【详解】A、经过折叠能围成正方体，符合正方体的展开图；
B、折叠后上边没有面，不能折成正方体，故不符合正方体的展开图；
C、经过折叠能围成正方体，符合正方体的展开图；
D、经过折叠能围成正方体，符合正方体的展开图，
故选B．
【点睛】本题主要考查了正方体展开图，熟记11个展开图，以及不是正方体展开图的常见的“一线不过四，田凹应弃之的”的图形是解题的关键．
4．B
【解析】分析：
详解：因为圆锥的展开图为一个扇形和一个圆形，故这个几何体是圆锥，
故选：B．
点睛：本题考查立体图形的平面展开图.掌握平面图形与立体图形的关系，并熟知常见几何体的平面展开图是解题的关键.
5．A
【解析】分析：根据选项中的四个图形的平面展开图即可得出答案.
详解：三棱柱的平面展开图侧面是三个等高的矩形，上下两个面是全等的三角形，与题中所示的平面展开图相符.
故选A.
点睛：本题考查立体图形的平面展开图.掌握平面图形与立体图形的关系，并熟知常见几何体的平面展开图是解题的关键.
6．C
【解析】分析：
根据展开图中四个面上的图案结合各选项能够看见的面上的图案进行分析判断即可.
详解：
A、因为A选项中的几何体展开后，阴影正方形的顶点不在阴影三角形的边上，与展开图不一致，故不可能是A；
B、因为B选项中的几何体展开后，阴影正方形的顶点不在阴影三角形的边上，与展开图不一致，故不可能是B；
C、因为C选项中的几何体展开后有可能得到如图所示的展开图，所以可能是C；
D、因为D选项中的几何体能够看见的三个面上都没有阴影图案，而展开图中有四个面上有阴影图案，所以不可能是D.
故选C.
点睛：（1）根据展开图可知，几何体的六个面中有四个面上有阴影图案；（2）展开后的图形中，阴影正方形的顶点应该在阴影三角形的边上.
7．B
【解析】分析：侧面为四个三角形，底边为四边形，故原几何体为四棱锥．
详解：观察图形可知，这个几何体是四棱锥．
故选B．
点睛：本题考查的是四棱锥的展开图，考法较新颖，需要对四棱锥有充分的理解．
8．6
【解析】这是一个正方体的平面展开图，共有六个面，其中面“1”与面“4”相对，面“3”与面“5”相对，“2”与面“6”相对．故填6．
9．长方体.
【解析】试题解析：如图，经过折叠可以围成一个长方体．
10．3
【解析】正方体的表面展开图，相对的面之间一定相隔一个正方形，
“x”与“1”是相对面，
“y”与“3”是相对面，
“5”与“空白空格”是相对面，
∵相对面所对应的值相等，
∴x=1,y=3,
∴xy=3.
故答案是:3.
11．棱
【解析】分析：正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．
详解：正方体的表面展开图中，相对的面一定隔着一个正方形.
“设”与“丹”是相对面，
“生”与“态”是相对面，
“建”与“棱”是相对面。
故答案为：棱.
点睛：考查正方体的表面展开图，熟记正方体表面展开图的特点是解题的关键.
12．132
【解析】分析：涂上颜色的总面积为：从上面看到的面积+四个侧面看到的面积．
详解：根据分析其表面积=4×（1+2+3）+9=33，即涂上颜色的为33个．
33×4=132
故答案为132．
点睛：本题考查几何体的表面积，本题的难点在于理解露出的表面的算法．
13．四棱锥．
【解析】试题分析：根据四棱锥的侧面展开图得出答案．
解：如图所示：这个几何体是四棱锥；
故答案为：四棱锥．
考点：几何体的展开图．
14．圆锥、长方体、四棱锥、三棱柱
【解析】由题意得，
圆锥、长方体、四棱锥、三棱柱.
15．8
【解析】正方体的表面展开图，相对的面之间一定相隔一个正方形，
∴1与x是相对面，3与y是相对面，
∵相对面上两个数之和为6，
∴x=5，y=3，
∴x+y=5+3=8．
故答案为：8．
16．(1)见解析；（2）45.
【解析】试题分析：(1)由于长方体有6个面,且相对的两个面全等,所以展开图是6个长方形(包括正方形),而图中所拼图形共有7个面,所以有多余块,应该去掉一个;又所拼图形中有3个全等的正方形,结合平面图形的折叠可知,可将第二行最左边的一个正方形去掉;
(2)由题意可知,此长方体的长、宽、高可分别看作3厘米、2厘米和2厘米,将数据代入长方体的体积公式即可求解.
解:(1)拼图存在问题,如图:
(2)折叠而成的长方体的体积为:3×5×3=45（cm3）.
17．这个包装盒的体积为90cm3
【解析】试题分析：设这种长方体包装盒的高为x cm，则长为（13－2x）cm，宽为 EMBED Equation.DSMT4 （14－2x）cm．根据长方体表面公式，即可列出方程，求解即可．
解：设高为x cm，则长为（13－2x）cm，宽为（14－2x）cm．由题意，得，
[（13－2x）（14－2x）+（14－2x）x＋x（13－2x）]×2＝146，
解得：x1＝2，x2＝－9（舍去）.
∴长为：9cm，宽为：5cm．长方体的体积为：9×5×2=90cm3．
答：这个包装盒的体积为90cm3．
点睛：本题主要涉及立体图形的平面展开图、立体图形的表面积、体积.解题的关键是设高为xcm，利用长方体表面积公式建立方程.
18．30平方厘米.
【解析】求这个几何体的表面积，就要数出这个图形中小正方体漏在外面的个数，从前、后、左、右、上、下等方向上来查数，然后用一个面的面积乘面的个数即可；
解：（1）从前、后、左、右、上、下方向，看到的面的个数分别为：5、5、4、4、6、6．
表面积是：1×1×（5+5+4+4+6+6）=1×30=30（cm2）.
19．（1）12cm2 ；（2）图形见解析
【解析】试题分析：
（1）根据图形结合正方体的棱长即可求解；
（2）只能有两层，所以应该是“三三”类的展开图.
试题解析：
（1）因为正方体的棱长是1，所以长方形的面积为3×4=12cm2.
（2）如图所示：
20．27或33或39．
【解析】试题分析：由平面图形的折叠及立体图形的表面展开图的特点解题，根据题意分析可得：六个面上分别写着六个连续的整数，故六个整数可能为2、3、4、5、6、7或3、4、5、6、7、8或4、5、6、7、8、9；
然后分析符合题意的一组数即可．
试题解析：∵已知三个面上的数字为4、5、7，且六个面分别标着连续的整数，
∴这六个数中一定含有4、5、6、7，
∴这六个数字可能为2、3、4、5、6、7；或3、4、5、6、7、8；或4、5、6、7、8、9；
当这六个数为2、3、4、5、6、7时，其和为2+3+4+5+6+7=27；
当这六个数为3、4、5、6、7、8时，其和为3+4+5+6+7+8=33；
当这六个数为4、5、6、7、8、9时，其和为4+5+6+7+8+9=39；
故答案为：27或33或39．
21．（1）2点在前面（2）4点在上面
【解析】试题分析：三视图问题需要空间想象能力或者就亲手做一个立方体.
试题解析：
（1）若1点在上面，3点在左面，则2点在前面.
（2）若3点在下面，则4点在上面.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)