5.6直线和圆的位置关系知识点例题
图片预览

文档简介
《直线和圆的位置关系》知识点例题
重难点典例剖析
1.直线和圆的位置关系
(1)直线和圆相交、相切、相离的概念
①相交:直线和圆有两个公共点时,直线和圆相交,这条直线叫做圆的割线.
②相切:直线和圆只有一个公共点时,直线和圆相切,这条直线叫做圆的切线,这个公共点叫做切点;
③相离:直线和圆没有公共点时,直线和圆相离.
(2)直线和圆的位置关系
如图,设r是⊙O的半径,d是圆心O到直线l的距离,则:
①直线l和⊙O相交 d②直线l和⊙O相切 d=r;
③直线l和⊙O相离 d>r;
重点突破
(1)通过直线和圆的交点的个数来定义直线和圆的三种位置关系是一种定性的描述,比较易懂.
(2)通过比较圆心到直线的距离与半径的大小来说明直线和圆的关系是一种定量的描述,这种描述使得数与形的统一,应用更加广泛.
例题
1.已知⊙O的半径为的3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( ).
A.相交 B.相切 C.相离 D.不等确定
答案:A.
解析:因为2<3,即圆心O到直线l的距离小于⊙O的半径,所以直线l与⊙O相交,故答案选A.
2.在△ABC中,∠A=90°,AB=3 cm,AC=4 cm,若以点A为圆心,3 cm长为半径作⊙A,则BC与⊙A的位置关系是( ).
A.相交 B.相切 C.相离 D.不等确定
答案:A.
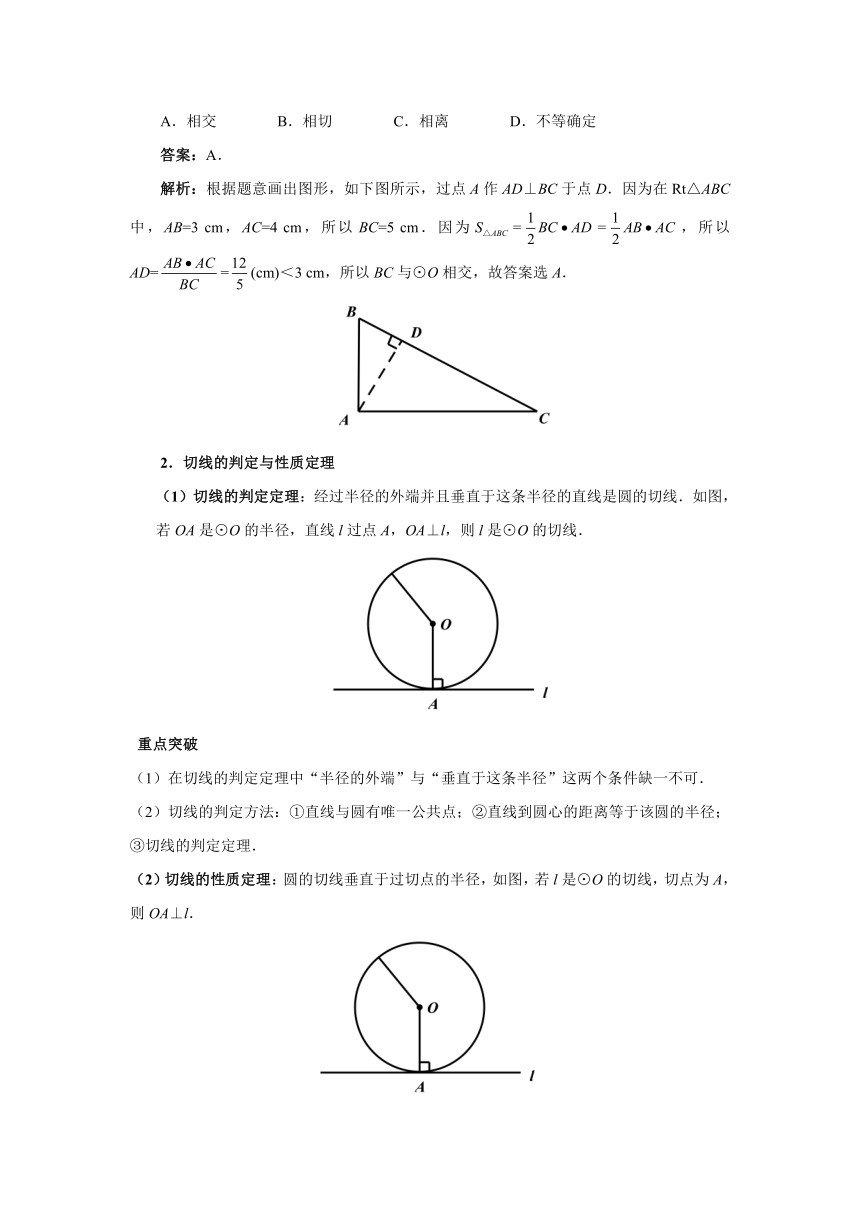
解析:根据题意画出图形,如下图所示,过点A作AD⊥BC于点D.因为在Rt△ABC中,AB=3 cm,AC=4 cm,所以BC=5 cm.因为==,所以AD==(cm)<3 cm,所以BC与⊙O相交,故答案选A.
2.切线的判定与性质定理
(1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.如图,若OA是⊙O的半径,直线l过点A,OA⊥l,则l是⊙O的切线.
重点突破
(1)在切线的判定定理中“半径的外端”与“垂直于这条半径”这两个条件缺一不可.
(2)切线的判定方法:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.
(2)切线的性质定理:圆的切线垂直于过切点的半径,如图,若l是⊙O的切线,切点为A,则OA⊥l.
重点突破
切线的性质:(1)切线与圆只有一个交点;
(2)圆心到切线的距离等于半径;
(3)切线垂直于过切点的半径(切线的性质定理).
例题
1.如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆O交AC于点D.点E为BC的中点,连接DE.求证:DE是半圆O的切线.
答案:证明:连接OD,OE,BD,则OD=OB.因为AB是⊙O的直径,所以∠ADB=90°.所以△BDC是直角三角形,因为点E为BC的中点,所以DE=BC,即DE=BE.因为OD=OB,DE=BE,OE=OE,所以△ODE≌△OBE(SSS).所以∠ODE=∠OBE=90°.所以DE是半圆O的切线.
解析:欲证DE是半圆O的切线,可通过证明点D与圆心O的连线垂直于DE,所以需连接OD.已知点E是BC的中点,可联想到直角三角形中线的性质,结合AB是⊙O的直径,易得△BDC是直角三角形,从而得到DE=BE.又因为OD=OB,从而想到利用全等三角形进行证明,即连接OE,得到△ODE≌△OBE(SSS),从而得出结论.
2.如下图,点O为正方形ABCD的对角线AC上一点,以点O为圆心,OA为半径的⊙O与BC相切于点M.求证:CD与⊙O相切.
答案:证明:过点O作ON⊥CD于点N,连接OM,则OM⊥BC,且OM为半径.因为四边形ABCD是正方形,所以AC是∠BCD的平分线.因为点O在AC上,且ON⊥DC,OM⊥BC,所以ON=OM,即ON是半径,所以CD与⊙O相切.
解析:欲证CD与⊙O相切,可考虑证明点O到CD的距离等于半径,则需构造辅助线:过点O作ON⊥CD于点N,再连接OM,由BC是⊙O的切线,可得OM是⊙O的半径.然后结合正方形的性质即可得出OM=ON,从而得出结论.
3.三角形的内切圆
与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.如图,⊙I就是ΔABC的内切圆.点I叫做ΔABC的内心.
重点突破
(1)三角形的内切圆的圆心是三角形的内角平分线的交点,半径是该交点到三边的距离.三角形的内心到三边的距离都相等.
(2)三角形的内切圆的作法:作三角形的两个内角的平分线,以两个内角的平分线的交点为圆心,以该交点到一边的距离为半径作圆,即可得到三角形的内切圆.
(3)三角形的外心与内心的对比
名称
确定方法
图形
性质
外心
三角形三边的垂直平分线的交点
(1)OA=OB=OC;
(2)外心不一定在三角形的内部
内心
三角形三条角平分线的交点
(1)到三边的距离相等;
(2)内心在三角形的内部
例题
1.已知Rt△ABC的三边长分别为6,8,10,求这个三角形内切圆的半径.
解析:根据题意画出图形.
因为Rt△ABC是⊙O的内切圆,所以OF⊥BC,OD⊥AC,AC⊥BC,且OF=OD=OE.
因为OF⊥BC,OD⊥AC,AC⊥BC,所以四边形CFOD是矩形.
因为OD=OF,所以四边形CFOD是正方形.
设OF=OD=CD=CF=x.
因为AD=AE,BF=BE,所以BF+AD=BE+AE=AB.
则(6-x)+(8-x)=10.解得x=2.
所以这个三角形内切圆的半径为2.
重难点典例剖析
1.直线和圆的位置关系
(1)直线和圆相交、相切、相离的概念
①相交:直线和圆有两个公共点时,直线和圆相交,这条直线叫做圆的割线.
②相切:直线和圆只有一个公共点时,直线和圆相切,这条直线叫做圆的切线,这个公共点叫做切点;
③相离:直线和圆没有公共点时,直线和圆相离.
(2)直线和圆的位置关系
如图,设r是⊙O的半径,d是圆心O到直线l的距离,则:
①直线l和⊙O相交 d
③直线l和⊙O相离 d>r;
重点突破
(1)通过直线和圆的交点的个数来定义直线和圆的三种位置关系是一种定性的描述,比较易懂.
(2)通过比较圆心到直线的距离与半径的大小来说明直线和圆的关系是一种定量的描述,这种描述使得数与形的统一,应用更加广泛.
例题
1.已知⊙O的半径为的3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( ).
A.相交 B.相切 C.相离 D.不等确定
答案:A.
解析:因为2<3,即圆心O到直线l的距离小于⊙O的半径,所以直线l与⊙O相交,故答案选A.
2.在△ABC中,∠A=90°,AB=3 cm,AC=4 cm,若以点A为圆心,3 cm长为半径作⊙A,则BC与⊙A的位置关系是( ).
A.相交 B.相切 C.相离 D.不等确定
答案:A.
解析:根据题意画出图形,如下图所示,过点A作AD⊥BC于点D.因为在Rt△ABC中,AB=3 cm,AC=4 cm,所以BC=5 cm.因为==,所以AD==(cm)<3 cm,所以BC与⊙O相交,故答案选A.
2.切线的判定与性质定理
(1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.如图,若OA是⊙O的半径,直线l过点A,OA⊥l,则l是⊙O的切线.
重点突破
(1)在切线的判定定理中“半径的外端”与“垂直于这条半径”这两个条件缺一不可.
(2)切线的判定方法:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.
(2)切线的性质定理:圆的切线垂直于过切点的半径,如图,若l是⊙O的切线,切点为A,则OA⊥l.
重点突破
切线的性质:(1)切线与圆只有一个交点;
(2)圆心到切线的距离等于半径;
(3)切线垂直于过切点的半径(切线的性质定理).
例题
1.如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆O交AC于点D.点E为BC的中点,连接DE.求证:DE是半圆O的切线.
答案:证明:连接OD,OE,BD,则OD=OB.因为AB是⊙O的直径,所以∠ADB=90°.所以△BDC是直角三角形,因为点E为BC的中点,所以DE=BC,即DE=BE.因为OD=OB,DE=BE,OE=OE,所以△ODE≌△OBE(SSS).所以∠ODE=∠OBE=90°.所以DE是半圆O的切线.
解析:欲证DE是半圆O的切线,可通过证明点D与圆心O的连线垂直于DE,所以需连接OD.已知点E是BC的中点,可联想到直角三角形中线的性质,结合AB是⊙O的直径,易得△BDC是直角三角形,从而得到DE=BE.又因为OD=OB,从而想到利用全等三角形进行证明,即连接OE,得到△ODE≌△OBE(SSS),从而得出结论.
2.如下图,点O为正方形ABCD的对角线AC上一点,以点O为圆心,OA为半径的⊙O与BC相切于点M.求证:CD与⊙O相切.
答案:证明:过点O作ON⊥CD于点N,连接OM,则OM⊥BC,且OM为半径.因为四边形ABCD是正方形,所以AC是∠BCD的平分线.因为点O在AC上,且ON⊥DC,OM⊥BC,所以ON=OM,即ON是半径,所以CD与⊙O相切.
解析:欲证CD与⊙O相切,可考虑证明点O到CD的距离等于半径,则需构造辅助线:过点O作ON⊥CD于点N,再连接OM,由BC是⊙O的切线,可得OM是⊙O的半径.然后结合正方形的性质即可得出OM=ON,从而得出结论.
3.三角形的内切圆
与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.如图,⊙I就是ΔABC的内切圆.点I叫做ΔABC的内心.
重点突破
(1)三角形的内切圆的圆心是三角形的内角平分线的交点,半径是该交点到三边的距离.三角形的内心到三边的距离都相等.
(2)三角形的内切圆的作法:作三角形的两个内角的平分线,以两个内角的平分线的交点为圆心,以该交点到一边的距离为半径作圆,即可得到三角形的内切圆.
(3)三角形的外心与内心的对比
名称
确定方法
图形
性质
外心
三角形三边的垂直平分线的交点
(1)OA=OB=OC;
(2)外心不一定在三角形的内部
内心
三角形三条角平分线的交点
(1)到三边的距离相等;
(2)内心在三角形的内部
例题
1.已知Rt△ABC的三边长分别为6,8,10,求这个三角形内切圆的半径.
解析:根据题意画出图形.
因为Rt△ABC是⊙O的内切圆,所以OF⊥BC,OD⊥AC,AC⊥BC,且OF=OD=OE.
因为OF⊥BC,OD⊥AC,AC⊥BC,所以四边形CFOD是矩形.
因为OD=OF,所以四边形CFOD是正方形.
设OF=OD=CD=CF=x.
因为AD=AE,BF=BE,所以BF+AD=BE+AE=AB.
则(6-x)+(8-x)=10.解得x=2.
所以这个三角形内切圆的半径为2.
