初中数学切线的判定定理微课堂教学设计
图片预览

文档简介
文档名称
初中数学85课题13微课堂教学设计
微课堂课题
切线的判定定理
教学内容预设用时
15分钟
微课堂教学设计
《切线的判定定理》
一、目标设计
1.通过学生自己探究(猜想、类比、演绎)过程,让学生发现切线的判定定理,并能说明方法的正确性。
2.探索并证明切线的判定定理,发展演绎推理能力.
3.体会归纳、转化等数学思想,感悟数学的严谨性,培养勇于探索,大胆创新的精神.
二、过程设计
板块一:引入
(多媒体显示问题)
1.直线与圆有哪三种位置关系?判断的标准是什么?
2.什么叫圆的切线?怎样判定一条直线是不是圆的切线?(学生先观察、猜想,在让学生和教师一道用自制教具进行演示)
通过以上演示探究,我们发现可以用切线的定义来判定一条直线是不是圆的切线,但有时使用起来很不方.为此,我们有必要学习切线的判定定理.
(多媒体显示课题):切线的判定定理
探究新知
上节课学习了“圆心到一条直线的距离等于该圆的半径,则该直线就是圆的一条切线”这一定义。下面请同学们把我们刚刚的实验操作用作图步骤归纳出来:
画出⊙O;在⊙O上任取一点A;连接OA;过点A作直线l⊥OA.(完成后,请同学们猜想,直线l是不是⊙O的切线?它满足哪些条件?).
学生猜想:一条直线满足:经过半径的外端;垂直于这条半径,那么这条直线是圆的切线。(让学生试图用文字语言加以概括)
结合所画图形,引导学生分析:因为直线l⊥OA,所以圆心O到直线l的距离等于OA,而OA正好是圆O的半径,根据“当圆心到直线的距离等于该圆的半径时,直线就是圆的一条切线”可知直线l是圆O的切线.
(多媒体显示)切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.(分析两个条件及几何语言的书写)
提问:生活中你看到哪些现象是直线和圆相切的位置关系的?(学生回答,教师补充)如:下雨天,转动雨伞,雨伞上的水滴会沿着什么方向飞出?车轮和笔直的公路;
磨砂轮上的火花等。
练一练:判断下列说法是否正确.(多媒体显示)
(1)过半径外端的直线是圆的切线.( )
(2)与半径垂直的直线是圆的切线.( )
(3)过半径的端点且与半径垂直的直线是圆的切线.( )
(4)经过直径的端点且与直径垂直的直线是圆的切线( )
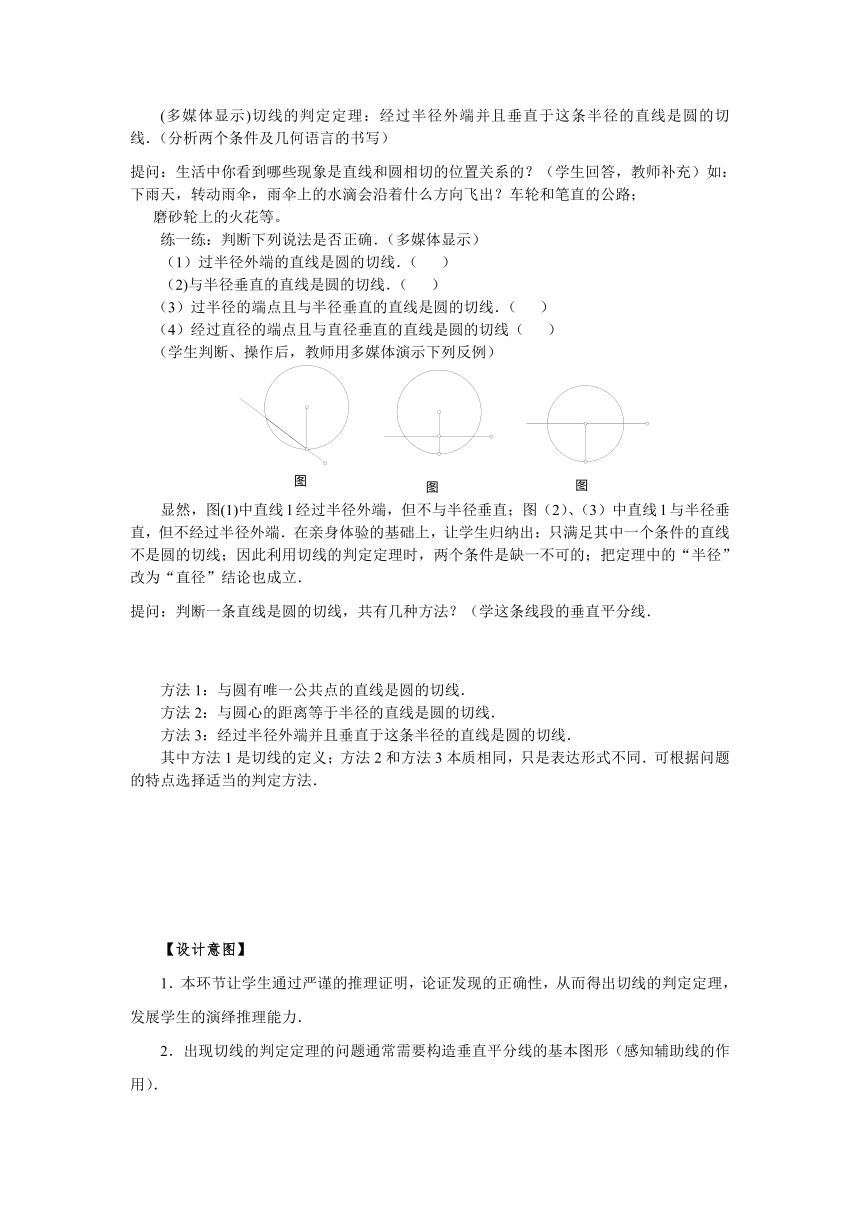
(学生判断、操作后,教师用多媒体演示下列反例)
显然,图(1)中直线l经过半径外端,但不与半径垂直;图(2)、(3)中直线l与半径垂直,但不经过半径外端.在亲身体验的基础上,让学生归纳出:只满足其中一个条件的直线不是圆的切线;因此利用切线的判定定理时,两个条件是缺一不可的;把定理中的“半径”改为“直径”结论也成立.
提问:判断一条直线是圆的切线,共有几种方法?(学这条线段的垂直平分线.
方法1:与圆有唯一公共点的直线是圆的切线.
方法2:与圆心的距离等于半径的直线是圆的切线.
方法3:经过半径外端并且垂直于这条半径的直线是圆的切线.
其中方法1是切线的定义;方法2和方法3本质相同,只是表达形式不同.可根据问题的特点选择适当的判定方法.
【设计意图】
1.本环节让学生通过严谨的推理证明,论证发现的正确性,从而得出切线的判定定理,发展学生的演绎推理能力.
2.出现切线的判定定理的问题通常需要构造垂直平分线的基本图形(感知辅助线的作用).
3.引领学生掌握解决一类问题的规律及方法.
4.体会归纳、转化等数学思想.
【问题预设】学生能比较顺利地完成此环节的证明过程.
【处理策略】此环节教师要着力抛出如下问题引发学生的深思后进行总结提升:
1.要证明线段相等的方法是什么 ?
2.出现证明切线想到什么样的基本图形?
3.此证明过程都渗透了哪些数学思想方法?
4.你能试着总结出此类问题的解题规律及方法吗?这样既能引发学生对前面学过的知识的回顾与运用,又为学生的后续学习奠定了基础;指引了解题方向、明确了解题方法,从而达到举一反三、触类旁通,轻松学习.
三、评价设计
1.通过板块二中的(一)“操作猜想,探索定理”达成教学目标1-----“经历切线的判定定理的探索过程,发展合情推理能力.”
2.通过板块二中的(二)“自主探究,证明定理”达成教学目标2------“探索并证明切线的判定定理,发展演绎推理能力.”
3.通过板块二中的(一)“操作猜想,探索定理”得出命题,让学生体会“归纳”的数学思想方法;通过板块二中的(二)“自主探究,证明定理”,添加辅助线,,让学生体会“转化”的数学思想方法,从而达成教学目标3-----“体会归纳、转化等数学思想,感悟数学的严谨性,培养勇于探索,大胆创新的精神.
微课堂达标检测题
《切线的判定定理》
一、试题计划
【考查的知识点】切线的判定定理.
【考查的能力点】解题分析能力、触类旁通能力、反思提升能力.
【考查的题型】填空题、证明题、开放题.
【考查的试题来源】课本上的练习题及改编整合题
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线
=
三、试题答案
解:(1)证明:如图,连接OA,
∵sin B=,∴∠B=30°,
∵∠AOC=2∠B,∴∠AOC=60°,
∵∠D=30°,
∴∠OAD=180°-∠D-∠AOC=90°,
∴AD是⊙O的切线.
(2)∵OA=OC,∠AOC=60°,
∴△AOC是等边三角形,∴OA=AC=6,
∵∠OAD=90°,∠D=30°,
∴AD=AO=6.
初中数学85课题13微课堂教学设计
微课堂课题
切线的判定定理
教学内容预设用时
15分钟
微课堂教学设计
《切线的判定定理》
一、目标设计
1.通过学生自己探究(猜想、类比、演绎)过程,让学生发现切线的判定定理,并能说明方法的正确性。
2.探索并证明切线的判定定理,发展演绎推理能力.
3.体会归纳、转化等数学思想,感悟数学的严谨性,培养勇于探索,大胆创新的精神.
二、过程设计
板块一:引入
(多媒体显示问题)
1.直线与圆有哪三种位置关系?判断的标准是什么?
2.什么叫圆的切线?怎样判定一条直线是不是圆的切线?(学生先观察、猜想,在让学生和教师一道用自制教具进行演示)
通过以上演示探究,我们发现可以用切线的定义来判定一条直线是不是圆的切线,但有时使用起来很不方.为此,我们有必要学习切线的判定定理.
(多媒体显示课题):切线的判定定理
探究新知
上节课学习了“圆心到一条直线的距离等于该圆的半径,则该直线就是圆的一条切线”这一定义。下面请同学们把我们刚刚的实验操作用作图步骤归纳出来:
画出⊙O;在⊙O上任取一点A;连接OA;过点A作直线l⊥OA.(完成后,请同学们猜想,直线l是不是⊙O的切线?它满足哪些条件?).
学生猜想:一条直线满足:经过半径的外端;垂直于这条半径,那么这条直线是圆的切线。(让学生试图用文字语言加以概括)
结合所画图形,引导学生分析:因为直线l⊥OA,所以圆心O到直线l的距离等于OA,而OA正好是圆O的半径,根据“当圆心到直线的距离等于该圆的半径时,直线就是圆的一条切线”可知直线l是圆O的切线.
(多媒体显示)切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.(分析两个条件及几何语言的书写)
提问:生活中你看到哪些现象是直线和圆相切的位置关系的?(学生回答,教师补充)如:下雨天,转动雨伞,雨伞上的水滴会沿着什么方向飞出?车轮和笔直的公路;
磨砂轮上的火花等。
练一练:判断下列说法是否正确.(多媒体显示)
(1)过半径外端的直线是圆的切线.( )
(2)与半径垂直的直线是圆的切线.( )
(3)过半径的端点且与半径垂直的直线是圆的切线.( )
(4)经过直径的端点且与直径垂直的直线是圆的切线( )
(学生判断、操作后,教师用多媒体演示下列反例)
显然,图(1)中直线l经过半径外端,但不与半径垂直;图(2)、(3)中直线l与半径垂直,但不经过半径外端.在亲身体验的基础上,让学生归纳出:只满足其中一个条件的直线不是圆的切线;因此利用切线的判定定理时,两个条件是缺一不可的;把定理中的“半径”改为“直径”结论也成立.
提问:判断一条直线是圆的切线,共有几种方法?(学这条线段的垂直平分线.
方法1:与圆有唯一公共点的直线是圆的切线.
方法2:与圆心的距离等于半径的直线是圆的切线.
方法3:经过半径外端并且垂直于这条半径的直线是圆的切线.
其中方法1是切线的定义;方法2和方法3本质相同,只是表达形式不同.可根据问题的特点选择适当的判定方法.
【设计意图】
1.本环节让学生通过严谨的推理证明,论证发现的正确性,从而得出切线的判定定理,发展学生的演绎推理能力.
2.出现切线的判定定理的问题通常需要构造垂直平分线的基本图形(感知辅助线的作用).
3.引领学生掌握解决一类问题的规律及方法.
4.体会归纳、转化等数学思想.
【问题预设】学生能比较顺利地完成此环节的证明过程.
【处理策略】此环节教师要着力抛出如下问题引发学生的深思后进行总结提升:
1.要证明线段相等的方法是什么 ?
2.出现证明切线想到什么样的基本图形?
3.此证明过程都渗透了哪些数学思想方法?
4.你能试着总结出此类问题的解题规律及方法吗?这样既能引发学生对前面学过的知识的回顾与运用,又为学生的后续学习奠定了基础;指引了解题方向、明确了解题方法,从而达到举一反三、触类旁通,轻松学习.
三、评价设计
1.通过板块二中的(一)“操作猜想,探索定理”达成教学目标1-----“经历切线的判定定理的探索过程,发展合情推理能力.”
2.通过板块二中的(二)“自主探究,证明定理”达成教学目标2------“探索并证明切线的判定定理,发展演绎推理能力.”
3.通过板块二中的(一)“操作猜想,探索定理”得出命题,让学生体会“归纳”的数学思想方法;通过板块二中的(二)“自主探究,证明定理”,添加辅助线,,让学生体会“转化”的数学思想方法,从而达成教学目标3-----“体会归纳、转化等数学思想,感悟数学的严谨性,培养勇于探索,大胆创新的精神.
微课堂达标检测题
《切线的判定定理》
一、试题计划
【考查的知识点】切线的判定定理.
【考查的能力点】解题分析能力、触类旁通能力、反思提升能力.
【考查的题型】填空题、证明题、开放题.
【考查的试题来源】课本上的练习题及改编整合题
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线
=
三、试题答案
解:(1)证明:如图,连接OA,
∵sin B=,∴∠B=30°,
∵∠AOC=2∠B,∴∠AOC=60°,
∵∠D=30°,
∴∠OAD=180°-∠D-∠AOC=90°,
∴AD是⊙O的切线.
(2)∵OA=OC,∠AOC=60°,
∴△AOC是等边三角形,∴OA=AC=6,
∵∠OAD=90°,∠D=30°,
∴AD=AO=6.
