1.2.1 有理数同步作业
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
1.2.1 有理数同步作业
姓名:__________班级:__________考号:__________
一、选择题
1.-2不是( )
A. 有理数 B. 自然数 C. 整数 D. 负数
2.在0,1,-2,-3.5这四个数中,是负整数的是( )
A. 0 B. 1 C. -2 D. -3.5
3.若a是正数,则-a一定是( )
A. 正数 B. 负数 C. 正数或负数 D. 正数或零或负数
4.既是分数又是正数的是( )
A、+2 B、- C、0 D、2.3
5.下列说法正确的是( )
A. 非负有理数就是正有理数 B. 零表示没有,是有理数
C. 正整数和负整数统称为整数 D. 整数和分数统称为有理数
6.给出下列说法:①0是整数;②-3.5是负分数;③5.4不是正数;④自然数一定是正数;⑤负分数一定是负有理数,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
7.下列语句:(1)所有整数都是正数;(2)分数是有理数;(3)所有的正数都是整数;(4)在有理数中,除了负数就是正数,其中正确的语句个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
8.下列说法正确的是( )
A. 整数就是自然数 B. 0不是自然数
C. 正数和负数统称为有理数 D. 0是整数而不是正数
9.下列说法中,其中不正确的是( )
A. 0是整数 B. 负分数一定是有理数
C. 一个数不是正数,就一定是负数 D. 0是有理数
10.正整数集合与负整数集合合并在一起构成的集合是( )
A.整数集合 B.有理数集合 C.自然数集合 D.以上说法都不对
二、填空题
11.有限小数和无限循环小数统称________________数.
12._________和__________统称为非负数;__________和_________统称为非正数;__________和_________统称为非正整数;_________和__________统称为非负整数.
13.有理数中,最大的负整数是________.
14.把下列各数分别填在相应的横线上:
1,-0.20, ,325,-789,0,-23.13,0.618,-2014,π,0.1010010001….
正数有:______________________________________________________;
分数有:______________________________________________________;
负数有:______________________________________________________;
正整数有:____________________________________________________;
非正数有:_____________________________________________________;
负整数有:_____________________________________________________;
非负数有:_____________________________________________________;
负分数有:_____________________________________________________;
非负整数有:___________________________________________________.
15.观察下面各数列,研究它们各自的变化规律,并接着填出后面的两个数.
(1)1,-1,1,-1,1,-1,1,-1,_________,_________;
(2)2,-4,6,-8,10,-12,14,-16,_________,_________;
(3)1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,_________,_________.
16.(1)有一列数:1,-2,-3,4,-5,-6,7,-8,….那么接下来的3个数分别
是______,_____,______;
(2)有一列数: , , , ,….那么接下来的第7个数是______________.
三、解答题
17.把下列各数分别填入相应的大括号内:
7,3.5, 3.1415,π,0, ,0.03, ,10, ,
自然数集合{ …};
整数集合{ …};
正分数集合{ …};
非正数集合{ …};
有理数集合{ …}.
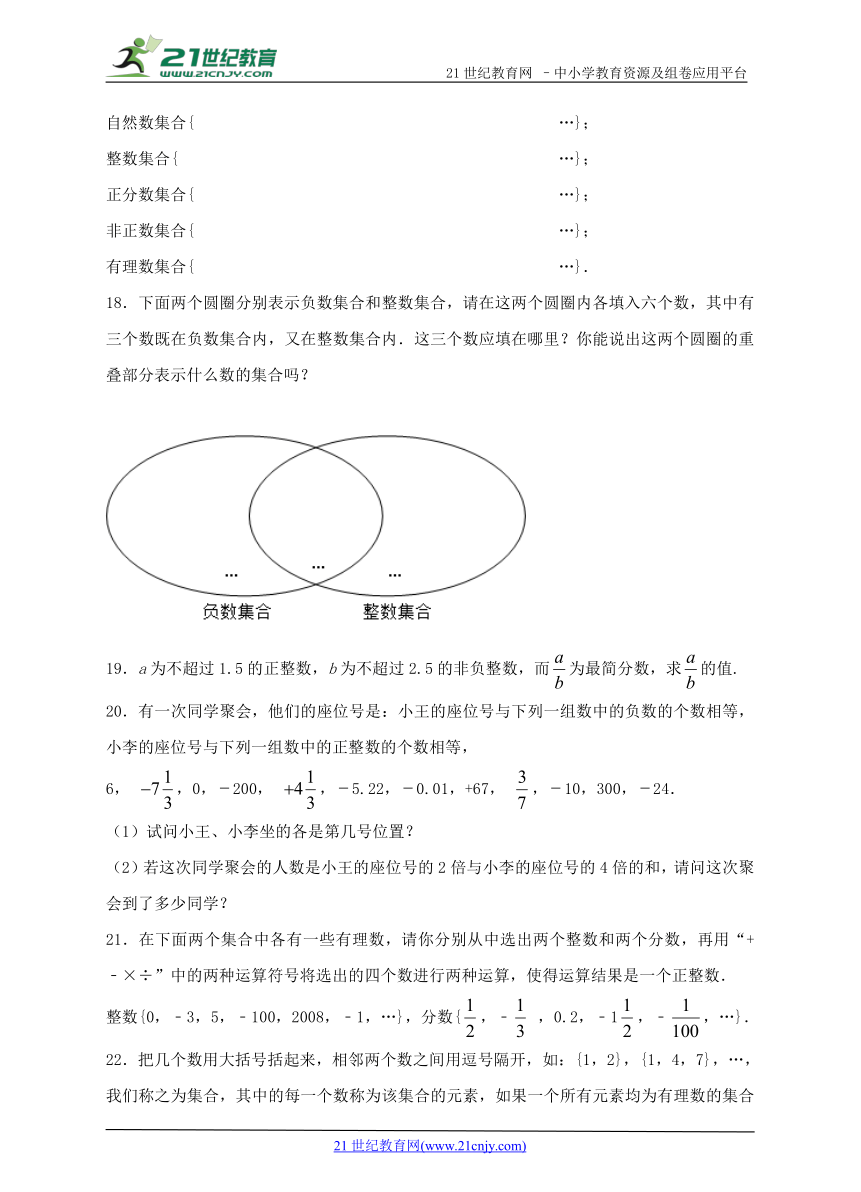
18.下面两个圆圈分别表示负数集合和整数集合,请在这两个圆圈内各填入六个数,其中有三个数既在负数集合内,又在整数集合内.这三个数应填在哪里?你能说出这两个圆圈的重叠部分表示什么数的集合吗?
19.a为不超过1.5的正整数,b为不超过2.5的非负整数,而为最简分数,求的值.
20.有一次同学聚会,他们的座位号是:小王的座位号与下列一组数中的负数的个数相等,小李的座位号与下列一组数中的正整数的个数相等,
6, ,0, 200, , 5.22, 0.01,+67, , 10,300, 24.
(1)试问小王、小李坐的各是第几号位置?
(2)若这次同学聚会的人数是小王的座位号的2倍与小李的座位号的4倍的和,请问这次聚会到了多少同学?
21.在下面两个集合中各有一些有理数,请你分别从中选出两个整数和两个分数,再用“+﹣×÷”中的两种运算符号将选出的四个数进行两种运算,使得运算结果是一个正整数.
整数{0,﹣3,5,﹣100,2008,﹣1,…},分数{,﹣ ,0.2,﹣1,﹣,…}.
22.把几个数用大括号括起来,相邻两个数之间用逗号隔开,如:{1,2},{1,4,7},…,我们称之为集合,其中的每一个数称为该集合的元素,如果一个所有元素均为有理数的集合满足:当有理数x是集合的一个元素时,2016﹣x也必是这个集合的元素,这样的集合我们又称为黄金集合.例如{0,2016}就是一个黄金集合,
(1)集合{2016} 黄金集合,集合{﹣1,2017} 黄金集合;(两空均填“是”或“不是”)
(2)若一个黄金集合中最大的一个元素为4016,则该集合是否存在最小的元素?如果存在,请直接写出答案,否则说明理由;
(3)若一个黄金集合所有元素之和为整数M,且24190<M<24200,则该集合共有几个元素?说明你的理由.
参考答案
1.B
【解析】A选项:因为-2是负整数,所以-2是有理数. 故A选项不符合题意.
B选项:因为自然数包括正整数和0,所以-2不是自然数. 故B选项符合题意.
C选项:因为-2是负整数,所以-2是整数. 故C选项不符合题意.
D选项:因为-2是负整数,所以-2是负数. 故D选项不符合题意.
故本题应选B.
点睛:
本题关键在于准确理解和区别与有理数有关的几个概念. 有理数是整数和分数的统称;自然数事实上就是非负整数. 由此可见,有理数包含自然数,但自然数不包含负整数. 负数事实上是指一切小于零的数,它不仅包含负有理数,还包含除负有理数之外的小于零的数. 因此,负数和有理数之间不是简单的包含与被包含的关系.
2.C
【解析】负整数应该既是负数又是整数. 在本题给出的四个数中,负数是:-2,-3.5;整数是:0,1,-2. 由此可知,在这四个数中,-2是负整数.
故本题应选C.
3.B
【解析】因为负数是在正数前面添加“-”的数,所以当a是正数时,-a是负数.
故本题应选B.
点睛:
本题考查了负数的概念. 负数在形式上是在正数前面添加“-”的数,在意义上是一切小于零的数. 另外,解决涉及字母表示数的题目时,要注意体会字母所代表的实际意义. 字母本身可以表示正数也可以表示负数,切不可看到字母前面有“-”就简单地认为该数是负数.
4.D
【解析】本题考查的是有理数的分类
大于0的数是正数.小数是分数的一种形式,所以既是分数、又是正数的数是,故选D。
5.D
【解析】A选项:非负有理数包括正有理数和零,故A选项错误.
B选项:因为零是整数,所以零是有理数. 这与零的意义并无直接关系. 故B选项错误.
C选项:整数除包括正整数和负整数外还包括零. 故C选项错误.
D选项:在中学阶段,本选项的说法相当于有理数概念的一种表述方式. 故D选项正确.
故本题应选D.
点睛:
本题的一个重点在于正确理解“非负”的意义. 由于正数和负数之间还有零,所以一般情况下在遇到“非负”或“非正”等字眼时一定要注意分析所指代的数中是否包括零. 本题的另一个重点在于理解有理数概念的不同表述. “整数和分数统称为有理数”是有理数概念一种表述方式,其中所谓的“分数”是可以与有限小数或无限循环小数相互转化的.
6.C
【解析】说法①:因为整数包括正整数,负整数和0,所以0是整数. 故说法①正确.
说法②:因为,所以-3.5是负分数. 故说法②正确.
说法③:因为5.4>0,所以5.4是正数. 故说法③错误.
说法④:因为正整数和0是自然数,0不是正数,所以自然数不一定是正数. 故说法④错误.
说法⑤:因为整数和分数统称有理数,所以负分数是负有理数. 故说法⑤正确.
综上所述,正确的说法有①②⑤,共3个.
故本题应选C.
7.A
【解析】语句(1):因为整数包括正整数,负整数和0,所以整数不一定是正数. 故语句(1)错误.
语句(2):因为整数和分数统称有理数,所以分数是有理数. 故语句(2)正确.
语句(3):因为正分数(如: )也是正数,所以正数不一定是整数. 故语句(3)错误.
语句(4):有理数包括正有理数,负有理数和0,0既不是正数也不是负数. 故语句(4)错误.
综上所述,正确的语句只有语句(2).
故本题应选A.
8.D
【解析】A选项:整数不仅包括自然数还包括负整数. 因此,整数不一定是自然数. 故A选项错误.
B选项:因为自然数包括正整数和0,所以0是自然数. 故B选项错误.
C选项:一方面,0是有理数,但0既不是正数也不是负数;另一方面,正数不只包含正有理数,负数也不只包含负有理数. 故C选项错误.
D选项:整数包含正整数,负整数和0. 0既不是正数也不是负数. 故D选项正确.
故本题应选D.
9.C
【解析】A选项:因为整数包含正整数,负整数和0,所以0是整数. 故A选项正确.
B选项:因为整数和分数统称有理数,所以负分数是有理数. 故B选项正确.
C选项:如果一个数不是正数,那么它可以是负数或0. 故C选项错误.
D选项:因为整数和分数统称有理数,0是整数,所以0是有理数. 故D选项正确.
故本题应选C.
10.D
【解析】
试题分析:根据整数的分类即可得到结果.
正整数、负整数和0统称为整数,故选D.
考点:本题考查的是整数的分类
点评:解答本题的关键是注意0的特殊性,0是整数,但既不是正数,也不是负数.
11.有理数
【解析】如果将整数看成小数部分为零的特殊小数,那么有限小数和无限循环小数可以与整数和分数相互转化. 由于整数和分数统称有理数,所以有限小数和无限循环小数统称有理数.
故本题应填写:有理.
12. 0, 正数; 0, 负数; 0, 负整数; 0, 正整数.
【解析】结合所学内容,本题涉及如下结论:
(1) 0和正数统称为非负数;(2) 0和负数统称为非正数;
(3) 0和负整数统称为非正整数;(4) 0和正整数统称为非负整数.
故本题应依次填写:0,正数;0,负数;0,负整数;0,正整数.
13.-1
【解析】有理数中,最大的负整数是___-1____.
14. 1, ,325,0.618,π,0.1010010001…; -0.20, ,-23.13,0.618; -0.20,-789,-23.13,-2014; 1,325; -0.20,-789,0,-23.13,-2014; -789,-2014; 1, ,325,0,0.618,π,0.1010010001…; -0.20,-23.13; 1,325,0.
【解析】按照本题中给出的分类,结合各类型数的定义依次分析各个数的特征,得
(1) 1是正数;1是正整数;1是非负数;1是非负整数.
(2) -0.20是分数;-0.20是负数;-0.20是非正数;-0.20是负分数.
(3) 是正数; 是分数; 是非负数.
(4) 325是正数;325是正整数;325是非负数;325是非负整数.
(5) -789是负数;-789是非正数;-789是负整数.
(6) 0是非正数;0是非负数;0是非负整数.
(7) -23.13是分数;-23.13是负数;-23.13是非正数;-23.13是负分数.
(8) 0.618是正数;0.618是分数;0.618是非负数.
(9) -2014是负数;-2014是非正数;-2014是负整数.
(10) π是正数;π是非负数.
(11) 0.1010010001…是正数;0.1010010001…是非负数.
故本题应进行如下填写:
(正数) 1, ,325,0.618,π,0.1010010001…;
(分数) -0.20, ,-23.13,0.618;
(负数) -0.20,-789,-23.13,-2014;
(正整数) 1,325;
(非正数) -0.20,-789,0,-23.13,-2014;
(负整数) -789,-2014;
(非负数) 1, ,325,0,0.618,π,0.1010010001…;
(负分数) -0.20,-23.13;
(非负整数) 1,325,0.
15. 1, -1; 18, -20; -1, 0.
【解析】(1) 在该数列中,1与-1交替出现,故后面的两个数分别为1,-1.
(2) 该数列可以看作是先将正整数中的偶数从小到大逐个排列起来再从第二个数开始每隔一个数在原数前面添加负号而得到的. 根据这一规律,后面的两个数分别为:18,-20.
(3) 该数列可以看作是以1,0,-1,0为一个基本单元并不断重复而得到的. 根据这一规律,后面的两个数分别为:-1,0.
故本题应依次填写:1,-1;18,-20;-1,0.
点睛:
本题是一道数字规律探索题. 在解决规律探索题的时候,要注意观察题目中已给出的数字的特征以及这些数字和它们所处位置的序数的关系,同时也要注意已知的数字排列的整体特征. 另外,在获得有关规律的初步结论后,要利用已知的数字多次检验相关结论的正确性.
16. 9, -10, 11;
【解析】(1) 这一列数可以看作是先将正整数从小到大逐个排列起来再从第二个数开始每隔一个数在原数前面添加负号而得到的. 根据这一规律,接下来的3个数分别为:9,-10,11.
(2) 对这一列数的分子与分母的规律分别进行讨论.
①这一列数的分子可以看作是将正整数从小到大逐个排列起来而得到的.
②观察这列数的分母可以看出, , , , ,…
因此,这列数的分母可以看作是该分数的分子与其自身之积再加上1而得到的.
根据上述规律,第7个数的分子应为7,第7个数的分母应为,即第7个数应为.
故本题应依次填写:9,-10,11; .
点睛:
本题的难点在于第(2)小题,而第(2)小题的难点在于确定分数分母的变化规律. 在寻找这一规律时要特别注意这些分数的分母与相应的分数在整列数中的位置序数(在本题中相当于相应的分子的数值)的关系. 另外,在探索规律时,一般需要对各个数字进行一定的运算,要特别注意根据已知数的位置序数构造算式的形式,这常常是解决问题的突破口.
17.0,10; 7,0,10, ; 3.5, ,0.03; 7, 3.1415,0, , , ;
7,3.5, 3.1415,0, ,0.03, ,10, ,
【解析】根据题目中给出的各个数的特征和有理数相关的概念,逐个分析题目中给出的数.
(1) -7是整数;-7是非正数;-7是有理数.
(2) 3.5是正分数;3.5是有理数.
(3) -3.1415是非正数;-3.1415是有理数.
(4) π不是有理数,也不是非正数,故π不属于题目中列出的任何集合.
(5) 0是自然数;0是整数;0是非正数;0是有理数.
(6) 是正分数; 是有理数.
(7) 0.03是正分数;0.03是有理数.
(8) 是非正数; 是有理数.
(9) 10是自然数;10是整数;10是有理数.
(10) 是非正数; 是有理数.
(11) 是整数; 是非正数; 是有理数.
试题解析:
自然数集合{0,10,…};
整数集合{-7,0,10, ,…};
正分数集合{3.5, ,0.03,…};
非正数集合{-7,-3.1415,0, , , ,…};
有理数集合{-7,3.5,-3.1415,0, ,0.03, ,10, , ,…}.
点睛:
本题考查了有理数相关的概念. 解决本题的关键是要分清各个集合的概念和范围. 自然数包括0和正整数;整数包括正整数,0和负整数;既是正数也是分数的数称为正分数;非正数包括0和负数;有限小数和无限循环小数统称为有理数. 另外,在解决本题的过程中容易因为粗心而出错,故应做到耐心和细致.
18.答案不唯一
【解析】试题分析:
因为两个圆圈的重叠部分表示既是负数也是整数的数的集合(即负整数集合),所以在图中两个圆圈的重叠部分应填入3个负整数,负数集合的未重叠部分可填入3个负分数,整数集合的未重叠部分应填入3个非负的整数.
试题解析:
(1) 负数集合的未重叠部分可填入:,,;负数集合与整数集合的重叠部分可填入:,,;整数集合的未重叠部分可填入:1,2,3. (注:这部分答案不唯一,填入的数只要符合题意即可,给出的答案供参考)
(2) 这三个既在负数集合内又在整数集合内的数应填在图中两个圆圈的重叠部分中.
(3) 这两个圆圈的重叠部分表示负整数的集合.
点睛:
本题考查了负数和整数两个概念之间的关系. 负数在意义上是指一切小于零的数. 负数包括负整数,负分数以及其他小于零的数. 整数包括正整数,负整数和零. 可见,整数和负数不是简单的包含与被包含的关系,这两个集合的交叉部分是负整数. 在有理数这部分内容中,各种数的集合之间的关系是考查的重点,需要注意理解和掌握
19.
【解析】试题分析:
根据“a为不超过1.5的正整数”容易得到a的值. 根据“b为不超过2.5的非负整数”可以得到b的可能取值. 根据“为最简分数”,将b的可能取值逐个代入,能使为最简分数的b的取值就是b的实际取值. 根据所求得的a和b的值可以得到的值.
试题解析:
因为a为不超过1.5的正整数,又因为在所有正整数中只有1不超过1.5,所以a=1.
点睛:
本题的一个难点在于如何确定字母b的取值. 在解决本题的过程中,利用最简分数的概念对b的可能取值进行了筛选. 最简分数可以简单理解为分子分母不能进行约分的分数. 一般情况下认为分母为1的分数实际上应为整数. 另外,利用题目中给出的条件进行推理从而确定字母的取值也是常见的考查形式,需要熟练掌握.
20.(1)小王的座位号是6,小李的座位号是3; (2)这次聚会到了24人.
【解析】试题分析:
(1) 根据题意并结合相关的概念,逐个分析题目中所给出的各个数的特征,统计其中负数和正整数的个数,从而得到小王和小李的座位号.
(2) 根据第(1)小题得到的小王和小李的座位号,结合题意中聚会人数与这两个座位号的关系,不难写出一个关于聚会人数的算式. 根据该算式进行运算即可得到聚会的人数.
试题解析:
(1) 在题目中所给出的这组数中,负数有: ,-200,-5.22,-0.01,-10,-24,一共有6个. 因此,小王的座位号是6.
在这组数中,正整数有:6,+67,300,一共有3个. 因此,小李的座位号是3.
答:小王的座位号是6,小李的座位号是3.
(2) 因为小王和小李的座位号分别是6和3,所以这次聚会的人数是 (人).
答:这次聚会到了24人.
点睛:
本题解题的关键在于能够在所给出的数中准确地找出所有的负数和正整数. 这个过程不仅需要对负数和正整数概念的准确理解,更需要耐心和细心. 因此,上述过程既是本题的关键也是易错点. 另外,本题中还考查了利用已知的等量关系列式计算的能力,这是今后解应用题的重要基础.
21.3(答案不唯一).
【解析】试题分析:按照题意要求选择数据时,需要选择能凑整的分数,﹣1然后计算.
试题解析:解:选择0,﹣1, ,﹣1 ,
0﹣(﹣1)﹣(﹣1 )+
=1+1+
=3(答案不唯一).
22.(1)不是,是.(2)一个黄金集合中最大的一个元素为4016,则最小的元素为:2016﹣4016=﹣2000.(3)24个
【解析】试题分析:(1)根据有理数a是集合的元素时,2016﹣a也必是这个集合的元素,这样的集合我们称为黄金集合,从而可以可解答本题;
(2)根据2016﹣a,如果a的值越大,则2016﹣a的值越小,从而可以解答本题;
(3)根据题意可知黄金集合都是成对出现的,并且这对对应元素的和为2016,然后通过估算即可解答本题.
解:(1)根据题意可得,2016﹣2016=0,而集合{2016}中没有元素0,故{2016}不是黄金集合;
∵2016﹣2017=﹣1,
∴集合{﹣1,2016}是好的集合.
故答案为:不是,是.
(2)一个黄金集合中最大的一个元素为4016,则该集合存在最小的元素,该集合最小的元素是﹣2000.
∵2016﹣a中a的值越大,则2016﹣a的值越小,
∴一个黄金集合中最大的一个元素为4016,则最小的元素为:2016﹣4016=﹣2000.
(3)该集合共有24个元素.
理由:∵在黄金集合中,如果一个元素为a,则另一个元素为2016﹣a,
∴黄金集合中的元素一定是偶数个.
∵黄金集合中的每一对对应元素的和为:a+2016﹣a=2016,2016×12=24192,2016×13=26208,
又∵一个黄金集合所有元素之和为整数M,且24190<M<24200,
∴这个黄金集合中的元素个数为:12×2=24(个).
考点:有理数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
1.2.1 有理数同步作业
姓名:__________班级:__________考号:__________
一、选择题
1.-2不是( )
A. 有理数 B. 自然数 C. 整数 D. 负数
2.在0,1,-2,-3.5这四个数中,是负整数的是( )
A. 0 B. 1 C. -2 D. -3.5
3.若a是正数,则-a一定是( )
A. 正数 B. 负数 C. 正数或负数 D. 正数或零或负数
4.既是分数又是正数的是( )
A、+2 B、- C、0 D、2.3
5.下列说法正确的是( )
A. 非负有理数就是正有理数 B. 零表示没有,是有理数
C. 正整数和负整数统称为整数 D. 整数和分数统称为有理数
6.给出下列说法:①0是整数;②-3.5是负分数;③5.4不是正数;④自然数一定是正数;⑤负分数一定是负有理数,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
7.下列语句:(1)所有整数都是正数;(2)分数是有理数;(3)所有的正数都是整数;(4)在有理数中,除了负数就是正数,其中正确的语句个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
8.下列说法正确的是( )
A. 整数就是自然数 B. 0不是自然数
C. 正数和负数统称为有理数 D. 0是整数而不是正数
9.下列说法中,其中不正确的是( )
A. 0是整数 B. 负分数一定是有理数
C. 一个数不是正数,就一定是负数 D. 0是有理数
10.正整数集合与负整数集合合并在一起构成的集合是( )
A.整数集合 B.有理数集合 C.自然数集合 D.以上说法都不对
二、填空题
11.有限小数和无限循环小数统称________________数.
12._________和__________统称为非负数;__________和_________统称为非正数;__________和_________统称为非正整数;_________和__________统称为非负整数.
13.有理数中,最大的负整数是________.
14.把下列各数分别填在相应的横线上:
1,-0.20, ,325,-789,0,-23.13,0.618,-2014,π,0.1010010001….
正数有:______________________________________________________;
分数有:______________________________________________________;
负数有:______________________________________________________;
正整数有:____________________________________________________;
非正数有:_____________________________________________________;
负整数有:_____________________________________________________;
非负数有:_____________________________________________________;
负分数有:_____________________________________________________;
非负整数有:___________________________________________________.
15.观察下面各数列,研究它们各自的变化规律,并接着填出后面的两个数.
(1)1,-1,1,-1,1,-1,1,-1,_________,_________;
(2)2,-4,6,-8,10,-12,14,-16,_________,_________;
(3)1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,_________,_________.
16.(1)有一列数:1,-2,-3,4,-5,-6,7,-8,….那么接下来的3个数分别
是______,_____,______;
(2)有一列数: , , , ,….那么接下来的第7个数是______________.
三、解答题
17.把下列各数分别填入相应的大括号内:
7,3.5, 3.1415,π,0, ,0.03, ,10, ,
自然数集合{ …};
整数集合{ …};
正分数集合{ …};
非正数集合{ …};
有理数集合{ …}.
18.下面两个圆圈分别表示负数集合和整数集合,请在这两个圆圈内各填入六个数,其中有三个数既在负数集合内,又在整数集合内.这三个数应填在哪里?你能说出这两个圆圈的重叠部分表示什么数的集合吗?
19.a为不超过1.5的正整数,b为不超过2.5的非负整数,而为最简分数,求的值.
20.有一次同学聚会,他们的座位号是:小王的座位号与下列一组数中的负数的个数相等,小李的座位号与下列一组数中的正整数的个数相等,
6, ,0, 200, , 5.22, 0.01,+67, , 10,300, 24.
(1)试问小王、小李坐的各是第几号位置?
(2)若这次同学聚会的人数是小王的座位号的2倍与小李的座位号的4倍的和,请问这次聚会到了多少同学?
21.在下面两个集合中各有一些有理数,请你分别从中选出两个整数和两个分数,再用“+﹣×÷”中的两种运算符号将选出的四个数进行两种运算,使得运算结果是一个正整数.
整数{0,﹣3,5,﹣100,2008,﹣1,…},分数{,﹣ ,0.2,﹣1,﹣,…}.
22.把几个数用大括号括起来,相邻两个数之间用逗号隔开,如:{1,2},{1,4,7},…,我们称之为集合,其中的每一个数称为该集合的元素,如果一个所有元素均为有理数的集合满足:当有理数x是集合的一个元素时,2016﹣x也必是这个集合的元素,这样的集合我们又称为黄金集合.例如{0,2016}就是一个黄金集合,
(1)集合{2016} 黄金集合,集合{﹣1,2017} 黄金集合;(两空均填“是”或“不是”)
(2)若一个黄金集合中最大的一个元素为4016,则该集合是否存在最小的元素?如果存在,请直接写出答案,否则说明理由;
(3)若一个黄金集合所有元素之和为整数M,且24190<M<24200,则该集合共有几个元素?说明你的理由.
参考答案
1.B
【解析】A选项:因为-2是负整数,所以-2是有理数. 故A选项不符合题意.
B选项:因为自然数包括正整数和0,所以-2不是自然数. 故B选项符合题意.
C选项:因为-2是负整数,所以-2是整数. 故C选项不符合题意.
D选项:因为-2是负整数,所以-2是负数. 故D选项不符合题意.
故本题应选B.
点睛:
本题关键在于准确理解和区别与有理数有关的几个概念. 有理数是整数和分数的统称;自然数事实上就是非负整数. 由此可见,有理数包含自然数,但自然数不包含负整数. 负数事实上是指一切小于零的数,它不仅包含负有理数,还包含除负有理数之外的小于零的数. 因此,负数和有理数之间不是简单的包含与被包含的关系.
2.C
【解析】负整数应该既是负数又是整数. 在本题给出的四个数中,负数是:-2,-3.5;整数是:0,1,-2. 由此可知,在这四个数中,-2是负整数.
故本题应选C.
3.B
【解析】因为负数是在正数前面添加“-”的数,所以当a是正数时,-a是负数.
故本题应选B.
点睛:
本题考查了负数的概念. 负数在形式上是在正数前面添加“-”的数,在意义上是一切小于零的数. 另外,解决涉及字母表示数的题目时,要注意体会字母所代表的实际意义. 字母本身可以表示正数也可以表示负数,切不可看到字母前面有“-”就简单地认为该数是负数.
4.D
【解析】本题考查的是有理数的分类
大于0的数是正数.小数是分数的一种形式,所以既是分数、又是正数的数是,故选D。
5.D
【解析】A选项:非负有理数包括正有理数和零,故A选项错误.
B选项:因为零是整数,所以零是有理数. 这与零的意义并无直接关系. 故B选项错误.
C选项:整数除包括正整数和负整数外还包括零. 故C选项错误.
D选项:在中学阶段,本选项的说法相当于有理数概念的一种表述方式. 故D选项正确.
故本题应选D.
点睛:
本题的一个重点在于正确理解“非负”的意义. 由于正数和负数之间还有零,所以一般情况下在遇到“非负”或“非正”等字眼时一定要注意分析所指代的数中是否包括零. 本题的另一个重点在于理解有理数概念的不同表述. “整数和分数统称为有理数”是有理数概念一种表述方式,其中所谓的“分数”是可以与有限小数或无限循环小数相互转化的.
6.C
【解析】说法①:因为整数包括正整数,负整数和0,所以0是整数. 故说法①正确.
说法②:因为,所以-3.5是负分数. 故说法②正确.
说法③:因为5.4>0,所以5.4是正数. 故说法③错误.
说法④:因为正整数和0是自然数,0不是正数,所以自然数不一定是正数. 故说法④错误.
说法⑤:因为整数和分数统称有理数,所以负分数是负有理数. 故说法⑤正确.
综上所述,正确的说法有①②⑤,共3个.
故本题应选C.
7.A
【解析】语句(1):因为整数包括正整数,负整数和0,所以整数不一定是正数. 故语句(1)错误.
语句(2):因为整数和分数统称有理数,所以分数是有理数. 故语句(2)正确.
语句(3):因为正分数(如: )也是正数,所以正数不一定是整数. 故语句(3)错误.
语句(4):有理数包括正有理数,负有理数和0,0既不是正数也不是负数. 故语句(4)错误.
综上所述,正确的语句只有语句(2).
故本题应选A.
8.D
【解析】A选项:整数不仅包括自然数还包括负整数. 因此,整数不一定是自然数. 故A选项错误.
B选项:因为自然数包括正整数和0,所以0是自然数. 故B选项错误.
C选项:一方面,0是有理数,但0既不是正数也不是负数;另一方面,正数不只包含正有理数,负数也不只包含负有理数. 故C选项错误.
D选项:整数包含正整数,负整数和0. 0既不是正数也不是负数. 故D选项正确.
故本题应选D.
9.C
【解析】A选项:因为整数包含正整数,负整数和0,所以0是整数. 故A选项正确.
B选项:因为整数和分数统称有理数,所以负分数是有理数. 故B选项正确.
C选项:如果一个数不是正数,那么它可以是负数或0. 故C选项错误.
D选项:因为整数和分数统称有理数,0是整数,所以0是有理数. 故D选项正确.
故本题应选C.
10.D
【解析】
试题分析:根据整数的分类即可得到结果.
正整数、负整数和0统称为整数,故选D.
考点:本题考查的是整数的分类
点评:解答本题的关键是注意0的特殊性,0是整数,但既不是正数,也不是负数.
11.有理数
【解析】如果将整数看成小数部分为零的特殊小数,那么有限小数和无限循环小数可以与整数和分数相互转化. 由于整数和分数统称有理数,所以有限小数和无限循环小数统称有理数.
故本题应填写:有理.
12. 0, 正数; 0, 负数; 0, 负整数; 0, 正整数.
【解析】结合所学内容,本题涉及如下结论:
(1) 0和正数统称为非负数;(2) 0和负数统称为非正数;
(3) 0和负整数统称为非正整数;(4) 0和正整数统称为非负整数.
故本题应依次填写:0,正数;0,负数;0,负整数;0,正整数.
13.-1
【解析】有理数中,最大的负整数是___-1____.
14. 1, ,325,0.618,π,0.1010010001…; -0.20, ,-23.13,0.618; -0.20,-789,-23.13,-2014; 1,325; -0.20,-789,0,-23.13,-2014; -789,-2014; 1, ,325,0,0.618,π,0.1010010001…; -0.20,-23.13; 1,325,0.
【解析】按照本题中给出的分类,结合各类型数的定义依次分析各个数的特征,得
(1) 1是正数;1是正整数;1是非负数;1是非负整数.
(2) -0.20是分数;-0.20是负数;-0.20是非正数;-0.20是负分数.
(3) 是正数; 是分数; 是非负数.
(4) 325是正数;325是正整数;325是非负数;325是非负整数.
(5) -789是负数;-789是非正数;-789是负整数.
(6) 0是非正数;0是非负数;0是非负整数.
(7) -23.13是分数;-23.13是负数;-23.13是非正数;-23.13是负分数.
(8) 0.618是正数;0.618是分数;0.618是非负数.
(9) -2014是负数;-2014是非正数;-2014是负整数.
(10) π是正数;π是非负数.
(11) 0.1010010001…是正数;0.1010010001…是非负数.
故本题应进行如下填写:
(正数) 1, ,325,0.618,π,0.1010010001…;
(分数) -0.20, ,-23.13,0.618;
(负数) -0.20,-789,-23.13,-2014;
(正整数) 1,325;
(非正数) -0.20,-789,0,-23.13,-2014;
(负整数) -789,-2014;
(非负数) 1, ,325,0,0.618,π,0.1010010001…;
(负分数) -0.20,-23.13;
(非负整数) 1,325,0.
15. 1, -1; 18, -20; -1, 0.
【解析】(1) 在该数列中,1与-1交替出现,故后面的两个数分别为1,-1.
(2) 该数列可以看作是先将正整数中的偶数从小到大逐个排列起来再从第二个数开始每隔一个数在原数前面添加负号而得到的. 根据这一规律,后面的两个数分别为:18,-20.
(3) 该数列可以看作是以1,0,-1,0为一个基本单元并不断重复而得到的. 根据这一规律,后面的两个数分别为:-1,0.
故本题应依次填写:1,-1;18,-20;-1,0.
点睛:
本题是一道数字规律探索题. 在解决规律探索题的时候,要注意观察题目中已给出的数字的特征以及这些数字和它们所处位置的序数的关系,同时也要注意已知的数字排列的整体特征. 另外,在获得有关规律的初步结论后,要利用已知的数字多次检验相关结论的正确性.
16. 9, -10, 11;
【解析】(1) 这一列数可以看作是先将正整数从小到大逐个排列起来再从第二个数开始每隔一个数在原数前面添加负号而得到的. 根据这一规律,接下来的3个数分别为:9,-10,11.
(2) 对这一列数的分子与分母的规律分别进行讨论.
①这一列数的分子可以看作是将正整数从小到大逐个排列起来而得到的.
②观察这列数的分母可以看出, , , , ,…
因此,这列数的分母可以看作是该分数的分子与其自身之积再加上1而得到的.
根据上述规律,第7个数的分子应为7,第7个数的分母应为,即第7个数应为.
故本题应依次填写:9,-10,11; .
点睛:
本题的难点在于第(2)小题,而第(2)小题的难点在于确定分数分母的变化规律. 在寻找这一规律时要特别注意这些分数的分母与相应的分数在整列数中的位置序数(在本题中相当于相应的分子的数值)的关系. 另外,在探索规律时,一般需要对各个数字进行一定的运算,要特别注意根据已知数的位置序数构造算式的形式,这常常是解决问题的突破口.
17.0,10; 7,0,10, ; 3.5, ,0.03; 7, 3.1415,0, , , ;
7,3.5, 3.1415,0, ,0.03, ,10, ,
【解析】根据题目中给出的各个数的特征和有理数相关的概念,逐个分析题目中给出的数.
(1) -7是整数;-7是非正数;-7是有理数.
(2) 3.5是正分数;3.5是有理数.
(3) -3.1415是非正数;-3.1415是有理数.
(4) π不是有理数,也不是非正数,故π不属于题目中列出的任何集合.
(5) 0是自然数;0是整数;0是非正数;0是有理数.
(6) 是正分数; 是有理数.
(7) 0.03是正分数;0.03是有理数.
(8) 是非正数; 是有理数.
(9) 10是自然数;10是整数;10是有理数.
(10) 是非正数; 是有理数.
(11) 是整数; 是非正数; 是有理数.
试题解析:
自然数集合{0,10,…};
整数集合{-7,0,10, ,…};
正分数集合{3.5, ,0.03,…};
非正数集合{-7,-3.1415,0, , , ,…};
有理数集合{-7,3.5,-3.1415,0, ,0.03, ,10, , ,…}.
点睛:
本题考查了有理数相关的概念. 解决本题的关键是要分清各个集合的概念和范围. 自然数包括0和正整数;整数包括正整数,0和负整数;既是正数也是分数的数称为正分数;非正数包括0和负数;有限小数和无限循环小数统称为有理数. 另外,在解决本题的过程中容易因为粗心而出错,故应做到耐心和细致.
18.答案不唯一
【解析】试题分析:
因为两个圆圈的重叠部分表示既是负数也是整数的数的集合(即负整数集合),所以在图中两个圆圈的重叠部分应填入3个负整数,负数集合的未重叠部分可填入3个负分数,整数集合的未重叠部分应填入3个非负的整数.
试题解析:
(1) 负数集合的未重叠部分可填入:,,;负数集合与整数集合的重叠部分可填入:,,;整数集合的未重叠部分可填入:1,2,3. (注:这部分答案不唯一,填入的数只要符合题意即可,给出的答案供参考)
(2) 这三个既在负数集合内又在整数集合内的数应填在图中两个圆圈的重叠部分中.
(3) 这两个圆圈的重叠部分表示负整数的集合.
点睛:
本题考查了负数和整数两个概念之间的关系. 负数在意义上是指一切小于零的数. 负数包括负整数,负分数以及其他小于零的数. 整数包括正整数,负整数和零. 可见,整数和负数不是简单的包含与被包含的关系,这两个集合的交叉部分是负整数. 在有理数这部分内容中,各种数的集合之间的关系是考查的重点,需要注意理解和掌握
19.
【解析】试题分析:
根据“a为不超过1.5的正整数”容易得到a的值. 根据“b为不超过2.5的非负整数”可以得到b的可能取值. 根据“为最简分数”,将b的可能取值逐个代入,能使为最简分数的b的取值就是b的实际取值. 根据所求得的a和b的值可以得到的值.
试题解析:
因为a为不超过1.5的正整数,又因为在所有正整数中只有1不超过1.5,所以a=1.
点睛:
本题的一个难点在于如何确定字母b的取值. 在解决本题的过程中,利用最简分数的概念对b的可能取值进行了筛选. 最简分数可以简单理解为分子分母不能进行约分的分数. 一般情况下认为分母为1的分数实际上应为整数. 另外,利用题目中给出的条件进行推理从而确定字母的取值也是常见的考查形式,需要熟练掌握.
20.(1)小王的座位号是6,小李的座位号是3; (2)这次聚会到了24人.
【解析】试题分析:
(1) 根据题意并结合相关的概念,逐个分析题目中所给出的各个数的特征,统计其中负数和正整数的个数,从而得到小王和小李的座位号.
(2) 根据第(1)小题得到的小王和小李的座位号,结合题意中聚会人数与这两个座位号的关系,不难写出一个关于聚会人数的算式. 根据该算式进行运算即可得到聚会的人数.
试题解析:
(1) 在题目中所给出的这组数中,负数有: ,-200,-5.22,-0.01,-10,-24,一共有6个. 因此,小王的座位号是6.
在这组数中,正整数有:6,+67,300,一共有3个. 因此,小李的座位号是3.
答:小王的座位号是6,小李的座位号是3.
(2) 因为小王和小李的座位号分别是6和3,所以这次聚会的人数是 (人).
答:这次聚会到了24人.
点睛:
本题解题的关键在于能够在所给出的数中准确地找出所有的负数和正整数. 这个过程不仅需要对负数和正整数概念的准确理解,更需要耐心和细心. 因此,上述过程既是本题的关键也是易错点. 另外,本题中还考查了利用已知的等量关系列式计算的能力,这是今后解应用题的重要基础.
21.3(答案不唯一).
【解析】试题分析:按照题意要求选择数据时,需要选择能凑整的分数,﹣1然后计算.
试题解析:解:选择0,﹣1, ,﹣1 ,
0﹣(﹣1)﹣(﹣1 )+
=1+1+
=3(答案不唯一).
22.(1)不是,是.(2)一个黄金集合中最大的一个元素为4016,则最小的元素为:2016﹣4016=﹣2000.(3)24个
【解析】试题分析:(1)根据有理数a是集合的元素时,2016﹣a也必是这个集合的元素,这样的集合我们称为黄金集合,从而可以可解答本题;
(2)根据2016﹣a,如果a的值越大,则2016﹣a的值越小,从而可以解答本题;
(3)根据题意可知黄金集合都是成对出现的,并且这对对应元素的和为2016,然后通过估算即可解答本题.
解:(1)根据题意可得,2016﹣2016=0,而集合{2016}中没有元素0,故{2016}不是黄金集合;
∵2016﹣2017=﹣1,
∴集合{﹣1,2016}是好的集合.
故答案为:不是,是.
(2)一个黄金集合中最大的一个元素为4016,则该集合存在最小的元素,该集合最小的元素是﹣2000.
∵2016﹣a中a的值越大,则2016﹣a的值越小,
∴一个黄金集合中最大的一个元素为4016,则最小的元素为:2016﹣4016=﹣2000.
(3)该集合共有24个元素.
理由:∵在黄金集合中,如果一个元素为a,则另一个元素为2016﹣a,
∴黄金集合中的元素一定是偶数个.
∵黄金集合中的每一对对应元素的和为:a+2016﹣a=2016,2016×12=24192,2016×13=26208,
又∵一个黄金集合所有元素之和为整数M,且24190<M<24200,
∴这个黄金集合中的元素个数为:12×2=24(个).
考点:有理数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
