人教版初中数学二年级上册12.2三角形全等的判定
文档属性
| 名称 | 人教版初中数学二年级上册12.2三角形全等的判定 |  | |
| 格式 | zip | ||
| 文件大小 | 845.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-11 18:17:10 | ||
图片预览







文档简介
课件50张PPT。 全等三角形的判定全等三角形的性质是?全等三角形的对应边相等,
对应角相等反过来成立吗?本节就来讨论这个问题先任意画出一个△ABC,再画一个
△A’B’C’,使△ABC与△A’B’C’
满足上六个条件中的一个或两个。你
画出的△A’B’C’与△ABC一定全等吗?两个直角三角形,有一个角相等,
它们全等吗?探
究
1有一条边相等的两个三
角形全等吗?一边、一角相等的两个三
角形全等吗?通过画图我们可以发现,满足上述六个
条件中的一个或两个,△ABC与△A’B’C’
不一定全等。满足三个条件呢?能保证
他们全等吗?我们来分情况讨论。
先任意画一个△ABC再画一个△A’B’C’,
使A’B’=AB,B’C’=BC,C’A’=CA。把
画好的△A’B’C’剪下,放到△ABC上,
它们全等吗?
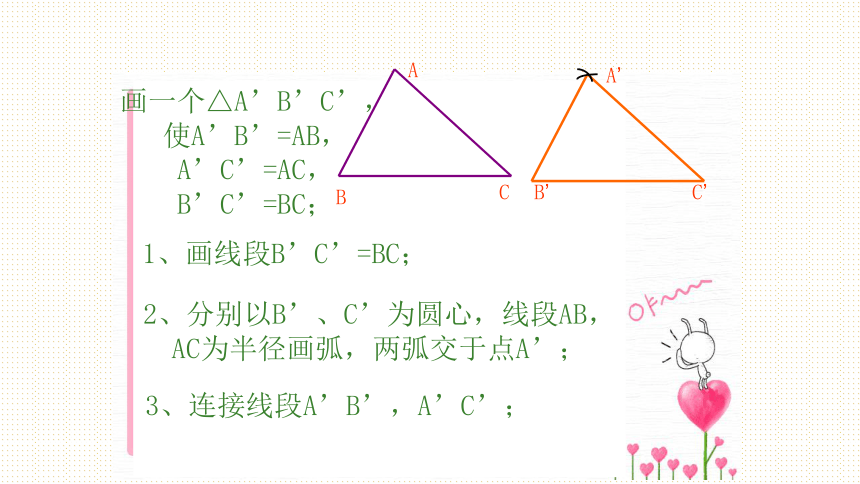
探究2画一个△A’B’C’,
使A’B’=AB,
A’C’=AC,
B’C’=BC;1、画线段B’C’=BC;2、分别以B’、C’为圆心,线段AB,
AC为半径画弧,两弧交于点A’;3、连接线段A’B’,A’C’;CAA’BC’B’ 探究2反应了什么规律?三边对应相等的 两个三角形全等
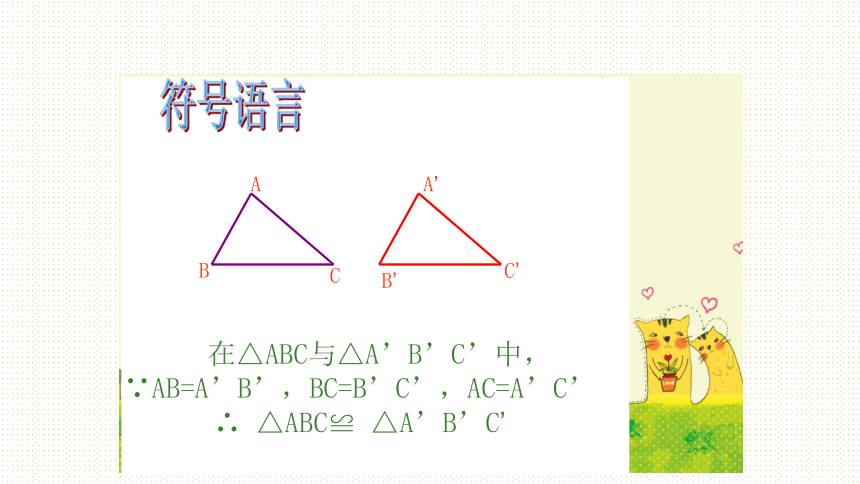
(可简写成SSS)你能写出它的符号语言吗? 在△ABC与△A’B’C’中,
∵AB=A’B’,BC=B’C’,AC=A’C’
∴ △ABC≌ △A’B’C’CAA’BC’B’符号语言我们曾经作过这样的实验,将三根木条钉成
一个三角形木架,这个三角形木架的形状、
大小就不变了。就是说三角形的形状大小
也就确定了,这里用到的就是上面的结论。用上面的结论可以判断两个三角形全等,
判断两个三角形全等的过程,叫做证明
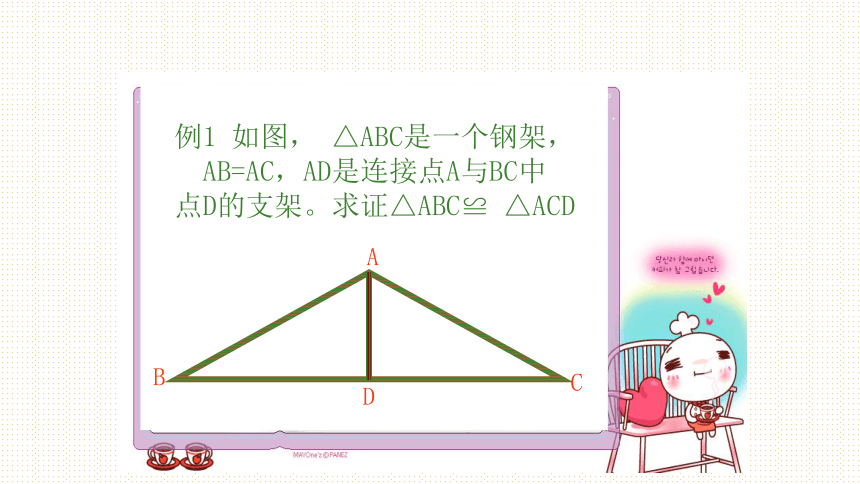
三角形全等。例1 如图, △ABC是一个钢架,
AB=AC,AD是连接点A与BC中
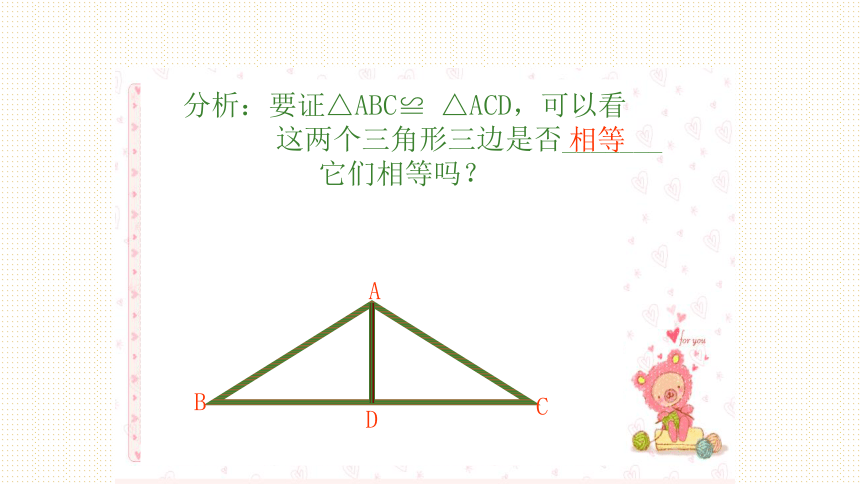
点D的支架。求证△ABC≌ △ACDCABD分析:要证△ABC≌ △ACD,可以看
这两个三角形三边是否_______
它们相等吗?相等证明:∵D是BC的中点,
∴BD=CD﹛AB=AC,在△ABD与△ACD中
BD=CD,AD=AD,∴ △ABD≌ △ACD(SSS)(公共边)(已证)(已知)你学会了吗?从例1可以看出,证明是由题设
(已知)出发,经过一步步推理,
最后推出结论(求证)正确的过程。已知AC=FE,BC=DE,点A、D、B、F在一
条直线上,AD=FB。要用“边边边 ”证明
△ABD≌ △FDE,除了已知中的AC=FE,
BC=DE以还应该有什么条件?怎样才能
得到这个条件?ABCDEF工人师傅常用角尺平分一个任意角。
做法如下:如图,∠AOB是一个任意
角,在边OA、OB上分别取OM=ON,
移动角尺,使角尺两边相同的刻度分
别与M,N重合,过角尺顶点C的射线
OC便是∠AOB的平分线。为什么?练
习先任意画一个△ABC,再画一个
△A’B’C’,使A’B’=AB,∠A’= ∠A,
AC=A’C’,(即使有两边和它们的夹角
对应相等),把画好的△A’B’C’ 剪下,
放到△ABC上,它们全等吗?
探究3CAA’BC’B’画一个△A’B’C’,
使A’B’=AB,
A’C’=AC,
∠A’= ∠A ;1、画∠DA’E= ∠A ;2、在射线A’D上截取A’B’=AB,在
射线A’E上截取A’C’=AC;3、连接线段B’C’; 探究3反应了什么规律?两边和它们的夹角对应相等的 两
个三角形全等(可简写成SAS)你能写出它的符号语言吗?CAA’BC’B’符号语言在△ABC与△A’B’C’中,
∵AB=A’B’,AC=A’C’,∠A’= ∠A
∴ △ABC≌ △A’B’C’例2 如图有一池塘,要测池塘两端
A、B的距离,可先在平地上取一个
可以直接到达A和B的点C,连接AC
并延长到D,使CA=CD;连接BC并延长到E,使CE=CB,连接DE,量
出DE的长就是A、B的距离,为什么?
分析:如果能证明△ABC≌ △DEC,
就可以得到AB____DE =在△ABC与△DEC中,
CA=CD,CB=CE,∠1= ∠2△ABC≌ △DEC还差一个条件是:
_________________证明:﹛CA=CD,在△ABC与△DEF 中
∠1= ∠2 ,CB=CE,∴ △ABC≌ △DEF(SAS)(已知)(对顶角相等)(已知)你学到了什么?从例2可以看出,因为全等三角形
的对应边相等,对应角相等,所以
证明分别属于两个三角形的线段
相等或者角相等的问题,常通过
证明这两个三角形全等来解决。探究4我们知道,两边和它们的夹角对应
相等的两个三角形全等。由“两边及
其中一边的对角对应相等”的条件能
判定两个三角形全等吗?为什么?可以通过画图来回答,还可以通过实验来回答把一长一短的两根细木棍的一端用螺钉铰合
在一起,使长木棍的另一端与射线BC的端
点B重合,适当调整好长木棍与射线BC所成
的角后,固定住长木棍,把短木棍摆起来动动手练
习1、如图,两车从路段AB的一端A出
发,分别向东,向西行进相同的距
离,到达C、D两地,此时C、D到B
的距离相等吗?为什么?ADCB2、如图,点E、F在BC上,BE=CF,
AB=DC,∠B=∠C,求证:∠A=∠DADCBFE探究5先任意画一个△ABC,再画一个
△A’B’C’,使A’B’=AB,∠A’= ∠A,
∠B’= ∠B ,(即两角和它们的夹边
对应相等),把画好的△A’B’C’ 剪下,
放到△ABC上,它们全等吗?
画一个△A’B’C’,
使A’B’=AB,
∠A’= ∠A ,
∠B’= ∠B ;1、画A’B’=AB ;2、在A’B’同旁画∠DA’B’=∠A ,
∠EB’A’= ∠B ,A’D,B’E交于点C’;ABCA’B’C’E’D’两角和它们的夹边对应相等的 两
个三角形全等(可简写成ASA)你能写出它的符号语言吗?CAA’BC’B’ 在△ABC与△A’B’C’中,
∵ ∠A’= ∠A ,AB=A’B’, ∠B’= ∠B ,
∴ △ABC≌ △A’B’C’探究6 在△ABC与△DEF中,∠A= ∠D,∠B= ∠E ,
BC=EF, △ABC与△DEF全等吗?能利用角
边角的条件证明你的结论吗?CADBFE两个角和其中一个角的对边对应
相等的 两个三角形全等
(可简写成AAS)CAA’BC’B’ 在△ABC与△A’B’C’中,
∵ ∠A’= ∠A ,∠B’= ∠B , BC=B’C’,
∴ △ABC≌ △A’B’C’例3 如图,D在AB上,E在AC上,
AB=AC,∠B= ∠C,求证AD=AE
ABCDEABCDE分析:如果能证明△ABE_____△ACD,
就可以得到AB____DE ≌= ﹛AB=AC,在△ABE与△ACD 中
∠B= ∠C ,∠A= ∠A,∴ △ABE≌ △ACD(ASA)(已知)( )(已知)证明:公共角∴AD=AE( 全等三角形对应边相等) 探究7三角对应相等 的两个三角形全等吗?
现在我们学了哪些判定全等的方法?判定两个三角形全等的方法1、SSS:三边对应相等2、SAS 两边及夹角对应相等3、ASA两角夹边对应相等4、AAS 两角及一角的对边对应相等1、如图,要测量河两岸相对两点A,B两
点的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A,C,E在一条直线上,这时
测得DE的长就是AB的长,为什么?ABCDEF2、 如图,AB⊥BC, AD⊥DC ,
∠1= ∠2,求证AB=AD
12ABCD分析:如果能证明
△ABC_____△ACD,
就可以得到AB____AD ≌= 对于两个直角三角形,除了直角相等的
条件外,还要满足几个条件,这两个直角
三角形就全等了?讨论ABCDEF由三角形全等的条件判断,对于两个直角
三角形,满足一边一锐角对应相等,或两
直角边对应相等,这两个直角三角形
全等吗?如果满足斜边和一条直角边
对应相等,这两个直角三角形全等吗?探究8先任意画一个RT△ABC,使∠C=90°,再画一个RT△A’B’C’,使A’B’=AB,BC= B‘C’,把画好的△A’B’C’ 剪下,放到△ABC上,它们全等吗?
画一个RT△A’B’C’,
使B‘C’=BC,
A‘B’= AB;1、画∠MC’N= 90°;2、在射线C‘M上取B’C‘=BC 3、以B‘为圆心,AB为半径画弧,交射线C’N于点A‘ 4、连接A‘B’ ABCA’B’C’NM斜边和一条直角边对应相等
的两个直角三角形全等
(可简写成斜边、直角边或HL)你能写出它的符号语言吗? 在RT△ABC与RT△A’B’C’中,
∠C=∠C=90°
∵ AB=A’B’, BC= B’C‘,
∴RT△ABC≌RT△A’B’C’符号语言例4 如图,AC⊥BC, BD⊥AD ,
AC= BD,求证BC=AD
ABCD﹛AC=BD,在RT△ABC与RT△BAD 中
AB= BA ,∴ RT△ABC ≌ RT△BAD (HL)(已知)(公共边)证明:∵ AC⊥BC,BD⊥AD
∴ ∠C=∠D=90° ∴BC=AD ( 全等三角形对应边相等)1、如图,C是路段AB的中点,两人
从C同时出发,以相同的速度分别沿两
条直线行走,并同时到达D,E两地,
DA⊥AB,EB⊥AB,D,E与路
段AB的距离相等吗?为什么?DBCAE2 如图,AB=CD, AE⊥BC,
DF⊥BC,CE= BF,求证AE=DF
DBCAEF 这节课你学到了什么?1、怎样判定三角形全等?2、怎样判定直角三角形全等?3、证明线段、角相等常用什么方法
对应角相等反过来成立吗?本节就来讨论这个问题先任意画出一个△ABC,再画一个
△A’B’C’,使△ABC与△A’B’C’
满足上六个条件中的一个或两个。你
画出的△A’B’C’与△ABC一定全等吗?两个直角三角形,有一个角相等,
它们全等吗?探
究
1有一条边相等的两个三
角形全等吗?一边、一角相等的两个三
角形全等吗?通过画图我们可以发现,满足上述六个
条件中的一个或两个,△ABC与△A’B’C’
不一定全等。满足三个条件呢?能保证
他们全等吗?我们来分情况讨论。
先任意画一个△ABC再画一个△A’B’C’,
使A’B’=AB,B’C’=BC,C’A’=CA。把
画好的△A’B’C’剪下,放到△ABC上,
它们全等吗?
探究2画一个△A’B’C’,
使A’B’=AB,
A’C’=AC,
B’C’=BC;1、画线段B’C’=BC;2、分别以B’、C’为圆心,线段AB,
AC为半径画弧,两弧交于点A’;3、连接线段A’B’,A’C’;CAA’BC’B’ 探究2反应了什么规律?三边对应相等的 两个三角形全等
(可简写成SSS)你能写出它的符号语言吗? 在△ABC与△A’B’C’中,
∵AB=A’B’,BC=B’C’,AC=A’C’
∴ △ABC≌ △A’B’C’CAA’BC’B’符号语言我们曾经作过这样的实验,将三根木条钉成
一个三角形木架,这个三角形木架的形状、
大小就不变了。就是说三角形的形状大小
也就确定了,这里用到的就是上面的结论。用上面的结论可以判断两个三角形全等,
判断两个三角形全等的过程,叫做证明
三角形全等。例1 如图, △ABC是一个钢架,
AB=AC,AD是连接点A与BC中
点D的支架。求证△ABC≌ △ACDCABD分析:要证△ABC≌ △ACD,可以看
这两个三角形三边是否_______
它们相等吗?相等证明:∵D是BC的中点,
∴BD=CD﹛AB=AC,在△ABD与△ACD中
BD=CD,AD=AD,∴ △ABD≌ △ACD(SSS)(公共边)(已证)(已知)你学会了吗?从例1可以看出,证明是由题设
(已知)出发,经过一步步推理,
最后推出结论(求证)正确的过程。已知AC=FE,BC=DE,点A、D、B、F在一
条直线上,AD=FB。要用“边边边 ”证明
△ABD≌ △FDE,除了已知中的AC=FE,
BC=DE以还应该有什么条件?怎样才能
得到这个条件?ABCDEF工人师傅常用角尺平分一个任意角。
做法如下:如图,∠AOB是一个任意
角,在边OA、OB上分别取OM=ON,
移动角尺,使角尺两边相同的刻度分
别与M,N重合,过角尺顶点C的射线
OC便是∠AOB的平分线。为什么?练
习先任意画一个△ABC,再画一个
△A’B’C’,使A’B’=AB,∠A’= ∠A,
AC=A’C’,(即使有两边和它们的夹角
对应相等),把画好的△A’B’C’ 剪下,
放到△ABC上,它们全等吗?
探究3CAA’BC’B’画一个△A’B’C’,
使A’B’=AB,
A’C’=AC,
∠A’= ∠A ;1、画∠DA’E= ∠A ;2、在射线A’D上截取A’B’=AB,在
射线A’E上截取A’C’=AC;3、连接线段B’C’; 探究3反应了什么规律?两边和它们的夹角对应相等的 两
个三角形全等(可简写成SAS)你能写出它的符号语言吗?CAA’BC’B’符号语言在△ABC与△A’B’C’中,
∵AB=A’B’,AC=A’C’,∠A’= ∠A
∴ △ABC≌ △A’B’C’例2 如图有一池塘,要测池塘两端
A、B的距离,可先在平地上取一个
可以直接到达A和B的点C,连接AC
并延长到D,使CA=CD;连接BC并延长到E,使CE=CB,连接DE,量
出DE的长就是A、B的距离,为什么?
分析:如果能证明△ABC≌ △DEC,
就可以得到AB____DE =在△ABC与△DEC中,
CA=CD,CB=CE,∠1= ∠2△ABC≌ △DEC还差一个条件是:
_________________证明:﹛CA=CD,在△ABC与△DEF 中
∠1= ∠2 ,CB=CE,∴ △ABC≌ △DEF(SAS)(已知)(对顶角相等)(已知)你学到了什么?从例2可以看出,因为全等三角形
的对应边相等,对应角相等,所以
证明分别属于两个三角形的线段
相等或者角相等的问题,常通过
证明这两个三角形全等来解决。探究4我们知道,两边和它们的夹角对应
相等的两个三角形全等。由“两边及
其中一边的对角对应相等”的条件能
判定两个三角形全等吗?为什么?可以通过画图来回答,还可以通过实验来回答把一长一短的两根细木棍的一端用螺钉铰合
在一起,使长木棍的另一端与射线BC的端
点B重合,适当调整好长木棍与射线BC所成
的角后,固定住长木棍,把短木棍摆起来动动手练
习1、如图,两车从路段AB的一端A出
发,分别向东,向西行进相同的距
离,到达C、D两地,此时C、D到B
的距离相等吗?为什么?ADCB2、如图,点E、F在BC上,BE=CF,
AB=DC,∠B=∠C,求证:∠A=∠DADCBFE探究5先任意画一个△ABC,再画一个
△A’B’C’,使A’B’=AB,∠A’= ∠A,
∠B’= ∠B ,(即两角和它们的夹边
对应相等),把画好的△A’B’C’ 剪下,
放到△ABC上,它们全等吗?
画一个△A’B’C’,
使A’B’=AB,
∠A’= ∠A ,
∠B’= ∠B ;1、画A’B’=AB ;2、在A’B’同旁画∠DA’B’=∠A ,
∠EB’A’= ∠B ,A’D,B’E交于点C’;ABCA’B’C’E’D’两角和它们的夹边对应相等的 两
个三角形全等(可简写成ASA)你能写出它的符号语言吗?CAA’BC’B’ 在△ABC与△A’B’C’中,
∵ ∠A’= ∠A ,AB=A’B’, ∠B’= ∠B ,
∴ △ABC≌ △A’B’C’探究6 在△ABC与△DEF中,∠A= ∠D,∠B= ∠E ,
BC=EF, △ABC与△DEF全等吗?能利用角
边角的条件证明你的结论吗?CADBFE两个角和其中一个角的对边对应
相等的 两个三角形全等
(可简写成AAS)CAA’BC’B’ 在△ABC与△A’B’C’中,
∵ ∠A’= ∠A ,∠B’= ∠B , BC=B’C’,
∴ △ABC≌ △A’B’C’例3 如图,D在AB上,E在AC上,
AB=AC,∠B= ∠C,求证AD=AE
ABCDEABCDE分析:如果能证明△ABE_____△ACD,
就可以得到AB____DE ≌= ﹛AB=AC,在△ABE与△ACD 中
∠B= ∠C ,∠A= ∠A,∴ △ABE≌ △ACD(ASA)(已知)( )(已知)证明:公共角∴AD=AE( 全等三角形对应边相等) 探究7三角对应相等 的两个三角形全等吗?
现在我们学了哪些判定全等的方法?判定两个三角形全等的方法1、SSS:三边对应相等2、SAS 两边及夹角对应相等3、ASA两角夹边对应相等4、AAS 两角及一角的对边对应相等1、如图,要测量河两岸相对两点A,B两
点的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A,C,E在一条直线上,这时
测得DE的长就是AB的长,为什么?ABCDEF2、 如图,AB⊥BC, AD⊥DC ,
∠1= ∠2,求证AB=AD
12ABCD分析:如果能证明
△ABC_____△ACD,
就可以得到AB____AD ≌= 对于两个直角三角形,除了直角相等的
条件外,还要满足几个条件,这两个直角
三角形就全等了?讨论ABCDEF由三角形全等的条件判断,对于两个直角
三角形,满足一边一锐角对应相等,或两
直角边对应相等,这两个直角三角形
全等吗?如果满足斜边和一条直角边
对应相等,这两个直角三角形全等吗?探究8先任意画一个RT△ABC,使∠C=90°,再画一个RT△A’B’C’,使A’B’=AB,BC= B‘C’,把画好的△A’B’C’ 剪下,放到△ABC上,它们全等吗?
画一个RT△A’B’C’,
使B‘C’=BC,
A‘B’= AB;1、画∠MC’N= 90°;2、在射线C‘M上取B’C‘=BC 3、以B‘为圆心,AB为半径画弧,交射线C’N于点A‘ 4、连接A‘B’ ABCA’B’C’NM斜边和一条直角边对应相等
的两个直角三角形全等
(可简写成斜边、直角边或HL)你能写出它的符号语言吗? 在RT△ABC与RT△A’B’C’中,
∠C=∠C=90°
∵ AB=A’B’, BC= B’C‘,
∴RT△ABC≌RT△A’B’C’符号语言例4 如图,AC⊥BC, BD⊥AD ,
AC= BD,求证BC=AD
ABCD﹛AC=BD,在RT△ABC与RT△BAD 中
AB= BA ,∴ RT△ABC ≌ RT△BAD (HL)(已知)(公共边)证明:∵ AC⊥BC,BD⊥AD
∴ ∠C=∠D=90° ∴BC=AD ( 全等三角形对应边相等)1、如图,C是路段AB的中点,两人
从C同时出发,以相同的速度分别沿两
条直线行走,并同时到达D,E两地,
DA⊥AB,EB⊥AB,D,E与路
段AB的距离相等吗?为什么?DBCAE2 如图,AB=CD, AE⊥BC,
DF⊥BC,CE= BF,求证AE=DF
DBCAEF 这节课你学到了什么?1、怎样判定三角形全等?2、怎样判定直角三角形全等?3、证明线段、角相等常用什么方法
