11.1.1三角形的边 同步作业
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
11.1.1三角形的边同步作业
姓名:__________班级:__________考号:__________
一、选择题
1.下面是小明用三根火柴组成的图形,其中符合三角形概念的是( )
A. (A) B. (B) C. (C) D. (D)
2.2.已知三角形两边长分别为3和8,则该三角形第三边的长可能是( )
A. 5 B. 10 C. 11 D. 12
3.三角形是( )
A. 连接任意三角形组成的图形
B. 由不在同一条直线上的三条线段首尾顺次相接所组成的的图形
C. 由三条线段组成的图形
D. 以上说法均不对
4.若△ABC三条边的长度分别为m,n,p,且,则这个三角形为( )
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 等腰直角三角形
5.试用学过的知识判断,下列说法正确的是( )
A. 一个直角三角形一定不是等腰三角形 B. 一个等腰三角形一定不是锐角三角形
C. 一个等腰三角形一定不是等腰三角形 D. 一个等腰三角形一定不是钝角三角形
6.一个三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是( )
A. 2 B. 3 C. 4 D. 8
7.下列长度的三条线段能组成三角形的是( )
A. 1,2,3 B. 2,2,4 C. 3,4,5 D. 3,4,8
8.下列各组数据能作为一个等腰三角形各边长的是( )
A. 1,1,2 B. 4,2,4 C. 2,3,4 D. 3,3,7
9.如图,三角形被木板遮住一部分,这个三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 以上都有可能
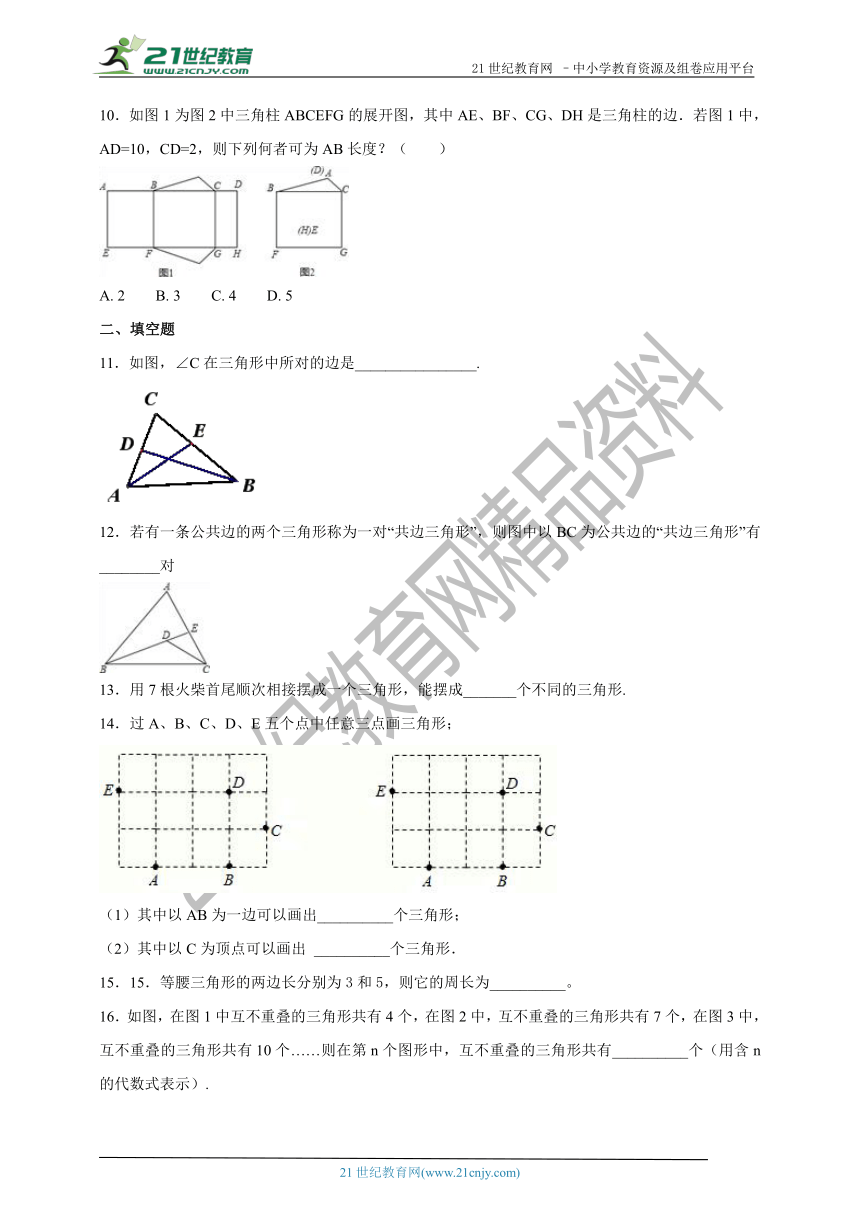
10.如图1为图2中三角柱ABCEFG的展开图,其中AE、BF、CG、DH是三角柱的边.若图1中,AD=10,CD=2,则下列何者可为AB长度?( )
A. 2 B. 3 C. 4 D. 5
二、填空题
11.如图,∠C在三角形中所对的边是________________.
12.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有________对
13.用7根火柴首尾顺次相接摆成一个三角形,能摆成_______个不同的三角形.
14.过A、B、C、D、E五个点中任意三点画三角形;
(1)其中以AB为一边可以画出__________个三角形;
(2)其中以C为顶点可以画出 __________个三角形.
15.15.等腰三角形的两边长分别为3和5,则它的周长为__________。
16.如图,在图1中互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个……则在第n个图形中,互不重叠的三角形共有__________个(用含n的代数式表示).
17.如图,图1中共有3个三角形,图2中共有6个三角形,图3中共有10个三角形,…,以此类推,则图6中共有 __________ 个三角形.
18.平面上有5个点,其中任意三点都不在同一条直线上,则这些点共可组成__________个不同的三角形.
三、解答题
19.一个三角形三边长之比为2:3:4,周长为36cm,求此三角形的三边长.
20.a,b,c分别为△ABC的三边,且满足a+b=3c﹣2,a﹣b=2c﹣6.
(1)求c的取值范围;
(2)若△ABC的周长为18,求c的值.
参考答案
1.C
【解析】∵由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形,
∴C符合三角形的概念.
故选C.
2.B
【解析】试题分析:根据三角形的第三边大于两边之差,而小于两边之和求得第三边的取值范围,再进一步选择.
解:根据三角形的三边关系,得
第三边大于:8﹣3=5,而小于:3+8=11.
则此三角形的第三边可能是:10.
故选:B.
点评:本题考查了三角形的三边关系,即三角形的第三边大于两边之差,而小于两边之和,此题基础题,比较简单.
3.B
【解析】试题解析:因为三角形的定义是:由不在同一条直线上的三条线段首尾顺次相接所成的图形.
故选B.
4.B
【解析】∵|m n|+(n p)2=0,
∴m n=0,n p=0,
∴m=n,n=p,
∴m=n=p,
∴△ABC为等边三角形。
故选B.
点睛:本题可根据非负数的性质“两个非负数相加,和为0,这两个非负数的值都为0.”得出m、n、p的关系,再判断三角形的类型.
5.D
【解析】A、如等腰直角三角形,既是直角三角形,也是等腰三角形,故该选项错误;
B、如等边三角形,既是等腰三角形,也是锐角三角形,故该选项错误;
C、如顶角是120°的等腰三角形,是钝角三角形,也是等腰三角形,故该选项错误;
D、一个等边三角形的三个角都是60°,故该选项正确.
故选D.
6.C
【解析】试题分析:由三角形的三边关系可得5-3<第三边长<3+5,即2<第三边长<8,又因第三边长是偶数,所以第三边长可为4,6,故答案选C.
考点:三角形的三边关系.
7.C
【解析】试题分析:根据三角形的三边满足两边之和大于第三边来进行判断.
解:A、1+2=3,不能构成三角形,故A错误;
B、2+2=4,不能构成三角形,故B错误;
C、3+4>5,能构成三角形,故C正确;
D、3+4<8,不能构成三角形,故D错误.
故选C.
考点:三角形三边关系.
8.B
【解析】A选项:因为1+1=2,所以本组数据不可以构成等腰三角形;故本选项错误;
B选项:因为4﹣4<2<4+4,所以本组数据可以构成等腰三角形;故本选项正确;
C选项:因为这个三角形没有一组相等的边,所以构不成等腰三角形;故本选项错误;
D选项:因为3+3<7,所以本组数据不可以构成等腰三角形;故本选项错误;
故选B.
9.D
【解析】从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角,
故选D.
10.C
【解析】由图可知,AD=AB+BC+CD,
∵AD=10,CD=2,
∴AB+BC=8,
设AB=x,则BC=8 x,
所以 ,
解不等式①得x>3,
解不等式②得,x<5,
所以,不等式组的解集是3综合各选项,只有C符合。
故选C.
点睛:根据图形先求出AB与BC的和,然后设AB=x,表示出BC=8-x,然后利用三角形的任意两边之和大于第三边,两边之差小于第三边列出不等式组,求解得到AB的取值范围,即可得解.
11.AE,BD,AB
【解析】在△ABC中, ∠C的对边是AB; 在△ACE中, ∠C的对边是AE在△BCD中, ∠C的对边是BD;
故答案为: AE,BD,AB
12.3
【解析】图中以BC为公共边的”共边三角形”有△ABC,△DBC,△EBC,共3对.故选B.
13.2
【解析】用7根火柴首尾顺次相接摆成一个三角形,可以摆出两个不同的等腰三角形,
即边长分别为:3,3,1;2,2,3两种三角形.
故本题答案为:2.
14.(1)3(2)6
【解析】试题分析:
(1)根据三角形定义,再选择一个点,然后顺次连接即可画出图形;
(2)根据三角形的定义,再A、B、D、E中任意选择两个点,然后顺次连接即可画出图形.
(1)如图,以AB为一边的三角形有△ABC、△ABD、△ABE共3个;
(2)如图,以点C为顶点的三角形有△ABC、△BEC、△BCD、△ACE、△ACD、△CDE共6个.
故答案为:(1)3,(2)6.
15.11或13
【解析】试题分析:题目给出等腰三角形有两条边长为3和5,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解:有两种情况:①腰长为3,底边长为5,三边为:3,3,5可构成三角形,周长=3+3+5=11;
②腰长为5,底边长为3,三边为:5,5,3可构成三角形,周长=5+5+3=13.
故答案为:11或13.
考点:三角形三边关系;等腰三角形的性质.
16.(3n+1)
【解析】试题分析:观察图形可得,第1个图形中,互不重叠的三角形共有4个,第2个图形中,互不重叠的三角形共有4+3=7个,第3个图形中,互不重叠的三角形共有4+3×2=10个,…根据这个规律可得在第n个图形中,互不重叠的三角形共有4+3(n﹣1)=3n+1.
考点:规律探究题.
17.28
【解析】解:由已知通过观察得:
图1有: 个三角形,
图2有: 个三角形,
图3有: 个三角形,
所以图6中共有: 个三角形,
故答案为:28.
18.10
【解析】解:∵平面上有5个点,其中任意三点都不在同一条直线上,
∴这些点共可组成5×(5-1)÷2=10个不同的三角形.
点睛:数三角形的个数,可以按照数线段条数的方法,如果平面上有5个点,其中任意三点都不在同一条直线上,那么就有 条线段,得到个三角形.
19.8cm,12cm,16cm.
【解析】试题分析:设三边长分别为2x,3x,4x,根据周长为36cm,可得出方程,解出即可.
设三边长分别为2x,3x,4x,
由题意得,2x+3x+4x=36,
解得:x=4.
故三边长为:8cm,12cm,16cm.
点睛:本题考查了一元一次方程的几何应用及见比设参的数学思想, 因为角形三边长之比为2:3:4,所以可设三边长分别为2x,3x,4x,根据周长为36cm,可得出方程求解即可.
20.(1)1<c<6(2)c=5
【解析】【试题分析】(1)利用三角形两边之和大于第三边,两边之差小于第三边,得不等式组解得1
【试题解析】
(1)由题意得解得1
(2)由题意得3c-2+c=18,解得c=5.
【方法点睛】本题目涉及三角形的边的综合题,将三角形的三边关系与不等式组、方程三者巧妙的结合起来.实属难得,但难度不大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
11.1.1三角形的边同步作业
姓名:__________班级:__________考号:__________
一、选择题
1.下面是小明用三根火柴组成的图形,其中符合三角形概念的是( )
A. (A) B. (B) C. (C) D. (D)
2.2.已知三角形两边长分别为3和8,则该三角形第三边的长可能是( )
A. 5 B. 10 C. 11 D. 12
3.三角形是( )
A. 连接任意三角形组成的图形
B. 由不在同一条直线上的三条线段首尾顺次相接所组成的的图形
C. 由三条线段组成的图形
D. 以上说法均不对
4.若△ABC三条边的长度分别为m,n,p,且,则这个三角形为( )
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 等腰直角三角形
5.试用学过的知识判断,下列说法正确的是( )
A. 一个直角三角形一定不是等腰三角形 B. 一个等腰三角形一定不是锐角三角形
C. 一个等腰三角形一定不是等腰三角形 D. 一个等腰三角形一定不是钝角三角形
6.一个三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是( )
A. 2 B. 3 C. 4 D. 8
7.下列长度的三条线段能组成三角形的是( )
A. 1,2,3 B. 2,2,4 C. 3,4,5 D. 3,4,8
8.下列各组数据能作为一个等腰三角形各边长的是( )
A. 1,1,2 B. 4,2,4 C. 2,3,4 D. 3,3,7
9.如图,三角形被木板遮住一部分,这个三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 以上都有可能
10.如图1为图2中三角柱ABCEFG的展开图,其中AE、BF、CG、DH是三角柱的边.若图1中,AD=10,CD=2,则下列何者可为AB长度?( )
A. 2 B. 3 C. 4 D. 5
二、填空题
11.如图,∠C在三角形中所对的边是________________.
12.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有________对
13.用7根火柴首尾顺次相接摆成一个三角形,能摆成_______个不同的三角形.
14.过A、B、C、D、E五个点中任意三点画三角形;
(1)其中以AB为一边可以画出__________个三角形;
(2)其中以C为顶点可以画出 __________个三角形.
15.15.等腰三角形的两边长分别为3和5,则它的周长为__________。
16.如图,在图1中互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个……则在第n个图形中,互不重叠的三角形共有__________个(用含n的代数式表示).
17.如图,图1中共有3个三角形,图2中共有6个三角形,图3中共有10个三角形,…,以此类推,则图6中共有 __________ 个三角形.
18.平面上有5个点,其中任意三点都不在同一条直线上,则这些点共可组成__________个不同的三角形.
三、解答题
19.一个三角形三边长之比为2:3:4,周长为36cm,求此三角形的三边长.
20.a,b,c分别为△ABC的三边,且满足a+b=3c﹣2,a﹣b=2c﹣6.
(1)求c的取值范围;
(2)若△ABC的周长为18,求c的值.
参考答案
1.C
【解析】∵由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形,
∴C符合三角形的概念.
故选C.
2.B
【解析】试题分析:根据三角形的第三边大于两边之差,而小于两边之和求得第三边的取值范围,再进一步选择.
解:根据三角形的三边关系,得
第三边大于:8﹣3=5,而小于:3+8=11.
则此三角形的第三边可能是:10.
故选:B.
点评:本题考查了三角形的三边关系,即三角形的第三边大于两边之差,而小于两边之和,此题基础题,比较简单.
3.B
【解析】试题解析:因为三角形的定义是:由不在同一条直线上的三条线段首尾顺次相接所成的图形.
故选B.
4.B
【解析】∵|m n|+(n p)2=0,
∴m n=0,n p=0,
∴m=n,n=p,
∴m=n=p,
∴△ABC为等边三角形。
故选B.
点睛:本题可根据非负数的性质“两个非负数相加,和为0,这两个非负数的值都为0.”得出m、n、p的关系,再判断三角形的类型.
5.D
【解析】A、如等腰直角三角形,既是直角三角形,也是等腰三角形,故该选项错误;
B、如等边三角形,既是等腰三角形,也是锐角三角形,故该选项错误;
C、如顶角是120°的等腰三角形,是钝角三角形,也是等腰三角形,故该选项错误;
D、一个等边三角形的三个角都是60°,故该选项正确.
故选D.
6.C
【解析】试题分析:由三角形的三边关系可得5-3<第三边长<3+5,即2<第三边长<8,又因第三边长是偶数,所以第三边长可为4,6,故答案选C.
考点:三角形的三边关系.
7.C
【解析】试题分析:根据三角形的三边满足两边之和大于第三边来进行判断.
解:A、1+2=3,不能构成三角形,故A错误;
B、2+2=4,不能构成三角形,故B错误;
C、3+4>5,能构成三角形,故C正确;
D、3+4<8,不能构成三角形,故D错误.
故选C.
考点:三角形三边关系.
8.B
【解析】A选项:因为1+1=2,所以本组数据不可以构成等腰三角形;故本选项错误;
B选项:因为4﹣4<2<4+4,所以本组数据可以构成等腰三角形;故本选项正确;
C选项:因为这个三角形没有一组相等的边,所以构不成等腰三角形;故本选项错误;
D选项:因为3+3<7,所以本组数据不可以构成等腰三角形;故本选项错误;
故选B.
9.D
【解析】从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角,
故选D.
10.C
【解析】由图可知,AD=AB+BC+CD,
∵AD=10,CD=2,
∴AB+BC=8,
设AB=x,则BC=8 x,
所以 ,
解不等式①得x>3,
解不等式②得,x<5,
所以,不等式组的解集是3
故选C.
点睛:根据图形先求出AB与BC的和,然后设AB=x,表示出BC=8-x,然后利用三角形的任意两边之和大于第三边,两边之差小于第三边列出不等式组,求解得到AB的取值范围,即可得解.
11.AE,BD,AB
【解析】在△ABC中, ∠C的对边是AB; 在△ACE中, ∠C的对边是AE在△BCD中, ∠C的对边是BD;
故答案为: AE,BD,AB
12.3
【解析】图中以BC为公共边的”共边三角形”有△ABC,△DBC,△EBC,共3对.故选B.
13.2
【解析】用7根火柴首尾顺次相接摆成一个三角形,可以摆出两个不同的等腰三角形,
即边长分别为:3,3,1;2,2,3两种三角形.
故本题答案为:2.
14.(1)3(2)6
【解析】试题分析:
(1)根据三角形定义,再选择一个点,然后顺次连接即可画出图形;
(2)根据三角形的定义,再A、B、D、E中任意选择两个点,然后顺次连接即可画出图形.
(1)如图,以AB为一边的三角形有△ABC、△ABD、△ABE共3个;
(2)如图,以点C为顶点的三角形有△ABC、△BEC、△BCD、△ACE、△ACD、△CDE共6个.
故答案为:(1)3,(2)6.
15.11或13
【解析】试题分析:题目给出等腰三角形有两条边长为3和5,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解:有两种情况:①腰长为3,底边长为5,三边为:3,3,5可构成三角形,周长=3+3+5=11;
②腰长为5,底边长为3,三边为:5,5,3可构成三角形,周长=5+5+3=13.
故答案为:11或13.
考点:三角形三边关系;等腰三角形的性质.
16.(3n+1)
【解析】试题分析:观察图形可得,第1个图形中,互不重叠的三角形共有4个,第2个图形中,互不重叠的三角形共有4+3=7个,第3个图形中,互不重叠的三角形共有4+3×2=10个,…根据这个规律可得在第n个图形中,互不重叠的三角形共有4+3(n﹣1)=3n+1.
考点:规律探究题.
17.28
【解析】解:由已知通过观察得:
图1有: 个三角形,
图2有: 个三角形,
图3有: 个三角形,
所以图6中共有: 个三角形,
故答案为:28.
18.10
【解析】解:∵平面上有5个点,其中任意三点都不在同一条直线上,
∴这些点共可组成5×(5-1)÷2=10个不同的三角形.
点睛:数三角形的个数,可以按照数线段条数的方法,如果平面上有5个点,其中任意三点都不在同一条直线上,那么就有 条线段,得到个三角形.
19.8cm,12cm,16cm.
【解析】试题分析:设三边长分别为2x,3x,4x,根据周长为36cm,可得出方程,解出即可.
设三边长分别为2x,3x,4x,
由题意得,2x+3x+4x=36,
解得:x=4.
故三边长为:8cm,12cm,16cm.
点睛:本题考查了一元一次方程的几何应用及见比设参的数学思想, 因为角形三边长之比为2:3:4,所以可设三边长分别为2x,3x,4x,根据周长为36cm,可得出方程求解即可.
20.(1)1<c<6(2)c=5
【解析】【试题分析】(1)利用三角形两边之和大于第三边,两边之差小于第三边,得不等式组解得1
【试题解析】
(1)由题意得解得1
(2)由题意得3c-2+c=18,解得c=5.
【方法点睛】本题目涉及三角形的边的综合题,将三角形的三边关系与不等式组、方程三者巧妙的结合起来.实属难得,但难度不大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
