11.1.2 三角形的角平分线、中线和高同步作业
文档属性
| 名称 | 11.1.2 三角形的角平分线、中线和高同步作业 |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-11 10:58:04 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
11.1.2三角形的角平分线、中线和高同步作业
姓名:__________班级:__________考号:__________
一、选择题
1.画△ABC的边AB上的高,下列画法中,正确的是( )
2.下列说法错误的是( )
A.三角形的三条高一定在三角形内部交于一点
B.三角形的三条中线一定在三角形内部交于一点
C.三角形的三条角平分线一定在三角形内部交于一点
D.三角形的三条高可能相交于外部一点
3.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定
4.能把一个三角形的面积一分为二的线段是( )
A. 高 B. 中线 C. 角平分线 D. 外角平分线
5.下列说法不正确的是( )
A. △ABC的中线AD平分边BC
B. △ABC的角平分线BE平分∠ABC
C. △ABC的高CF垂直AB
D. 直角△ABC只有一条高
6.如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
A. AB=2BF B. ∠ACE=∠ACB C. AE=BE D. CD⊥BE
7.如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )
A. △ABC中,AD是边BC上的高 B. △ABC中,GC是边BC上的高
C. △GBC中,GC是边BC上的高 D. △GBC中,CF是边BG上的高
8.如图,∠1=∠2,∠3=∠4,则下列结论正确的有( )
①AD平分∠BAE;②AF平分∠EAC;③AE平分∠DAF;④AF平分∠BAC;⑤AE平分∠BAC.
A. 4个 B. 3个 C. 2个 D. 1个
9.给出下列说法:①三条线段组成的图形叫三角形;②三角形的角平分线是射线;③三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外;④任何一个三角形都有三条高、三条中线、三条角平分线;⑤三角形的三条角平分线交于一点,且这点在三角形内.正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
10.如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
A. 1cm2 B. 2cm2 C. 8cm2 D. 16cm2
二、填空题
11.如图,AD⊥BC于D,那么图中以AD为高的三角形有______个.
12.如图,在△ABC中,BD=CD,∠ABE=∠CBE,BE交AD于点F.
(1)______是△ABC的角平分线;
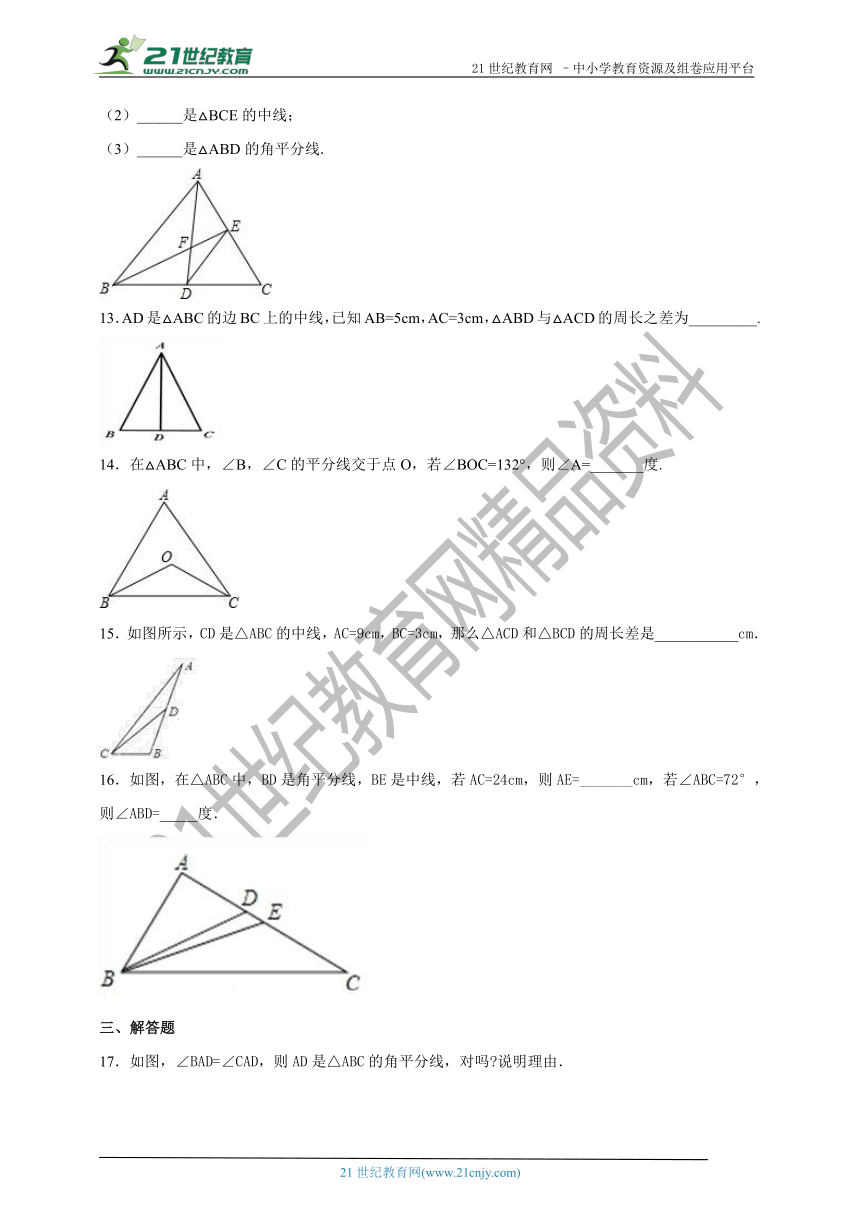
(2)______是△BCE的中线;
(3)______是△ABD的角平分线.
13.AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,△ABD与△ACD的周长之差为_________.
14.在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132°,则∠A=_______度.
15.如图所示,CD是△ABC的中线,AC=9cm,BC=3cm,那么△ACD和△BCD的周长差是___________cm.
16.如图,在△ABC中,BD是角平分线,BE是中线,若AC=24cm,则AE=_______cm,若∠ABC=72°,则∠ABD=_____度.
三、解答题
17.如图,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗 说明理由.
18.已知:△ABC中,AB=AC,BD是AC边上的中线,如果D点把三角形ABC的周长分为12cm和15cm两部分,求此三角形各边的长.
19.如图,AD为△ABC的中线,BE为△ABD的中线.若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
20.如图,△ABC是某村一遍若干亩土地的示意图,在党的“十六大”精神的指导下,为进一步加大农村经济结构调整的力度,某村决定把这块土地平均分给四位“花农”种植,请你帮他们分一分,提供两种分法.要求:画出图形,并简要说明分法.
21.如图,AD是∠CAB的角平分线,DE∥AB,DF∥AC,EF交AD于点O.请问:DO是∠EDF的角平分线吗?如果是,请给予证明;如果不是,请说明理由.
参考答案
1.D
【解析】试题分析:三角形的高即从三角形的顶点向对边引垂线,顶点和垂足间的线段.根据概念可知.
解:过点C作边AB的垂线段,即画AB边上的高CD,所以画法正确的是D.
故选:D.
考点:三角形的角平分线、中线和高.
2.A.
【解析】
试题分析:A.三角形的三条高一定在三角形内部交于一点 ,错误,符合题意;
B.三角形的三条中线一定在三角形内部交于一点,正确,不符合题意;
C.三角形的三条角平分线一定在三角形内部交于一点,正确,不符合题意;
D.三角形的三条高可能相交于外部一点,正确,不符合题意.
故选A.
考点: 命题与定理.
3.B
【解析】试题分析:因为直角三角形的三条高线的交点是直角顶点,而其他三角形三条高线的交点都不在顶点上,所以如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是直角三角形.
故选B.
点睛:本题考查的是三角形高的性质,熟知直角三角形的三条高的交点恰好是三角形的一个顶点是解答此题的关键.
4.B
【解析】试题分析:三角形的中线把三角形分成两个三角形,这两个三角形等底同高,所以这两个三角形的面积相等,所以能把一个三角形的面积一分为二的线段是中线.
故选:B.
5.D
【解析】试题分析:A、∵AD是△ABC的中线,∴D是BC的中点,即AD平分边BC,故此选项正确;
B、∵BE是△ABC的角平分线,∴BE平分∠ABC,故此选项正确;
C、∵CF是△ABC的高,∴CF⊥AB,故此选项正确;
D、直角△ABC有三条高,其中两条是直角边,一条在三角形内部,故此选项错误.
故选D.
6.C
【解析】试题分析:
∵CD,CE,CF分别是△ABC的高、角平分线、中线
∴CD⊥BE,∠ACE=∠ACB ,AB="2BF"
故选B
7.B
【解析】试题分析:A、AD经过△ABC的一个顶点,且AD垂直于BC边所在的直线,所以△ABC中AD是边BC上的高,故此选项正确;
B、GC没有经过BC所对的顶点A,所以△ABC中,GC不是BC边上的高,故此选项错误;
C、GC经过△GBC的一个顶点,且GC垂直于BC,所以△GBC中GC是边BC上的高,故此选项正确;
D、CF经过△GBC的一个顶点,且CF垂直于BG,所以△GBC中CF是边BG上的高,故此选项正确.
故选B.
点睛:本题主要考查了三角形高的概念,应熟记三角形的高应具备的两个条件:①经过三角形的一个顶点,②垂直于这个顶点的对边.
8.C
【解析】试题解析:AD不一定平分∠BAF,①错误;
AF不一定平分∠DAC,②错误;
∵∠1=∠2,∴AE平分∠DAF,③正确;
∵∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4,即∠BAE=∠CAE,
∴AE平分∠BAC,④正确;
故选C.
9.B
【解析】试题分析:三条线段首尾顺次相接组成的图形叫三角形,故①错误;
三角形的角平分线是线段,故②错误;
三角形的高所在的直线交于一点,这一点可以是三角形的直角顶点,故③错误;
所以正确的命题是④⑤,共2个.
故选B.
10.D
【解析】试题分析:∵F是CE中点,
∴△BEF的面积与△BCF的面积相等,
∴S△BEC=2S△BEF=8(cm2),
∵D、E分别为BC、AD的中点,
∴△ABE、△DBE、△DCE、△AEC的面积相等,
∴S△ABC=2S△BEC=16(cm2).
故选D.
点睛:此题考查了三角形的中线,根据三角形中线将三角形的面积分成相等的两部分是解题的关键.
11.6
【解析】试题分析:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有△ABD、△ABE、△ABC、△ADE、△ADC、△AEC,共6个,
∴以AD为高的三角形有6个.
故答案为:6.
点睛:此题主要考查了三角形的高,三角形的高可以在三角形外,也可以在三角形内,所以确定三角形的高比较灵活.
12. BE, DE, BF
【解析】试题分析:(1)∵∠ABE=∠CBE ,∴BE是△ABC的角平分线;
(2)∵BD=CD,∴DE是△BCE的中线;
(3)∵∠ABE=∠CBE ,∴BF是△ABD的角平分线.
故答案为:(1)BE,(2)DE,(3)BF.
13.2cm
【解析】试题分析:∵AD是△ABC中BC边上的中线,
∴BD=DC=BC,
∴△ABD和△ADC的周长的差
=(AB+BC+AD)-(AC+BC+AD)
=AB-AC
=5-3
=2(cm).
故答案为:2cm.
14.84
【解析】试题分析:∵∠BOC=132°,
∴∠OBC+∠OCB=48°,
∵∠ABC与∠ACB的平分线相交于O点,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=96°,
∴∠A=180°-96°=84°.
故答案为:84.
点睛:本题考查了三角形的角平分线概念和三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
15.6
【解析】∵CD是△ABC的中线,
∴AD=BD.
∵C△ACD=AC+AD+CD,C△BCD=BC+BD+CD,
∴C△ACD-C△BCD
=(AC+AD+CD-(BC+BD+CD)=AC+AD+CD-BC-BD-CD=AC-BC=9-3=6(cm).
点睛:由三角形一边上的中线把三角形分成的两个新三角形的周长差等于原三角形中另外两边的差.
16.12,36
【解析】∵在△ABC中,BD是角平分线,BE是中线,
∴AE=AC=12(cm),∠ABD=∠ABC=36°.
17.不是,理由见解析.
【解析】试题分析:考查了三角形的角平分线的定义,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
试题解析:根据三角形的角平分线的定义,可知:①平分三角形的一个内角;②是一条线段,一个端点是三角形的顶点,另一点在这个顶点的对边上.而此题中AD满足①,但点D不在BC边上,故不满足②.所以,AD不是△ABC的角平分线.
18.8厘米,8厘米,11厘米或10厘米,10厘米,7厘米
【解析】试题分析:本题D点把三角形ABC的周长分成两部分(AB+AD)和(BC+CD),题中未说明12cm和15cm分别是哪一部分,因此要分类讨论.
试题解析:
∵AB=AC,BD是AC边上的中线,
∴AB=2AD=2CD,
∴AB+AD=3AD.
①当AB与AD的和是12厘米时,
AD=12÷3=4(厘米),
所以AB=AC=2×4=8(厘米),
BC=12+15-8×2=12+15-16=11(厘米);
②当AB与AD的和是15厘米时,
AD=15÷3=5(厘米),
所以AB=AC=2×5=10(厘米),
BC=12+15-10×2=12+15-20=7(厘米).
所以三角形的三边可能是8厘米,8厘米,11厘米或10厘米,10厘米,7厘米.
点睛:此题考查了等腰三角形的概念、中线的性质.此题难度适中,注意掌握方程思想、分类讨论思想与数形结合思想的应用.
19.4
【解析】试题分析:首先根据三角形的中线把三角形的面积分成相等的两部分可得△EBD的面积是10,再利用三角形的面积公式进而得到BD边上的高.
试题解析:∵AD为△ABC的中线,BE为△ABD的中线,
∴S△ABD=S△ABC,S△BDE=S△ABD,
∴S△BDE=×S△ABC=S△ABC,
∵△ABC的面积为40,
∴S△BDE=×40=10,
设△BDE中BD边上的高为x,
∵BD=5,
∴×5 x=10,
解得x=4,
故△BDE中BD边上的高为4.
20.图形见解析
【解析】试题分析:根据题意,就是要将△ABC分为四等份,即面积相等的四份,一种是取三边的中点,两两相连,并与三角形的另一个顶点和其对边上的中点相连,所得的四个三角形的面积互相相等;另一种,在一边上取四等分点,分别连接这条边对应的顶点和这三个点,可以知道四个三角形等底同高,故面积相等.
第一种是取各边的中点,分别取,AB.BC,AC的中点D,E,Y,连接DE,EY和AE,所形成的四个三角形面积相等(如下图).
第二种,在BC边上取四等分点D,E,F,分别连接AD,AE,AF,所形成的四个三角形面积相等(如下图).
21.是,理由见解析
【解析】试题分析:
由DE∥AB,DF∥AC,可得∠EDA=∠DAF,∠FDA=∠EAD,再结合∠EAD=∠FAD,就可得∠EDA=∠FDA,从而得到DO平分∠EDF.
试题解析:
DO是∠EDF的角平分线,理由如下:
∵AD是∠CAB的角平分线,
∴∠EAD=∠FAD.
∵DE∥AB,DF∥AC,
∴∠EDA=∠FAD,∠FDA=∠EAD.
∴∠EDA=∠FDA,
∴DO是∠EDF的角平分线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
11.1.2三角形的角平分线、中线和高同步作业
姓名:__________班级:__________考号:__________
一、选择题
1.画△ABC的边AB上的高,下列画法中,正确的是( )
2.下列说法错误的是( )
A.三角形的三条高一定在三角形内部交于一点
B.三角形的三条中线一定在三角形内部交于一点
C.三角形的三条角平分线一定在三角形内部交于一点
D.三角形的三条高可能相交于外部一点
3.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定
4.能把一个三角形的面积一分为二的线段是( )
A. 高 B. 中线 C. 角平分线 D. 外角平分线
5.下列说法不正确的是( )
A. △ABC的中线AD平分边BC
B. △ABC的角平分线BE平分∠ABC
C. △ABC的高CF垂直AB
D. 直角△ABC只有一条高
6.如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
A. AB=2BF B. ∠ACE=∠ACB C. AE=BE D. CD⊥BE
7.如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )
A. △ABC中,AD是边BC上的高 B. △ABC中,GC是边BC上的高
C. △GBC中,GC是边BC上的高 D. △GBC中,CF是边BG上的高
8.如图,∠1=∠2,∠3=∠4,则下列结论正确的有( )
①AD平分∠BAE;②AF平分∠EAC;③AE平分∠DAF;④AF平分∠BAC;⑤AE平分∠BAC.
A. 4个 B. 3个 C. 2个 D. 1个
9.给出下列说法:①三条线段组成的图形叫三角形;②三角形的角平分线是射线;③三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外;④任何一个三角形都有三条高、三条中线、三条角平分线;⑤三角形的三条角平分线交于一点,且这点在三角形内.正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
10.如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
A. 1cm2 B. 2cm2 C. 8cm2 D. 16cm2
二、填空题
11.如图,AD⊥BC于D,那么图中以AD为高的三角形有______个.
12.如图,在△ABC中,BD=CD,∠ABE=∠CBE,BE交AD于点F.
(1)______是△ABC的角平分线;
(2)______是△BCE的中线;
(3)______是△ABD的角平分线.
13.AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,△ABD与△ACD的周长之差为_________.
14.在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132°,则∠A=_______度.
15.如图所示,CD是△ABC的中线,AC=9cm,BC=3cm,那么△ACD和△BCD的周长差是___________cm.
16.如图,在△ABC中,BD是角平分线,BE是中线,若AC=24cm,则AE=_______cm,若∠ABC=72°,则∠ABD=_____度.
三、解答题
17.如图,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗 说明理由.
18.已知:△ABC中,AB=AC,BD是AC边上的中线,如果D点把三角形ABC的周长分为12cm和15cm两部分,求此三角形各边的长.
19.如图,AD为△ABC的中线,BE为△ABD的中线.若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
20.如图,△ABC是某村一遍若干亩土地的示意图,在党的“十六大”精神的指导下,为进一步加大农村经济结构调整的力度,某村决定把这块土地平均分给四位“花农”种植,请你帮他们分一分,提供两种分法.要求:画出图形,并简要说明分法.
21.如图,AD是∠CAB的角平分线,DE∥AB,DF∥AC,EF交AD于点O.请问:DO是∠EDF的角平分线吗?如果是,请给予证明;如果不是,请说明理由.
参考答案
1.D
【解析】试题分析:三角形的高即从三角形的顶点向对边引垂线,顶点和垂足间的线段.根据概念可知.
解:过点C作边AB的垂线段,即画AB边上的高CD,所以画法正确的是D.
故选:D.
考点:三角形的角平分线、中线和高.
2.A.
【解析】
试题分析:A.三角形的三条高一定在三角形内部交于一点 ,错误,符合题意;
B.三角形的三条中线一定在三角形内部交于一点,正确,不符合题意;
C.三角形的三条角平分线一定在三角形内部交于一点,正确,不符合题意;
D.三角形的三条高可能相交于外部一点,正确,不符合题意.
故选A.
考点: 命题与定理.
3.B
【解析】试题分析:因为直角三角形的三条高线的交点是直角顶点,而其他三角形三条高线的交点都不在顶点上,所以如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是直角三角形.
故选B.
点睛:本题考查的是三角形高的性质,熟知直角三角形的三条高的交点恰好是三角形的一个顶点是解答此题的关键.
4.B
【解析】试题分析:三角形的中线把三角形分成两个三角形,这两个三角形等底同高,所以这两个三角形的面积相等,所以能把一个三角形的面积一分为二的线段是中线.
故选:B.
5.D
【解析】试题分析:A、∵AD是△ABC的中线,∴D是BC的中点,即AD平分边BC,故此选项正确;
B、∵BE是△ABC的角平分线,∴BE平分∠ABC,故此选项正确;
C、∵CF是△ABC的高,∴CF⊥AB,故此选项正确;
D、直角△ABC有三条高,其中两条是直角边,一条在三角形内部,故此选项错误.
故选D.
6.C
【解析】试题分析:
∵CD,CE,CF分别是△ABC的高、角平分线、中线
∴CD⊥BE,∠ACE=∠ACB ,AB="2BF"
故选B
7.B
【解析】试题分析:A、AD经过△ABC的一个顶点,且AD垂直于BC边所在的直线,所以△ABC中AD是边BC上的高,故此选项正确;
B、GC没有经过BC所对的顶点A,所以△ABC中,GC不是BC边上的高,故此选项错误;
C、GC经过△GBC的一个顶点,且GC垂直于BC,所以△GBC中GC是边BC上的高,故此选项正确;
D、CF经过△GBC的一个顶点,且CF垂直于BG,所以△GBC中CF是边BG上的高,故此选项正确.
故选B.
点睛:本题主要考查了三角形高的概念,应熟记三角形的高应具备的两个条件:①经过三角形的一个顶点,②垂直于这个顶点的对边.
8.C
【解析】试题解析:AD不一定平分∠BAF,①错误;
AF不一定平分∠DAC,②错误;
∵∠1=∠2,∴AE平分∠DAF,③正确;
∵∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4,即∠BAE=∠CAE,
∴AE平分∠BAC,④正确;
故选C.
9.B
【解析】试题分析:三条线段首尾顺次相接组成的图形叫三角形,故①错误;
三角形的角平分线是线段,故②错误;
三角形的高所在的直线交于一点,这一点可以是三角形的直角顶点,故③错误;
所以正确的命题是④⑤,共2个.
故选B.
10.D
【解析】试题分析:∵F是CE中点,
∴△BEF的面积与△BCF的面积相等,
∴S△BEC=2S△BEF=8(cm2),
∵D、E分别为BC、AD的中点,
∴△ABE、△DBE、△DCE、△AEC的面积相等,
∴S△ABC=2S△BEC=16(cm2).
故选D.
点睛:此题考查了三角形的中线,根据三角形中线将三角形的面积分成相等的两部分是解题的关键.
11.6
【解析】试题分析:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有△ABD、△ABE、△ABC、△ADE、△ADC、△AEC,共6个,
∴以AD为高的三角形有6个.
故答案为:6.
点睛:此题主要考查了三角形的高,三角形的高可以在三角形外,也可以在三角形内,所以确定三角形的高比较灵活.
12. BE, DE, BF
【解析】试题分析:(1)∵∠ABE=∠CBE ,∴BE是△ABC的角平分线;
(2)∵BD=CD,∴DE是△BCE的中线;
(3)∵∠ABE=∠CBE ,∴BF是△ABD的角平分线.
故答案为:(1)BE,(2)DE,(3)BF.
13.2cm
【解析】试题分析:∵AD是△ABC中BC边上的中线,
∴BD=DC=BC,
∴△ABD和△ADC的周长的差
=(AB+BC+AD)-(AC+BC+AD)
=AB-AC
=5-3
=2(cm).
故答案为:2cm.
14.84
【解析】试题分析:∵∠BOC=132°,
∴∠OBC+∠OCB=48°,
∵∠ABC与∠ACB的平分线相交于O点,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=96°,
∴∠A=180°-96°=84°.
故答案为:84.
点睛:本题考查了三角形的角平分线概念和三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
15.6
【解析】∵CD是△ABC的中线,
∴AD=BD.
∵C△ACD=AC+AD+CD,C△BCD=BC+BD+CD,
∴C△ACD-C△BCD
=(AC+AD+CD-(BC+BD+CD)=AC+AD+CD-BC-BD-CD=AC-BC=9-3=6(cm).
点睛:由三角形一边上的中线把三角形分成的两个新三角形的周长差等于原三角形中另外两边的差.
16.12,36
【解析】∵在△ABC中,BD是角平分线,BE是中线,
∴AE=AC=12(cm),∠ABD=∠ABC=36°.
17.不是,理由见解析.
【解析】试题分析:考查了三角形的角平分线的定义,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
试题解析:根据三角形的角平分线的定义,可知:①平分三角形的一个内角;②是一条线段,一个端点是三角形的顶点,另一点在这个顶点的对边上.而此题中AD满足①,但点D不在BC边上,故不满足②.所以,AD不是△ABC的角平分线.
18.8厘米,8厘米,11厘米或10厘米,10厘米,7厘米
【解析】试题分析:本题D点把三角形ABC的周长分成两部分(AB+AD)和(BC+CD),题中未说明12cm和15cm分别是哪一部分,因此要分类讨论.
试题解析:
∵AB=AC,BD是AC边上的中线,
∴AB=2AD=2CD,
∴AB+AD=3AD.
①当AB与AD的和是12厘米时,
AD=12÷3=4(厘米),
所以AB=AC=2×4=8(厘米),
BC=12+15-8×2=12+15-16=11(厘米);
②当AB与AD的和是15厘米时,
AD=15÷3=5(厘米),
所以AB=AC=2×5=10(厘米),
BC=12+15-10×2=12+15-20=7(厘米).
所以三角形的三边可能是8厘米,8厘米,11厘米或10厘米,10厘米,7厘米.
点睛:此题考查了等腰三角形的概念、中线的性质.此题难度适中,注意掌握方程思想、分类讨论思想与数形结合思想的应用.
19.4
【解析】试题分析:首先根据三角形的中线把三角形的面积分成相等的两部分可得△EBD的面积是10,再利用三角形的面积公式进而得到BD边上的高.
试题解析:∵AD为△ABC的中线,BE为△ABD的中线,
∴S△ABD=S△ABC,S△BDE=S△ABD,
∴S△BDE=×S△ABC=S△ABC,
∵△ABC的面积为40,
∴S△BDE=×40=10,
设△BDE中BD边上的高为x,
∵BD=5,
∴×5 x=10,
解得x=4,
故△BDE中BD边上的高为4.
20.图形见解析
【解析】试题分析:根据题意,就是要将△ABC分为四等份,即面积相等的四份,一种是取三边的中点,两两相连,并与三角形的另一个顶点和其对边上的中点相连,所得的四个三角形的面积互相相等;另一种,在一边上取四等分点,分别连接这条边对应的顶点和这三个点,可以知道四个三角形等底同高,故面积相等.
第一种是取各边的中点,分别取,AB.BC,AC的中点D,E,Y,连接DE,EY和AE,所形成的四个三角形面积相等(如下图).
第二种,在BC边上取四等分点D,E,F,分别连接AD,AE,AF,所形成的四个三角形面积相等(如下图).
21.是,理由见解析
【解析】试题分析:
由DE∥AB,DF∥AC,可得∠EDA=∠DAF,∠FDA=∠EAD,再结合∠EAD=∠FAD,就可得∠EDA=∠FDA,从而得到DO平分∠EDF.
试题解析:
DO是∠EDF的角平分线,理由如下:
∵AD是∠CAB的角平分线,
∴∠EAD=∠FAD.
∵DE∥AB,DF∥AC,
∴∠EDA=∠FAD,∠FDA=∠EAD.
∴∠EDA=∠FDA,
∴DO是∠EDF的角平分线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
