北师大版数学六下总复习-正比例和反比例课件
文档属性
| 名称 | 北师大版数学六下总复习-正比例和反比例课件 |  | |
| 格式 | zip | ||
| 文件大小 | 287.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-11 20:01:25 | ||
图片预览











文档简介
课件33张PPT。北师大版六年级下册总复习正比例与反比例回顾交流知识总结基础练习提升练习课堂小结举例说明什么是比,什么是比例,以及它们的应用。1.比的意义:两个数相除又叫作两个数的比。如:
3÷5=3∶5。
2.比的意义的应用:应用比的意义可以求比值,用比
的前项除以比的后项,所得到的结果就是比值,比
值可以是分数、小数或整数。如:3∶5=3÷5=35
(或0.6)。
3.比的基本性质:比的前项和后项同时乘或除以相同
的数(0除外),比值不变。回顾交流4.比的基本性质的应用:应用比的基本性质可以化简比,
把比的前项和后项同时乘或除以相同的数(0除外),
使比的前项和后项只有公因数1。
如:8∶12=(8÷4)∶(12÷4)=2∶3。
5.比例的意义:表示两个比相等的式子叫作比例。
如:3∶5=6∶10。
6.比例的意义的应用:判断两个比能否组成比例。如:
因为1∶5=15,2∶10=15,所以1∶5和2∶10能组成
比例:1∶5=2∶10。7.比例的基本性质:一个比例中,两个外项的积等于两
个内项的积。如:比例3∶5=6∶10中,3×10=5×6。
8.比例的基本性质的应用:应用比例的基本性质可以判
断两个比能否组成比例,还可以解比例。
如:x∶5=3∶6
解: 6x=3×5
x=15÷6
x=2.5填一填,并说一说比、分数、除法之间的联系。3355aabb1.比例尺的意义:一幅图的图上距离和实际距离的比,
叫作这幅图的比例尺,
图上距离∶实际距离=比例尺。
2.比例尺的分类:数值比例尺,如:1∶6000。
线段比例尺,如:
3.已知比例尺和实际距离,求图上距离的方法:
实际距离×比例尺=图上距离;
已知比例尺和图上距离,求实际距离的方法:
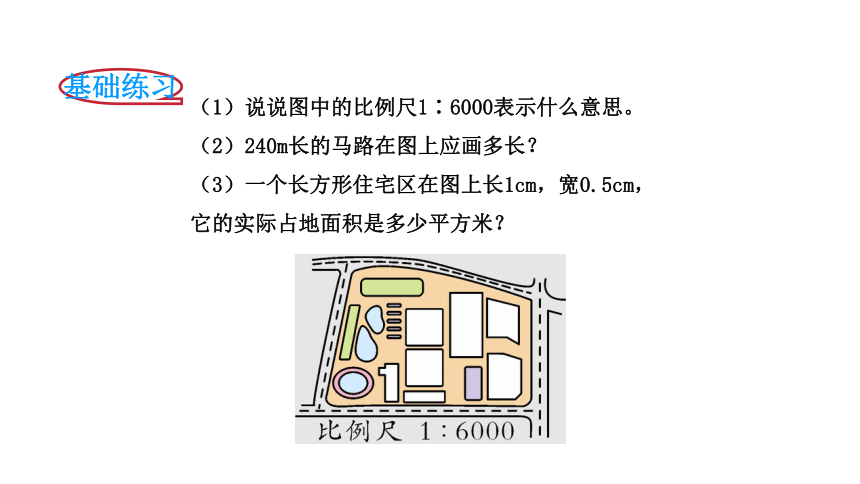
图上距离÷比例尺=实际距离。(1)说说图中的比例尺1∶6000表示什么意思。
(2)240m长的马路在图上应画多长?
(3)一个长方形住宅区在图上长1cm,宽0.5cm,它的实际占地面积是多少平方米?基础练习4.解答
(1)图中的比例尺1∶6000表示图上1cm相当于实
际的60m。
(2)240m=24000cm 24000÷6000=4(cm)
答:240m长的马路在图上应画4cm。
(3)长:6000cm=60m
宽:0.5×6000=3000(cm) 3000cm=30m
面积:60×30=1800(m2)
答:它的实际占地面积是1800平方米。举例说说生活中有哪些成正比例的量,
有哪些成反比例的量。 正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用以下关系式表示:x/y=k(一定)。
例如:正方形的周长与边长是成正比例的两个量;圆柱的底面积一定,圆柱的体积和高是成正比例的两个量;速度一定,路程和时间是成正比例的两个量。知识总结 反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量叫作成反比例的量,它们的关系叫作反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用以下关系式表示:xy=k(一定)。
例如:长方形的面积一定,它的长与宽是成反比例的两个量;圆柱的体积一定,圆柱的底面积与高是成反比例的两个量;路程一定,速度与时间是成反比例的两个量。 一辆汽车在高速路上行驶,速度保持在100千米/时,说一说汽车行驶的路程随时间变化的情况,并说说可以用哪些方式来表示这两个量之间的关系?200300400500(1)可以列表提升练习(2)可以画图 时间/分 路程/千米024351100500200400300(3)可以用式子表示如果用t表示汽车行驶的时间,
S表示汽车行驶的路程,那么 S÷t=100 你还能举出生活中或数学中一个量随另一个量变化的例子吗?正比例图像是一条什么线?反比例图像是一条什么线?0 2 3 4 5 6 7 1240 40 80120160200路程(千米)(1)(1)0 5 10 15 20 25 301202040 6080100加工时间(时)(2)(2)时间(时)每小时加工数(个)正比例图像反比例图像1.下面表格中的两个量是否成正比例或反比例? 为什么?(1)输液时一小瓶葡萄糖液均匀滴落时,每分滴数与所需时间的关系如下。每分滴数与所需时间成反比例60×20=1200, 50×24=120040×30=1200,30×40=1200(2)小明的身高与体重的关系如下小明的身高与体重不成比例100×40=4000,110×42=4620120÷43≈2.79130÷45≈2.89(3)体积一定,圆柱体的底面积和高的关系如下。体积一定,圆柱体的底面积和高成反比例300×2=600,200×3=600150×4=600,120×5=600,2.判断下面每题中的两个量是否成正比例或反比例。(1)出油率一定,香油质量与芝麻的质量.( ) (2)一捆100米长的电线,用去的长度与剩下的长度.( )
(3)三角形的面积一定,它的底和高( )
(4)一个数与它的倒数。 ( )
成正比例成反比例成反比例 不成比例出油率(一定)=香油质量÷芝麻的质量×100%三角形面积(一定)=底×高÷2a× =1 (a≠0) (用去的长度+剩下的长度=100米)时间/分 体积/升01020152551050204030603、右图表示的是一根水管不停地向水箱注水,水箱内水的体积的变化情况。16102623看图填表 4.磁悬浮列车匀速行驶时,路程与时间的关系如下。(1)图中的点A表示时间为1分时,磁悬浮列车驶过的路程为7千米。请你试着描出其它他各点. 时间/分路程/千米0243517351428214267A(2)连接各点,它们在一条直线上吗?时间/分 路程/千米0243517351428214267(3)列车运行2分半时,行驶的路程是多少?7×2.5=17.5(千米)时间/分0243516735211472842路程/千米一、填空。
1、在数量、单价和总价中:
(1)如果 一定, 和
成正比例。
(2)如果 一定, 和
成正比例。
(3)如果 一定, 和
成反比例 单价 总价
数量 总价 单价
数量
数量 总价
单价
2、已知 a × b=c。
(1)如果 一定, 和
成正比例。
(2)如果 一定, 和
成正比例。
(3)如果 一定, 和
成反比例 a b c b a
c
c a b
3、判断下面各数量关系中,当哪一个量一定时,另外两个量成什么比例?(1)时间、速度和路程
(2)工作总量、工作效率和工作时间
(3)单价、总价和数量
(4)平行四边形的面积、底和高4.判断下列各题(对的打“√”错的打“×”)(1)圆的周长与直径成正比例 。 ( )
圆的周长÷直径=π
(2)圆锥体的体积一定,它的底面积与高 成反比例。 ( )
圆锥体的体积= ×底面积×高
(3)圆柱体的侧面积一定,它的底面周长与高成反比例。 ( )
圆柱体的侧面积=底面周长×高
(4)y=8x,则y和x成反比例。 ( )
y÷x=8√√√×5.选择题(选择正确答案的序号填在括号里)(1)S表示路程,T表示时间,则S=60T中,S与T ( )
A、成正比例,B、成反比例,C、不成比例
(2)长方形的面积一定,它的长和宽( )
A、成正比例,B、成反比例,C、不成比例AB(3)比例尺一定,图上距离与实际距离 ( )
A、成正比例,B、成反比例,C、不成比例
(4)订《中国少年报》的份数与所需钱数( )
A、成正比例,B、成反比例,C、不成比例AA你学到了什么?课堂小结
3÷5=3∶5。
2.比的意义的应用:应用比的意义可以求比值,用比
的前项除以比的后项,所得到的结果就是比值,比
值可以是分数、小数或整数。如:3∶5=3÷5=35
(或0.6)。
3.比的基本性质:比的前项和后项同时乘或除以相同
的数(0除外),比值不变。回顾交流4.比的基本性质的应用:应用比的基本性质可以化简比,
把比的前项和后项同时乘或除以相同的数(0除外),
使比的前项和后项只有公因数1。
如:8∶12=(8÷4)∶(12÷4)=2∶3。
5.比例的意义:表示两个比相等的式子叫作比例。
如:3∶5=6∶10。
6.比例的意义的应用:判断两个比能否组成比例。如:
因为1∶5=15,2∶10=15,所以1∶5和2∶10能组成
比例:1∶5=2∶10。7.比例的基本性质:一个比例中,两个外项的积等于两
个内项的积。如:比例3∶5=6∶10中,3×10=5×6。
8.比例的基本性质的应用:应用比例的基本性质可以判
断两个比能否组成比例,还可以解比例。
如:x∶5=3∶6
解: 6x=3×5
x=15÷6
x=2.5填一填,并说一说比、分数、除法之间的联系。3355aabb1.比例尺的意义:一幅图的图上距离和实际距离的比,
叫作这幅图的比例尺,
图上距离∶实际距离=比例尺。
2.比例尺的分类:数值比例尺,如:1∶6000。
线段比例尺,如:
3.已知比例尺和实际距离,求图上距离的方法:
实际距离×比例尺=图上距离;
已知比例尺和图上距离,求实际距离的方法:
图上距离÷比例尺=实际距离。(1)说说图中的比例尺1∶6000表示什么意思。
(2)240m长的马路在图上应画多长?
(3)一个长方形住宅区在图上长1cm,宽0.5cm,它的实际占地面积是多少平方米?基础练习4.解答
(1)图中的比例尺1∶6000表示图上1cm相当于实
际的60m。
(2)240m=24000cm 24000÷6000=4(cm)
答:240m长的马路在图上应画4cm。
(3)长:6000cm=60m
宽:0.5×6000=3000(cm) 3000cm=30m
面积:60×30=1800(m2)
答:它的实际占地面积是1800平方米。举例说说生活中有哪些成正比例的量,
有哪些成反比例的量。 正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用以下关系式表示:x/y=k(一定)。
例如:正方形的周长与边长是成正比例的两个量;圆柱的底面积一定,圆柱的体积和高是成正比例的两个量;速度一定,路程和时间是成正比例的两个量。知识总结 反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量叫作成反比例的量,它们的关系叫作反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用以下关系式表示:xy=k(一定)。
例如:长方形的面积一定,它的长与宽是成反比例的两个量;圆柱的体积一定,圆柱的底面积与高是成反比例的两个量;路程一定,速度与时间是成反比例的两个量。 一辆汽车在高速路上行驶,速度保持在100千米/时,说一说汽车行驶的路程随时间变化的情况,并说说可以用哪些方式来表示这两个量之间的关系?200300400500(1)可以列表提升练习(2)可以画图 时间/分 路程/千米024351100500200400300(3)可以用式子表示如果用t表示汽车行驶的时间,
S表示汽车行驶的路程,那么 S÷t=100 你还能举出生活中或数学中一个量随另一个量变化的例子吗?正比例图像是一条什么线?反比例图像是一条什么线?0 2 3 4 5 6 7 1240 40 80120160200路程(千米)(1)(1)0 5 10 15 20 25 301202040 6080100加工时间(时)(2)(2)时间(时)每小时加工数(个)正比例图像反比例图像1.下面表格中的两个量是否成正比例或反比例? 为什么?(1)输液时一小瓶葡萄糖液均匀滴落时,每分滴数与所需时间的关系如下。每分滴数与所需时间成反比例60×20=1200, 50×24=120040×30=1200,30×40=1200(2)小明的身高与体重的关系如下小明的身高与体重不成比例100×40=4000,110×42=4620120÷43≈2.79130÷45≈2.89(3)体积一定,圆柱体的底面积和高的关系如下。体积一定,圆柱体的底面积和高成反比例300×2=600,200×3=600150×4=600,120×5=600,2.判断下面每题中的两个量是否成正比例或反比例。(1)出油率一定,香油质量与芝麻的质量.( ) (2)一捆100米长的电线,用去的长度与剩下的长度.( )
(3)三角形的面积一定,它的底和高( )
(4)一个数与它的倒数。 ( )
成正比例成反比例成反比例 不成比例出油率(一定)=香油质量÷芝麻的质量×100%三角形面积(一定)=底×高÷2a× =1 (a≠0) (用去的长度+剩下的长度=100米)时间/分 体积/升01020152551050204030603、右图表示的是一根水管不停地向水箱注水,水箱内水的体积的变化情况。16102623看图填表 4.磁悬浮列车匀速行驶时,路程与时间的关系如下。(1)图中的点A表示时间为1分时,磁悬浮列车驶过的路程为7千米。请你试着描出其它他各点. 时间/分路程/千米0243517351428214267A(2)连接各点,它们在一条直线上吗?时间/分 路程/千米0243517351428214267(3)列车运行2分半时,行驶的路程是多少?7×2.5=17.5(千米)时间/分0243516735211472842路程/千米一、填空。
1、在数量、单价和总价中:
(1)如果 一定, 和
成正比例。
(2)如果 一定, 和
成正比例。
(3)如果 一定, 和
成反比例 单价 总价
数量 总价 单价
数量
数量 总价
单价
2、已知 a × b=c。
(1)如果 一定, 和
成正比例。
(2)如果 一定, 和
成正比例。
(3)如果 一定, 和
成反比例 a b c b a
c
c a b
3、判断下面各数量关系中,当哪一个量一定时,另外两个量成什么比例?(1)时间、速度和路程
(2)工作总量、工作效率和工作时间
(3)单价、总价和数量
(4)平行四边形的面积、底和高4.判断下列各题(对的打“√”错的打“×”)(1)圆的周长与直径成正比例 。 ( )
圆的周长÷直径=π
(2)圆锥体的体积一定,它的底面积与高 成反比例。 ( )
圆锥体的体积= ×底面积×高
(3)圆柱体的侧面积一定,它的底面周长与高成反比例。 ( )
圆柱体的侧面积=底面周长×高
(4)y=8x,则y和x成反比例。 ( )
y÷x=8√√√×5.选择题(选择正确答案的序号填在括号里)(1)S表示路程,T表示时间,则S=60T中,S与T ( )
A、成正比例,B、成反比例,C、不成比例
(2)长方形的面积一定,它的长和宽( )
A、成正比例,B、成反比例,C、不成比例AB(3)比例尺一定,图上距离与实际距离 ( )
A、成正比例,B、成反比例,C、不成比例
(4)订《中国少年报》的份数与所需钱数( )
A、成正比例,B、成反比例,C、不成比例AA你学到了什么?课堂小结
