18.1.1 平行四边形的性质课件+教案
图片预览




文档简介
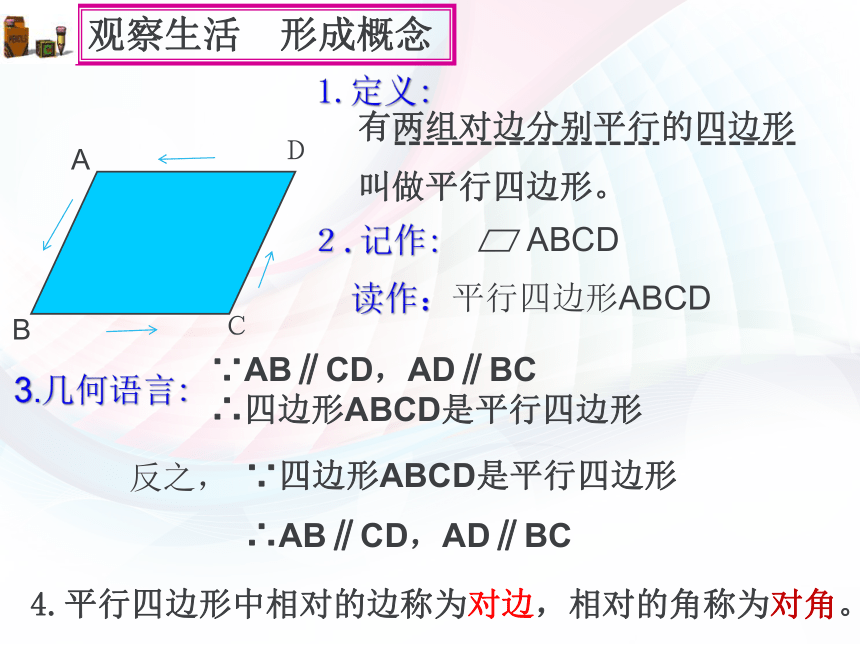
课件15张PPT。平行四边形及其性质(一)有两组对边分别平行的四边形 叫做平行四边形。2.记作:3.几何语言:∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BCABCD
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形读作:平行四边形ABCD4.平行四边形中相对的边称为对边,相对的角称为对角。1.定义:ABDC观察生活 形成概念 反之, 细心观察,猜想平行四边形的边、角之间有怎样的
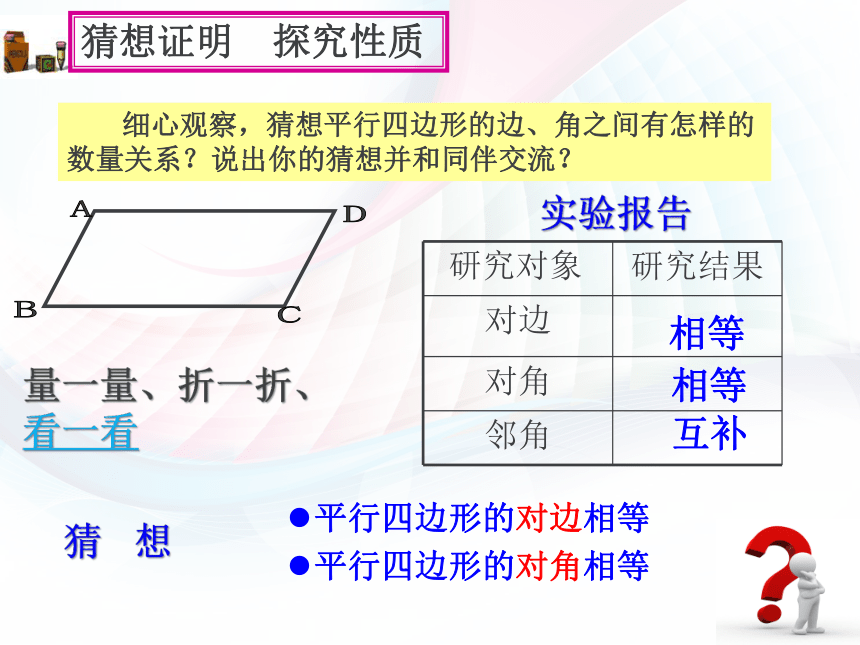
数量关系?说出你的猜想并和同伴交流? 猜想证明 探究性质 实验报告平行四边形的对边相等
平行四边形的对角相等
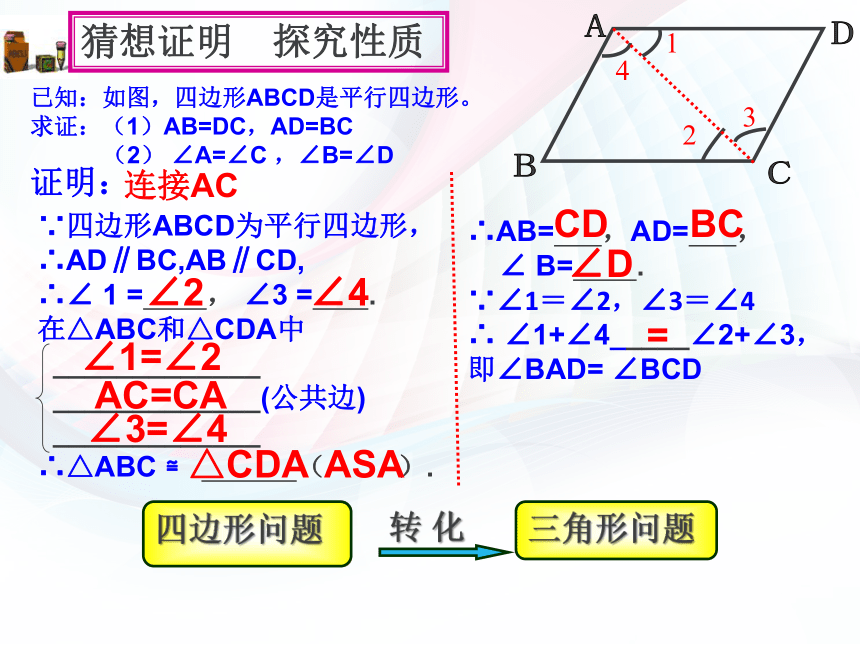
相等相等互补 猜 想量一量、折一折、看一看证明:连接AC
四边形问题三角形问题转 化猜想证明 探究性质 ∵四边形ABCD为平行四边形,
∴AD∥BC,AB∥CD,
∴∠ 1 = , ∠3 = .
在△ABC和△CDA中
_____________
_____________(公共边)
_____________
∴△ABC ≌ ( ).∠2∠4∠1=∠2AC=CA∠3=∠4△CDAASACDBC∠D=已知:如图,四边形ABCD是平行四边形。求证:(1)AB=DC,AD=BC
(2) ∠A=∠C ,∠B=∠D∴AB= ,AD= ,
∠ B= .
∵∠1=∠2,∠3=∠4
∴ ∠1+∠4_____∠2+∠3,
即∠BAD= ∠BCD平行四边形的性质:猜想证明 探究性质 如果不添加辅助线,你能证明平行四边形对角相等?1.平行四边形的对边平行且相等
2.平行四边形的对角相等3.平行四边形的邻角互补.平行四边形的性质:ABCD猜想证明 探究性质 请同学们用几何语言描述这三点性质38°应用知识 解决问题 练习1:如图,在 ABCD中,∠B=38°,
则∠A =____,
∠C =____,
∠D =____.142°142°小结:平行四边形中已知一个内角的度数可求出其他三个内角的度数。ABCD应用知识 解决问题 练习2 如图,在 ABCD中,AB=5cm,BC=3cm,
则AD=_____,
CD=_____,
ABCD的周长=_____. 3cm5cm16cm小结:平行四边形两邻边的和等于周长的一半。应用知识 解决问题 练习3 如图,在 ABCD中,AD=8cm,其周长为24cm,求其余三条边的长度.解:∵四边形ABCD是平行四边形
∴AB=CD,BC=AD(平行四边形的对边相等) 又∵AD=8cm
∴BC=AD= 8cm∵AB+BC+CD+AD=24cm
∴AB=CD= (24-8-8) ÷2=4cm即其余三条边的长度分别为
8cm,4cm,4cm.应用知识 解决问题 证明:∵在□ABCD中
∴∠A=∠C,AD=BC ∴△AED ≌△CFB(AAS)
∴AE=CF又∵DE⊥AB,BF⊥CD
∴∠AED=∠CFB=90° 1、平行四边形的定义:2、平行四边形的性质1:有两组对边分别平行的四边形平行四边形的对边相等,对角相等感悟与收获 除了以上两点,本节课你还有其他收获吗?1、复习本节课内容2、完成习题18.1第1,2题课后作业 3、预习平行四边形性质2
∴AB∥CD,AD∥BCABCD
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形读作:平行四边形ABCD4.平行四边形中相对的边称为对边,相对的角称为对角。1.定义:ABDC观察生活 形成概念 反之, 细心观察,猜想平行四边形的边、角之间有怎样的
数量关系?说出你的猜想并和同伴交流? 猜想证明 探究性质 实验报告平行四边形的对边相等
平行四边形的对角相等
相等相等互补 猜 想量一量、折一折、看一看证明:连接AC
四边形问题三角形问题转 化猜想证明 探究性质 ∵四边形ABCD为平行四边形,
∴AD∥BC,AB∥CD,
∴∠ 1 = , ∠3 = .
在△ABC和△CDA中
_____________
_____________(公共边)
_____________
∴△ABC ≌ ( ).∠2∠4∠1=∠2AC=CA∠3=∠4△CDAASACDBC∠D=已知:如图,四边形ABCD是平行四边形。求证:(1)AB=DC,AD=BC
(2) ∠A=∠C ,∠B=∠D∴AB= ,AD= ,
∠ B= .
∵∠1=∠2,∠3=∠4
∴ ∠1+∠4_____∠2+∠3,
即∠BAD= ∠BCD平行四边形的性质:猜想证明 探究性质 如果不添加辅助线,你能证明平行四边形对角相等?1.平行四边形的对边平行且相等
2.平行四边形的对角相等3.平行四边形的邻角互补.平行四边形的性质:ABCD猜想证明 探究性质 请同学们用几何语言描述这三点性质38°应用知识 解决问题 练习1:如图,在 ABCD中,∠B=38°,
则∠A =____,
∠C =____,
∠D =____.142°142°小结:平行四边形中已知一个内角的度数可求出其他三个内角的度数。ABCD应用知识 解决问题 练习2 如图,在 ABCD中,AB=5cm,BC=3cm,
则AD=_____,
CD=_____,
ABCD的周长=_____. 3cm5cm16cm小结:平行四边形两邻边的和等于周长的一半。应用知识 解决问题 练习3 如图,在 ABCD中,AD=8cm,其周长为24cm,求其余三条边的长度.解:∵四边形ABCD是平行四边形
∴AB=CD,BC=AD(平行四边形的对边相等) 又∵AD=8cm
∴BC=AD= 8cm∵AB+BC+CD+AD=24cm
∴AB=CD= (24-8-8) ÷2=4cm即其余三条边的长度分别为
8cm,4cm,4cm.应用知识 解决问题 证明:∵在□ABCD中
∴∠A=∠C,AD=BC ∴△AED ≌△CFB(AAS)
∴AE=CF又∵DE⊥AB,BF⊥CD
∴∠AED=∠CFB=90° 1、平行四边形的定义:2、平行四边形的性质1:有两组对边分别平行的四边形平行四边形的对边相等,对角相等感悟与收获 除了以上两点,本节课你还有其他收获吗?1、复习本节课内容2、完成习题18.1第1,2题课后作业 3、预习平行四边形性质2
