10.2 阿基米德原理 提高提升测试卷
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
浮力提高练习题
一、选择题(共11题)
1.底面积为400cm2的圆柱形水槽内盛有适量的水。现将质量为1kg、横截面积为100cm2的圆柱形物体A,用细线悬挂后让其浸入水中,当物体A露出其总体积的时,细线对物体A的拉力为F1,如图甲所示;向圆柱形水槽内加水,水始终未溢出,当物体A完全浸没在水中时,细线对物体A的拉力为F2,如图乙所示。已知:F1:F2=2:1,g取10N/kg,则下列判断正确的是( )
A.物体A的密度为1.6×103kg/m3 B.物体A的体积为750cm3
C.物体A的所受拉力F1为3.75N D.向圆柱形水槽内加水的质量为625g
2.如图所示,长方体金属块在细绳竖直向上拉力作用下从水中开始一直竖直向上做匀速直线运动,上升到离水面一定的高度处。图乙是绳子拉力F随时间t变化的图象,取g=10N/Kg.根据图象信息,下列判断正确的是( )
A.该金属块重力的大小为34N
B.该金属块的密度是2.7×103kg/m3
C.浸在水中的金属块受到的浮力大小是34N
D.在t1至t2时间段金属块在水中受到的浮力逐渐增大
3.修建大桥在水下施工时,要向江中沉放大量的施工构件,假设一边长3m的正方体构件被缓缓吊入水中(如图甲所示)在沉入过程中,其下表面到水面的距离为h,随着h的增大,钢绳拉力F、物体所受浮力F浮的变化如图乙所示。则以下说法正确的是( )
A.该正方体的质量是2.7×104Kg B.该正方体的密度是2×103Kg/m3
C.图线①反映了浮力随时间变化情况 D.由图可知浮力随深度增加而增大
4.在A、B、C三个相同的容器盛有质量相同的不同液体,如图。将三个相同的铁球分别沉入容器底部,静止时,铁球对容器底的压力( )
A.A的最小 B.B的最小 C.C的最小 D.一样大
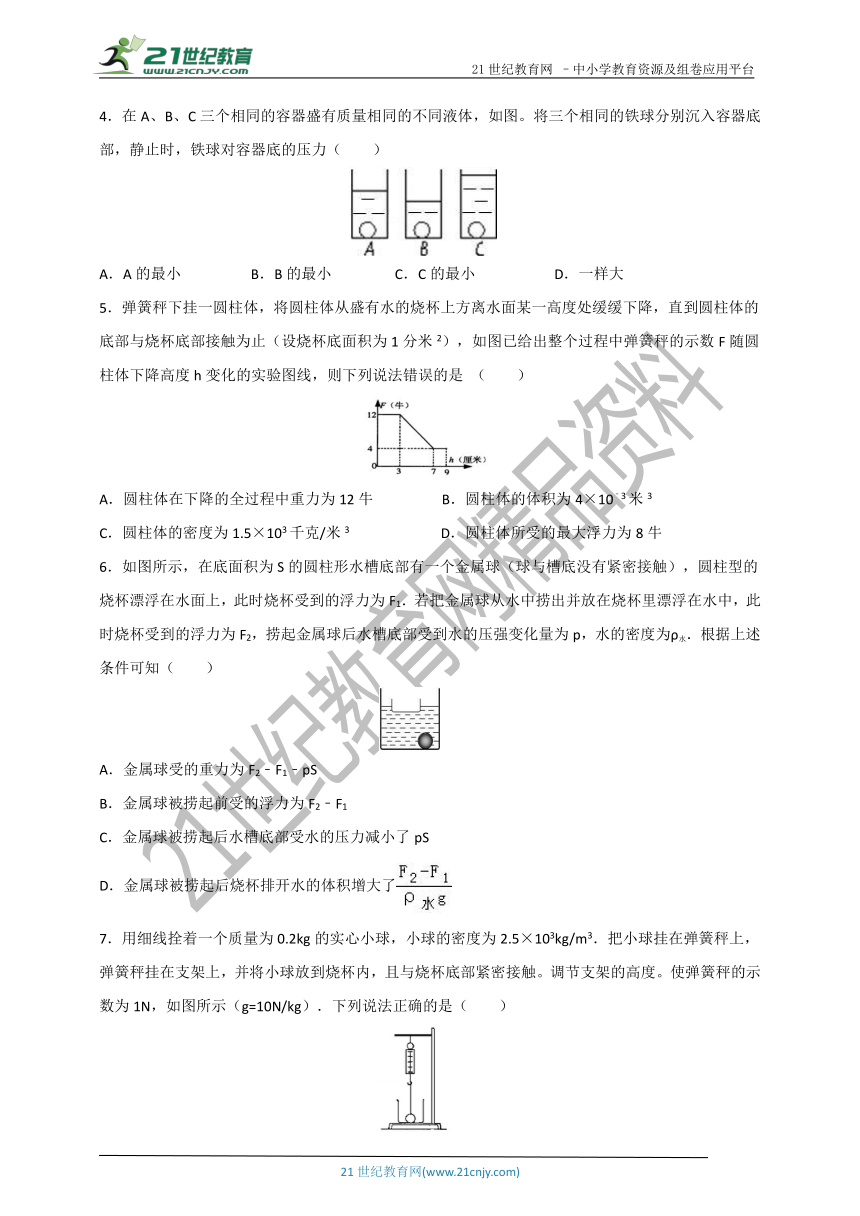
5.弹簧秤下挂一圆柱体,将圆柱体从盛有水的烧杯上方离水面某一高度处缓缓下降,直到圆柱体的底部与烧杯底部接触为止(设烧杯底面积为1分米2),如图已给出整个过程中弹簧秤的示数F随圆柱体下降高度h变化的实验图线,则下列说法错误的是 ( )
A.圆柱体在下降的全过程中重力为12牛 B.圆柱体的体积为4×10﹣3米3
C.圆柱体的密度为1.5×103千克/米3 D.圆柱体所受的最大浮力为8牛
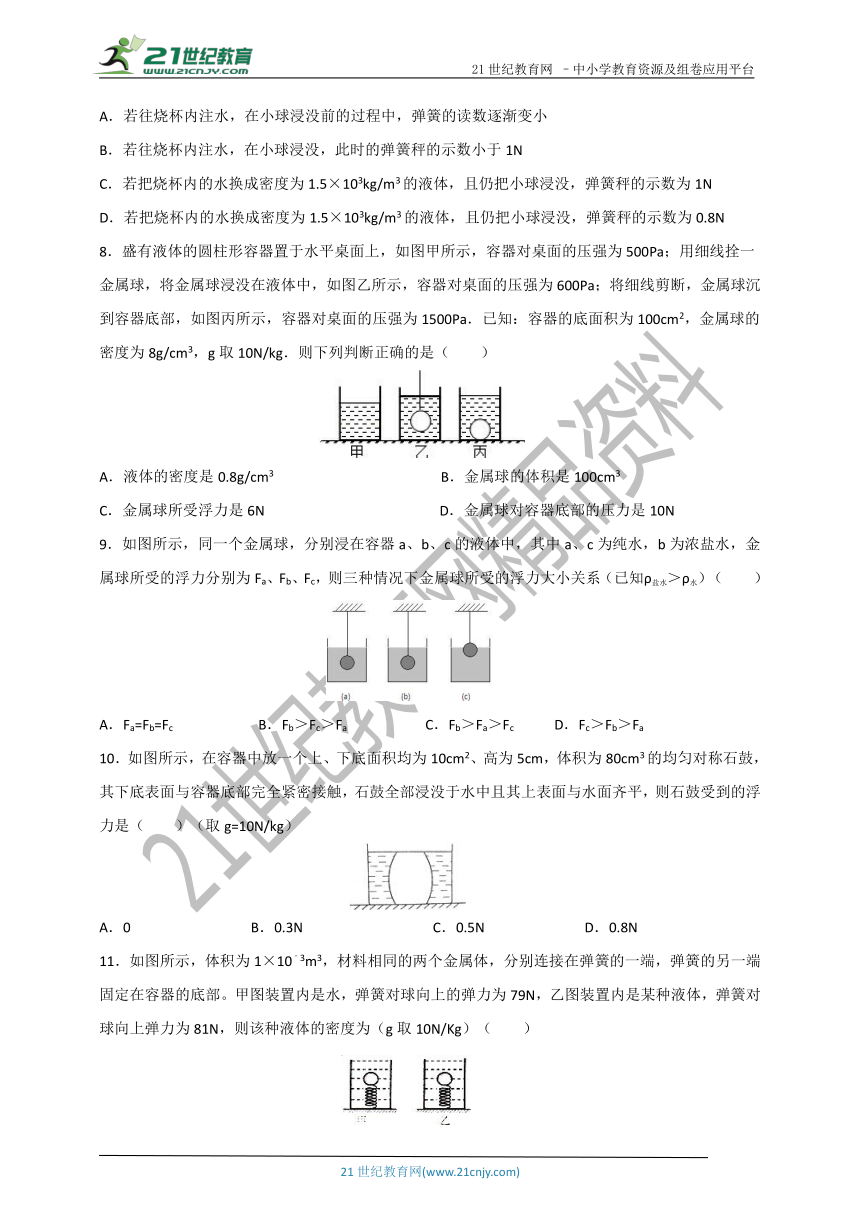
6.如图所示,在底面积为S的圆柱形水槽底部有一个金属球(球与槽底没有紧密接触),圆柱型的烧杯漂浮在水面上,此时烧杯受到的浮力为F1.若把金属球从水中捞出并放在烧杯里漂浮在水中,此时烧杯受到的浮力为F2,捞起金属球后水槽底部受到水的压强变化量为p,水的密度为ρ水.根据上述条件可知( )
A.金属球受的重力为F2﹣F1﹣pS
B.金属球被捞起前受的浮力为F2﹣F1
C.金属球被捞起后水槽底部受水的压力减小了pS
D.金属球被捞起后烧杯排开水的体积增大了
7.用细线拴着一个质量为0.2kg的实心小球,小球的密度为2.5×103kg/m3.把小球挂在弹簧秤上,弹簧秤挂在支架上,并将小球放到烧杯内,且与烧杯底部紧密接触。调节支架的高度。使弹簧秤的示数为1N,如图所示(g=10N/kg).下列说法正确的是( )
A.若往烧杯内注水,在小球浸没前的过程中,弹簧的读数逐渐变小
B.若往烧杯内注水,在小球浸没,此时的弹簧秤的示数小于1N
C.若把烧杯内的水换成密度为1.5×103kg/m3的液体,且仍把小球浸没,弹簧秤的示数为1N
D.若把烧杯内的水换成密度为1.5×103kg/m3的液体,且仍把小球浸没,弹簧秤的示数为0.8N
8.盛有液体的圆柱形容器置于水平桌面上,如图甲所示,容器对桌面的压强为500Pa;用细线拴一金属球,将金属球浸没在液体中,如图乙所示,容器对桌面的压强为600Pa;将细线剪断,金属球沉到容器底部,如图丙所示,容器对桌面的压强为1500Pa.已知:容器的底面积为100cm2,金属球的密度为8g/cm3,g取10N/kg.则下列判断正确的是( )
A.液体的密度是0.8g/cm3 B.金属球的体积是100cm3
C.金属球所受浮力是6N D.金属球对容器底部的压力是10N
9.如图所示,同一个金属球,分别浸在容器a、b、c的液体中,其中a、c为纯水,b为浓盐水,金属球所受的浮力分别为Fa、Fb、Fc,则三种情况下金属球所受的浮力大小关系(已知ρ盐水>ρ水)( )
A.Fa=Fb=Fc B.Fb>Fc>Fa C.Fb>Fa>Fc D.Fc>Fb>Fa
10.如图所示,在容器中放一个上、下底面积均为10cm2、高为5cm,体积为80cm3的均匀对称石鼓,其下底表面与容器底部完全紧密接触,石鼓全部浸没于水中且其上表面与水面齐平,则石鼓受到的浮力是( )(取g=10N/kg)
A.0 B.0.3N C.0.5N D.0.8N
11.如图所示,体积为1×10﹣3m3,材料相同的两个金属体,分别连接在弹簧的一端,弹簧的另一端固定在容器的底部。甲图装置内是水,弹簧对球向上的弹力为79N,乙图装置内是某种液体,弹簧对球向上弹力为81N,则该种液体的密度为(g取10N/Kg)( )
A.7.9×103Kg/m3 B.8.1×103Kg/m3 C.0.8×103Kg/m3 D.0.2×103Kg/m3
二.填空题(共1小题)
12.学习了浮力有关知识后,同学们都已经知道:浮力跟物体所浸在的液体密度、排开液体的体积有关。但王丽总感到:浮力大小应与物体所在液体的深度有关,并猜想:“深度越深,浮力越大”。于是做了如下实验:她在弹簧测力计下挂一圆柱体,从盛水的烧杯上方某一高度缓慢下降,圆柱体浸没后继续下降,直到圆柱体底面接近烧杯底部接触为止,如图所示是圆柱体下降过程中弹簧测力计读数F随圆柱体下降高度h变化的图象。
(1)分析图象可知,圆柱体的重力是 N;
(2)圆柱体浸没在水中时,受到的浮力是 N;
(3)圆柱体的体积是 m3;
(4)圆柱体的密度是 kg/m3;
(5)分析图象BC段,可得结论:物体浸没液体之前,浸入液体的深度越深,受到的浮力越 (选填“大”或“小”);
(6)分析图象CD段,可得结论: 。
三.解析答题(共3小题)
13.如图所示,一个半径为r的实心球体处于某种液体中,球体最上端距离液面的距离为h0,已知液体的密度为ρ,球体的体积为πr3.若将此球沿图中虚线切成两个半球,求:
(1)上半球的横切面受到液体向上的压力;
(2)上半球所受的浮力;
(3)液体对球体向下的压力。
14.小薇在一已调零、能够准确测量的弹簧测力计下悬挂一重为G1、密度为ρ1的金属块,并在测力计刻度盘上力的刻线处分别标注相应的密度值(图中未画出),制成一个可以直接测量液体密度的“密度计”,使用时只需将悬挂的金属块完全浸入待测液体中(如图所示),就可以从刻度盘中“看”出此液体的密度。请你解析答下列问题:
(1)在图中画出正常使用时,金属块沿竖直方向受力的示意图;
(2)推导出被测液体的密度ρ液与弹簧测力计示数F之间的关系式;
(3)若原测力计的分度值为F0,则改装后这只“密度计”的分度值是多少?
15.水平桌面上放置底面积为0.01m2,重为6N的圆筒,筒内装有0.2m深的某液体。弹簧测力计悬挂体积为4×10﹣4m3的圆柱体,从液面逐渐浸入直到浸没,弹簧测力计示数F与圆柱体浸入液体深度h的关系如图所示。(圆筒的厚度忽略不计,筒内液体没有溢出),求:
(1)圆柱体浸没在液体中时所受的浮力是多少?
(2)筒内液体密度是多少?
(3)当圆柱体的一半浸入液体中时,圆筒容器对桌面的压强是多少?
浮力提高练习题
参考答案与解析
一.选择题(共11小题)
1.A。解析:∵F1:F2=2:1,∴(G﹣ρ水g×v):(G﹣ρ水g×v)=2:1;(1kg×10N/kg﹣1×103kg/m3×10N/kg×v):(1kg×10N/kg﹣1×103kg/m3×10N/kg×v)=2:1;v=0.625×10﹣3m3=625cm3;故B错误;物体A的密度:ρA===1.6g/cm3=1.6×103kg/m3;故A正确;F1=G﹣ρ水g×v=1kg×10N/kg﹣1×103kg/m3×10N/kg××0.625×10﹣3m3=7.5N;故C错误;A的高度:h==,加入水的体积v水=(400cm2﹣100cm2)××6.25cm=1125cm3,向圆柱形水槽内加水的质量:m水=ρ水v水=1g/cm3×1125cm3=1125g;故D错误。故选:A。
2.B解析:(1)当金属块完全露出液面,没有浸入水中时,金属块不受浮力,此时拉力等于重力,即为图中的CD段,从图可知,该金属块重力为:G=F拉=54N,故A错。(2)当金属块未露出液面时,即为图中的AB段,从图可知,此时绳子的拉力为34N,则金属块受到的浮力大小为:F浮=G﹣F拉=54N﹣34N=20N.故C错。∵F浮=ρ水v排g,∴金属块排开水的体积(金属块的体积):V金=V排===0.002m3,∵G=mg,∴金属块的质量为:m===5.4kg,
金属块的密度为:ρ金===2.7×103kg/m3.故B正确。(3)从图可知,绳子的拉力在t1至t2时间段内逐渐的变大,则由公式F浮=G﹣F拉可知,金属块的重力不变,而拉力逐渐的变大,所以浮力逐渐变小。故D错。故选:B。
3.B解析:(1)由图象可知,构件在浸入水中的过程时排开水的体积变大,所以浮力逐渐变大;当构件浸没后排开水的体积不变,所以浮力不变,即浮力随深度增加先增大后不变,因此F浮随h变化的图线是图乙中的②,故D错误;(2)钢丝绳的拉力F拉=G﹣F浮,所以据上分析即可判断①反映的是钢绳拉力F随h变化的关系,故C错误;A、构件的体积是V=(3m)3=27m3,当其完全浸没时浮力最大,故其最大浮力:F浮=ρ水gv排=1×103kg/m3×10N/kg×27m3=2.7×105N;由图象构件完全浸没时的拉力与浮力相等,故此时的拉力也是2.7×105N,因为F拉=G﹣F浮,所以G=F浮+F拉=5.4×105 N,故A错误;(3)由密度公式,构件密度ρ====2×103kg/m3,故B正确。
4.B解析:(1)由图可知:vC>vA>vB,∵mC=mA=mB,,∴三中液体的密度:ρC<ρA<ρB;
(2)∵三个铁球的体积相同,∴全浸入时,排开液体的体积相同,∴三个铁球受到的浮力:FC<FA<FB;(3)∵铁球沉入容器底部静止时,G=F浮+F支,∴F支=G﹣F浮,∴三个铁球受到的支持力:F支C>F支A>F支B,即B容器中的铁球受到的支持力最小;(4)∵力的作用是相互的,∴B容器中的铁球对容器底的压力最小。故选B:。
5.B.解析:(1)由图象可知,当h=0时,弹簧测力计示数为12N,此时圆柱体在空气中,根据二力平衡条件可知,圆柱体在下降的全过程中重力G=F示=12N.故A正确;(2)对圆柱体受力分析,并结合图象可知,圆柱体所受的最大浮力F浮=G﹣F示=12N﹣4N=8N;由阿基米德原理F浮=ρ液V排g得:
V排===8×10﹣4m3,因为物体是全部浸没,所以V物=V排=8×10﹣4m3,由公式G=mg可求出物体的质量:m===1.2kg,ρ物===1.5×103kg/m3,
故CD正确;B错误;故选:B。
6.D.解析:A、由物体的浮沉条件可知:烧杯的浮力:F1=G烧杯 ,金属球放在烧杯内时受到的浮力:F2=G球+G烧杯,所以,G球=F2﹣F1 ,故A不正确;B、金属球被捞起前沉入水底,所以受到的浮力小于重力,即小于F2﹣F1,故B不正确;C、金属球被捞起后放在烧杯里时,新排开水的体积为=,
因ρ球>ρ水,所以新排开水的体积大于金属球浸没时排开水的体积为,由P=ρgh可知:金属球被捞起后水槽底部受水的压力增大了而不是减小,故C不正确;D、金属球被捞起前烧杯排开水的体积为=;金属球被捞起后烧杯排开水的体积为=;所以金属球被捞起后烧杯排开水的体积增大了,故D正确。
7.D.解析:(1)将小球放到烧杯内且与紧密接触时,G=mg=0.2kg×10N/Kg=2N,则烧杯对小球的支持力为N=G﹣F=2N﹣1N=1N,当往烧杯内注水且把小球浸没时,V排=V球===8×10﹣5m3;小球受到的浮力:F浮=ρ水gV排=1.0×103Kg/m3×10N/Kg×8×10﹣5m3=0.8N;而这时因小球受到的浮力小于烧杯产生的支持力,所以烧杯还必须产生1N﹣0.8N=0.2N的支持力才能使小球静止,弹簧秤对小球的拉力不变,即示数F1为1N不变,故AB错误。(2)若把小球浸没在另一种液体里时,根据阿基米德原理可得:小球受到的浮力F浮2=ρ液gV排=1.5×103Kg/m3×10N/kg×8×10﹣5m3=1.2N>1N;
即小球受到的浮力大于烧杯产生的支持力,所以烧杯不再产生支持力,则小球受到的浮力、拉力和重力的作用,根据物体受力平衡可得:测力计示数为:F2=G﹣F浮2=2N﹣1.2N=0.8N;故C错误,D正确。
故选:D。
8.A.解析:(1)由甲图和丙图可得:△p1=1500Pa﹣500Pa=1000Pa,由于p=,则对桌面增加的压力:△F1=△p1S=1000Pa×100×10﹣4m2=10N,对桌面增加的压力:△F1=G,金属球重:G=10N,金属球的质量:m===1kg=1000g,金属球的体积:V===125cm3,故B错;(2)由甲图和乙图可得,△p2=600Pa﹣500Pa=100Pa,因为p=,则对桌面增加的压力:△F2=△p2S=100Pa×100×10﹣4m2=1N,对桌面增加的压力:△F2=G排,则金属球排开液体的重力:G排=1N,金属球的受到的浮力:F浮=G排=1N,故C错;排开液体的体积:V排=V=125cm3,F浮=ρ液V排g,ρ液===800kg/m3=0.8g/cm3,故A正确;(3)金属球对容器底部的压力:
F=G﹣F浮=10N﹣1N=9N,故D错。故选:A。
9.C.解析:①金属球在a、b液体中所受浮力大小,∵ρ盐水>ρ水,V排a=V排b=V,∴由F浮=ρ液g V排 可得F浮a<F浮b;②金属球在ac中的浮力大小;,∵V排a>V排c,都是在纯水中,即液体密度相等,∴由F浮=ρ液g V排 可得F浮c<F浮a。∴F浮b;>F浮a>F浮c。故选:C。
10.B.解析:石鼓排开水的体积:v排=80cm3﹣10cm2×5cm=30cm3=30×10﹣6m3,石鼓受到水的浮力:
F浮=ρgV排=1.0×103kg/m3×10N/kg×30×10﹣6m3=0.3N。故选:B。
11.C.解析:小球受到重力、弹力以及浮力作用,而弹力大小等于重力与浮力的差;在水中时,小球的重力G=F浮水+F弹水=ρ水gV排+F弹水=1000kg/m3×10N/kg×1×10﹣3m3+79N=89N,在某种液体中,小球所受的浮力F浮液=G﹣F弹液=89N﹣81N=8N,所以液体的密度ρ===0.8×103kg/m3。故选:C。
二.填空题(共1小题)
12.(1)12;(2)8;(3)8×10﹣4;(4)1.5×103;(5)大;(6)物体浸没到液体中后,浮力大小不变或者说物体浸没到液体中后,物体所受的浮力与物体浸入的深度无关。
解析:(1)由图象可知,当h=0时,弹簧测力计示数为12N,此时圆柱体处于空气中,根据二力平衡条件可知,G=F拉=12N。
(2)从h=7cm开始,弹簧测力计示数不变,说明此时圆柱体已经浸没在水中,对圆柱体受力分析可知,F浮=G﹣F拉=12N﹣4N=8N。
(3)由阿基米德原理F浮=ρ液V排g得:V排===8×10﹣4m3,
∵物体是全部浸没,∴V物=V排=8×10﹣4m3,
(4)由公式G=mg可求出物体的质量,m===1.2kg,ρ物===1.5×103kg/m3;
(5)分析图象BC段,物体在液体中的深度逐渐增加,测力计读数在减小,说明物体在慢慢浸入水中,V排在逐渐增大,物体受到的浮力也在逐渐增大。
(6)分析图象CD段,深度在增加,而测力计的读数不变,说明物体全部浸没水中,V排不变,浮力不变。
三.选择题(共3小题)
13.(1)上半球的横切面受到液体向上的压力为ρg(h0+r)πr2;
(2)上半球所受的浮力为ρgπr3;
(3)液体对球体向下的压力为ρgπr2(h0+)。
解析:(1)将球体分成上、下相等的两个半球,上半球下底面大深度为h=h0+r,
则上半球的横切面受到液体向上的压强:p=ρgh=ρg(h0+r),由p=可得,上半球下表面受到的压力:
F下=pS=ρg(h0+r)πr2;
(2)上半球受到的浮力:F浮=ρgV排1=ρg×V球=ρg××πr3=ρgπr3;
(3)由F浮=F下﹣F上可得,液体对球体向下的压力:F上=F下﹣F浮=ρg(h0+r)πr2﹣ρgπr3=ρgh0πr2+ρgπr3=ρgπr2(h0+)。
14.(1)受力示意图如上;
(2)被测液体的密度ρ液与弹簧测力计示数F之间的关系式是ρ液=ρ1﹣F;
(3)改装后这只“密度计”的分度值是F0。
解析:(1)金属块处于静止,受F、F浮、G的作用 ,受力的示意图如下:
(2)由于金属块处于静止,则F+F浮=G1,由F浮=ρ液gV排得:F+ρ液gV=G1,ρ液===ρ1﹣F;
(3)当拉力在F1时,液体的密度为ρ液1=ρ1﹣F1,若原测力计的分度值为F0,当拉力在F2=F1﹣F0,则液体的密度为ρ液2=ρ1﹣F2=ρ1﹣(F1﹣F0),所以密度计的分度值ρ0=ρ液2﹣ρ液1=ρ1﹣(F1﹣F0)﹣(ρ1﹣F1)=F0。
15.(1)圆柱体浸没在液体中所受浮力是8N;
(2)筒内液体的密度是2×103kg/m3;
(3)当圆柱体的一半浸入液体中时,圆筒对桌面的压强是5×103Pa。
解析:(1)由图象知,当h=0时,此时测力计的示数等于圆柱体的重力,所以G=10N;当h≥8cm时,测力计的示数不变,说明此时浮力不变,圆柱体完全浸没,此时F=2N;所以F浮=G﹣F=10N﹣2N=8N;
(2)物体排开液体的体积V排=V物=4×10﹣4m3,由F浮=ρ液gV排得,ρ液===2×103kg/m3;
(3)液体的质量m液=ρ液V液=2×103kg/m3×0.01m2×0.2m=4kg,当圆柱体的一半浸入液体中时,F浮′=F浮=×8=4N;∴F拉=G﹣F浮′=10N﹣4N=6N;将圆柱体、圆筒、液体看做一个整体,则其对地面的压力:
F′=m液g+G筒+G物﹣F拉=4kg×10N/kg+6N+10N﹣6N=50N,p===5×103Pa。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浮力提高练习题
一、选择题(共11题)
1.底面积为400cm2的圆柱形水槽内盛有适量的水。现将质量为1kg、横截面积为100cm2的圆柱形物体A,用细线悬挂后让其浸入水中,当物体A露出其总体积的时,细线对物体A的拉力为F1,如图甲所示;向圆柱形水槽内加水,水始终未溢出,当物体A完全浸没在水中时,细线对物体A的拉力为F2,如图乙所示。已知:F1:F2=2:1,g取10N/kg,则下列判断正确的是( )
A.物体A的密度为1.6×103kg/m3 B.物体A的体积为750cm3
C.物体A的所受拉力F1为3.75N D.向圆柱形水槽内加水的质量为625g
2.如图所示,长方体金属块在细绳竖直向上拉力作用下从水中开始一直竖直向上做匀速直线运动,上升到离水面一定的高度处。图乙是绳子拉力F随时间t变化的图象,取g=10N/Kg.根据图象信息,下列判断正确的是( )
A.该金属块重力的大小为34N
B.该金属块的密度是2.7×103kg/m3
C.浸在水中的金属块受到的浮力大小是34N
D.在t1至t2时间段金属块在水中受到的浮力逐渐增大
3.修建大桥在水下施工时,要向江中沉放大量的施工构件,假设一边长3m的正方体构件被缓缓吊入水中(如图甲所示)在沉入过程中,其下表面到水面的距离为h,随着h的增大,钢绳拉力F、物体所受浮力F浮的变化如图乙所示。则以下说法正确的是( )
A.该正方体的质量是2.7×104Kg B.该正方体的密度是2×103Kg/m3
C.图线①反映了浮力随时间变化情况 D.由图可知浮力随深度增加而增大
4.在A、B、C三个相同的容器盛有质量相同的不同液体,如图。将三个相同的铁球分别沉入容器底部,静止时,铁球对容器底的压力( )
A.A的最小 B.B的最小 C.C的最小 D.一样大
5.弹簧秤下挂一圆柱体,将圆柱体从盛有水的烧杯上方离水面某一高度处缓缓下降,直到圆柱体的底部与烧杯底部接触为止(设烧杯底面积为1分米2),如图已给出整个过程中弹簧秤的示数F随圆柱体下降高度h变化的实验图线,则下列说法错误的是 ( )
A.圆柱体在下降的全过程中重力为12牛 B.圆柱体的体积为4×10﹣3米3
C.圆柱体的密度为1.5×103千克/米3 D.圆柱体所受的最大浮力为8牛
6.如图所示,在底面积为S的圆柱形水槽底部有一个金属球(球与槽底没有紧密接触),圆柱型的烧杯漂浮在水面上,此时烧杯受到的浮力为F1.若把金属球从水中捞出并放在烧杯里漂浮在水中,此时烧杯受到的浮力为F2,捞起金属球后水槽底部受到水的压强变化量为p,水的密度为ρ水.根据上述条件可知( )
A.金属球受的重力为F2﹣F1﹣pS
B.金属球被捞起前受的浮力为F2﹣F1
C.金属球被捞起后水槽底部受水的压力减小了pS
D.金属球被捞起后烧杯排开水的体积增大了
7.用细线拴着一个质量为0.2kg的实心小球,小球的密度为2.5×103kg/m3.把小球挂在弹簧秤上,弹簧秤挂在支架上,并将小球放到烧杯内,且与烧杯底部紧密接触。调节支架的高度。使弹簧秤的示数为1N,如图所示(g=10N/kg).下列说法正确的是( )
A.若往烧杯内注水,在小球浸没前的过程中,弹簧的读数逐渐变小
B.若往烧杯内注水,在小球浸没,此时的弹簧秤的示数小于1N
C.若把烧杯内的水换成密度为1.5×103kg/m3的液体,且仍把小球浸没,弹簧秤的示数为1N
D.若把烧杯内的水换成密度为1.5×103kg/m3的液体,且仍把小球浸没,弹簧秤的示数为0.8N
8.盛有液体的圆柱形容器置于水平桌面上,如图甲所示,容器对桌面的压强为500Pa;用细线拴一金属球,将金属球浸没在液体中,如图乙所示,容器对桌面的压强为600Pa;将细线剪断,金属球沉到容器底部,如图丙所示,容器对桌面的压强为1500Pa.已知:容器的底面积为100cm2,金属球的密度为8g/cm3,g取10N/kg.则下列判断正确的是( )
A.液体的密度是0.8g/cm3 B.金属球的体积是100cm3
C.金属球所受浮力是6N D.金属球对容器底部的压力是10N
9.如图所示,同一个金属球,分别浸在容器a、b、c的液体中,其中a、c为纯水,b为浓盐水,金属球所受的浮力分别为Fa、Fb、Fc,则三种情况下金属球所受的浮力大小关系(已知ρ盐水>ρ水)( )
A.Fa=Fb=Fc B.Fb>Fc>Fa C.Fb>Fa>Fc D.Fc>Fb>Fa
10.如图所示,在容器中放一个上、下底面积均为10cm2、高为5cm,体积为80cm3的均匀对称石鼓,其下底表面与容器底部完全紧密接触,石鼓全部浸没于水中且其上表面与水面齐平,则石鼓受到的浮力是( )(取g=10N/kg)
A.0 B.0.3N C.0.5N D.0.8N
11.如图所示,体积为1×10﹣3m3,材料相同的两个金属体,分别连接在弹簧的一端,弹簧的另一端固定在容器的底部。甲图装置内是水,弹簧对球向上的弹力为79N,乙图装置内是某种液体,弹簧对球向上弹力为81N,则该种液体的密度为(g取10N/Kg)( )
A.7.9×103Kg/m3 B.8.1×103Kg/m3 C.0.8×103Kg/m3 D.0.2×103Kg/m3
二.填空题(共1小题)
12.学习了浮力有关知识后,同学们都已经知道:浮力跟物体所浸在的液体密度、排开液体的体积有关。但王丽总感到:浮力大小应与物体所在液体的深度有关,并猜想:“深度越深,浮力越大”。于是做了如下实验:她在弹簧测力计下挂一圆柱体,从盛水的烧杯上方某一高度缓慢下降,圆柱体浸没后继续下降,直到圆柱体底面接近烧杯底部接触为止,如图所示是圆柱体下降过程中弹簧测力计读数F随圆柱体下降高度h变化的图象。
(1)分析图象可知,圆柱体的重力是 N;
(2)圆柱体浸没在水中时,受到的浮力是 N;
(3)圆柱体的体积是 m3;
(4)圆柱体的密度是 kg/m3;
(5)分析图象BC段,可得结论:物体浸没液体之前,浸入液体的深度越深,受到的浮力越 (选填“大”或“小”);
(6)分析图象CD段,可得结论: 。
三.解析答题(共3小题)
13.如图所示,一个半径为r的实心球体处于某种液体中,球体最上端距离液面的距离为h0,已知液体的密度为ρ,球体的体积为πr3.若将此球沿图中虚线切成两个半球,求:
(1)上半球的横切面受到液体向上的压力;
(2)上半球所受的浮力;
(3)液体对球体向下的压力。
14.小薇在一已调零、能够准确测量的弹簧测力计下悬挂一重为G1、密度为ρ1的金属块,并在测力计刻度盘上力的刻线处分别标注相应的密度值(图中未画出),制成一个可以直接测量液体密度的“密度计”,使用时只需将悬挂的金属块完全浸入待测液体中(如图所示),就可以从刻度盘中“看”出此液体的密度。请你解析答下列问题:
(1)在图中画出正常使用时,金属块沿竖直方向受力的示意图;
(2)推导出被测液体的密度ρ液与弹簧测力计示数F之间的关系式;
(3)若原测力计的分度值为F0,则改装后这只“密度计”的分度值是多少?
15.水平桌面上放置底面积为0.01m2,重为6N的圆筒,筒内装有0.2m深的某液体。弹簧测力计悬挂体积为4×10﹣4m3的圆柱体,从液面逐渐浸入直到浸没,弹簧测力计示数F与圆柱体浸入液体深度h的关系如图所示。(圆筒的厚度忽略不计,筒内液体没有溢出),求:
(1)圆柱体浸没在液体中时所受的浮力是多少?
(2)筒内液体密度是多少?
(3)当圆柱体的一半浸入液体中时,圆筒容器对桌面的压强是多少?
浮力提高练习题
参考答案与解析
一.选择题(共11小题)
1.A。解析:∵F1:F2=2:1,∴(G﹣ρ水g×v):(G﹣ρ水g×v)=2:1;(1kg×10N/kg﹣1×103kg/m3×10N/kg×v):(1kg×10N/kg﹣1×103kg/m3×10N/kg×v)=2:1;v=0.625×10﹣3m3=625cm3;故B错误;物体A的密度:ρA===1.6g/cm3=1.6×103kg/m3;故A正确;F1=G﹣ρ水g×v=1kg×10N/kg﹣1×103kg/m3×10N/kg××0.625×10﹣3m3=7.5N;故C错误;A的高度:h==,加入水的体积v水=(400cm2﹣100cm2)××6.25cm=1125cm3,向圆柱形水槽内加水的质量:m水=ρ水v水=1g/cm3×1125cm3=1125g;故D错误。故选:A。
2.B解析:(1)当金属块完全露出液面,没有浸入水中时,金属块不受浮力,此时拉力等于重力,即为图中的CD段,从图可知,该金属块重力为:G=F拉=54N,故A错。(2)当金属块未露出液面时,即为图中的AB段,从图可知,此时绳子的拉力为34N,则金属块受到的浮力大小为:F浮=G﹣F拉=54N﹣34N=20N.故C错。∵F浮=ρ水v排g,∴金属块排开水的体积(金属块的体积):V金=V排===0.002m3,∵G=mg,∴金属块的质量为:m===5.4kg,
金属块的密度为:ρ金===2.7×103kg/m3.故B正确。(3)从图可知,绳子的拉力在t1至t2时间段内逐渐的变大,则由公式F浮=G﹣F拉可知,金属块的重力不变,而拉力逐渐的变大,所以浮力逐渐变小。故D错。故选:B。
3.B解析:(1)由图象可知,构件在浸入水中的过程时排开水的体积变大,所以浮力逐渐变大;当构件浸没后排开水的体积不变,所以浮力不变,即浮力随深度增加先增大后不变,因此F浮随h变化的图线是图乙中的②,故D错误;(2)钢丝绳的拉力F拉=G﹣F浮,所以据上分析即可判断①反映的是钢绳拉力F随h变化的关系,故C错误;A、构件的体积是V=(3m)3=27m3,当其完全浸没时浮力最大,故其最大浮力:F浮=ρ水gv排=1×103kg/m3×10N/kg×27m3=2.7×105N;由图象构件完全浸没时的拉力与浮力相等,故此时的拉力也是2.7×105N,因为F拉=G﹣F浮,所以G=F浮+F拉=5.4×105 N,故A错误;(3)由密度公式,构件密度ρ====2×103kg/m3,故B正确。
4.B解析:(1)由图可知:vC>vA>vB,∵mC=mA=mB,,∴三中液体的密度:ρC<ρA<ρB;
(2)∵三个铁球的体积相同,∴全浸入时,排开液体的体积相同,∴三个铁球受到的浮力:FC<FA<FB;(3)∵铁球沉入容器底部静止时,G=F浮+F支,∴F支=G﹣F浮,∴三个铁球受到的支持力:F支C>F支A>F支B,即B容器中的铁球受到的支持力最小;(4)∵力的作用是相互的,∴B容器中的铁球对容器底的压力最小。故选B:。
5.B.解析:(1)由图象可知,当h=0时,弹簧测力计示数为12N,此时圆柱体在空气中,根据二力平衡条件可知,圆柱体在下降的全过程中重力G=F示=12N.故A正确;(2)对圆柱体受力分析,并结合图象可知,圆柱体所受的最大浮力F浮=G﹣F示=12N﹣4N=8N;由阿基米德原理F浮=ρ液V排g得:
V排===8×10﹣4m3,因为物体是全部浸没,所以V物=V排=8×10﹣4m3,由公式G=mg可求出物体的质量:m===1.2kg,ρ物===1.5×103kg/m3,
故CD正确;B错误;故选:B。
6.D.解析:A、由物体的浮沉条件可知:烧杯的浮力:F1=G烧杯 ,金属球放在烧杯内时受到的浮力:F2=G球+G烧杯,所以,G球=F2﹣F1 ,故A不正确;B、金属球被捞起前沉入水底,所以受到的浮力小于重力,即小于F2﹣F1,故B不正确;C、金属球被捞起后放在烧杯里时,新排开水的体积为=,
因ρ球>ρ水,所以新排开水的体积大于金属球浸没时排开水的体积为,由P=ρgh可知:金属球被捞起后水槽底部受水的压力增大了而不是减小,故C不正确;D、金属球被捞起前烧杯排开水的体积为=;金属球被捞起后烧杯排开水的体积为=;所以金属球被捞起后烧杯排开水的体积增大了,故D正确。
7.D.解析:(1)将小球放到烧杯内且与紧密接触时,G=mg=0.2kg×10N/Kg=2N,则烧杯对小球的支持力为N=G﹣F=2N﹣1N=1N,当往烧杯内注水且把小球浸没时,V排=V球===8×10﹣5m3;小球受到的浮力:F浮=ρ水gV排=1.0×103Kg/m3×10N/Kg×8×10﹣5m3=0.8N;而这时因小球受到的浮力小于烧杯产生的支持力,所以烧杯还必须产生1N﹣0.8N=0.2N的支持力才能使小球静止,弹簧秤对小球的拉力不变,即示数F1为1N不变,故AB错误。(2)若把小球浸没在另一种液体里时,根据阿基米德原理可得:小球受到的浮力F浮2=ρ液gV排=1.5×103Kg/m3×10N/kg×8×10﹣5m3=1.2N>1N;
即小球受到的浮力大于烧杯产生的支持力,所以烧杯不再产生支持力,则小球受到的浮力、拉力和重力的作用,根据物体受力平衡可得:测力计示数为:F2=G﹣F浮2=2N﹣1.2N=0.8N;故C错误,D正确。
故选:D。
8.A.解析:(1)由甲图和丙图可得:△p1=1500Pa﹣500Pa=1000Pa,由于p=,则对桌面增加的压力:△F1=△p1S=1000Pa×100×10﹣4m2=10N,对桌面增加的压力:△F1=G,金属球重:G=10N,金属球的质量:m===1kg=1000g,金属球的体积:V===125cm3,故B错;(2)由甲图和乙图可得,△p2=600Pa﹣500Pa=100Pa,因为p=,则对桌面增加的压力:△F2=△p2S=100Pa×100×10﹣4m2=1N,对桌面增加的压力:△F2=G排,则金属球排开液体的重力:G排=1N,金属球的受到的浮力:F浮=G排=1N,故C错;排开液体的体积:V排=V=125cm3,F浮=ρ液V排g,ρ液===800kg/m3=0.8g/cm3,故A正确;(3)金属球对容器底部的压力:
F=G﹣F浮=10N﹣1N=9N,故D错。故选:A。
9.C.解析:①金属球在a、b液体中所受浮力大小,∵ρ盐水>ρ水,V排a=V排b=V,∴由F浮=ρ液g V排 可得F浮a<F浮b;②金属球在ac中的浮力大小;,∵V排a>V排c,都是在纯水中,即液体密度相等,∴由F浮=ρ液g V排 可得F浮c<F浮a。∴F浮b;>F浮a>F浮c。故选:C。
10.B.解析:石鼓排开水的体积:v排=80cm3﹣10cm2×5cm=30cm3=30×10﹣6m3,石鼓受到水的浮力:
F浮=ρgV排=1.0×103kg/m3×10N/kg×30×10﹣6m3=0.3N。故选:B。
11.C.解析:小球受到重力、弹力以及浮力作用,而弹力大小等于重力与浮力的差;在水中时,小球的重力G=F浮水+F弹水=ρ水gV排+F弹水=1000kg/m3×10N/kg×1×10﹣3m3+79N=89N,在某种液体中,小球所受的浮力F浮液=G﹣F弹液=89N﹣81N=8N,所以液体的密度ρ===0.8×103kg/m3。故选:C。
二.填空题(共1小题)
12.(1)12;(2)8;(3)8×10﹣4;(4)1.5×103;(5)大;(6)物体浸没到液体中后,浮力大小不变或者说物体浸没到液体中后,物体所受的浮力与物体浸入的深度无关。
解析:(1)由图象可知,当h=0时,弹簧测力计示数为12N,此时圆柱体处于空气中,根据二力平衡条件可知,G=F拉=12N。
(2)从h=7cm开始,弹簧测力计示数不变,说明此时圆柱体已经浸没在水中,对圆柱体受力分析可知,F浮=G﹣F拉=12N﹣4N=8N。
(3)由阿基米德原理F浮=ρ液V排g得:V排===8×10﹣4m3,
∵物体是全部浸没,∴V物=V排=8×10﹣4m3,
(4)由公式G=mg可求出物体的质量,m===1.2kg,ρ物===1.5×103kg/m3;
(5)分析图象BC段,物体在液体中的深度逐渐增加,测力计读数在减小,说明物体在慢慢浸入水中,V排在逐渐增大,物体受到的浮力也在逐渐增大。
(6)分析图象CD段,深度在增加,而测力计的读数不变,说明物体全部浸没水中,V排不变,浮力不变。
三.选择题(共3小题)
13.(1)上半球的横切面受到液体向上的压力为ρg(h0+r)πr2;
(2)上半球所受的浮力为ρgπr3;
(3)液体对球体向下的压力为ρgπr2(h0+)。
解析:(1)将球体分成上、下相等的两个半球,上半球下底面大深度为h=h0+r,
则上半球的横切面受到液体向上的压强:p=ρgh=ρg(h0+r),由p=可得,上半球下表面受到的压力:
F下=pS=ρg(h0+r)πr2;
(2)上半球受到的浮力:F浮=ρgV排1=ρg×V球=ρg××πr3=ρgπr3;
(3)由F浮=F下﹣F上可得,液体对球体向下的压力:F上=F下﹣F浮=ρg(h0+r)πr2﹣ρgπr3=ρgh0πr2+ρgπr3=ρgπr2(h0+)。
14.(1)受力示意图如上;
(2)被测液体的密度ρ液与弹簧测力计示数F之间的关系式是ρ液=ρ1﹣F;
(3)改装后这只“密度计”的分度值是F0。
解析:(1)金属块处于静止,受F、F浮、G的作用 ,受力的示意图如下:
(2)由于金属块处于静止,则F+F浮=G1,由F浮=ρ液gV排得:F+ρ液gV=G1,ρ液===ρ1﹣F;
(3)当拉力在F1时,液体的密度为ρ液1=ρ1﹣F1,若原测力计的分度值为F0,当拉力在F2=F1﹣F0,则液体的密度为ρ液2=ρ1﹣F2=ρ1﹣(F1﹣F0),所以密度计的分度值ρ0=ρ液2﹣ρ液1=ρ1﹣(F1﹣F0)﹣(ρ1﹣F1)=F0。
15.(1)圆柱体浸没在液体中所受浮力是8N;
(2)筒内液体的密度是2×103kg/m3;
(3)当圆柱体的一半浸入液体中时,圆筒对桌面的压强是5×103Pa。
解析:(1)由图象知,当h=0时,此时测力计的示数等于圆柱体的重力,所以G=10N;当h≥8cm时,测力计的示数不变,说明此时浮力不变,圆柱体完全浸没,此时F=2N;所以F浮=G﹣F=10N﹣2N=8N;
(2)物体排开液体的体积V排=V物=4×10﹣4m3,由F浮=ρ液gV排得,ρ液===2×103kg/m3;
(3)液体的质量m液=ρ液V液=2×103kg/m3×0.01m2×0.2m=4kg,当圆柱体的一半浸入液体中时,F浮′=F浮=×8=4N;∴F拉=G﹣F浮′=10N﹣4N=6N;将圆柱体、圆筒、液体看做一个整体,则其对地面的压力:
F′=m液g+G筒+G物﹣F拉=4kg×10N/kg+6N+10N﹣6N=50N,p===5×103Pa。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
