11.2.3实数大小比较、估算无理数的大小、实数的运算 同步作业
文档属性
| 名称 | 11.2.3实数大小比较、估算无理数的大小、实数的运算 同步作业 |

|
|
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-16 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
11.2.3实数大小比较、估算无理数的大小、实数的运算
姓名:__________班级:__________考号:__________
一、选择题
1.下列四个数中,最大的数是( )
A. ﹣2 B. ﹣1 C. 0 D.
2.实数在数轴上对应的点的位置如图所示,这四个数中最大的是( )
A. B. C. D.
3.、、5三个数的大小关系是( )
A. B.
C. D.
4.在1,0,-2,- 四个数中,最小的数是( )
A. 1 B. 0 C. -2 D. -
5.与最接近的整数是( )
A. 5 B. 6 C. 7 D. 8
6.估计的值应在( )
A. 1和2之间 B. 2和3之间 C. 3和4之间 D. 4和5之间
7.已知2+的整数部分是a,小数部分是b,则a2+b2=( )
A. 13﹣2 B. 9+2 C. 11+ D. 7+4
8.一个正方形的面积是12,估计它的边长大小在( )
A. 2与3之间 B. 3与4之间 C. 4与5之间 D. 5与6之间
二、填空题
9.的小数部分是 .
10.的倒数为_____;的算术平方根为_____;比较实数的大小:___.
11.计算:-= ______.
12.在实数中,最大的一个数是______.
13.[x)表示大于x的最小整数,如[2.3)=3,[﹣4)=﹣3,则下列判断:①[﹣8)=﹣9;②[x)﹣x有最大值是1;③[x)﹣x有最小值是0;④x<[x)≤x+1,其中正确的是___(填编号).
14.计算:______________.
15.若四个有理数同时满足:,,,则这四个数从小到大的顺序是_______.
三、解答题
16.李大爷有一块长方形菜地,且菜地的长是宽的2倍。
(1)若菜地的面积为98m2,求菜地的长与宽;
(2)若菜地的面积为90m2,这块菜地的宽是多少?(用根号表示)你能告诉李大爷这块菜地的宽在哪两个整数之间吗?
17.计算:
18.在数轴上表示数, , , ,并把这组数从小到大用“”号连接起来.
19.对于任意实数、,定义关于“”的一种运算如下:.例如.
(1)求的值;
(2)若,且,求的值.
20.阅读理解
∵,即2<<3,∴1<-1<2,
∴-1的整数部分为1,小数部分为-2.
解决问题:
已知a是的整数部分,b是的小数部分,求(-a)3+(b+4)2的平方根.
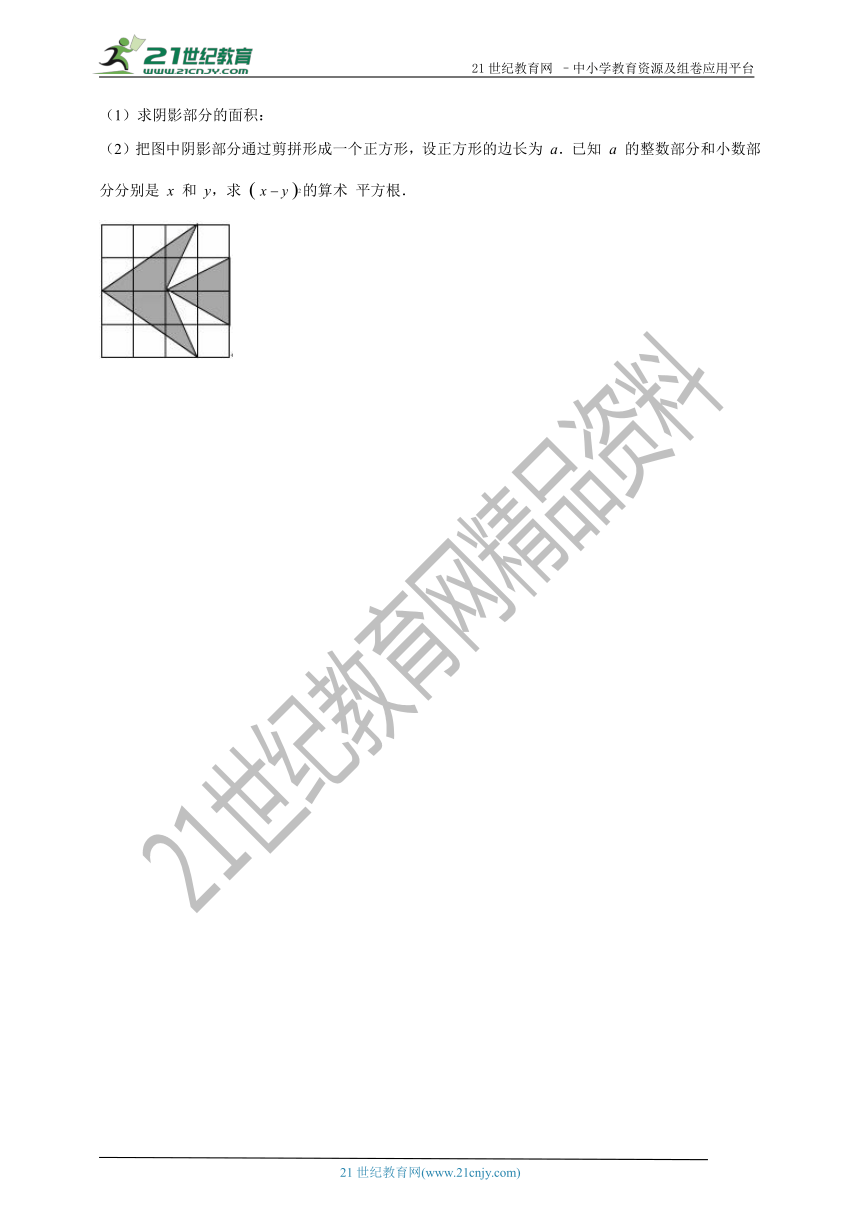
21.如图,网格中每个小正方形的边长为 1,
(1)求阴影部分的面积:
(2)把图中阴影部分通过剪拼形成一个正方形,设正方形的边长为 a.已知 a 的整数部分和小数部分分别是 x 和 y,求 x y 2的算术 平方根.
参考答案
1.D
【解析】分析:正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断即可.
详解:根据实数比较大小的方法,可得
﹣2<﹣1<0<,
所以最大的数是.
故选:D.
点睛:此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
2.D
【解析】分析:根据实数的大小比较解答即可.
详解:由数轴可得:a<b<c<d,
故选D.
点睛:此题考查实数大小比较,关键是根据实数的大小比较解答.
3.A
【解析】分析:根据二次根式的性质把这一组数化为二次根式的形式,再比较被开方数的大小.
详解:这一组数据可化为、、.
∵27>25>24,∴>>,即2<5<.
故选A.
点睛:本题考查的是实数的大小比较,解答此类问题时要根据二次根式的性质把各数化为二次根式的形式,再比较被开方数的大小.
4.C
【解析】分析:实数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.
详解:根据实数比较大小的方法,可得:
1>0>>﹣2,∴在1,0,-2,- 四个数中,最小的一个数是-2.
故选C.
点睛:本题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
5.B
【解析】分析:由题意可知36与37最接近,即与最接近,从而得出答案.
详解:∵36<37<49,
∴<<,即6<<7,
∵37与36最接近,
∴与最接近的是6.
故选:B.
点睛:此题主要考查了无理数的估算能力,关键是整数与最接近,所以=6最接近.
6.B
【解析】【分析】先利用分配律进行计算,然后再进行化简,根据化简的结果即可确定出值的范围.
【详解】
=,
=,
而,
4<<5,
所以2<<3,
所以估计的值应在2和3之间,
故选B.
【点睛】本题主要考查二次根式的混合运算及估算无理数的大小,熟练掌握运算法则以及“夹逼法”是解题的关键.
7.A
【解析】分析:根据无理数的估算,确定出a、b的值,然后代入求解即可.
详解:∵1<<2
∴3<<4
∴a=3,
∴b=-3=-1
∴a2+b2=9+(-1)2=9+3+1-2=13-2.
故选:A.
点睛:此题主要考查了无理数的估算,根据的近似值确定出a、b的值是解题关键.
8.B
【解析】分析:先设正方形的边长等于a,再根据其面积公式求出a的值,估算出a的取值范围即可.
详解:设正方形的边长等于a.
∵正方形的面积是12,∴a==2.
∵9<12<16,∴3<<4,即3<a<4.
故选B.
点睛:本题考查的是估算无理数的大小及算术平方根,估算无理数的大小时要用有理数逼近无理数,求无理数的近似值.
9.﹣4.
【解析】∵42<()2<52,
∴4<<5,
∴的小数部分是﹣4,
故答案为: ﹣4.
点睛:本题考查了无理数的估值,先根据算术平方根的意义估算出的整数部分,再用减去它的整数部分即是它的小数部分.
10. >
【解析】,
∴的倒数为;
∵,
∴的算术平方根为;
∵,
∴.
11.2
【解析】【分析】先分别求算术平方根和立方根,再加减.
【详解】-=5-3=2
故答案为:2
【点睛】本题考核知识点:实数的运算.解题关键点:掌握实数的开方方法.
12.
【解析】分析:根据正数大于0,0大于负数,正数大于负数,比较即可.
详解:根据实数比较大小的方法,可得:
π>>0>>﹣3,故实数其中最大的数是π.
故答案为:π.
点睛:本题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
13.②④
【解析】【分析】根据题意[x)表示大于x的最小整数,结合各项进行判断即可得出答案.
【详解】①[-8)=-8,故①错误;
②[x)-x≤1,即最大值为1,故②正确;
③[x)-x>0,但是取不到0,故③错误;
④因为[x)表示大于x的最小整数,所以存在实数x,x<[x)≤x+1,故④正确,
故答案为:②④.
14.3
【解析】【分析】先分别进行绝对值化简、0次幂的计算,然后再进行加法计算即可得.
【详解】
=2+1
=3,
故答案为:3.
【点睛】本题考查了实数的运算,熟知任何非0数的0次幂为1是解题的关键.
15.
【解析】【分析】根据a>b,a-bd,再结合a+b=c+d,可知c>a,从而可得b>d,由此即可确定最终结果.
【详解】∵a>b,a-b∴c-d>0,即c>d,
又∵a+b=c+d,
∴ad,
∴,
故答案为:.
【点睛】本题考查了实数的大小比较,结合不等式、等式的性质确定出ad是解题的关键.
16.(1)菜地的长为14m,宽为7m;(2)李大爷的菜地的宽在6与7之间
【解析】试题分析:(1)设菜地的宽为xm,则菜地的长为2xm,根据矩形面积公式列方程求解;(2)设菜地的宽为xm,则菜地的长为2xm,求出x的值,然后估算即可.
解:(1)设菜地的宽为xm,则菜地的长为2xm,由题意得,
x×2x=98
∴2x2=98
∴x2=49
∴x=±
∴x=±7
又∵x>0 ∴x=7 ∴2x=14
∴菜地的长为14m,宽为7m。
(2)设菜地的宽为xm,则菜地的长为2xm,由题意得,
x×2x=90
∴2x2=90
∴x2=45
∴x=±
又∵x>0 ∴x=
∴菜地的宽为m。
∵ < <
∴6< <7
∴李大爷的菜地的宽在6与7之间。
点睛:本题考查了矩形的面积公式和平方根的与应用,解答本题的关键是掌握矩形的面积等于长×宽及平方根的意义.
17.1
【解析】分析:先估算无理数的大小,然后根据绝对值的意义即可解答.
详解:原式 1.
点睛:本题考查了估算无理数的大小,绝对值的意义.
18.数轴表示见解析, .
【解析】试题分析:先分别在数轴上找出各数的对应点,然后根据数轴上各点的位置进行大小比较即可.
试题解析:如图
∴这组数的大小关系为.
19.(1);(2).
【解析】分析:(1)根据新定义型运算法则即可求出答案.
(2)列出方程组即可求出答案
详解:(1)
(2)由题意得 ∴.
点睛:本题考查新定义型运算,解题的关键是正确利用运算法则,本题属于基础题型.
20.±4.
【解析】【分析】根据阅读材料的方法先确定出的范围,继而得到a、b的具体数值,然后再代入式子(-a)3+(b+4)2求值,最后再根据平方根的定义进行求解即可.
【详解】∵,即4<<5,∴1<-3<2,
∴-3的整数部分为1,小数部分为-4,
即a=1,b=-4,
∴(-a)3+(b+4)2=-1+17=16,
16的平方根是±4,
即(-a)3+(b+4)2的平方根是±4.
【点睛】本题考查了无理数的估算,阅读题,通过阅读材料找到解决此类问题的方法是关键.
21.(1)6;(2)4
【解析】分析:(1)根据三角形面积公式,求阴影部分的面积=3个三角形面积的和.
(2)由(1)算出a的值,把a的值代入2-a中,表示出x和y,再代入求值即可.
详解:(1)由题意得:S 阴影= ×2×2×2+×2×2=6,
(2)设正方形的边长为a,
由(1)可知:
a2=6,
∵a>0,
∴a=;
∴x 2 , y 2.
x y 2的算术平方根:
,
4 .
点睛:本题考查了算术平方根, 估算无理数的大小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
11.2.3实数大小比较、估算无理数的大小、实数的运算
姓名:__________班级:__________考号:__________
一、选择题
1.下列四个数中,最大的数是( )
A. ﹣2 B. ﹣1 C. 0 D.
2.实数在数轴上对应的点的位置如图所示,这四个数中最大的是( )
A. B. C. D.
3.、、5三个数的大小关系是( )
A. B.
C. D.
4.在1,0,-2,- 四个数中,最小的数是( )
A. 1 B. 0 C. -2 D. -
5.与最接近的整数是( )
A. 5 B. 6 C. 7 D. 8
6.估计的值应在( )
A. 1和2之间 B. 2和3之间 C. 3和4之间 D. 4和5之间
7.已知2+的整数部分是a,小数部分是b,则a2+b2=( )
A. 13﹣2 B. 9+2 C. 11+ D. 7+4
8.一个正方形的面积是12,估计它的边长大小在( )
A. 2与3之间 B. 3与4之间 C. 4与5之间 D. 5与6之间
二、填空题
9.的小数部分是 .
10.的倒数为_____;的算术平方根为_____;比较实数的大小:___.
11.计算:-= ______.
12.在实数中,最大的一个数是______.
13.[x)表示大于x的最小整数,如[2.3)=3,[﹣4)=﹣3,则下列判断:①[﹣8)=﹣9;②[x)﹣x有最大值是1;③[x)﹣x有最小值是0;④x<[x)≤x+1,其中正确的是___(填编号).
14.计算:______________.
15.若四个有理数同时满足:,,,则这四个数从小到大的顺序是_______.
三、解答题
16.李大爷有一块长方形菜地,且菜地的长是宽的2倍。
(1)若菜地的面积为98m2,求菜地的长与宽;
(2)若菜地的面积为90m2,这块菜地的宽是多少?(用根号表示)你能告诉李大爷这块菜地的宽在哪两个整数之间吗?
17.计算:
18.在数轴上表示数, , , ,并把这组数从小到大用“”号连接起来.
19.对于任意实数、,定义关于“”的一种运算如下:.例如.
(1)求的值;
(2)若,且,求的值.
20.阅读理解
∵,即2<<3,∴1<-1<2,
∴-1的整数部分为1,小数部分为-2.
解决问题:
已知a是的整数部分,b是的小数部分,求(-a)3+(b+4)2的平方根.
21.如图,网格中每个小正方形的边长为 1,
(1)求阴影部分的面积:
(2)把图中阴影部分通过剪拼形成一个正方形,设正方形的边长为 a.已知 a 的整数部分和小数部分分别是 x 和 y,求 x y 2的算术 平方根.
参考答案
1.D
【解析】分析:正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断即可.
详解:根据实数比较大小的方法,可得
﹣2<﹣1<0<,
所以最大的数是.
故选:D.
点睛:此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
2.D
【解析】分析:根据实数的大小比较解答即可.
详解:由数轴可得:a<b<c<d,
故选D.
点睛:此题考查实数大小比较,关键是根据实数的大小比较解答.
3.A
【解析】分析:根据二次根式的性质把这一组数化为二次根式的形式,再比较被开方数的大小.
详解:这一组数据可化为、、.
∵27>25>24,∴>>,即2<5<.
故选A.
点睛:本题考查的是实数的大小比较,解答此类问题时要根据二次根式的性质把各数化为二次根式的形式,再比较被开方数的大小.
4.C
【解析】分析:实数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.
详解:根据实数比较大小的方法,可得:
1>0>>﹣2,∴在1,0,-2,- 四个数中,最小的一个数是-2.
故选C.
点睛:本题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
5.B
【解析】分析:由题意可知36与37最接近,即与最接近,从而得出答案.
详解:∵36<37<49,
∴<<,即6<<7,
∵37与36最接近,
∴与最接近的是6.
故选:B.
点睛:此题主要考查了无理数的估算能力,关键是整数与最接近,所以=6最接近.
6.B
【解析】【分析】先利用分配律进行计算,然后再进行化简,根据化简的结果即可确定出值的范围.
【详解】
=,
=,
而,
4<<5,
所以2<<3,
所以估计的值应在2和3之间,
故选B.
【点睛】本题主要考查二次根式的混合运算及估算无理数的大小,熟练掌握运算法则以及“夹逼法”是解题的关键.
7.A
【解析】分析:根据无理数的估算,确定出a、b的值,然后代入求解即可.
详解:∵1<<2
∴3<<4
∴a=3,
∴b=-3=-1
∴a2+b2=9+(-1)2=9+3+1-2=13-2.
故选:A.
点睛:此题主要考查了无理数的估算,根据的近似值确定出a、b的值是解题关键.
8.B
【解析】分析:先设正方形的边长等于a,再根据其面积公式求出a的值,估算出a的取值范围即可.
详解:设正方形的边长等于a.
∵正方形的面积是12,∴a==2.
∵9<12<16,∴3<<4,即3<a<4.
故选B.
点睛:本题考查的是估算无理数的大小及算术平方根,估算无理数的大小时要用有理数逼近无理数,求无理数的近似值.
9.﹣4.
【解析】∵42<()2<52,
∴4<<5,
∴的小数部分是﹣4,
故答案为: ﹣4.
点睛:本题考查了无理数的估值,先根据算术平方根的意义估算出的整数部分,再用减去它的整数部分即是它的小数部分.
10. >
【解析】,
∴的倒数为;
∵,
∴的算术平方根为;
∵,
∴.
11.2
【解析】【分析】先分别求算术平方根和立方根,再加减.
【详解】-=5-3=2
故答案为:2
【点睛】本题考核知识点:实数的运算.解题关键点:掌握实数的开方方法.
12.
【解析】分析:根据正数大于0,0大于负数,正数大于负数,比较即可.
详解:根据实数比较大小的方法,可得:
π>>0>>﹣3,故实数其中最大的数是π.
故答案为:π.
点睛:本题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
13.②④
【解析】【分析】根据题意[x)表示大于x的最小整数,结合各项进行判断即可得出答案.
【详解】①[-8)=-8,故①错误;
②[x)-x≤1,即最大值为1,故②正确;
③[x)-x>0,但是取不到0,故③错误;
④因为[x)表示大于x的最小整数,所以存在实数x,x<[x)≤x+1,故④正确,
故答案为:②④.
14.3
【解析】【分析】先分别进行绝对值化简、0次幂的计算,然后再进行加法计算即可得.
【详解】
=2+1
=3,
故答案为:3.
【点睛】本题考查了实数的运算,熟知任何非0数的0次幂为1是解题的关键.
15.
【解析】【分析】根据a>b,a-b
【详解】∵a>b,a-b
又∵a+b=c+d,
∴a
∴,
故答案为:.
【点睛】本题考查了实数的大小比较,结合不等式、等式的性质确定出a
16.(1)菜地的长为14m,宽为7m;(2)李大爷的菜地的宽在6与7之间
【解析】试题分析:(1)设菜地的宽为xm,则菜地的长为2xm,根据矩形面积公式列方程求解;(2)设菜地的宽为xm,则菜地的长为2xm,求出x的值,然后估算即可.
解:(1)设菜地的宽为xm,则菜地的长为2xm,由题意得,
x×2x=98
∴2x2=98
∴x2=49
∴x=±
∴x=±7
又∵x>0 ∴x=7 ∴2x=14
∴菜地的长为14m,宽为7m。
(2)设菜地的宽为xm,则菜地的长为2xm,由题意得,
x×2x=90
∴2x2=90
∴x2=45
∴x=±
又∵x>0 ∴x=
∴菜地的宽为m。
∵ < <
∴6< <7
∴李大爷的菜地的宽在6与7之间。
点睛:本题考查了矩形的面积公式和平方根的与应用,解答本题的关键是掌握矩形的面积等于长×宽及平方根的意义.
17.1
【解析】分析:先估算无理数的大小,然后根据绝对值的意义即可解答.
详解:原式 1.
点睛:本题考查了估算无理数的大小,绝对值的意义.
18.数轴表示见解析, .
【解析】试题分析:先分别在数轴上找出各数的对应点,然后根据数轴上各点的位置进行大小比较即可.
试题解析:如图
∴这组数的大小关系为.
19.(1);(2).
【解析】分析:(1)根据新定义型运算法则即可求出答案.
(2)列出方程组即可求出答案
详解:(1)
(2)由题意得 ∴.
点睛:本题考查新定义型运算,解题的关键是正确利用运算法则,本题属于基础题型.
20.±4.
【解析】【分析】根据阅读材料的方法先确定出的范围,继而得到a、b的具体数值,然后再代入式子(-a)3+(b+4)2求值,最后再根据平方根的定义进行求解即可.
【详解】∵,即4<<5,∴1<-3<2,
∴-3的整数部分为1,小数部分为-4,
即a=1,b=-4,
∴(-a)3+(b+4)2=-1+17=16,
16的平方根是±4,
即(-a)3+(b+4)2的平方根是±4.
【点睛】本题考查了无理数的估算,阅读题,通过阅读材料找到解决此类问题的方法是关键.
21.(1)6;(2)4
【解析】分析:(1)根据三角形面积公式,求阴影部分的面积=3个三角形面积的和.
(2)由(1)算出a的值,把a的值代入2-a中,表示出x和y,再代入求值即可.
详解:(1)由题意得:S 阴影= ×2×2×2+×2×2=6,
(2)设正方形的边长为a,
由(1)可知:
a2=6,
∵a>0,
∴a=;
∴x 2 , y 2.
x y 2的算术平方根:
,
4 .
点睛:本题考查了算术平方根, 估算无理数的大小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
