11.1.3坐标与图形性质同步作业
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
11.1.3坐标与图形性质同步作业
姓名:__________班级:__________考号:__________
一、选择题
1.平面直角坐标系中,若P(m,n)在第三象限且到x轴,y轴的距离分别为2,3,则点P的坐标为( )
A. (-2,3) B. (-2,-3) C. (3,-2) D. (-3,-2)
2.若点M(3,-2)与点N(x、y)在同一条平行于x轴的直线上,且MN=1,则N点的坐标为( )
A. (4,-2) B. (3,-1) C. (3,-1)或(3,-3) D. (4,-2)或(2,-2)
3.在平面直角坐标系中,点A位于第二象限,距x轴1个单位长度,距y轴4个单位长度,则点A的坐标为( )
A. (1,4) B. (-1,4) C. (-4,1) D. (4,-1)
4.在平面直角坐标系中,一个矩形三个顶点的坐标分别为(-1,-1),(-1,2),(3,-1),则第四个顶点的坐标为( )
A. (2,2) B. (3,2) C. (3,3) D. (2,3)
5.如图,直线m⊥ n,在某平面直角坐标系中,x轴∥ m,y轴∥ n,点A的坐标为(4,2),点B的坐标为(﹣2,﹣2),则点C的坐标为( )
A. (2,1) B. (﹣2,1) C. (2,﹣1) D. (﹣2,﹣1)
6.如图所示为某战役潜伏敌人防御工亭坐标地图的碎片,一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,4),由原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大概( )
A. A处 B. B处 C. C处 D. D处
7.平面直角坐标系内,AB∥ x轴,AB=5,点A的坐标为(1,3),则点B的坐标为( )
A. (-4,3) B. (6,3) C. (-4,3)或(6,3) D. (1,-2)或(1,8)
8.已知A(0,4),点B在x轴上,AB与坐标轴围成的三角形面积为2,则点B的坐标为( )
A. (1,0) B. (1,0)或(-1,0) C. (-1,0) D. (0,-1)或(0,1)
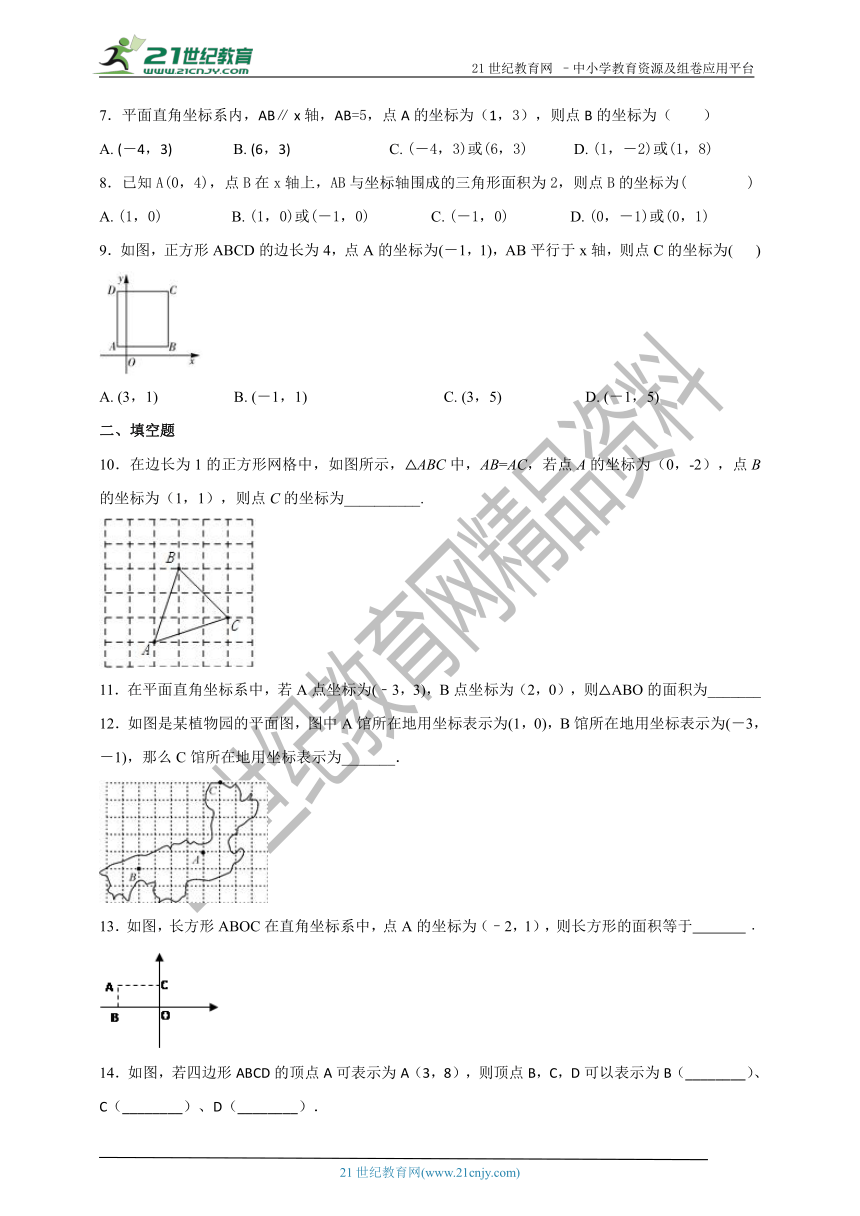
9.如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( )
A. (3,1) B. (-1,1) C. (3,5) D. (-1,5)
二、填空题
10.在边长为1的正方形网格中,如图所示,△ABC中,AB=AC,若点A的坐标为(0,-2),点B的坐标为(1,1),则点C的坐标为__________.
11.在平面直角坐标系中,若A点坐标为(﹣3,3),B点坐标为(2,0),则△ABO的面积为_______
12.如图是某植物园的平面图,图中A馆所在地用坐标表示为(1,0),B馆所在地用坐标表示为(-3,-1),那么C馆所在地用坐标表示为_______.
13.如图,长方形ABOC在直角坐标系中,点A的坐标为(–2,1),则长方形的面积等于 ﹒
14.如图,若四边形ABCD的顶点A可表示为A(3,8),则顶点B,C,D可以表示为B(________)、C(________)、D(________).
15.已知点A(-3,2),点B(1,4),
(1)若CA平行于x轴,BC平行于y轴,则点C的坐标是______ ;
(2)若CA平行于y轴,BC平行于x轴,则点C的坐标是______ .
16.如图,已知坐标(1,0),(1,1),(﹣1,1),(﹣1,﹣1),(2,﹣1),…,则点的坐标为 .
三、解答题
17.如图,在直角坐标系中:
(1)写出△ABC各顶点的坐标;
(2)求△ABC的面积.
18.在平面直角坐标系中,已知A(2,a+3),B(b,b-3).
(1)当点A在第一象限的角平分线上时,求a的值;
(2)当点B到x轴的距离是它到y轴距离的2倍时,求点B所在的象限.
19.在由边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,四边形ABCD是格点四边形(顶点为网格线的交点).
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
20.如图,已知A(-2,3)、B(4,3)、C(-1,-3)
(1)求点C到x轴的距离;
(2)求△ABC的面积;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
21.如图,在下面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由?
22.如图1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+| b-3|=0,线段AB交y轴于F点.
(1)求点A、B的坐标.
(2)求点F的坐标;
(3)点P为坐标轴上一点,若△ABP的面积和△ABC的面积相等,求出P点坐标.
参考答案
1.D
【解析】试题解析:点P在第三象限,
由到x轴的距离为2,到y轴的距离为3,得
( 3, 2),
故选D.
2.D
【解析】分析:根据平行于x轴的直线上的点的纵坐标相等求出,再根据求出,然后写出点N的坐标即可.
详解:∵点M(3, 2)与点N(a,b)在同一条平行于x轴的直线上,
∴
∵
∴ 或,
∴点N的坐标为(4, 2)或(2, 2).
故选D.
点睛:考查图形与坐标,主要利用了平行于x轴的直线上的点的纵坐标相同,难点在于要分类讨论.
3.C
【解析】分析:根据题中所给的点的位置,可以确定点的纵横坐标的符号,结合其到坐标轴的距离得到它的坐标.
详解:设A(x,y),由点A在第二象限,
所以x<0,y>0.
因为点A到x轴、y轴的距离分别为1、4,
所以点A的坐标为(-4,1),故选C.
点睛:本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度是解题的关键.
4.B
【解析】分析:本题可在画出图后,根据矩形的性质,得知第四个顶点的横坐标应为3,纵坐标应为2.
详解:如图可知第四个顶点为:
即:(3,2).
故选B.
点睛:本题考查学生的动手能力,画出图后可很快得到答案.
5.C
【解析】分析:根据坐标及x轴∥m,y轴∥n确定坐标轴的位置,即可判断点C所在象限,据此可得.
详解:如图,由A(4,2)、B( 2, 2)知BD=6、AD=4,
∵x轴∥m,y轴∥n,
∴x轴为AD中垂线、y轴过点E,且
由图可知点C在第四象限,C选项符合题意,
故选C.
点睛:考查图形与坐标,关键是确定坐标轴的位置.
6.B
【解析】分析:根据一号暗堡和四号暗堡的坐标可知:这两个暗堡的横坐标一正一负,从水平方向来看,原点要在两暗堡之间;两个暗堡的纵坐标均为正,从竖直方向来看,原点在两暗堡下,结合图形即可确定出原点的位置.
详解:由一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,4),可知:
原点要在两暗堡之间向下的位置,即敌军指挥部的坐标(0,0)大约在点B的位置.
故选B.
点睛:考查了图形与坐标,平面直角坐标系的点和有序数对一一对应,记住每个象限内的点的坐标特征和坐标轴上点的坐标特征.
7.C
【解析】分析:AB∥x轴,说明点A,B的纵坐标相等,再点A的坐标和AB的长求点B的坐标.
详解:因为AB∥x轴,A的坐标为(1,3),所以设B(b,3),
因为AB=5,所以|b-1|=5,解得b=-4或b=6.
即B的坐标为(-4,3)或(6,3).
故选C.
点睛:坐标平面内,平行于x轴的直线上的点的纵坐标相等,平行于y轴的直线上的点的横坐标相等,反之也成立;平行于x轴上的两个点的可表示为(a,y),(b,y),则这两点间的距离为|a-b|,平行于y轴上的两个点的可表示为(x,a),(x,b),则这两点间的距离为|a-b|.
8.B
【解析】根据三角形的面积公式和已知条件,由三角形的面积=×4×|OB|,三角形面积为2,可得|OB|=1,因此可求得点B为(1,0)或(-1,0).
故选:B.
点睛:此题主要考查了平面图形与坐标的关系,利用三角形的面积求出OB的长是关键,特别是要明确注意:在x轴上到原点的距离为一个定值的点有两个.
9.C
【解析】解:∵正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,∴点B的横坐标为:﹣1+4=3,纵坐标为:1,∴点B的坐标为(3,1),∴点C的横坐标为:3,纵坐标为:1+4=5,∴点C的坐标为(3,5).故选C.
点睛:本题考查坐标与图形性质,解题的关键是明确正方形的各条边相等,能根据图形找出它们之间的关系.
10.(3,-1).
【解析】分析:
根据图形和点A、B的坐标画出符合题意的坐标系,根据所画坐标系结合已知条件即可求得点C的坐标.
详解:
如下图,由点A、B的坐标分别为(0,-2),(1,1),建立如图所示的坐标系,
由图可得:点C的坐标为(3,-1).
故答案为:(3,-1).
点睛:“根据点A、B的坐标分别为(0,-2),(1,1),建立如图所示的坐标系”是正确解答本题的关键.
11.3
【解析】分析:首先,根据题意画出,然后,根据三角形的面积计算公式,确定底长和高,代入解答出即可.
详解:如图,根据题意得,
△ABO的底长OB为2,高为3,
∴
故答案为:
点睛:考查了图形与坐标以及三角形的面积公式,可以画出图形,考查了学生数学结合能力.
12.(2,4)
【解析】建立平面直角坐标系如图所示:
则C馆所在地用坐标表示为(2,4),
故答案为:(2,4).
13.2.
【解析】长方形面积为2.
故答案为2.
14.7,8;9,3;3,4
【解析】解:根据题意得:B(7,8),C(9,3),D(3,4).
故答案为:7,8;9,3;3,4.
15. (1,2) (-3,4)
【解析】试题解析: 若平行于轴, 平行于轴,
则点的横坐标等于点的横坐标,点的纵坐标等于点的纵坐标.
点的坐标为:
若平行于轴, 平行于轴,
则点的横坐标等于点的横坐标,点的纵坐标等于点的纵坐标.
点的坐标为:
故答案为:
16.(505,505)
【解析】分析:根据题意可得各个点分别位于象限的角平分线上(A1和第四象限内的点除外),逐步探索出下标和个点坐标之间的关系,总结出规律,根据规律推理点的坐标.
详解:通过观察可得数字是4的倍数余2的点在第一象限,
∵
∴点在第一象限,
是第一个点,
是第二个点,
是第三个点,
是第三象限的第504个点,
∴的坐标为(505,505),
故答案为:(505,505).
点睛:属于规律型,考查点的坐标,首先确定象限,再找出点之间的规律.
17.(1)A(5,7),B(1,1),C(8,3);(2)S△ABC=17.
【解析】分析:(1)由图形可得;
(2)根据三角形面积公式列式计算即可.
详解:(1)由题图可得A(5,7),B(1,1),C(8,3);
(2)S△ABC=6×7﹣×6×4﹣×3×4﹣×2×7=17.
点睛:本题主要考查坐标与图形性质,熟练掌握坐标系中三角形面积的求法是解题关键.
18.(1) a=-1;(2) 当b=-3时,点B(-3,-6)在第三象限;当b=1时,点B(1,-2)在第四象限.
【解析】分析:(1)根据第一象限角平分线上的点的横坐标与纵坐标相等列方程求解即可;
(2)根据题意列出绝对值方程,求出b的值,再求出点B的坐标,然后根据各象限内点的坐标特征解答.
详解:
(1)由题意得a+3=2,解得a=-1.
(2)由题意得|b-3|=2|b|,解得b=-3或b=1.
当b=-3时,b-3=-6,点B(-3,-6)在第三象限;
当b=1时,b-3=-2,点B(1,-2)在第四象限.
点睛:考查了点的坐标,主要利用了第一象限角平分线上点的坐标特征以及点到坐标轴的距离的表示.
19.(1)A(4,1),B(0,0),C(-2,3),D(2,5);(2) 17.
【解析】【分析】(1)根据图形结合坐标系写出各点坐标即可;
(2)利用长方形的面积减去四个顶点上三角形的面积即可.
【详解】(1)A(4,1),B(0,0),C(-2,3),D(2,5);
(2)四边形ABCD的面积为:5×6-×2×3-×2×4-×2×4-×1×4=17.
【点睛】本题考查了平面直角坐标系,点的坐标,四边形的面积等,结合网格特点以及平面直角坐标系的特征确定点的坐标是解题的关键.
20.(1)点C到x轴的距离为3;(2)18;(3)P点的坐标为(0,5)或(0,1).
【解析】分析: (1)点C的纵坐标的绝对值就是点C到x轴的距离解答;
(2)根据三角形的面积公式列式进行计算即可求解;
(3)设点P的坐标为(0,y),根据△ABP的面积为6,A(-2,3)、B(4,3),所以
×6×|x 3|=6,即|x-3|=2,所以x=5或x=1,即可解答.
详解:
(1)∵C(-1,-3),
∴|-3|=3,
∴点C到x轴的距离为3;
(2)∵A(-2,3)、B(4,3)、C(-1,-3)
∴AB=4-(-2) =6,点C到边AB的距离为:3-(-3) =6,
∴△ABC的面积为:6×6÷2=18.
(3)设点P的坐标为(0,y),
∵△ABP的面积为6,A(-2,3)、B(4,3),
∴×6×|x 3|=6,
∴|x-3|=2,
∴x=5或x=1,
∴P点的坐标为(0,5)或(0,1).
点睛: 本题考查了坐标与图形,解决本题的关键是利用数形结合的思想.
21.(1);(2) ;(3)P(-3,) .
【解析】分析:(1)将A,B,C坐标在直角坐标系中表示出来,由三角形面积公式即可求解,(2)因为P在第二象限,将四边形ABOP的面积表示成三角形APO和三角形AOB的面积和,即可求解,(3)当四边形ABOP的面积与△ABC的面积相等时,即3-m=6,得m=-3,即可进行求解.
详解:(1)已知点A(0,2),B(3,0),C(3,4),
过A点作BC边上的高,交BC于点H,
则三角形ABC的面积为:S=BC AH=×4×3=6;
(2)四边形ABOP的面积可以看作是△APO和△AOB的面积和,
∵P在第二象限,∴m<0,SAPOB=S△AOB+SAPO=×2×3+×(-m)×2=3-m.
故四边形ABOP的面积为3-m;
(3)当四边形ABOP的面积与△ABC的面积相等时,
即3-m=6,得m=-3,
此时P点坐标为:(-3,),
存在P点,使四边形ABOP的面积与△ABC的面积相等.
点睛:本题考查了坐标与图形性质及三角形的面积公式,难度较大,关键根据题意画出图形,认真分析解答.
22.(1)A(-3,0),B(3,3)(2)(0,)(3)(0,5);(0,-2);(4,0);(-10,0)
【解析】分析:(1)根据非负数的性质可得a+b=0,a-b+6=0,解得a=-3,b=3,即可得到点A和B的坐标;(2)连结OB,如图,设F(0,t),根据△AOF的面积+△BOF的面积=△AOB的面积可得×3×t+×t×3=×3×3,解方程求得t值,即可得点F的坐标;(3)根据三角形的面积公式计算△ABC的面积为,分点P在y轴上和点P在x轴上两种情况求点P的坐标.
详解:
(1)∵(a+b)2+|a-b+6|=0,
∴a+b=0,a-b+6=0,
∴a=-3,b=3,
∴A(-3,0),B(3,3);
(2)连结OB,如图,
设F(0,t),
∵△AOF的面积+△BOF的面积=△AOB的面积,
∴×3×t+×t×3=×3×3,
解得t=,
∴F点坐标为(0,);
(3)△ABC的面积=×7×3=,
当P点在y轴上时,设P(0,y),
∵△ABP的三角形=△APF的面积+△BPF的面积,
∴ |y-| 3+ |y-| 3=,
解得y=10或y=-2,
∴此时P点坐标为(0,5)或(0,-2);
当P点在x轴上时,设P(x,0),则
|x+3| 3=,解得x=-10或x=4,
∴此时P点坐标为(-10,0)或(4,0),
综上所述,满足条件的P点坐标为(0,5);(0,-2);(4,0);(-10,0)
点睛:本题考查了坐标与图形性质,会利用点的坐标求相应线段的长是解决本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
11.1.3坐标与图形性质同步作业
姓名:__________班级:__________考号:__________
一、选择题
1.平面直角坐标系中,若P(m,n)在第三象限且到x轴,y轴的距离分别为2,3,则点P的坐标为( )
A. (-2,3) B. (-2,-3) C. (3,-2) D. (-3,-2)
2.若点M(3,-2)与点N(x、y)在同一条平行于x轴的直线上,且MN=1,则N点的坐标为( )
A. (4,-2) B. (3,-1) C. (3,-1)或(3,-3) D. (4,-2)或(2,-2)
3.在平面直角坐标系中,点A位于第二象限,距x轴1个单位长度,距y轴4个单位长度,则点A的坐标为( )
A. (1,4) B. (-1,4) C. (-4,1) D. (4,-1)
4.在平面直角坐标系中,一个矩形三个顶点的坐标分别为(-1,-1),(-1,2),(3,-1),则第四个顶点的坐标为( )
A. (2,2) B. (3,2) C. (3,3) D. (2,3)
5.如图,直线m⊥ n,在某平面直角坐标系中,x轴∥ m,y轴∥ n,点A的坐标为(4,2),点B的坐标为(﹣2,﹣2),则点C的坐标为( )
A. (2,1) B. (﹣2,1) C. (2,﹣1) D. (﹣2,﹣1)
6.如图所示为某战役潜伏敌人防御工亭坐标地图的碎片,一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,4),由原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大概( )
A. A处 B. B处 C. C处 D. D处
7.平面直角坐标系内,AB∥ x轴,AB=5,点A的坐标为(1,3),则点B的坐标为( )
A. (-4,3) B. (6,3) C. (-4,3)或(6,3) D. (1,-2)或(1,8)
8.已知A(0,4),点B在x轴上,AB与坐标轴围成的三角形面积为2,则点B的坐标为( )
A. (1,0) B. (1,0)或(-1,0) C. (-1,0) D. (0,-1)或(0,1)
9.如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( )
A. (3,1) B. (-1,1) C. (3,5) D. (-1,5)
二、填空题
10.在边长为1的正方形网格中,如图所示,△ABC中,AB=AC,若点A的坐标为(0,-2),点B的坐标为(1,1),则点C的坐标为__________.
11.在平面直角坐标系中,若A点坐标为(﹣3,3),B点坐标为(2,0),则△ABO的面积为_______
12.如图是某植物园的平面图,图中A馆所在地用坐标表示为(1,0),B馆所在地用坐标表示为(-3,-1),那么C馆所在地用坐标表示为_______.
13.如图,长方形ABOC在直角坐标系中,点A的坐标为(–2,1),则长方形的面积等于 ﹒
14.如图,若四边形ABCD的顶点A可表示为A(3,8),则顶点B,C,D可以表示为B(________)、C(________)、D(________).
15.已知点A(-3,2),点B(1,4),
(1)若CA平行于x轴,BC平行于y轴,则点C的坐标是______ ;
(2)若CA平行于y轴,BC平行于x轴,则点C的坐标是______ .
16.如图,已知坐标(1,0),(1,1),(﹣1,1),(﹣1,﹣1),(2,﹣1),…,则点的坐标为 .
三、解答题
17.如图,在直角坐标系中:
(1)写出△ABC各顶点的坐标;
(2)求△ABC的面积.
18.在平面直角坐标系中,已知A(2,a+3),B(b,b-3).
(1)当点A在第一象限的角平分线上时,求a的值;
(2)当点B到x轴的距离是它到y轴距离的2倍时,求点B所在的象限.
19.在由边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,四边形ABCD是格点四边形(顶点为网格线的交点).
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
20.如图,已知A(-2,3)、B(4,3)、C(-1,-3)
(1)求点C到x轴的距离;
(2)求△ABC的面积;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
21.如图,在下面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由?
22.如图1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+| b-3|=0,线段AB交y轴于F点.
(1)求点A、B的坐标.
(2)求点F的坐标;
(3)点P为坐标轴上一点,若△ABP的面积和△ABC的面积相等,求出P点坐标.
参考答案
1.D
【解析】试题解析:点P在第三象限,
由到x轴的距离为2,到y轴的距离为3,得
( 3, 2),
故选D.
2.D
【解析】分析:根据平行于x轴的直线上的点的纵坐标相等求出,再根据求出,然后写出点N的坐标即可.
详解:∵点M(3, 2)与点N(a,b)在同一条平行于x轴的直线上,
∴
∵
∴ 或,
∴点N的坐标为(4, 2)或(2, 2).
故选D.
点睛:考查图形与坐标,主要利用了平行于x轴的直线上的点的纵坐标相同,难点在于要分类讨论.
3.C
【解析】分析:根据题中所给的点的位置,可以确定点的纵横坐标的符号,结合其到坐标轴的距离得到它的坐标.
详解:设A(x,y),由点A在第二象限,
所以x<0,y>0.
因为点A到x轴、y轴的距离分别为1、4,
所以点A的坐标为(-4,1),故选C.
点睛:本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度是解题的关键.
4.B
【解析】分析:本题可在画出图后,根据矩形的性质,得知第四个顶点的横坐标应为3,纵坐标应为2.
详解:如图可知第四个顶点为:
即:(3,2).
故选B.
点睛:本题考查学生的动手能力,画出图后可很快得到答案.
5.C
【解析】分析:根据坐标及x轴∥m,y轴∥n确定坐标轴的位置,即可判断点C所在象限,据此可得.
详解:如图,由A(4,2)、B( 2, 2)知BD=6、AD=4,
∵x轴∥m,y轴∥n,
∴x轴为AD中垂线、y轴过点E,且
由图可知点C在第四象限,C选项符合题意,
故选C.
点睛:考查图形与坐标,关键是确定坐标轴的位置.
6.B
【解析】分析:根据一号暗堡和四号暗堡的坐标可知:这两个暗堡的横坐标一正一负,从水平方向来看,原点要在两暗堡之间;两个暗堡的纵坐标均为正,从竖直方向来看,原点在两暗堡下,结合图形即可确定出原点的位置.
详解:由一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,4),可知:
原点要在两暗堡之间向下的位置,即敌军指挥部的坐标(0,0)大约在点B的位置.
故选B.
点睛:考查了图形与坐标,平面直角坐标系的点和有序数对一一对应,记住每个象限内的点的坐标特征和坐标轴上点的坐标特征.
7.C
【解析】分析:AB∥x轴,说明点A,B的纵坐标相等,再点A的坐标和AB的长求点B的坐标.
详解:因为AB∥x轴,A的坐标为(1,3),所以设B(b,3),
因为AB=5,所以|b-1|=5,解得b=-4或b=6.
即B的坐标为(-4,3)或(6,3).
故选C.
点睛:坐标平面内,平行于x轴的直线上的点的纵坐标相等,平行于y轴的直线上的点的横坐标相等,反之也成立;平行于x轴上的两个点的可表示为(a,y),(b,y),则这两点间的距离为|a-b|,平行于y轴上的两个点的可表示为(x,a),(x,b),则这两点间的距离为|a-b|.
8.B
【解析】根据三角形的面积公式和已知条件,由三角形的面积=×4×|OB|,三角形面积为2,可得|OB|=1,因此可求得点B为(1,0)或(-1,0).
故选:B.
点睛:此题主要考查了平面图形与坐标的关系,利用三角形的面积求出OB的长是关键,特别是要明确注意:在x轴上到原点的距离为一个定值的点有两个.
9.C
【解析】解:∵正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,∴点B的横坐标为:﹣1+4=3,纵坐标为:1,∴点B的坐标为(3,1),∴点C的横坐标为:3,纵坐标为:1+4=5,∴点C的坐标为(3,5).故选C.
点睛:本题考查坐标与图形性质,解题的关键是明确正方形的各条边相等,能根据图形找出它们之间的关系.
10.(3,-1).
【解析】分析:
根据图形和点A、B的坐标画出符合题意的坐标系,根据所画坐标系结合已知条件即可求得点C的坐标.
详解:
如下图,由点A、B的坐标分别为(0,-2),(1,1),建立如图所示的坐标系,
由图可得:点C的坐标为(3,-1).
故答案为:(3,-1).
点睛:“根据点A、B的坐标分别为(0,-2),(1,1),建立如图所示的坐标系”是正确解答本题的关键.
11.3
【解析】分析:首先,根据题意画出,然后,根据三角形的面积计算公式,确定底长和高,代入解答出即可.
详解:如图,根据题意得,
△ABO的底长OB为2,高为3,
∴
故答案为:
点睛:考查了图形与坐标以及三角形的面积公式,可以画出图形,考查了学生数学结合能力.
12.(2,4)
【解析】建立平面直角坐标系如图所示:
则C馆所在地用坐标表示为(2,4),
故答案为:(2,4).
13.2.
【解析】长方形面积为2.
故答案为2.
14.7,8;9,3;3,4
【解析】解:根据题意得:B(7,8),C(9,3),D(3,4).
故答案为:7,8;9,3;3,4.
15. (1,2) (-3,4)
【解析】试题解析: 若平行于轴, 平行于轴,
则点的横坐标等于点的横坐标,点的纵坐标等于点的纵坐标.
点的坐标为:
若平行于轴, 平行于轴,
则点的横坐标等于点的横坐标,点的纵坐标等于点的纵坐标.
点的坐标为:
故答案为:
16.(505,505)
【解析】分析:根据题意可得各个点分别位于象限的角平分线上(A1和第四象限内的点除外),逐步探索出下标和个点坐标之间的关系,总结出规律,根据规律推理点的坐标.
详解:通过观察可得数字是4的倍数余2的点在第一象限,
∵
∴点在第一象限,
是第一个点,
是第二个点,
是第三个点,
是第三象限的第504个点,
∴的坐标为(505,505),
故答案为:(505,505).
点睛:属于规律型,考查点的坐标,首先确定象限,再找出点之间的规律.
17.(1)A(5,7),B(1,1),C(8,3);(2)S△ABC=17.
【解析】分析:(1)由图形可得;
(2)根据三角形面积公式列式计算即可.
详解:(1)由题图可得A(5,7),B(1,1),C(8,3);
(2)S△ABC=6×7﹣×6×4﹣×3×4﹣×2×7=17.
点睛:本题主要考查坐标与图形性质,熟练掌握坐标系中三角形面积的求法是解题关键.
18.(1) a=-1;(2) 当b=-3时,点B(-3,-6)在第三象限;当b=1时,点B(1,-2)在第四象限.
【解析】分析:(1)根据第一象限角平分线上的点的横坐标与纵坐标相等列方程求解即可;
(2)根据题意列出绝对值方程,求出b的值,再求出点B的坐标,然后根据各象限内点的坐标特征解答.
详解:
(1)由题意得a+3=2,解得a=-1.
(2)由题意得|b-3|=2|b|,解得b=-3或b=1.
当b=-3时,b-3=-6,点B(-3,-6)在第三象限;
当b=1时,b-3=-2,点B(1,-2)在第四象限.
点睛:考查了点的坐标,主要利用了第一象限角平分线上点的坐标特征以及点到坐标轴的距离的表示.
19.(1)A(4,1),B(0,0),C(-2,3),D(2,5);(2) 17.
【解析】【分析】(1)根据图形结合坐标系写出各点坐标即可;
(2)利用长方形的面积减去四个顶点上三角形的面积即可.
【详解】(1)A(4,1),B(0,0),C(-2,3),D(2,5);
(2)四边形ABCD的面积为:5×6-×2×3-×2×4-×2×4-×1×4=17.
【点睛】本题考查了平面直角坐标系,点的坐标,四边形的面积等,结合网格特点以及平面直角坐标系的特征确定点的坐标是解题的关键.
20.(1)点C到x轴的距离为3;(2)18;(3)P点的坐标为(0,5)或(0,1).
【解析】分析: (1)点C的纵坐标的绝对值就是点C到x轴的距离解答;
(2)根据三角形的面积公式列式进行计算即可求解;
(3)设点P的坐标为(0,y),根据△ABP的面积为6,A(-2,3)、B(4,3),所以
×6×|x 3|=6,即|x-3|=2,所以x=5或x=1,即可解答.
详解:
(1)∵C(-1,-3),
∴|-3|=3,
∴点C到x轴的距离为3;
(2)∵A(-2,3)、B(4,3)、C(-1,-3)
∴AB=4-(-2) =6,点C到边AB的距离为:3-(-3) =6,
∴△ABC的面积为:6×6÷2=18.
(3)设点P的坐标为(0,y),
∵△ABP的面积为6,A(-2,3)、B(4,3),
∴×6×|x 3|=6,
∴|x-3|=2,
∴x=5或x=1,
∴P点的坐标为(0,5)或(0,1).
点睛: 本题考查了坐标与图形,解决本题的关键是利用数形结合的思想.
21.(1);(2) ;(3)P(-3,) .
【解析】分析:(1)将A,B,C坐标在直角坐标系中表示出来,由三角形面积公式即可求解,(2)因为P在第二象限,将四边形ABOP的面积表示成三角形APO和三角形AOB的面积和,即可求解,(3)当四边形ABOP的面积与△ABC的面积相等时,即3-m=6,得m=-3,即可进行求解.
详解:(1)已知点A(0,2),B(3,0),C(3,4),
过A点作BC边上的高,交BC于点H,
则三角形ABC的面积为:S=BC AH=×4×3=6;
(2)四边形ABOP的面积可以看作是△APO和△AOB的面积和,
∵P在第二象限,∴m<0,SAPOB=S△AOB+SAPO=×2×3+×(-m)×2=3-m.
故四边形ABOP的面积为3-m;
(3)当四边形ABOP的面积与△ABC的面积相等时,
即3-m=6,得m=-3,
此时P点坐标为:(-3,),
存在P点,使四边形ABOP的面积与△ABC的面积相等.
点睛:本题考查了坐标与图形性质及三角形的面积公式,难度较大,关键根据题意画出图形,认真分析解答.
22.(1)A(-3,0),B(3,3)(2)(0,)(3)(0,5);(0,-2);(4,0);(-10,0)
【解析】分析:(1)根据非负数的性质可得a+b=0,a-b+6=0,解得a=-3,b=3,即可得到点A和B的坐标;(2)连结OB,如图,设F(0,t),根据△AOF的面积+△BOF的面积=△AOB的面积可得×3×t+×t×3=×3×3,解方程求得t值,即可得点F的坐标;(3)根据三角形的面积公式计算△ABC的面积为,分点P在y轴上和点P在x轴上两种情况求点P的坐标.
详解:
(1)∵(a+b)2+|a-b+6|=0,
∴a+b=0,a-b+6=0,
∴a=-3,b=3,
∴A(-3,0),B(3,3);
(2)连结OB,如图,
设F(0,t),
∵△AOF的面积+△BOF的面积=△AOB的面积,
∴×3×t+×t×3=×3×3,
解得t=,
∴F点坐标为(0,);
(3)△ABC的面积=×7×3=,
当P点在y轴上时,设P(0,y),
∵△ABP的三角形=△APF的面积+△BPF的面积,
∴ |y-| 3+ |y-| 3=,
解得y=10或y=-2,
∴此时P点坐标为(0,5)或(0,-2);
当P点在x轴上时,设P(x,0),则
|x+3| 3=,解得x=-10或x=4,
∴此时P点坐标为(-10,0)或(4,0),
综上所述,满足条件的P点坐标为(0,5);(0,-2);(4,0);(-10,0)
点睛:本题考查了坐标与图形性质,会利用点的坐标求相应线段的长是解决本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
