2017—2018学年八年级数学上册期末检测卷含答案(新版)冀教版
文档属性
| 名称 | 2017—2018学年八年级数学上册期末检测卷含答案(新版)冀教版 | 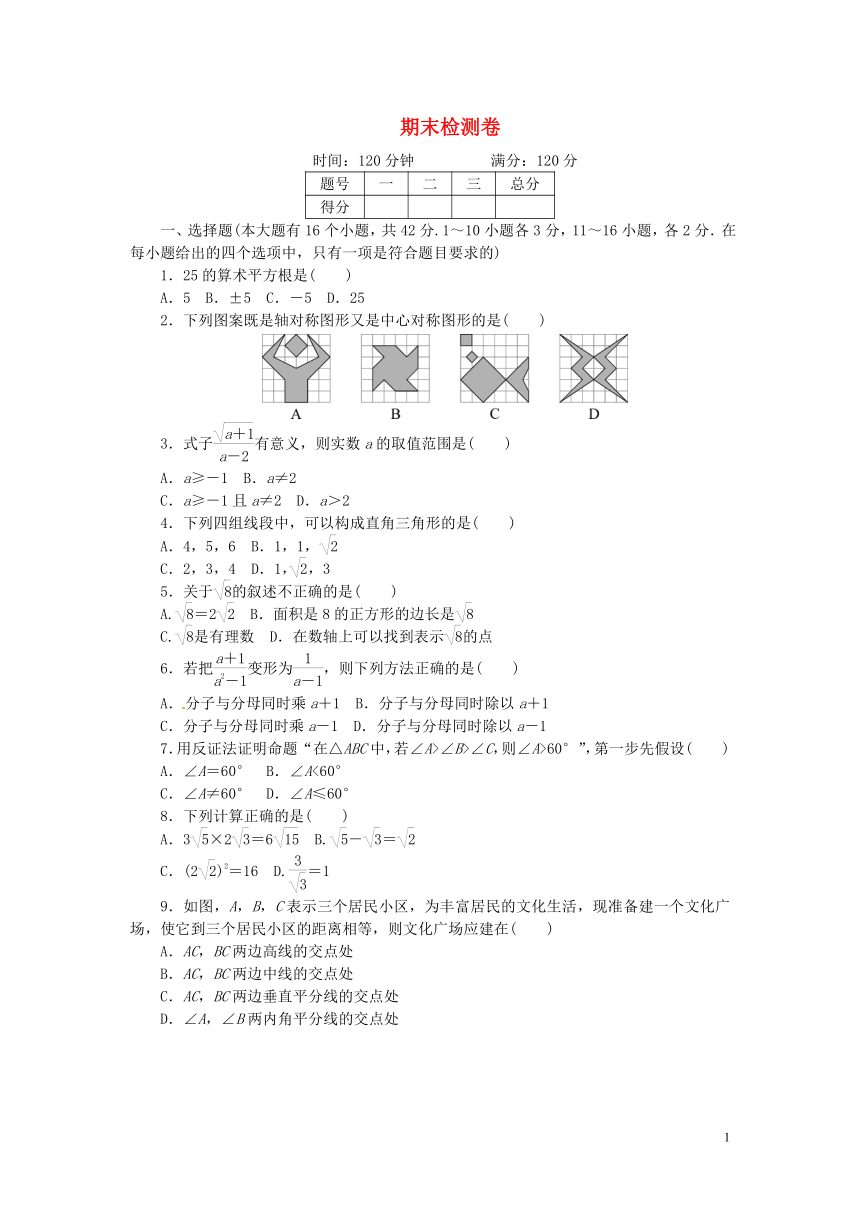 | |
| 格式 | zip | ||
| 文件大小 | 131.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-16 15:10:23 | ||
图片预览




文档简介
期末检测卷
时间:120分钟 满分:120分
题号
一
二
三
总分
得分
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题,各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.25的算术平方根是( )
A.5 B.±5 C.-5 D.25
2.下列图案既是轴对称图形又是中心对称图形的是( )
3.式子有意义,则实数a的取值范围是( )
A.a≥-1 B.a≠2
C.a≥-1且a≠2 D.a>2
4.下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.1,1,
C.2,3,4 D.1,,3
5.关于的叙述不正确的是( )
A.=2 B.面积是8的正方形的边长是
C.是有理数 D.在数轴上可以找到表示的点
6.若把变形为,则下列方法正确的是( )
A.分子与分母同时乘a+1 B.分子与分母同时除以a+1
C.分子与分母同时乘a-1 D.分子与分母同时除以a-1
7.用反证法证明命题“在△ABC中,若∠A>∠B>∠C,则∠A>60°”,第一步先假设( )
A.∠A=60° B.∠A<60°
C.∠A≠60° D.∠A≤60°
8.下列计算正确的是( )
A.3×2=6 B.-=
C.(2)2=16 D.=1
9.如图,A,B,C表示三个居民小区,为丰富居民的文化生活,现准备建一个文化广场,使它到三个居民小区的距离相等,则文化广场应建在( )
A.AC,BC两边高线的交点处
B.AC,BC两边中线的交点处
C.AC,BC两边垂直平分线的交点处
D.∠A,∠B两内角平分线的交点处
第9题图 第12题图
10.下列整数中,与最接近的是( )
A.2 B.3 C.4 D.5
11.下列命题:①若a2=b,则a=;②角平分线上的点到角两边的距离相等;③全等三角形的周长相等;④等边三角形的三个内角相等.它们的逆命题一定成立的有( )
A.①②③④ B.①②④ C.②③④ D.②④
12.如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
A.18cm B.22cm C.24cm D.26cm
13.如果a2+2a-1=0,那么代数式·的值是( )
A.-3 B.-1 C.1 D.3
14.如图,在△ABC和△CED中,已知AC=CD,AC⊥CD,∠B=∠E=90°,则下列结论不正确的是( )
A.∠A与∠D互为余角 B.∠A=∠2
C.△ABC≌△CED D.∠1=∠2
第14题图 第16题图
15.关于x的方程=2+无解,则m的值为( )
A.-5 B.-8 C.-2 D.5
16.如图,用三角尺按下面方法操作:在已知∠AOB的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,连接MN.则下面的结论:①PM=PN;②MP=OP;③∠AOP=∠BOP;④△MON是等边三角形.正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题有3个小题,共10分,17~18小题各3分,19小题有2个空,每空2分.把答案写在题中横线上)
17.若实数a,b满足(a-3)2+|b-6|=0,则以a、b的值为边长的等腰三角形的周长为________.
18.如图,点B,F,C,E在同一条直线上,BF=CE,AB∥DE.若证明△ABC≌△DEF,还需添加一个条件是__________.
第18题图 第19题图
19.如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去.记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an(n为正整数),则a4=________;根据以上规律求出an=________.
三、解答题(本大题有7个小题,共68分.解答应写出文字说明,证明过程或演算步骤)
20.(8分)(1)计算:×-÷--(+1)2.
(2)如图,在△ABC中,∠A>∠B.
①作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);
②在①的条件下,连接AE,若∠B=50°,则∠AEC的度数是________.
21.(9分)先化简,再求值:÷,其中x=-2+2(π-3)0.
22.(9分)先阅读下面的文字,然后解答问题.
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用-1表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
由此我们还可以得到一个真命题:如果=x+y,其中x是整数,且0<y<1,那么x=1,y=-1.
请解答下列问题:
(1)如果-=a+b,其中a是整数,且0<b<1,那么a=________,b=________;
(2)已知2+=m+n,其中m是整数,且0<n<1,求|m-n|的值.
23.(9分)如图,在小正方形组成的网格中有一个四边形图案.
(1)请你分别画出△ABC绕点O顺时针旋转90°的图形,关于点O对称的图形以及逆时针旋转90°的图形,并将它们涂黑;
(2)若网格中每个小正方形的边长为1,旋转后点A的对应点依次为A1,A2,A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.
24.(10分)甲、乙两个工程队计划参与一项工程建设,甲队单独施工20天完成该项工程的,这时乙队加入,两队还需同时施工16天,才能完成该项工程.
(1)若甲队单独施工,需要________天才能完成任务;
(2)若乙队单独施工,需要多少天才能完成该项工程?
(3)若甲队参与该项工程施工的时间不超过30天,则乙队至少施工多少天才能完成该项工程?
25.(11分)如图,等边△ABC中,AB=6,D是AC的中点,E是BC延长线上的一点,CE=CD,DF⊥BE,垂足为F.
(1)求BD的长;
(2)求证:BF=EF;
(3)求△BDE的面积.
26.(12分)已知△ABC中,∠BAC=90°,AB=AC,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作△ADE,使∠DAE=90°,AD=AE,连接CE.
【发现问题】
(1)如图①,当点D在边BC上时,请写出BD和CE之间的数量关系为________,并猜想BC和CE、CD之间的数量关系:__________;
【尝试探究】
(2)如图②,当点D在边BC的延长线上且其他条件不变时,(1)中BC和CE、CD之间存在的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
【拓展延伸】
(3)如图③,当点D在边CB的延长线上且其他条件不变时,若BC=6,CE=2,求线段CD的长.
参考答案与解析
1.A 2.D 3.C 4.B 5.C 6.B 7.D
8.A 9.C 10.B 11.B 12.B 13.C
14.D 15.A 16.B 17.15
18.∠A=∠D(答案不唯一)
19.2(或()3) ()n-1(或)
20.解:(1)原式=×3-3÷-2-(3+2+1)=6-3-2-4-2=-3-2.(4分)
(2)①如图所示.(6分)
②100°(8分)
21.解:原式=÷=÷=·=.(3分)x=-2+2(π-3)0=×4-2×+2=2-+2=+2.(6分)当x=+2时,原式===2.(9分)
22.解:(1)-3 3-(4分)
(2)∵2+=m+n,其中m是整数,且0<n<1,∴m=4,n=-2,(7分)则|m-n|=|4-+2|=6-.(9分)
23.解:(1)如图所示.(3分)
(2)S四边形AA1A2A3=S四边形BB1B2B3-4S△BAA3=(3+5)2-4××3×5=34.故四边形AA1A2A3的面积为34.(6分)
(3)设AB,BC,AC的长分别为c,a,b,则由图可知(a+c)2=4×ac+b2,整理得c2+a2=b2,即AB2+BC2=AC2.这就是著名的勾股定理.(9分)
24.解:(1)60(2分)
(2)设乙队单独施工,需要x天才能完成该项工程,根据题意可得+16×=1,(4分)解得x=40.经检验,x=40是原方程的根.
答:乙队单独施工,需要40天才能完成该项工程.(6分)
(3)设乙队参与施工y天才能完成该项工程,根据题意可得:×30+y×≥1,(8分)解得y≥20.
答:乙队至少施工20天才能完成该项工程.(10分)
25.(1)解:∵BD是等边△ABC的中线,∴BD⊥AC,BD平分AC.(1分)∵AB=6,∴AD=3.(2分)由勾股定理,得BD===3.(4分)
(2)证明:∵BD是等边△ABC的中线,∴BD平分∠ABC,∴∠DBE=∠ABC=30°.(5分)又∵CE=CD,∴∠E=∠CDE,∴∠E=∠ACB=30°.∴∠DBE=∠E.(6分)∴DB=DE.∵DF⊥BE,∴DF为底边BE上的中线.∴BF=EF.(7分)
(3)解:∵CE=CD=3,∴BE=BC+CE=9.(8分)在Rt△DBF中,∵∠DBE=30°,DB=3,∴DF=DB=×3=,(9分)∴△BDE的面积为BE·DF=×9×=.(11分)
26.解:(1)BD=CE BC=CE+CD(2分)
(2)不成立,存在的数量关系为BC=CE-CD.(3分)理由:∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.(4分)在△ABD和△ACE中,∴△ABD≌△ACE(SAS),(5分)∴BD=CE.(6分)又BD=BC+CD,∴CE=BC+CD,∴BC=CE-CD.(7分)
(3)∵∠BAC=∠DAE=90°,∴∠BAC-∠BAE=∠DAE-∠BAE,即∠CAE=∠BAD.(8分)在△ABD和△ACE中,∴△ABD≌△ACE(SAS).(10分)∴BD=CE,∴CD=BC+BD=BC+CE.(11分)∵BC=6,CE=2,CD=6+2=8.(12分)
时间:120分钟 满分:120分
题号
一
二
三
总分
得分
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题,各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.25的算术平方根是( )
A.5 B.±5 C.-5 D.25
2.下列图案既是轴对称图形又是中心对称图形的是( )
3.式子有意义,则实数a的取值范围是( )
A.a≥-1 B.a≠2
C.a≥-1且a≠2 D.a>2
4.下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.1,1,
C.2,3,4 D.1,,3
5.关于的叙述不正确的是( )
A.=2 B.面积是8的正方形的边长是
C.是有理数 D.在数轴上可以找到表示的点
6.若把变形为,则下列方法正确的是( )
A.分子与分母同时乘a+1 B.分子与分母同时除以a+1
C.分子与分母同时乘a-1 D.分子与分母同时除以a-1
7.用反证法证明命题“在△ABC中,若∠A>∠B>∠C,则∠A>60°”,第一步先假设( )
A.∠A=60° B.∠A<60°
C.∠A≠60° D.∠A≤60°
8.下列计算正确的是( )
A.3×2=6 B.-=
C.(2)2=16 D.=1
9.如图,A,B,C表示三个居民小区,为丰富居民的文化生活,现准备建一个文化广场,使它到三个居民小区的距离相等,则文化广场应建在( )
A.AC,BC两边高线的交点处
B.AC,BC两边中线的交点处
C.AC,BC两边垂直平分线的交点处
D.∠A,∠B两内角平分线的交点处
第9题图 第12题图
10.下列整数中,与最接近的是( )
A.2 B.3 C.4 D.5
11.下列命题:①若a2=b,则a=;②角平分线上的点到角两边的距离相等;③全等三角形的周长相等;④等边三角形的三个内角相等.它们的逆命题一定成立的有( )
A.①②③④ B.①②④ C.②③④ D.②④
12.如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
A.18cm B.22cm C.24cm D.26cm
13.如果a2+2a-1=0,那么代数式·的值是( )
A.-3 B.-1 C.1 D.3
14.如图,在△ABC和△CED中,已知AC=CD,AC⊥CD,∠B=∠E=90°,则下列结论不正确的是( )
A.∠A与∠D互为余角 B.∠A=∠2
C.△ABC≌△CED D.∠1=∠2
第14题图 第16题图
15.关于x的方程=2+无解,则m的值为( )
A.-5 B.-8 C.-2 D.5
16.如图,用三角尺按下面方法操作:在已知∠AOB的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,连接MN.则下面的结论:①PM=PN;②MP=OP;③∠AOP=∠BOP;④△MON是等边三角形.正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题有3个小题,共10分,17~18小题各3分,19小题有2个空,每空2分.把答案写在题中横线上)
17.若实数a,b满足(a-3)2+|b-6|=0,则以a、b的值为边长的等腰三角形的周长为________.
18.如图,点B,F,C,E在同一条直线上,BF=CE,AB∥DE.若证明△ABC≌△DEF,还需添加一个条件是__________.
第18题图 第19题图
19.如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去.记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an(n为正整数),则a4=________;根据以上规律求出an=________.
三、解答题(本大题有7个小题,共68分.解答应写出文字说明,证明过程或演算步骤)
20.(8分)(1)计算:×-÷--(+1)2.
(2)如图,在△ABC中,∠A>∠B.
①作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);
②在①的条件下,连接AE,若∠B=50°,则∠AEC的度数是________.
21.(9分)先化简,再求值:÷,其中x=-2+2(π-3)0.
22.(9分)先阅读下面的文字,然后解答问题.
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用-1表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
由此我们还可以得到一个真命题:如果=x+y,其中x是整数,且0<y<1,那么x=1,y=-1.
请解答下列问题:
(1)如果-=a+b,其中a是整数,且0<b<1,那么a=________,b=________;
(2)已知2+=m+n,其中m是整数,且0<n<1,求|m-n|的值.
23.(9分)如图,在小正方形组成的网格中有一个四边形图案.
(1)请你分别画出△ABC绕点O顺时针旋转90°的图形,关于点O对称的图形以及逆时针旋转90°的图形,并将它们涂黑;
(2)若网格中每个小正方形的边长为1,旋转后点A的对应点依次为A1,A2,A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.
24.(10分)甲、乙两个工程队计划参与一项工程建设,甲队单独施工20天完成该项工程的,这时乙队加入,两队还需同时施工16天,才能完成该项工程.
(1)若甲队单独施工,需要________天才能完成任务;
(2)若乙队单独施工,需要多少天才能完成该项工程?
(3)若甲队参与该项工程施工的时间不超过30天,则乙队至少施工多少天才能完成该项工程?
25.(11分)如图,等边△ABC中,AB=6,D是AC的中点,E是BC延长线上的一点,CE=CD,DF⊥BE,垂足为F.
(1)求BD的长;
(2)求证:BF=EF;
(3)求△BDE的面积.
26.(12分)已知△ABC中,∠BAC=90°,AB=AC,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作△ADE,使∠DAE=90°,AD=AE,连接CE.
【发现问题】
(1)如图①,当点D在边BC上时,请写出BD和CE之间的数量关系为________,并猜想BC和CE、CD之间的数量关系:__________;
【尝试探究】
(2)如图②,当点D在边BC的延长线上且其他条件不变时,(1)中BC和CE、CD之间存在的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
【拓展延伸】
(3)如图③,当点D在边CB的延长线上且其他条件不变时,若BC=6,CE=2,求线段CD的长.
参考答案与解析
1.A 2.D 3.C 4.B 5.C 6.B 7.D
8.A 9.C 10.B 11.B 12.B 13.C
14.D 15.A 16.B 17.15
18.∠A=∠D(答案不唯一)
19.2(或()3) ()n-1(或)
20.解:(1)原式=×3-3÷-2-(3+2+1)=6-3-2-4-2=-3-2.(4分)
(2)①如图所示.(6分)
②100°(8分)
21.解:原式=÷=÷=·=.(3分)x=-2+2(π-3)0=×4-2×+2=2-+2=+2.(6分)当x=+2时,原式===2.(9分)
22.解:(1)-3 3-(4分)
(2)∵2+=m+n,其中m是整数,且0<n<1,∴m=4,n=-2,(7分)则|m-n|=|4-+2|=6-.(9分)
23.解:(1)如图所示.(3分)
(2)S四边形AA1A2A3=S四边形BB1B2B3-4S△BAA3=(3+5)2-4××3×5=34.故四边形AA1A2A3的面积为34.(6分)
(3)设AB,BC,AC的长分别为c,a,b,则由图可知(a+c)2=4×ac+b2,整理得c2+a2=b2,即AB2+BC2=AC2.这就是著名的勾股定理.(9分)
24.解:(1)60(2分)
(2)设乙队单独施工,需要x天才能完成该项工程,根据题意可得+16×=1,(4分)解得x=40.经检验,x=40是原方程的根.
答:乙队单独施工,需要40天才能完成该项工程.(6分)
(3)设乙队参与施工y天才能完成该项工程,根据题意可得:×30+y×≥1,(8分)解得y≥20.
答:乙队至少施工20天才能完成该项工程.(10分)
25.(1)解:∵BD是等边△ABC的中线,∴BD⊥AC,BD平分AC.(1分)∵AB=6,∴AD=3.(2分)由勾股定理,得BD===3.(4分)
(2)证明:∵BD是等边△ABC的中线,∴BD平分∠ABC,∴∠DBE=∠ABC=30°.(5分)又∵CE=CD,∴∠E=∠CDE,∴∠E=∠ACB=30°.∴∠DBE=∠E.(6分)∴DB=DE.∵DF⊥BE,∴DF为底边BE上的中线.∴BF=EF.(7分)
(3)解:∵CE=CD=3,∴BE=BC+CE=9.(8分)在Rt△DBF中,∵∠DBE=30°,DB=3,∴DF=DB=×3=,(9分)∴△BDE的面积为BE·DF=×9×=.(11分)
26.解:(1)BD=CE BC=CE+CD(2分)
(2)不成立,存在的数量关系为BC=CE-CD.(3分)理由:∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.(4分)在△ABD和△ACE中,∴△ABD≌△ACE(SAS),(5分)∴BD=CE.(6分)又BD=BC+CD,∴CE=BC+CD,∴BC=CE-CD.(7分)
(3)∵∠BAC=∠DAE=90°,∴∠BAC-∠BAE=∠DAE-∠BAE,即∠CAE=∠BAD.(8分)在△ABD和△ACE中,∴△ABD≌△ACE(SAS).(10分)∴BD=CE,∴CD=BC+BD=BC+CE.(11分)∵BC=6,CE=2,CD=6+2=8.(12分)
同课章节目录
