1.5 平方差公式课件

课件30张PPT。平方差公式回顾与思考(m+a)(n+b)=用一个多项式的每一项 乘另一个多项式的每一项再把所得的积相加。mn+mb+an+ab =(x+a)(x+b)x2+(a+b)x+ab 这是上一节学习的
一种特殊多项式的乘法—— 两个相同字母的
二项式的乘积 .这就是从本课起要学习的内容． 平 方 差 公 式计算下列各题:=x2?9 ;=1?4a2 ;=x2?16y2 ;=y2?25z2 ;你发现了什么规律？=x2?32 ;=12?(2a)2 ;=x2?(4y)2 ;=y2?(5z)2 .(a+b)(a?b)=a2?b2.两数和与这两数差的积,等于这两数的平方的差.用式子表示，即：初 识 平 方 差 公 式(a+b)(a?b)=a2?b2 (1) 公式左边两个二项式必须是相同两数的和与差相乘； 且左边两括号内的第一项相等、 第二项符号相反
[互为相反数(式)];(2) 公式右边是这两个数的平方差； 即右边是左边括号内的第一项的平方
减去第二项的平方. (3) 公式中的 a和b 可以代表数，
也可以是代数式． 特征
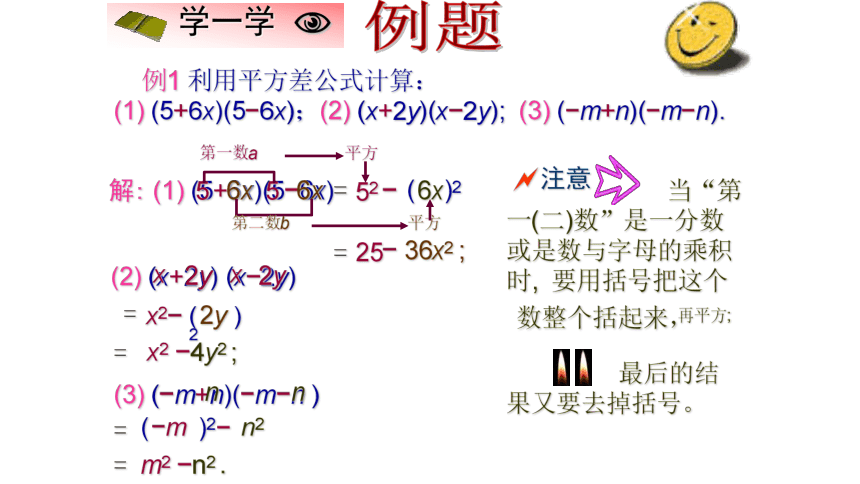
结构｛例题解析例题 例1 利用平方差公式计算：
(1) (5+6x)(5?6x)；(2) (x+2y)(x?2y); (3) (?m+n)(?m?n).解: (1) (5+6x)(5?6x)=55第一数a52? 要用括号把这个数整个括起来， 再平方; ( )26x=25?36x2 ;(2) (x+2y) (x?2y)
=x2?( )22y=x2 ?4y2 ;(3) (?m+n)(?m?n )
=?m( )2?n2=m2 ?n2 .随堂练习(1)(a+2)(a?2)； (2)(3a +2b)(3a?2b) ;1、计算：(3)(?x+1)(?x?1) ; (4)(?4k+3)(?4k?3) .小结本节课你学到了什么?试用语言表述平方差公式 (a+b)(a?b)=x2?b2。应用平方差公式 时要注意一些什么？两数和与这两数差的积，等于它们的平方差。变成公式标准形式后，再用公式。 或提取两“?”号中的“?”号，运用平方差公式时，要紧扣公式的特征，
找出相等的“项”和符号相反的“项”，然后应用公式； 要利用加法交换律，对于不符合平方差公式标准形式者，纠 错 练 习(1) (1+2x)(1?2x)=1?2x2
(2) (2a2+b2)(2a2?b2)=2a4?b4
(3) (3m+2n)(3m?2n)=3m2?2n2本题对公式的直接运用，以加深对公式本质特征的理解． 指出下列计算中的错误： 2x2x第二数被平方时，未添括号。2a22a22a第一 数被平方时，未添括号。3m3m3m2n2n2n第一数与第二数被平方时，
都未添括号。2x拓 展 练 习本题是公式的变式训练，以加深对公式本质特征的理解． 运用平方差公式计算：
(?4a?1)(4a?1)． (用两种方法) ?运用平方差公式时，要紧扣公式的特征，
找出相等的“项”和符号相反的“项”，然后应用公式。 (?4a?1)(4a?1)
==(?1)2 ?(4a)2 = 1?16a2。(?4a?1)(4a?1)= ?(4a+1) (?4a?1)(4a?1)= (4a)2 ?1??[ ] = 1?16a2。( ?4a?1 ) ( 4a ?1 )?1+4a(4a+1) (4a?1)?1?4a(1) (a+b)(?a?b) ；
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 本题是公式的变式训练，以加深对公式本质特征的理解． 下列式子可用平方差公式计算吗? 为什么? 如果能够，怎样计算? (第一个数不完全一样 ) (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(不能) 平方差公式平方差公式： 两数和与这两数差的积，等于它们的平方差。 学习目标
1.会用面积法推导平方差公式，并能运用公式进行简单的运算.
2.用符号运算证明猜想，提高解决问题的能力.
3.提高自己的观察、归纳、概括等能力。
观察与思考1、计算下列各组算式,并观察它们的共同特点： 2、从以上的过程中，你发现了什么规律？
（一个自然数的平方比它相邻两数的积大1.）3、请用字母表示这一规律，你能说明它的正确性吗？自学质疑例题用平方差公式进行简便计算：解：试一试计算：解：原式解：原式试一试解：原式反馈矫正1.下列各式的解法中，哪种简单？解（一）：原式解（二）：原式2.学校有一个边长为 米的正方形花坛，现在要进行改建，将它的一边增加3米，而另一边缩短3米.问改建后的正方形花坛的面积是多少？变式练习(1) 填空x9-x2-3-a-ba3a3x+yz公式的逆用
(1)(x+y)2－(x－y)2 (2)252－242
分析：逆用平方差公式可以使运算简便.
解：(1)(x+y)2－(x－y)2
=［(x+y)+(x－y)］［(x+y)－(x－y)］
=2x·2y
=4xy
(2)252－242
=(25+24)(25－24)
=49
（1）公式的左边是两个二项式的积，在这两个二项式中，有一项完全相同，另一项互为相反数；（2）公式的右边是乘式中两项的平方差，且完全相同的项的平方减去互为相反数的一项的平方；（3）对于形如两数和与这两数差相乘，就可以运用上述公式来计算；1. 平方差公式的内涵：2. 平方差公式的结构特征：在整式的乘法中只有符合公式要求的乘法才能 用公式计算，其余的运算仍按乘法法则进行总结与反思课堂检测
y +zx-yxyx-zzxn+1-1思考题解答：