第十一讲 轴对称、平移与旋转培优竞赛辅导(含答案)
文档属性
| 名称 | 第十一讲 轴对称、平移与旋转培优竞赛辅导(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-22 08:14:55 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第十一讲 轴对称、平移与旋转
一、知识网络
二、知识回顾,自主盘点
(一)轴对称与轴对称图形
1、定义:(1)如果一个图形沿某条 对折,直线两旁的部分能 ,这个图形叫做轴对称图形。
(2)把一个图形沿着某条直线翻折过去,如果它能够与 ,那么就说这两个图形成轴对称,这条直线就是 。
2、特征:轴对称图形的对称轴,是任意一组对应点连线的 。由轴对称变换得到的图形与原图 、 完全相同。
(二)图形的平移
1、定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,平移不改变图形的形状和大小.
两要素: 和 ;
2、特征①:平移后的图形与原来图形的对应线段 且 ,或
②对应角 ;平移后对应点所连的线段 且或 。
③平移不改变图形的形状和大小.
(三)图形旋转
1、定义:旋转是指图形绕着某一个固定点按一定方向(顺时针或逆时针)旋转一定的角度(小于360°),三要素: 、 和 ;
2、特征①图形上的每一个点都绕着旋转中心按同一旋转方向旋转了 大小的角度;
② 对应点到旋转中心的距离 ,对应点与旋转中心所连线段的夹角就是 ③对应线段 ,对应角 ④旋转前后的图形 不变。
(四)中心对称
(1)把一个图形绕着 旋转 度后 能与自身重合,那么这个图形叫做中心对称图形,这个点就是它的 。
(2)把一个图形绕着某一点旋转 ,如果它能与另一个图形 ,那么,我们就说这两个图形成中心对称。
注意:经过对称中心的直线将中心对称图形分为 相同的两个部分。
旋转对称图形可以旋转任意的角度,而中心对称图形必须旋转180°.
(五)图形的全等特征:
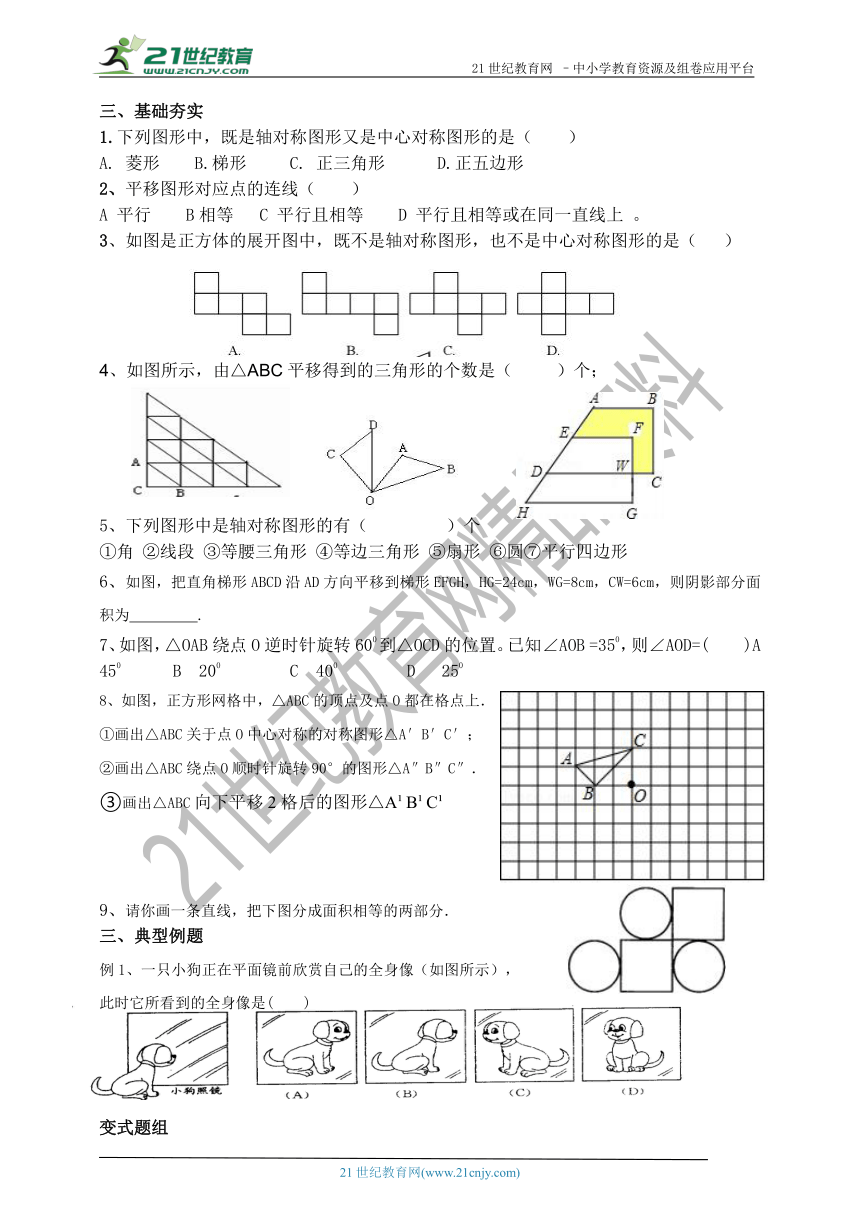
三、基础夯实
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. 菱形 B.梯形 C. 正三角形 D.正五边形
2、平移图形对应点的连线( )
A 平行 B相等 C 平行且相等 D 平行且相等或在同一直线上 。
3、如图是正方体的展开图中,既不是轴对称图形,也不是中心对称图形的是( )
4、如图所示,由△ABC平移得到的三角形的个数是( )个;
5、下列图形中是轴对称图形的有( )个
①角 ②线段 ③等腰三角形 ④等边三角形 ⑤扇形 ⑥圆⑦平行四边形
6、如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,则阴影部分面积为 .
7、如图,△OAB绕点O逆时针旋转600到△OCD的位置。已知∠AOB =350,则∠AOD=( )A 450 B 200 C 400 D 250
8、如图,正方形网格中,△ABC的顶点及点O都在格点上.
①画出△ABC关于点O中心对称的对称图形△A′B′C′;
②画出△ABC绕点O顺时针旋转90°的图形△A″B″C″.
③画出△ABC向下平移2格后的图形△A B C
请你画一条直线,把下图分成面积相等的两部分.
三、典型例题
一只小狗正在平面镜前欣赏自己的全身像(如图所示),
此时它所看到的全身像是( )
变式题组
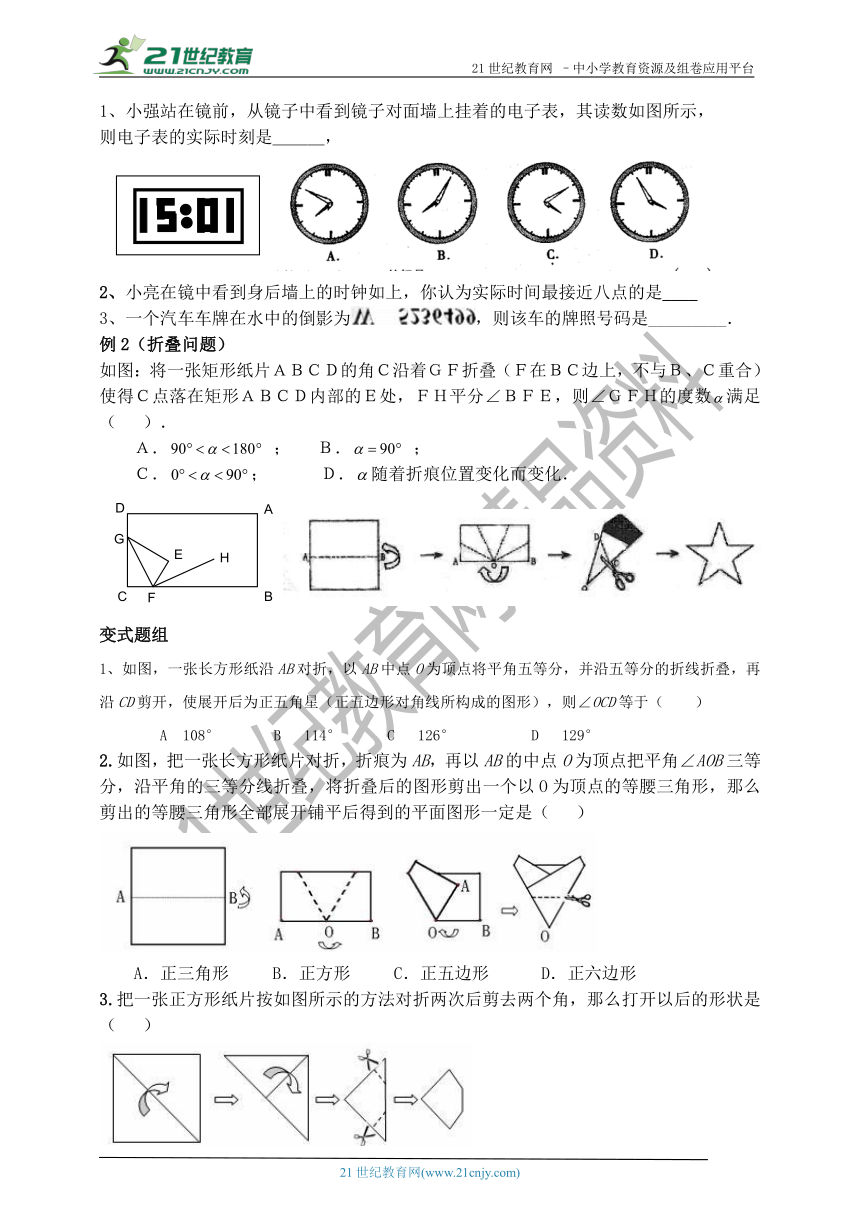
小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,
则电子表的实际时刻是___,
小亮在镜中看到身后墙上的时钟如上,你认为实际时间最接近八点的是____
一个汽车车牌在水中的倒影为,则该车的牌照号码是_________.
例2(折叠问题)
如图:将一张矩形纸片ABCD的角C沿着GF折叠(F在BC边上,不与B、C重合)使得C点落在矩形ABCD内部的E处,FH平分∠BFE,则∠GFH的度数满足( ).
A. ; B. ;
C.; D.随着折痕位置变化而变化.
变式题组
1、如图,一张长方形纸沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于( )
A 108° B 114° C 126° D 129°
2.如图,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是( )
正三角形 B.正方形 C.正五边形 D.正六边形
3.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( )
A.六边形 B.八边形 C.十二边形 D.十六边形
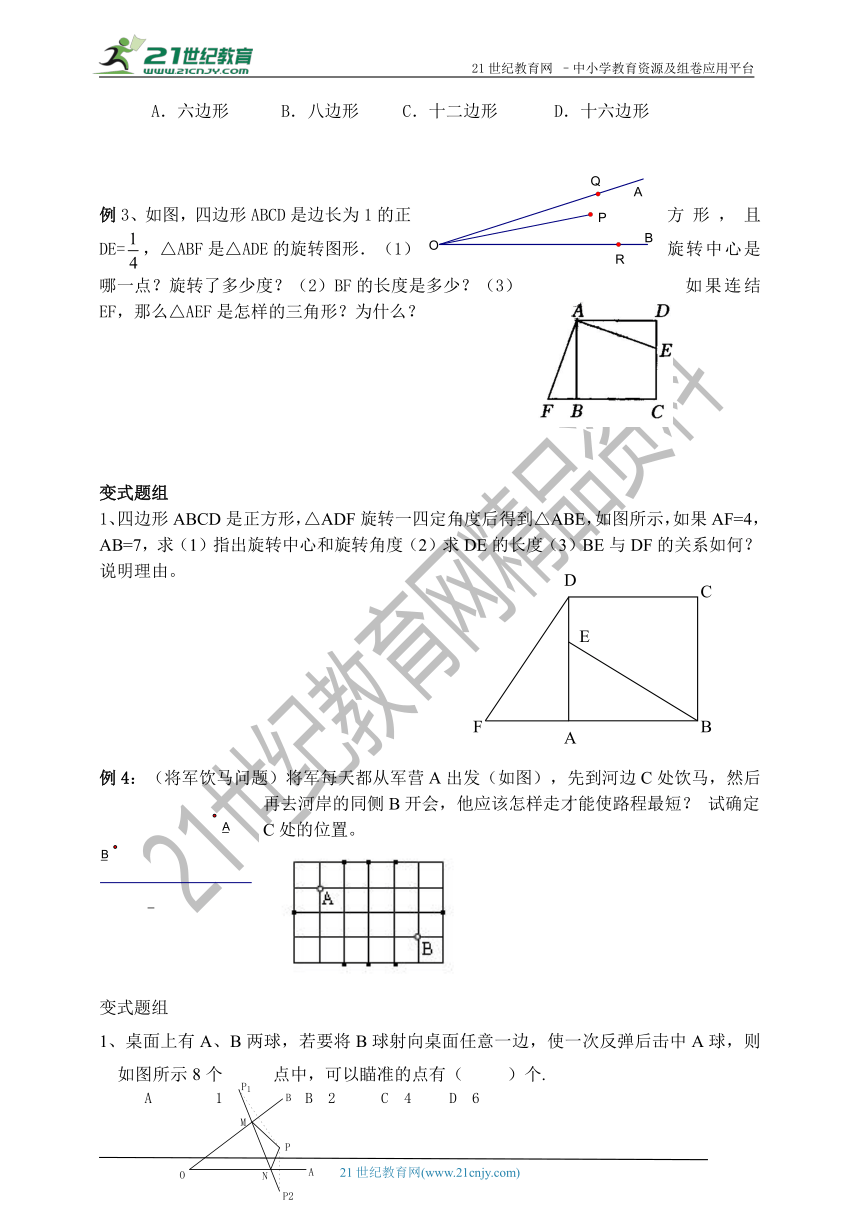
例3、如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.(1)旋转中心是哪一点?旋转了多少度?(2)BF的长度是多少?(3)如果连结EF,那么△AEF是怎样的三角形?为什么?
变式题组
1、四边形ABCD是正方形,△ADF旋转一四定角度后得到△ABE,如图所示,如果AF=4,AB=7,求(1)指出旋转中心和旋转角度(2)求DE的长度(3)BE与DF的关系如何?说明理由。
例4:(将军饮马问题)将军每天都从军营A出发(如图),先到河边C处饮马,然后再去河岸的同侧B开会,他应该怎样走才能使路程最短? 试确定C处的位置。
变式题组
1、桌面上有A、B两球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示8个点中,可以瞄准的点有( )个.
A 1 B 2 C 4 D 6
2、如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q、R(均不同于点O)则△PQR的周长的最小值是__。
3、已知:如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 .
4、如图9-98,△ABC中,点E在AC上,点N 在BC上,在AB上找一点F,使△ENF的周长最小。
5、(实际应用题)某班举行文艺晚会,桌子摆成两条直线(如图中的AO,BO),AO桌面上摆满了桔子,BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位,请你帮助他设计一条行走路线,使其所走的总路程最短?
6、如图,直线l1与直线l2互相垂直,A,B是两个定点.C,D分别是直线
l1,l2上的动点.试确定C,D两点的位置,使四边形ACDB的周长最短.
巩固提高
1.下列图形中既是轴对称图形,又是中心对称图形的是( )
2.如图2,将矩形纸片ABCD(图1)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸片收展平,那么∠AFE的度数为( ).
(A)60° (B)67.5° (C)72° (D)75°
拔高训练
1、如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
A、100 B、150 C、200 D、250
2、在旷野上,一个人骑马从A处出发,他先到河边N饮水,再到草场M处放马,然后返回A地,如图,请问他应该怎样走才能使总路程最短?
3、如图,从A地到B地经过一条小河(两岸平行),今要在河上建一座桥(桥与河岸垂直),应如何选择桥的位置才能使A到B的路程最短
如图,正方形ABCD中,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,当DQ+PQ取得最小值时,找出点P,点Q的位置.
第十一讲 轴对称、平移与旋转答案
一、知识网络
二、知识回顾,自主盘点
(一)轴对称与轴对称图形
1、定义:(1)如果一个图形沿某条 直线 对折,直线两旁的部分能 完全重合 ,这个图形叫做轴对称图形。
(2)把一个图形沿着某条直线翻折过去,如果它能够与 另一个图形完全重合 ,那么就说这两个图形成轴对称,这条直线就是 对称轴 。
2、特征:轴对称图形的对称轴,是任意一组对应点连线的 中垂线 。由轴对称变换得到的图形与原图 形状 、 大小 完全相同。
(二)图形的平移
1、定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,平移不改变图形的形状和大小.
两要素: 方向 和 距离 ;
2、特征①平移后的图形与原来图形的对应线段 平行且相等 ,或在同一直线上。
②对应角 相等,平移后对应点所连的线段平行且相等 ,或在同一直线上。
③平移不改变图形的形状和大小.
(三).图形旋转
1、定义:旋转是指图形绕着某一个固定点按一定方向(顺时针或逆时针)旋转一定的角度(小于360°),三要素: 旋转中心 、 旋转方向 和 旋转角度 ;
2、特征①图形上的每一个点都绕着旋转中心按同一旋转方向旋转了 相同大小的角度;
② 对应点到旋转中心的距离 相等 ,对应点与旋转中心所连线段的夹角就是旋转角 ③对应线段 相等 ,对应角 相等 ④旋转前后的图形 形状和大小不变。
(四).中心对称
(1)把一个图形绕着 一个固定点 旋转 180°后能与自身重合,那么这个图形叫做中心对称图形,这个点就是它的 对称中心 。
(2)把一个图形绕着某一点旋转 180° ,如果它能与另一个图形 完全重合 ,那么,我们就说这两个图形成中心对称。
注意:经过对称中心的直线将中心对称图形分为 面积 相等的两个部分。
旋转对称图形可以旋转任意的角度,而中心对称图形必须旋转180°.
(五)图形的全等
特征:全等图形的对应边相等,对应角相等
三、 基础夯实
1. 下列图形中,既是轴对称图形又是中心对称图形的是( A )
A. 菱形 B.梯形 C. 正三角形 D.正五边形
2、平移图形对应点的连线( D )
A 平行 B相等 C 平行且相等 D 平行且相等或在同一直线上 。
3、如图是正方体的展开图中,既不是轴对称图形,也不是中心对称图形的是(A )
4、如图所示,由△ABC平移得到的三角形的个数是( 9 )个;
5、下列图形中是轴对称图形的有( 6 )个
①角 ②线段 ③等腰三角形 ④等边三角形 ⑤扇形 ⑥圆⑦平行四边形
6、如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,则阴影部分面积为 168 .
7、如图,△OAB绕点O逆时针旋转600到△OCD的位置。已知∠AOB =350,则∠AOD=( D )A 450 B 200 C 400 D 250
8、如图,正方形网格中,△ABC的顶点及点O都在格点上.(略)
①画出△ABC关于点O中心对称的对称图形△A′B′C′;
②画出△ABC绕点O顺时针旋转90°的图形△A″B″C″.
③画出△ABC向下平移2格后的图形△A B C
9、请你画一条直线,把下图分成面积相等的两部分.
三、典型例题
例1、一只小狗正在平面镜前欣赏自己的全身像(如图所示),此时它所看到的全身像是(A )
变式题组
1、小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,
则电子表的实际时刻是10:21___,
2、小亮在镜中看到身后墙上的时钟如上,你认为实际时间最接近八点的是_D___
3、一个汽车车牌在水中的倒影为,则该车的牌照号码是_W5236499________.
例2(折叠问题)
如图:将一张矩形纸片ABCD的角C沿着GF折叠(F在BC边上,不与B、C重合)使得C点落在矩形ABCD内部的E处,FH平分∠BFE,则∠GFH的度数满足( B ).
A. ;B. ;
C.;D.随着折痕位置变化而变化.
变式题组
1、如图,一张长方形纸沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于( C )A 108° B 114° C 126° D 129°
2、如图,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是( D )
正三角形 B.正方形 C.正五边形 D.正六边形
3、把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( B )
A.六边形 B.八边形 C.十二边形 D.十六边形
例3、如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.(1)旋转中心是哪一点?旋转了多少度?(2)BF的长度是多少?(3)如果连结EF,那么△AEF是怎样的三角形?为什么?
解:(1)旋转中心是A点;旋转了90度
(2)∵△ABF是由△ADE旋转而成的
∴BF=DE
(3)∵∠EAF=90°(与旋转角相等)且AF=AE
∴△EAF是等腰直角三角形。
5、四边形ABCD是正方形,△ADF旋转一四定角度后得到△ABE,如图所示,如果AF=4,AB=7,求(1)指出旋转中心和旋转角度(2)求DE的长度(3)BE与DF的关系如何?说明理由。
解:(1)旋转中心:点A 旋转角度:90°;
(2)DE=3;
(3)∵∠EAF=90°,∠EBA=∠FDA,
∴延长BE与DF相交于点G,则∠GDE+∠DEG=90°,
∴BE⊥DF,即BE与DF是垂直关系。
例4:(将军饮马问题)将军每天都从军营A出发(如图),先到河边C处饮马,然后再去河岸的同侧B开会,他应该怎样走才能使路程最短? 试确定C处的位置(略)。
变式题组
1、桌面上有A、B两球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示8个点中,可以瞄准的点有( B )个.
A 1 B 2 C 4 D 6
2、如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q、R(均不同于点O)则△PQR的周长的最小值是10cm_。
3、已知:如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点
P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 15cm .
4、 如图9-98,△ABC中,点E在AC上,点N 在BC上,在AB上找一点F,
使△ENF的周长最小(答案略)。
5、(实际应用题)某班举行文艺晚会,桌子摆成两条直线(如图中的AO,BO),AO桌面上摆满了桔子,BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位,请你帮助他设计一条行走路线,使其所走的总路程最短?
作法參考:
(1)作点C关于OA ( https: / / www. / s wd=OA&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )的对称点A′,
(2)作点C关于OB ( https: / / www. / s wd=OB&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )的对称点B′,
(3)连接A′B′,分别于OA ( https: / / www. / s wd=OA&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )、OB ( https: / / www. / s wd=OB&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )相交于点D、点E,
(4)连接CD ( https: / / www. / s wd=CD&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )、CE ( https: / / www. / s wd=CE&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ),
则C→D→E→C就是小明 ( https: / / www. / s wd=%E5%B0%8F%E6%98%8E&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )所走的最短路线.
6、如图,直线l1与直线l2互相垂直,A,B是两个定点.C,D分别是直线
l1,l2上的动点.试确定C,D两点的位置,使四边形ACDB的周长最短.
作法參考:①画点A关于直线l2的对称点A′,点B关于直线l1的对称点B′.
②连结A′B′,A′B′分别交直线l1,l2于C′D′两点.
③连结AD′,BC′
巩固提高
1.下列图形中既是轴对称图形,又是中心对称图形的是( B )
2.如图2,将矩形纸片ABCD(图1)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸片收展平,那么∠AFE的度数为(B ).
(A)60° (B)67.5° (C)72° (D)75°
拔高
1、如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( B )
A、100 B、150 C、200 D、250
2、在旷野上,一个人骑马从A处出发,他先到河边N饮水,再到草场M处放马,然后返回A地,如图,请问他应该怎样走才能使总路程最短?
3、如图,从A地到B地经过一条小河(两岸平行),今要在河上建一座桥(桥与河岸垂直),应如何选择桥的位置才能使A到B的路程最短
4、如图,正方形ABCD中,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,当DQ+PQ取得最小值时,找出点P,点Q的位置.
3、作法參考:
①把A平移河宽的长度到A',且AA'⊥河岸,
②连结A'B交靠近B的河岸与C,
③作CD ( https: / / www. / s wd=CD&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )⊥另一河岸于D,
CD ( https: / / www. / s wd=CD&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )就是建桥的位置。
4、解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
图形的变换
平移
旋转
轴对称
轴对称
连结对应点的线段平行(或共线)且相等;
对应线段平行(或共线)且相等.
连结对应点的线段被 垂直平分
旋转对称
中心对称
变换后的图形与原来的图形位置改变,图形的形状和大小不变
第7题
B
A
C
D
E
F
_
_
B
_
A
图形的变换
平移
旋转
轴对称
轴对称
连结对应点的线段平行(或共线)且相等;
对应线段平行(或共线)且相等.
连结对应点的线段被 垂直平分
旋转对称
中心对称
变换后的图形与原来的图形位置改变,图形的形状和大小不变
第7题
B
A
C
D
E
F
_
_
B
_
A
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第十一讲 轴对称、平移与旋转
一、知识网络
二、知识回顾,自主盘点
(一)轴对称与轴对称图形
1、定义:(1)如果一个图形沿某条 对折,直线两旁的部分能 ,这个图形叫做轴对称图形。
(2)把一个图形沿着某条直线翻折过去,如果它能够与 ,那么就说这两个图形成轴对称,这条直线就是 。
2、特征:轴对称图形的对称轴,是任意一组对应点连线的 。由轴对称变换得到的图形与原图 、 完全相同。
(二)图形的平移
1、定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,平移不改变图形的形状和大小.
两要素: 和 ;
2、特征①:平移后的图形与原来图形的对应线段 且 ,或
②对应角 ;平移后对应点所连的线段 且或 。
③平移不改变图形的形状和大小.
(三)图形旋转
1、定义:旋转是指图形绕着某一个固定点按一定方向(顺时针或逆时针)旋转一定的角度(小于360°),三要素: 、 和 ;
2、特征①图形上的每一个点都绕着旋转中心按同一旋转方向旋转了 大小的角度;
② 对应点到旋转中心的距离 ,对应点与旋转中心所连线段的夹角就是 ③对应线段 ,对应角 ④旋转前后的图形 不变。
(四)中心对称
(1)把一个图形绕着 旋转 度后 能与自身重合,那么这个图形叫做中心对称图形,这个点就是它的 。
(2)把一个图形绕着某一点旋转 ,如果它能与另一个图形 ,那么,我们就说这两个图形成中心对称。
注意:经过对称中心的直线将中心对称图形分为 相同的两个部分。
旋转对称图形可以旋转任意的角度,而中心对称图形必须旋转180°.
(五)图形的全等特征:
三、基础夯实
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. 菱形 B.梯形 C. 正三角形 D.正五边形
2、平移图形对应点的连线( )
A 平行 B相等 C 平行且相等 D 平行且相等或在同一直线上 。
3、如图是正方体的展开图中,既不是轴对称图形,也不是中心对称图形的是( )
4、如图所示,由△ABC平移得到的三角形的个数是( )个;
5、下列图形中是轴对称图形的有( )个
①角 ②线段 ③等腰三角形 ④等边三角形 ⑤扇形 ⑥圆⑦平行四边形
6、如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,则阴影部分面积为 .
7、如图,△OAB绕点O逆时针旋转600到△OCD的位置。已知∠AOB =350,则∠AOD=( )A 450 B 200 C 400 D 250
8、如图,正方形网格中,△ABC的顶点及点O都在格点上.
①画出△ABC关于点O中心对称的对称图形△A′B′C′;
②画出△ABC绕点O顺时针旋转90°的图形△A″B″C″.
③画出△ABC向下平移2格后的图形△A B C
请你画一条直线,把下图分成面积相等的两部分.
三、典型例题
一只小狗正在平面镜前欣赏自己的全身像(如图所示),
此时它所看到的全身像是( )
变式题组
小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,
则电子表的实际时刻是___,
小亮在镜中看到身后墙上的时钟如上,你认为实际时间最接近八点的是____
一个汽车车牌在水中的倒影为,则该车的牌照号码是_________.
例2(折叠问题)
如图:将一张矩形纸片ABCD的角C沿着GF折叠(F在BC边上,不与B、C重合)使得C点落在矩形ABCD内部的E处,FH平分∠BFE,则∠GFH的度数满足( ).
A. ; B. ;
C.; D.随着折痕位置变化而变化.
变式题组
1、如图,一张长方形纸沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于( )
A 108° B 114° C 126° D 129°
2.如图,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是( )
正三角形 B.正方形 C.正五边形 D.正六边形
3.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( )
A.六边形 B.八边形 C.十二边形 D.十六边形
例3、如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.(1)旋转中心是哪一点?旋转了多少度?(2)BF的长度是多少?(3)如果连结EF,那么△AEF是怎样的三角形?为什么?
变式题组
1、四边形ABCD是正方形,△ADF旋转一四定角度后得到△ABE,如图所示,如果AF=4,AB=7,求(1)指出旋转中心和旋转角度(2)求DE的长度(3)BE与DF的关系如何?说明理由。
例4:(将军饮马问题)将军每天都从军营A出发(如图),先到河边C处饮马,然后再去河岸的同侧B开会,他应该怎样走才能使路程最短? 试确定C处的位置。
变式题组
1、桌面上有A、B两球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示8个点中,可以瞄准的点有( )个.
A 1 B 2 C 4 D 6
2、如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q、R(均不同于点O)则△PQR的周长的最小值是__。
3、已知:如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 .
4、如图9-98,△ABC中,点E在AC上,点N 在BC上,在AB上找一点F,使△ENF的周长最小。
5、(实际应用题)某班举行文艺晚会,桌子摆成两条直线(如图中的AO,BO),AO桌面上摆满了桔子,BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位,请你帮助他设计一条行走路线,使其所走的总路程最短?
6、如图,直线l1与直线l2互相垂直,A,B是两个定点.C,D分别是直线
l1,l2上的动点.试确定C,D两点的位置,使四边形ACDB的周长最短.
巩固提高
1.下列图形中既是轴对称图形,又是中心对称图形的是( )
2.如图2,将矩形纸片ABCD(图1)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸片收展平,那么∠AFE的度数为( ).
(A)60° (B)67.5° (C)72° (D)75°
拔高训练
1、如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
A、100 B、150 C、200 D、250
2、在旷野上,一个人骑马从A处出发,他先到河边N饮水,再到草场M处放马,然后返回A地,如图,请问他应该怎样走才能使总路程最短?
3、如图,从A地到B地经过一条小河(两岸平行),今要在河上建一座桥(桥与河岸垂直),应如何选择桥的位置才能使A到B的路程最短
如图,正方形ABCD中,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,当DQ+PQ取得最小值时,找出点P,点Q的位置.
第十一讲 轴对称、平移与旋转答案
一、知识网络
二、知识回顾,自主盘点
(一)轴对称与轴对称图形
1、定义:(1)如果一个图形沿某条 直线 对折,直线两旁的部分能 完全重合 ,这个图形叫做轴对称图形。
(2)把一个图形沿着某条直线翻折过去,如果它能够与 另一个图形完全重合 ,那么就说这两个图形成轴对称,这条直线就是 对称轴 。
2、特征:轴对称图形的对称轴,是任意一组对应点连线的 中垂线 。由轴对称变换得到的图形与原图 形状 、 大小 完全相同。
(二)图形的平移
1、定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,平移不改变图形的形状和大小.
两要素: 方向 和 距离 ;
2、特征①平移后的图形与原来图形的对应线段 平行且相等 ,或在同一直线上。
②对应角 相等,平移后对应点所连的线段平行且相等 ,或在同一直线上。
③平移不改变图形的形状和大小.
(三).图形旋转
1、定义:旋转是指图形绕着某一个固定点按一定方向(顺时针或逆时针)旋转一定的角度(小于360°),三要素: 旋转中心 、 旋转方向 和 旋转角度 ;
2、特征①图形上的每一个点都绕着旋转中心按同一旋转方向旋转了 相同大小的角度;
② 对应点到旋转中心的距离 相等 ,对应点与旋转中心所连线段的夹角就是旋转角 ③对应线段 相等 ,对应角 相等 ④旋转前后的图形 形状和大小不变。
(四).中心对称
(1)把一个图形绕着 一个固定点 旋转 180°后能与自身重合,那么这个图形叫做中心对称图形,这个点就是它的 对称中心 。
(2)把一个图形绕着某一点旋转 180° ,如果它能与另一个图形 完全重合 ,那么,我们就说这两个图形成中心对称。
注意:经过对称中心的直线将中心对称图形分为 面积 相等的两个部分。
旋转对称图形可以旋转任意的角度,而中心对称图形必须旋转180°.
(五)图形的全等
特征:全等图形的对应边相等,对应角相等
三、 基础夯实
1. 下列图形中,既是轴对称图形又是中心对称图形的是( A )
A. 菱形 B.梯形 C. 正三角形 D.正五边形
2、平移图形对应点的连线( D )
A 平行 B相等 C 平行且相等 D 平行且相等或在同一直线上 。
3、如图是正方体的展开图中,既不是轴对称图形,也不是中心对称图形的是(A )
4、如图所示,由△ABC平移得到的三角形的个数是( 9 )个;
5、下列图形中是轴对称图形的有( 6 )个
①角 ②线段 ③等腰三角形 ④等边三角形 ⑤扇形 ⑥圆⑦平行四边形
6、如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,则阴影部分面积为 168 .
7、如图,△OAB绕点O逆时针旋转600到△OCD的位置。已知∠AOB =350,则∠AOD=( D )A 450 B 200 C 400 D 250
8、如图,正方形网格中,△ABC的顶点及点O都在格点上.(略)
①画出△ABC关于点O中心对称的对称图形△A′B′C′;
②画出△ABC绕点O顺时针旋转90°的图形△A″B″C″.
③画出△ABC向下平移2格后的图形△A B C
9、请你画一条直线,把下图分成面积相等的两部分.
三、典型例题
例1、一只小狗正在平面镜前欣赏自己的全身像(如图所示),此时它所看到的全身像是(A )
变式题组
1、小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,
则电子表的实际时刻是10:21___,
2、小亮在镜中看到身后墙上的时钟如上,你认为实际时间最接近八点的是_D___
3、一个汽车车牌在水中的倒影为,则该车的牌照号码是_W5236499________.
例2(折叠问题)
如图:将一张矩形纸片ABCD的角C沿着GF折叠(F在BC边上,不与B、C重合)使得C点落在矩形ABCD内部的E处,FH平分∠BFE,则∠GFH的度数满足( B ).
A. ;B. ;
C.;D.随着折痕位置变化而变化.
变式题组
1、如图,一张长方形纸沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于( C )A 108° B 114° C 126° D 129°
2、如图,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是( D )
正三角形 B.正方形 C.正五边形 D.正六边形
3、把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( B )
A.六边形 B.八边形 C.十二边形 D.十六边形
例3、如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.(1)旋转中心是哪一点?旋转了多少度?(2)BF的长度是多少?(3)如果连结EF,那么△AEF是怎样的三角形?为什么?
解:(1)旋转中心是A点;旋转了90度
(2)∵△ABF是由△ADE旋转而成的
∴BF=DE
(3)∵∠EAF=90°(与旋转角相等)且AF=AE
∴△EAF是等腰直角三角形。
5、四边形ABCD是正方形,△ADF旋转一四定角度后得到△ABE,如图所示,如果AF=4,AB=7,求(1)指出旋转中心和旋转角度(2)求DE的长度(3)BE与DF的关系如何?说明理由。
解:(1)旋转中心:点A 旋转角度:90°;
(2)DE=3;
(3)∵∠EAF=90°,∠EBA=∠FDA,
∴延长BE与DF相交于点G,则∠GDE+∠DEG=90°,
∴BE⊥DF,即BE与DF是垂直关系。
例4:(将军饮马问题)将军每天都从军营A出发(如图),先到河边C处饮马,然后再去河岸的同侧B开会,他应该怎样走才能使路程最短? 试确定C处的位置(略)。
变式题组
1、桌面上有A、B两球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示8个点中,可以瞄准的点有( B )个.
A 1 B 2 C 4 D 6
2、如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q、R(均不同于点O)则△PQR的周长的最小值是10cm_。
3、已知:如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点
P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 15cm .
4、 如图9-98,△ABC中,点E在AC上,点N 在BC上,在AB上找一点F,
使△ENF的周长最小(答案略)。
5、(实际应用题)某班举行文艺晚会,桌子摆成两条直线(如图中的AO,BO),AO桌面上摆满了桔子,BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位,请你帮助他设计一条行走路线,使其所走的总路程最短?
作法參考:
(1)作点C关于OA ( https: / / www. / s wd=OA&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )的对称点A′,
(2)作点C关于OB ( https: / / www. / s wd=OB&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )的对称点B′,
(3)连接A′B′,分别于OA ( https: / / www. / s wd=OA&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )、OB ( https: / / www. / s wd=OB&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )相交于点D、点E,
(4)连接CD ( https: / / www. / s wd=CD&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )、CE ( https: / / www. / s wd=CE&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ),
则C→D→E→C就是小明 ( https: / / www. / s wd=%E5%B0%8F%E6%98%8E&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )所走的最短路线.
6、如图,直线l1与直线l2互相垂直,A,B是两个定点.C,D分别是直线
l1,l2上的动点.试确定C,D两点的位置,使四边形ACDB的周长最短.
作法參考:①画点A关于直线l2的对称点A′,点B关于直线l1的对称点B′.
②连结A′B′,A′B′分别交直线l1,l2于C′D′两点.
③连结AD′,BC′
巩固提高
1.下列图形中既是轴对称图形,又是中心对称图形的是( B )
2.如图2,将矩形纸片ABCD(图1)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸片收展平,那么∠AFE的度数为(B ).
(A)60° (B)67.5° (C)72° (D)75°
拔高
1、如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( B )
A、100 B、150 C、200 D、250
2、在旷野上,一个人骑马从A处出发,他先到河边N饮水,再到草场M处放马,然后返回A地,如图,请问他应该怎样走才能使总路程最短?
3、如图,从A地到B地经过一条小河(两岸平行),今要在河上建一座桥(桥与河岸垂直),应如何选择桥的位置才能使A到B的路程最短
4、如图,正方形ABCD中,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,当DQ+PQ取得最小值时,找出点P,点Q的位置.
3、作法參考:
①把A平移河宽的长度到A',且AA'⊥河岸,
②连结A'B交靠近B的河岸与C,
③作CD ( https: / / www. / s wd=CD&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )⊥另一河岸于D,
CD ( https: / / www. / s wd=CD&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )就是建桥的位置。
4、解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
图形的变换
平移
旋转
轴对称
轴对称
连结对应点的线段平行(或共线)且相等;
对应线段平行(或共线)且相等.
连结对应点的线段被 垂直平分
旋转对称
中心对称
变换后的图形与原来的图形位置改变,图形的形状和大小不变
第7题
B
A
C
D
E
F
_
_
B
_
A
图形的变换
平移
旋转
轴对称
轴对称
连结对应点的线段平行(或共线)且相等;
对应线段平行(或共线)且相等.
连结对应点的线段被 垂直平分
旋转对称
中心对称
变换后的图形与原来的图形位置改变,图形的形状和大小不变
第7题
B
A
C
D
E
F
_
_
B
_
A
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
