22.1.3 y=a(x-h)2+k的图象和性质同步作业
文档属性
| 名称 | 22.1.3 y=a(x-h)2+k的图象和性质同步作业 |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-23 10:04:21 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
22.1.3 y=a(x-h)2+k的图象和性质同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.抛物线y=2(x+3)2﹣4的顶点坐标是( )
A. (3,4) B. (3,﹣4) C. (﹣3,4) D. (﹣3,﹣4)
2.二次函数( )
A. 有最大值1 B. 有最小值1 C. 有最大值3 D. 有最小值3
3.对于二次函数y=-3(x-8)2+2,下列说法中,正确的是( )
A. 开口向上,顶点坐标为(8,2) B. 开口向下,顶点坐标为(8,2)
C. 开口向上,顶点坐标为(-8,2) D. 开口向下,顶点坐标为(-8,2)
4.已知二次函数y=3(x﹣2)2+5,则有( )
A. 当x>﹣2时,y随x的增大而减小 B. 当x>﹣2时,y随x的增大而增大
C. 当x>2时,y随x的增大而减小 D. 当x>2时,y随x的增大而增大
5.对于二次函数的图像,给出下列结论:①开口向上;②对称轴是直线;③顶
点坐标是;④与轴有两个交点.其中正确的结论是( )
A. ①② B. ③④ C. ②③ D. ①④
6.已知二次函数有最大值0,则a,b的大小关系为( )
A. < B. C. > D. 大小不能确定
7.在平面直角坐标系中,二次函数y=a(x–h)2+k(a<0)的图象可能是
A. B. C. D.
8.已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )
A. 3﹣或1+ B. 3﹣或3+ C. 3+或1﹣ D. 1﹣或1+
二、填空题
9.函数的最小值是__________.
10.已知点A(x1,y1)和B(x2,y2)是抛物线y=2(x﹣3)2+5上的两点,如果x1>x2>4,那么y1_____y2.(填“>”、“=”或“<”)
11.已知函数为常数),当<时,随的增大而减小,则的取值范为______.
12.若抛物线y=(x-m)+(m+1)的顶点在第一象限,则m的取值范围为________.
13.已知二次函数y=a(x﹣1)2﹣2(a≠0)的图象在﹣1<x<0这一段位于x轴下方,在3<x<4这一段位于x轴的上方,则a的值为 .
14.把抛物线y=﹣x2先向上平移2个单位,再向左平移3个单位,所得的抛物线是_____.
15.如图,抛物线y1=a(x+2)2﹣3与y2=(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4
④2AB=3AC.
其中正确结论是______.
三、解答题
16.已知二次函数的图象的顶点坐标为(﹣2,﹣3),且图象过点(﹣3,﹣1),求这个二次函数的解析式.
17.把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y= (x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标.
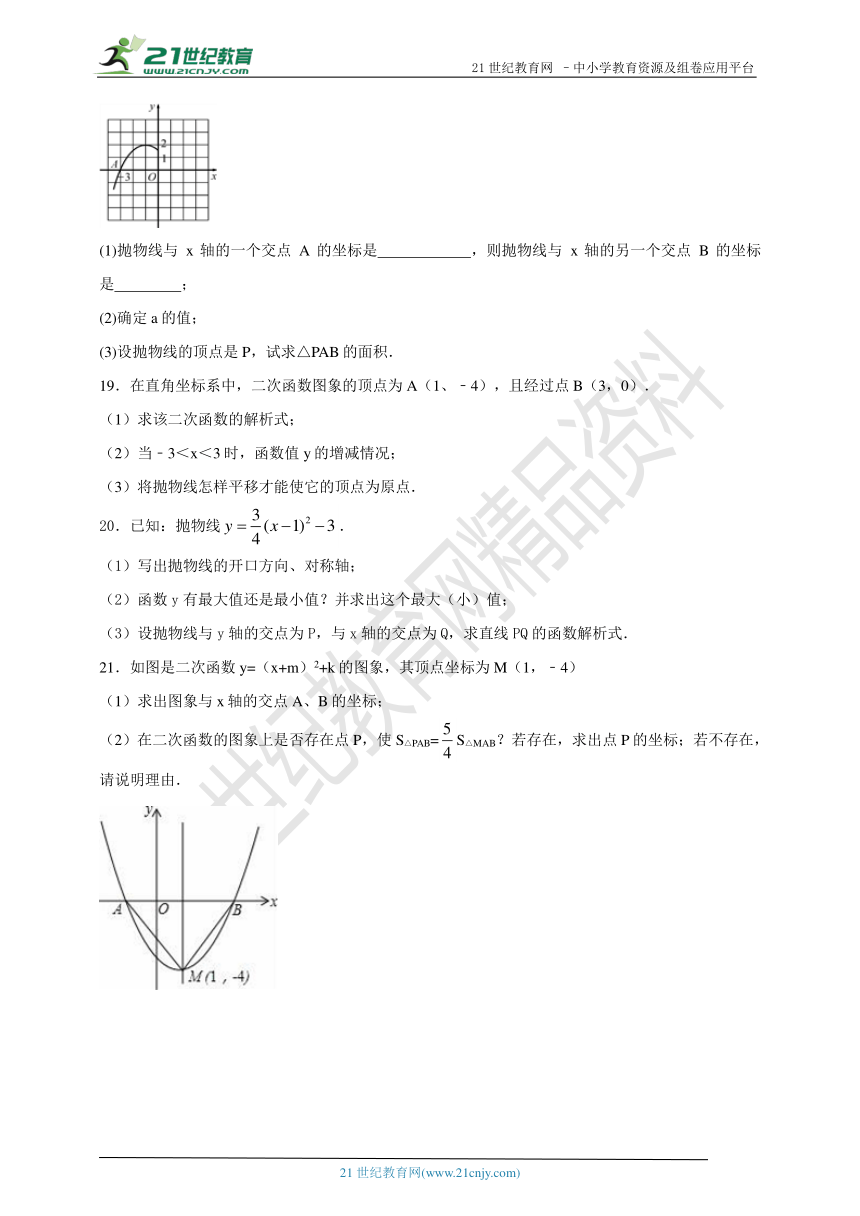
18.如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题:
(1)抛物线与x轴的一个交点A的坐标是 ,则抛物线与x轴的另一个交点B的坐标是 ;
(2)确定a的值;
(3)设抛物线的顶点是P,试求△PAB的面积.
19.在直角坐标系中,二次函数图象的顶点为A(1、﹣4),且经过点B(3,0).
(1)求该二次函数的解析式;
(2)当﹣3<x<3时,函数值y的增减情况;
(3)将抛物线怎样平移才能使它的顶点为原点.
20.已知:抛物线.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
21.如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,﹣4)
(1)求出图象与x轴的交点A、B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
1.D
【解析】∵y=2(x+3)2﹣4,
∴抛物线顶点坐标为(﹣3,﹣4),
故选:D.
2.D
【解析】解:∵a=1>0,∴二次函数有最小值3.故选D.
3.B
【解析】∵-3<0,
∴开口向下.
∵解析式是:y=-3(x-8)2+2,
∴顶点坐标为(8,2).
故选B.
点睛:本题考查了二次函数y=a(x-h)2+k的性质,当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;其顶点坐标是(h,k).
4.D
【解析】试题解析:∵
∴抛物线开口向上,对称轴为x=2,顶点坐标为(2,5),
∴A、B、C都不正确,
∵二次函数的图象为一条抛物线,当时,y随x的增大而增大
∴D正确,
故选D.
5.D
【解析】分析:根据二次函数的顶点式,可知对称轴为x=h,顶点为(h,k),然后由系数a和k判断开口方向和与x轴的交点.
详解:∵a=1>0
∴开口向上,①正确;
∵x-3=0
∴对称轴为x=3,②错误;
∴顶点坐标为:(3,-4),故③错误;
∴在第四象限,
所以与x轴有两个交点.故④正确.
故选:D.
点睛:此题主要考查了二次函数的顶点式以及顶点式中系数与图像的关系,关键是明确顶点式中的系数a、h、k的值及符号,注意结合图像判断.
6.A
【解析】【分析】根据二次函数有最大值可判断a<0,再根据最大值为0可判断b=0,据此即可进行比较a、b的大小.
【详解】∵二次函数y=a(x+1)2-b(a≠0)有最大值,
∴抛物线开口方向向下,即a<0,
又最大值为0,∴b=0,
∴a故选A.
【点睛】本题考查了二次函数的顶点式以及二次函数的性质,熟练掌握二次函数的性质是解题的关键.
7.B
【解析】二次函数y=a(x–h)2+k(a<0)的顶点坐标为(h,k),它的开口方向向下,故选B.
8.C
【解析】∵当x<h时,y随x的增大而增大,当x>h时,y随x的增大而减小,
∴①若h<1≤x≤3,x=1时,y取得最小值-5,
可得:-(1-h)2+1=-5,
解得:h=1-或h=1+(舍);
②若1≤x≤3<h,当x=3时,y取得最小值-5,
可得:-(3-h)2+1=-5,
解得:h=3+或h=3-(舍).
综上,h的值为1-或3+,
故选:C.
点睛:本题主要考查二次函数的性质和最值,根据二次函数的增减性和最值分两种情况讨论是解题的关键.
9.-2
【解析】分析:由二次项系数的正负,根据二次函数的性质即可得出其最值情况.
详解:在函数y=中,∵a=>0,∴当x=﹣1时,y取得最小值﹣2.
故答案为:﹣2.
点睛:本题主要考查二次函数的最值,解题的关键是熟练掌握二次函数的图象和性质.
10.>
【解析】∵y=2(x﹣3)2+5,
∴a=2>0,有最小值为5,
∴抛物线开口向上,
∵抛物线y=2(x﹣3)2+5对称轴为直线x=3,
∵x1>x2>4,
∴y1>y2.
故答案为:>
点睛:本题考察了二次函数的图像和性质,当a>0时,在对称轴的左侧y随x的增大而减小,在对称轴的右侧y随x的增大而增大;当a<0时,在对称轴的左侧y随x的增大而增大,在对称轴的右侧y随x的增大而减小.
11.m≤3
【解析】分析: 根据y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,可得答案.
详解: ,
∵a=2>0,对称轴x=3
∴当x≤3时,y随x的增大而减小.
∴m≤3.
故答案为:x≤3.
点睛: 本题考查了二次函数的性质,二次函数y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.
12.m>0
【解析】解:∵抛物线y=(x﹣m)2+(m+1),∴顶点坐标为(m,m+1).∵顶点在第一象限,∴m>0,m+1>0,∴m的取值范围为m>0.故答案为:m>0.
13..
【解析】试题分析:∵抛物线y=a(x﹣1)2﹣2(a≠0)的对称轴为直线x=1,
而抛物线在3<x<4这一段位于x轴的上方,
∴抛物线在﹣2<x<﹣1这一段位于x轴的上方,
∵抛物线在﹣1<x<0这一段位于x轴的下方,
∴抛物线过点(﹣1,0),
把(﹣1,0)代入y=a(x﹣1)2﹣2(a≠0)得4a﹣2=0,解得a=.
故答案为.
点睛:本题主要考查了二次函数的性质,根据二次函数的对称性得出图象经过点(-1,0)是解决此题的关键.
14.y=﹣(x+3)2+2
【解析】
试题分析:根据二次函数的平移的规律:上加下减,左加右减,直接可得y=-x 平移后的图像为:y=-(x+3) +2.
点睛:此题主要考查了二次函数的平移规律,根据“左加右减,上加下减”,分别对函数的横纵坐标进行变化,直接代入即可求解,解题时一定要注意平移的方向,以及关系式中的符号变化.
15.①④
【解析】(1)∵抛物线y2=(x﹣3)2+1的开口向上,顶点在x轴上方,
∴y2的值总是正数.故①正确;
(2)把点A(1,3)代入y1=a(x+2)2﹣3得:3=a(1+2)2-3,解得:a=,
∴②错误;
(3)∵当时, , ,
∴.
∴③错误;
(4)∵在中,当时,可得,解得: ,∴点B的坐标为(-5,3);
∵在中,当时,可得,解得: ,
∴点C的坐标为(5,3);
∴AB=6,AC=4,
∴2AB=3AC.
∴④正确;
综上所述:正确的是①④.
16.y=2(x+2)2﹣3
【解析】【试题分析】已知顶点坐标,设成顶点式y=a(x+2)2﹣3,将(﹣3,﹣1)代入即可.
【试题解析】
设解析式为:y=a(x+2)2﹣3,
将(﹣3,﹣1)代入得出:﹣1=a(﹣3+2)2﹣3,
解得: a=2.
故这个二次函数的解析式为:y=2(x+2)2﹣3
【方法点睛】本题目是一道求解二次函数的解析式问题,已知顶点就设为顶点式简便.
17.(1)a=,h=1,k=-5;(2)开口向上,对称轴为x=1,顶点坐标为(1,-5).
【解析】试题分析:(1)二次函数的平移,可以看作是将二次函数y= (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k,然后再按二次函数图象的平移法则,确定函数解析式,即可得到结论;
(2),直接根据函数解析式,结合二次函数的性质,进行回答即可.
试题分析:(1)∵二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y= (x+1)2-1,
∴可以看作是将二次函数y= (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k,
而将二次函数y= (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数为:y= (x-1)2-5,
∴a=,b=1,k=-5;
(2)二次函数y= (x-1)2-5,
开口向上,对称轴为x=1,顶点坐标为(1,-5).
18.(1)(-3,0),(1,0) ;(2) a=- ;(3)4.
【解析】试题分析:(1)由图象可求得A点的坐标,由解析式可求得抛物线的对称轴方程,利用图象的对称性可求得B点坐标;
(2)把B点坐标代入抛物线解析式可求得a的值;
(3)由抛物线解析式可求得P点坐标,再结合A、B坐标可求得AB的值,则可求得△PAB的面积.
试题解析:(1)由图象可知A点坐标为( 3,0),
∵y=a(x+1)2+2,
∴抛物线对称轴方程为x= 1,
∵A、B两点关于对称轴对称,
∴B的坐标为(1,0),
故答案为:( 3,0);(1,0);
(2)将(1,0)代入y=a(x+1)2+2,
可得0=4a+2,解得a=- ;
(3)∵y=a(x+1)2+2,
∴抛物线的顶点坐标是(-1,2),
∵A(-3,0),B(1,0),
∴AB=1-(-3)=4,
∴S△PAB=×4×2=4.
19.(1)y=(x﹣1)2﹣4;(2)当﹣3<x<1时,y随x的增大而减小,当1≤x<3,y随x的增大而增大;(3)将抛物线y=(x﹣1)2﹣4向左平移1个单位,再向上平移4个单位即可实现抛物线顶点为原点.
【解析】试题分析:
(1)由已知条件可设二次函数的解析式为: ,再代入点(3,0)解出a的值即可得到二次函数的解析式;
(2)由(1)中所求解析式可得第(2)问答案;
(3)根据(1)中所得解析式可确定原来顶点的位置,这样就可确定怎样平移可将顶点移到原点了.
试题解析:
(1)∵二次函数图象的顶点为A(1,﹣4),
∴可设二次函数的解析式为y=a(x﹣1)2﹣4,
又∵二次函数图象过点B(3,0)
∴a(3﹣1)2﹣4=0,解得:a=1,
∴y=(x﹣1)2﹣4
(2)∵抛物线对称轴为直线x=1,且开口向上,
∴当﹣3<x<1时,y随x的增大而减小;当1≤x<3,y随x的增大而增大,
(3)将抛物线y=(x﹣1)2﹣4向左平移1个单位,再向上平移4个单位即可实现抛物线顶点为原点.
点睛:(1)当已知抛物线的顶点坐标,求解析式时,一般把解析式设为顶点式: 的形式;(2)本题中顶点的横坐标x=1在﹣3<x<3内,因此要分为:①﹣3<x<1和②1≤x<3两段来讨论函数值y的增减情况;(3)将抛物线进行平移时,“h”的值是“左移加,右移减”;“k”的值是“上移加,下移减”.
20.解:(1)抛物线,
∵a= >0,
∴抛物线的开口向上,
对称轴为x=1;
(2)∵a=>0,
∴函数y有最小值,最小值为-3;
(3)令x=0,则 ,
所以,点P的坐标为(0, ),
令y=0,则,
解得x1=-1,x2=3,
所以,点Q的坐标为(-1,0)或(3,0),
当点P(0, ),Q(-1,0)时,设直线PQ的解析式为y=kx+b,
则 ,解得 k=, b= ,
所以直线PQ的解析式为 ,
当P(0, ),Q(3,0)时,设直线PQ的解析式为y=mx+n,
则 ,解得 m= , n=- ,
所以,直线PQ的解析式为,
综上所述,直线PQ的解析式为或.
【解析】(1)根据二次函数的性质,写出开口方向与对称轴即可;
(2)根据a是正数确定有最小值,再根据函数解析式写出最小值;
(3)分别求出点P、Q的坐标,再根据待定系数法求函数解析式解答.
21.(1)A(﹣1,0),B(3,0);(2)存在合适的点P,坐标为(4,5)或(﹣2,5).
【解析】试题分析:
(1)由二次函数y=(x+m)2+k的顶点坐标为M(1,﹣4)可得解析式为: ,解方程: 可得点A、B的坐标;
(2)设点P的纵坐标为,由△PAB与△MAB同底,且S△PAB=S△MAB,可得: ,从而可得=,结合点P在抛物线的图象上,可得=5,由此得到: ,解方程即可得到点P的坐标.
试题解析:
(1)∵抛物线解析式为y=(x+m)2+k的顶点为M(1,﹣4)
∴,
当y=0时,(x﹣1)2﹣4=0,解得x1=3,x2=﹣1,
∴A(﹣1,0),B(3,0);
(2)∵△PAB与△MAB同底,且S△PAB=S△MAB,
∴,即=,
又∵点P在y=(x﹣1)2﹣4的图象上,
∴yP≥﹣4,
∴=5,则,解得: ,
∴存在合适的点P,坐标为(4,5)或(﹣2,5).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
22.1.3 y=a(x-h)2+k的图象和性质同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.抛物线y=2(x+3)2﹣4的顶点坐标是( )
A. (3,4) B. (3,﹣4) C. (﹣3,4) D. (﹣3,﹣4)
2.二次函数( )
A. 有最大值1 B. 有最小值1 C. 有最大值3 D. 有最小值3
3.对于二次函数y=-3(x-8)2+2,下列说法中,正确的是( )
A. 开口向上,顶点坐标为(8,2) B. 开口向下,顶点坐标为(8,2)
C. 开口向上,顶点坐标为(-8,2) D. 开口向下,顶点坐标为(-8,2)
4.已知二次函数y=3(x﹣2)2+5,则有( )
A. 当x>﹣2时,y随x的增大而减小 B. 当x>﹣2时,y随x的增大而增大
C. 当x>2时,y随x的增大而减小 D. 当x>2时,y随x的增大而增大
5.对于二次函数的图像,给出下列结论:①开口向上;②对称轴是直线;③顶
点坐标是;④与轴有两个交点.其中正确的结论是( )
A. ①② B. ③④ C. ②③ D. ①④
6.已知二次函数有最大值0,则a,b的大小关系为( )
A. < B. C. > D. 大小不能确定
7.在平面直角坐标系中,二次函数y=a(x–h)2+k(a<0)的图象可能是
A. B. C. D.
8.已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )
A. 3﹣或1+ B. 3﹣或3+ C. 3+或1﹣ D. 1﹣或1+
二、填空题
9.函数的最小值是__________.
10.已知点A(x1,y1)和B(x2,y2)是抛物线y=2(x﹣3)2+5上的两点,如果x1>x2>4,那么y1_____y2.(填“>”、“=”或“<”)
11.已知函数为常数),当<时,随的增大而减小,则的取值范为______.
12.若抛物线y=(x-m)+(m+1)的顶点在第一象限,则m的取值范围为________.
13.已知二次函数y=a(x﹣1)2﹣2(a≠0)的图象在﹣1<x<0这一段位于x轴下方,在3<x<4这一段位于x轴的上方,则a的值为 .
14.把抛物线y=﹣x2先向上平移2个单位,再向左平移3个单位,所得的抛物线是_____.
15.如图,抛物线y1=a(x+2)2﹣3与y2=(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4
④2AB=3AC.
其中正确结论是______.
三、解答题
16.已知二次函数的图象的顶点坐标为(﹣2,﹣3),且图象过点(﹣3,﹣1),求这个二次函数的解析式.
17.把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y= (x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标.
18.如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题:
(1)抛物线与x轴的一个交点A的坐标是 ,则抛物线与x轴的另一个交点B的坐标是 ;
(2)确定a的值;
(3)设抛物线的顶点是P,试求△PAB的面积.
19.在直角坐标系中,二次函数图象的顶点为A(1、﹣4),且经过点B(3,0).
(1)求该二次函数的解析式;
(2)当﹣3<x<3时,函数值y的增减情况;
(3)将抛物线怎样平移才能使它的顶点为原点.
20.已知:抛物线.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
21.如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,﹣4)
(1)求出图象与x轴的交点A、B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
1.D
【解析】∵y=2(x+3)2﹣4,
∴抛物线顶点坐标为(﹣3,﹣4),
故选:D.
2.D
【解析】解:∵a=1>0,∴二次函数有最小值3.故选D.
3.B
【解析】∵-3<0,
∴开口向下.
∵解析式是:y=-3(x-8)2+2,
∴顶点坐标为(8,2).
故选B.
点睛:本题考查了二次函数y=a(x-h)2+k的性质,当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;其顶点坐标是(h,k).
4.D
【解析】试题解析:∵
∴抛物线开口向上,对称轴为x=2,顶点坐标为(2,5),
∴A、B、C都不正确,
∵二次函数的图象为一条抛物线,当时,y随x的增大而增大
∴D正确,
故选D.
5.D
【解析】分析:根据二次函数的顶点式,可知对称轴为x=h,顶点为(h,k),然后由系数a和k判断开口方向和与x轴的交点.
详解:∵a=1>0
∴开口向上,①正确;
∵x-3=0
∴对称轴为x=3,②错误;
∴顶点坐标为:(3,-4),故③错误;
∴在第四象限,
所以与x轴有两个交点.故④正确.
故选:D.
点睛:此题主要考查了二次函数的顶点式以及顶点式中系数与图像的关系,关键是明确顶点式中的系数a、h、k的值及符号,注意结合图像判断.
6.A
【解析】【分析】根据二次函数有最大值可判断a<0,再根据最大值为0可判断b=0,据此即可进行比较a、b的大小.
【详解】∵二次函数y=a(x+1)2-b(a≠0)有最大值,
∴抛物线开口方向向下,即a<0,
又最大值为0,∴b=0,
∴a
【点睛】本题考查了二次函数的顶点式以及二次函数的性质,熟练掌握二次函数的性质是解题的关键.
7.B
【解析】二次函数y=a(x–h)2+k(a<0)的顶点坐标为(h,k),它的开口方向向下,故选B.
8.C
【解析】∵当x<h时,y随x的增大而增大,当x>h时,y随x的增大而减小,
∴①若h<1≤x≤3,x=1时,y取得最小值-5,
可得:-(1-h)2+1=-5,
解得:h=1-或h=1+(舍);
②若1≤x≤3<h,当x=3时,y取得最小值-5,
可得:-(3-h)2+1=-5,
解得:h=3+或h=3-(舍).
综上,h的值为1-或3+,
故选:C.
点睛:本题主要考查二次函数的性质和最值,根据二次函数的增减性和最值分两种情况讨论是解题的关键.
9.-2
【解析】分析:由二次项系数的正负,根据二次函数的性质即可得出其最值情况.
详解:在函数y=中,∵a=>0,∴当x=﹣1时,y取得最小值﹣2.
故答案为:﹣2.
点睛:本题主要考查二次函数的最值,解题的关键是熟练掌握二次函数的图象和性质.
10.>
【解析】∵y=2(x﹣3)2+5,
∴a=2>0,有最小值为5,
∴抛物线开口向上,
∵抛物线y=2(x﹣3)2+5对称轴为直线x=3,
∵x1>x2>4,
∴y1>y2.
故答案为:>
点睛:本题考察了二次函数的图像和性质,当a>0时,在对称轴的左侧y随x的增大而减小,在对称轴的右侧y随x的增大而增大;当a<0时,在对称轴的左侧y随x的增大而增大,在对称轴的右侧y随x的增大而减小.
11.m≤3
【解析】分析: 根据y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,可得答案.
详解: ,
∵a=2>0,对称轴x=3
∴当x≤3时,y随x的增大而减小.
∴m≤3.
故答案为:x≤3.
点睛: 本题考查了二次函数的性质,二次函数y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.
12.m>0
【解析】解:∵抛物线y=(x﹣m)2+(m+1),∴顶点坐标为(m,m+1).∵顶点在第一象限,∴m>0,m+1>0,∴m的取值范围为m>0.故答案为:m>0.
13..
【解析】试题分析:∵抛物线y=a(x﹣1)2﹣2(a≠0)的对称轴为直线x=1,
而抛物线在3<x<4这一段位于x轴的上方,
∴抛物线在﹣2<x<﹣1这一段位于x轴的上方,
∵抛物线在﹣1<x<0这一段位于x轴的下方,
∴抛物线过点(﹣1,0),
把(﹣1,0)代入y=a(x﹣1)2﹣2(a≠0)得4a﹣2=0,解得a=.
故答案为.
点睛:本题主要考查了二次函数的性质,根据二次函数的对称性得出图象经过点(-1,0)是解决此题的关键.
14.y=﹣(x+3)2+2
【解析】
试题分析:根据二次函数的平移的规律:上加下减,左加右减,直接可得y=-x 平移后的图像为:y=-(x+3) +2.
点睛:此题主要考查了二次函数的平移规律,根据“左加右减,上加下减”,分别对函数的横纵坐标进行变化,直接代入即可求解,解题时一定要注意平移的方向,以及关系式中的符号变化.
15.①④
【解析】(1)∵抛物线y2=(x﹣3)2+1的开口向上,顶点在x轴上方,
∴y2的值总是正数.故①正确;
(2)把点A(1,3)代入y1=a(x+2)2﹣3得:3=a(1+2)2-3,解得:a=,
∴②错误;
(3)∵当时, , ,
∴.
∴③错误;
(4)∵在中,当时,可得,解得: ,∴点B的坐标为(-5,3);
∵在中,当时,可得,解得: ,
∴点C的坐标为(5,3);
∴AB=6,AC=4,
∴2AB=3AC.
∴④正确;
综上所述:正确的是①④.
16.y=2(x+2)2﹣3
【解析】【试题分析】已知顶点坐标,设成顶点式y=a(x+2)2﹣3,将(﹣3,﹣1)代入即可.
【试题解析】
设解析式为:y=a(x+2)2﹣3,
将(﹣3,﹣1)代入得出:﹣1=a(﹣3+2)2﹣3,
解得: a=2.
故这个二次函数的解析式为:y=2(x+2)2﹣3
【方法点睛】本题目是一道求解二次函数的解析式问题,已知顶点就设为顶点式简便.
17.(1)a=,h=1,k=-5;(2)开口向上,对称轴为x=1,顶点坐标为(1,-5).
【解析】试题分析:(1)二次函数的平移,可以看作是将二次函数y= (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k,然后再按二次函数图象的平移法则,确定函数解析式,即可得到结论;
(2),直接根据函数解析式,结合二次函数的性质,进行回答即可.
试题分析:(1)∵二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y= (x+1)2-1,
∴可以看作是将二次函数y= (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k,
而将二次函数y= (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数为:y= (x-1)2-5,
∴a=,b=1,k=-5;
(2)二次函数y= (x-1)2-5,
开口向上,对称轴为x=1,顶点坐标为(1,-5).
18.(1)(-3,0),(1,0) ;(2) a=- ;(3)4.
【解析】试题分析:(1)由图象可求得A点的坐标,由解析式可求得抛物线的对称轴方程,利用图象的对称性可求得B点坐标;
(2)把B点坐标代入抛物线解析式可求得a的值;
(3)由抛物线解析式可求得P点坐标,再结合A、B坐标可求得AB的值,则可求得△PAB的面积.
试题解析:(1)由图象可知A点坐标为( 3,0),
∵y=a(x+1)2+2,
∴抛物线对称轴方程为x= 1,
∵A、B两点关于对称轴对称,
∴B的坐标为(1,0),
故答案为:( 3,0);(1,0);
(2)将(1,0)代入y=a(x+1)2+2,
可得0=4a+2,解得a=- ;
(3)∵y=a(x+1)2+2,
∴抛物线的顶点坐标是(-1,2),
∵A(-3,0),B(1,0),
∴AB=1-(-3)=4,
∴S△PAB=×4×2=4.
19.(1)y=(x﹣1)2﹣4;(2)当﹣3<x<1时,y随x的增大而减小,当1≤x<3,y随x的增大而增大;(3)将抛物线y=(x﹣1)2﹣4向左平移1个单位,再向上平移4个单位即可实现抛物线顶点为原点.
【解析】试题分析:
(1)由已知条件可设二次函数的解析式为: ,再代入点(3,0)解出a的值即可得到二次函数的解析式;
(2)由(1)中所求解析式可得第(2)问答案;
(3)根据(1)中所得解析式可确定原来顶点的位置,这样就可确定怎样平移可将顶点移到原点了.
试题解析:
(1)∵二次函数图象的顶点为A(1,﹣4),
∴可设二次函数的解析式为y=a(x﹣1)2﹣4,
又∵二次函数图象过点B(3,0)
∴a(3﹣1)2﹣4=0,解得:a=1,
∴y=(x﹣1)2﹣4
(2)∵抛物线对称轴为直线x=1,且开口向上,
∴当﹣3<x<1时,y随x的增大而减小;当1≤x<3,y随x的增大而增大,
(3)将抛物线y=(x﹣1)2﹣4向左平移1个单位,再向上平移4个单位即可实现抛物线顶点为原点.
点睛:(1)当已知抛物线的顶点坐标,求解析式时,一般把解析式设为顶点式: 的形式;(2)本题中顶点的横坐标x=1在﹣3<x<3内,因此要分为:①﹣3<x<1和②1≤x<3两段来讨论函数值y的增减情况;(3)将抛物线进行平移时,“h”的值是“左移加,右移减”;“k”的值是“上移加,下移减”.
20.解:(1)抛物线,
∵a= >0,
∴抛物线的开口向上,
对称轴为x=1;
(2)∵a=>0,
∴函数y有最小值,最小值为-3;
(3)令x=0,则 ,
所以,点P的坐标为(0, ),
令y=0,则,
解得x1=-1,x2=3,
所以,点Q的坐标为(-1,0)或(3,0),
当点P(0, ),Q(-1,0)时,设直线PQ的解析式为y=kx+b,
则 ,解得 k=, b= ,
所以直线PQ的解析式为 ,
当P(0, ),Q(3,0)时,设直线PQ的解析式为y=mx+n,
则 ,解得 m= , n=- ,
所以,直线PQ的解析式为,
综上所述,直线PQ的解析式为或.
【解析】(1)根据二次函数的性质,写出开口方向与对称轴即可;
(2)根据a是正数确定有最小值,再根据函数解析式写出最小值;
(3)分别求出点P、Q的坐标,再根据待定系数法求函数解析式解答.
21.(1)A(﹣1,0),B(3,0);(2)存在合适的点P,坐标为(4,5)或(﹣2,5).
【解析】试题分析:
(1)由二次函数y=(x+m)2+k的顶点坐标为M(1,﹣4)可得解析式为: ,解方程: 可得点A、B的坐标;
(2)设点P的纵坐标为,由△PAB与△MAB同底,且S△PAB=S△MAB,可得: ,从而可得=,结合点P在抛物线的图象上,可得=5,由此得到: ,解方程即可得到点P的坐标.
试题解析:
(1)∵抛物线解析式为y=(x+m)2+k的顶点为M(1,﹣4)
∴,
当y=0时,(x﹣1)2﹣4=0,解得x1=3,x2=﹣1,
∴A(﹣1,0),B(3,0);
(2)∵△PAB与△MAB同底,且S△PAB=S△MAB,
∴,即=,
又∵点P在y=(x﹣1)2﹣4的图象上,
∴yP≥﹣4,
∴=5,则,解得: ,
∴存在合适的点P,坐标为(4,5)或(﹣2,5).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
