第12章 一次函数 单元检测试题(含答案)
文档属性
| 名称 | 第12章 一次函数 单元检测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 103.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-22 08:11:09 | ||
图片预览




文档简介
第十二章达标测试卷
一、选择题(每题3分,共30分)
1.下列图象中,表示y不是x的函数的是( )
2.函数y=中自变量x的取值范围为( )
A.x≥0 B.x≥- C.x≥ D.x≤-
3.点(x1,y1),(x2,y2)在直线y=-x+b上,若x1<x2,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.无法确定
4.将函数y=-3x的图象沿y轴向上平移2个单位后,所得图象对应的函数表达式为( )
A.y=-3x+2 B.y=-3x-2
C.y=-3(x+2) D.y=-3(x-2)
5.直线y=x-1的图象经过的象限是( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
6.下列四个点中,有三个点在同一条直线上,不在这条直线上的点是( )
A.(-3,-1) B.(1,1) C.(3,2) D.(4,3)
7.如图所示,函数y1=|x|和y2=x+的图象相交于(-1,1),(2,2)两点.当y1>y2时,x的取值范围是( )
A.x<-1 B.-1<x<2
C.x>2 D.x<-1或x>2
(第7题) (第8题)
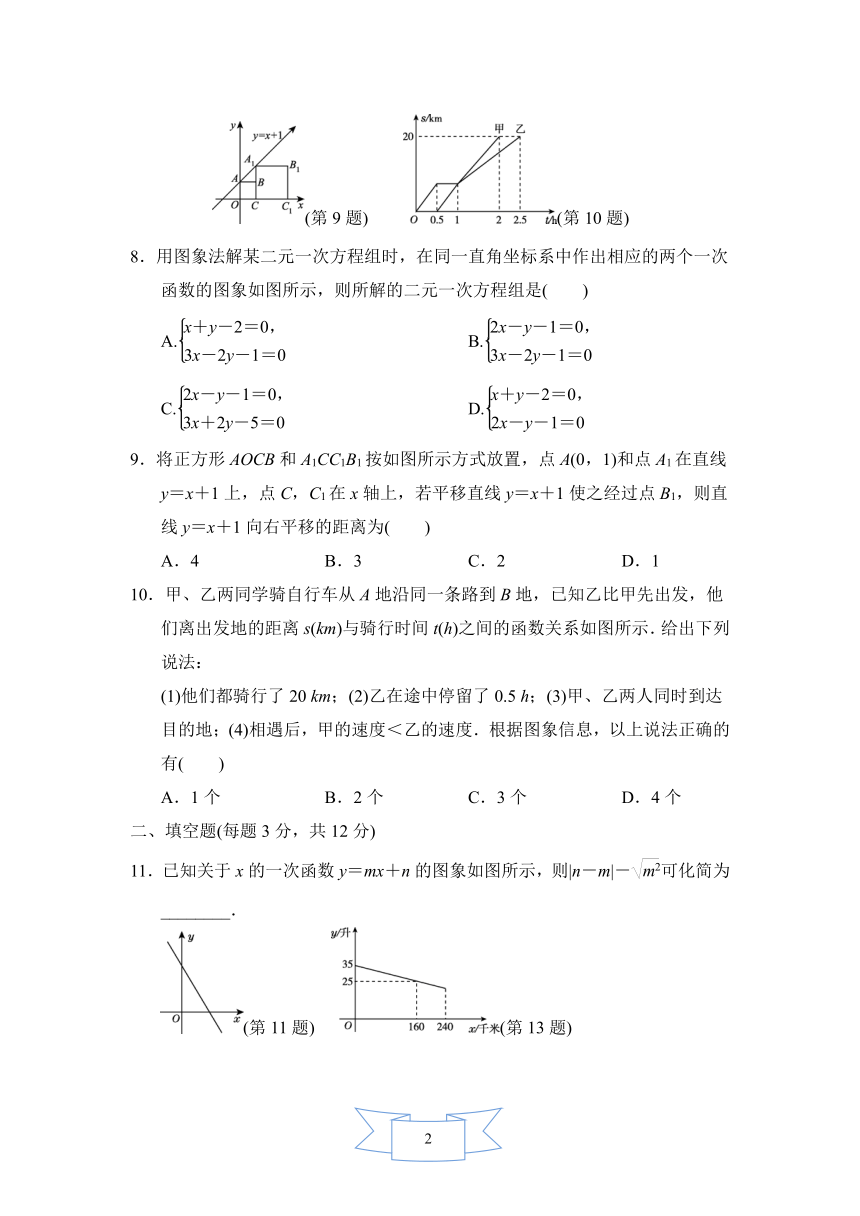
(第9题) (第10题)
8.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象如图所示,则所解的二元一次方程组是( )
A. B.
C. D.
9.将正方形AOCB和A1CC1B1按如图所示方式放置,点A(0,1)和点A1在直线y=x+1上,点C,C1在x轴上,若平移直线y=x+1使之经过点B1,则直线y=x+1向右平移的距离为( )
A.4 B.3 C.2 D.1
10.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)与骑行时间t(h)之间的函数关系如图所示.给出下列说法:
(1)他们都骑行了20 km;(2)乙在途中停留了0.5 h;(3)甲、乙两人同时到达目的地;(4)相遇后,甲的速度<乙的速度.根据图象信息,以上说法正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共12分)
11.已知关于x的一次函数y=mx+n的图象如图所示,则|n-m|-可化简为________.
(第11题) (第13题)
12.已知一次函数y=ax+b(a,b是常数,a≠0)的图象经过(-1,4),(2,-2)两点,下面说法中:(1)a=2,b=2;(2)函数图象经过(1,0);(3)不等式ax+b>0的解集是x<1;(4)不等式ax+b<0的解集是x<1;
正确的说法有________________.(请写出所有正确说法的序号)
13.李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是________升.
14.已知一次函数y=kx+b的图象与正比例函数y=x的图象交于点A,并与y轴交于点B(0,-4),三角形AOB的面积为6,则kb=________.
三、解答题(21,22题每题7分,23题8分,其余每题6分,共58分)
15.已知关于x的函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,它是一次函数?
(2)当m,n为何值时,它是正比例函数?
16.已知y+2与x-1成正比例,且x=3时,y=4.
(1)求y与x之间的函数表达式;
(2)当y=1时,求x的值.
17.已知一次函数的图象经过点(3,5)和点(-4,-9).
(1)求一次函数的表达式;
(2)求图象与坐标轴的交点坐标;
(3)求图象与坐标轴围成的三角形的面积S;
(4)若点(a,2)在该一次函数的图象上,求a的值.
18.如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,点P在坐标轴上,且PO=2AO.求三角形ABP的面积.
(第11题)
19.如图,直线l1,l2相交于点A,l1与x轴的交点坐标为(-1,0),l2与y轴的交点坐标为(0,-2),结合图象解答下列问题:
(1)求出直线l2表示的一次函数的表达式;
(2)当x为何值时,l1,l2表示的两个一次函数的函数值都大于0?
(第19题)
20.如图,已知直线y=-x+2与x轴、y轴分别交于点A,B,另一直线y=kx+b(k≠0)经过点C(1,0),且把三角形AOB分成两部分.
(1)若三角形AOB被分成的两部分面积相等,求经过C的直线解析式;
(2)若三角形AOB被分成的两部分面积比为1∶5,求经过C的直线解析式.
(第20题)
21.如图,点Q是正方形ABCD的边CD的中点,点P按A→B→C→Q的路线在正方形边上运动(点P不与点A,Q重合),正方形ABCD的边长为2.设点P经过的路程x为自变量,三角形APQ的面积为y.
(1)求y与x之间的函数表达式;
(2)画出此函数的图象.
(第21题)
22.漳州三宝之一“水仙花”畅销全球,某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
A地
B地
C地
运费/(元/件)
20
10
15
(1)设运往A地的水仙花为x件,总运费为y元,试写出y与x的函数表达式;
(2)若总运费不超过12 000元,则最多可运往A地多少件水仙花?
23.如图①是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(cm)与注水时间x(分钟)之间的关系如图②所示.根据图象提供的信息,解答下列问题:
(1)图②中折线ABC表示________槽中水的深度与注水时间的关系,线段DE表示________槽中水的深度与注水时间之间的关系,点B的纵坐标表示的实际意义是____________;
(2)注水多长时间时,甲、乙两个水槽中水的深度相同?
(3)若乙槽底面积为36cm2(壁厚不计),求乙槽中铁块的体积;
(4)若乙槽中铁块的体积为112cm3,求甲槽底面积(壁厚不计).(直接写出结果)
(第23题)
答案
一、1.B 2.C
3.C 点拨:因为y=-x+b中k=-1<0,所以y随x的增大而减小,因为x1<x2,所以y1>y2.
4.A 5.D
6.D 点拨:设这条直线对应的函数表达式为y=kx+b.把(-3,-1),(1,1)分别代入y=kx+b中,得解得
所以y=0.5x+0.5.当x=3时,y=2,所以(3,2)在直线y=0.5x+0.5上,当x=4时,y=2.5,所以(4,3)不在直线y=0.5x+0.5上.
7.D 8.D
9.C 点拨:已知点A(0,1)和正方形AOCB,即可得C(1,0),将x=1代入y=x+1可得y=2,所以A1(1,2),又因正方形A1CC1B1,可得B1(3,2),设平移后的直线为y=(x-x0)+1,将B代入可求得x0=2,即直线y=x+1向右平移的距离为2.故选C.
10.B 点拨:由题图可获取的信息是:他们都骑行了20 km;乙在途中停留了0.5 h;相遇后,甲的速度>乙的速度,甲比乙早0.5 h到达目的地,所以(1)(2)正确.
二、11.n 12.(2)(3)
13.20 点拨:先运用待定系数法求出y与x之间的函数表达式,然后把x=240代入函数表达式就可以求出y的值,从而得出剩余油量.
14.4或- 点拨:把(0,-4)代入y=kx+b,得到b=-4;由题意得OB=4,设A的横坐标是m,则根据三角形AOB的面积为6,得到 ×4×|m|=6,解得m=±3.把x=±3代入y=x,解得y=±1,则A的坐标是(3,1)或(-3,-1).当A的坐标是(3,1)时,代入y=kx-4,可得到k=,则kb=×(-4)=-;当A的坐标是(-3,-1)时,代入y=kx-4,可得到k=-1,则kb=(-1)×(-4)=4.
三、15.解:(1)由题意得,2-|m|=1且m+1≠0,解得m=1,所以当m=1,n为任意实数时,此函数是一次函数.
(2)由题意得,2-|m|=1,m+1≠0且n+4=0,解得m=1,n=-4,即当m=1,n=-4时,此函数是正比例函数.
16.解:(1)设y+2=k(x-1),把x=3,y=4代入得:4+2=k(3-1),解得k=3,则y与x之间的函数表达式是:y+2=3(x-1),即y=3x-5.(2)当y=1,即3x-5=1时,解得x=2.
17.解:(1)设一次函数的表达式为y=kx+b,把(3,5),(-4,-9)分别代入表达式得
解得
所以一次函数的表达式为y=2x-1.
(2)当x=0时,y=-1,
当y=0时,即2x-1=0,
解得x=,
所以图象与坐标轴的交点坐标为(0,-1),.
(3)S=××|-1|=.
(4)因为点(a,2)在该一次函数的图象上,所以2a-1=2,所以a=.
18.解:∵直线y=2x+4与x轴交于点A,与y轴交于点B,
∴A(-2,0),B(0,4).
当点P在x轴的正半轴上时,
S三角形ABP=S三角形AOB+S三角形OBP
=×2×4+×4×4=12;
当点P在x轴的负半轴上时,
S三角形ABP=S三角形OBP-S三角形AOB
=×4×4-×2×4=4;
当点P在y轴的正半轴上时,点P与点B重合,三角形ABP不存在;
当点P在y轴的负半轴上时,
S三角形ABP=S三角形OAP+S三角形AOB
=×2×4+×2×4=8.
综上,三角形ABP的面积为4或8或12.
19.解:(1)设直线l2表示的一次函数表达式为y=kx+b,
∵x=0时,y=-2;x=2时,y=3.
∴∴
∴直线l2表示的一次函数表达式是y=x-2.
(2)从图象可以知道,当x>-1时,直线l2表示的一次函数的函数值大于0.令x-2=0,得x=,
∴当x>时,直线l2表示的一次函数的函数值大于0.
∴当x>时,l1,l2表示的两个一次函数的函数值都大于0.
20.解:(1)过B(0,2),C(1,0)的直线解析式为y=-2x+2;
(2)设y=kx+b与OB交于M(0,h),分三角形AOB面积为1∶5,得S三角形OMC=S三角形OAB,则×1×h=××2×2, 解得h=,所以M(0,).经过点M作直线MN∥OA交AB于N(a,),则S三角形OMC=S三角形CAN,因为N(a,)在直线y=-x+2上,所以a=,故N(,).
∴直线CM:y=-x+,
直线CN:y=2x-2.
21.解:(1)当点P在AB上时,即当0<x≤2时,y=·x·2=x;当点P在BC上时,即当2<x≤4时,y=2×2-×1×2-×2×(x-2)-×1 ×(4-x)=-x+3;当点P在CQ上时,即当4<x<5时,y=×2×(5-x)=-x+5.综上可知,y与x之间的函数表达式为y=
(2)画图象略.
22.解:(1)由运往A地的水仙花为x件,知运往C地的水仙花为3x件,则运往B地的水仙花为(800-4x)件,由题意得,y=20x+10(800-4x)+45x,即y=25x+8 000.
(2)因为y≤12 000,所以25x+8 000≤12 000,解得:x≤160,
所以若总运费不超过12 000元,则最多可运往A地160件水仙花.
23.解:(1)乙;甲;铁块的高度为14 cm
(2)设直线DE的表达式为y=k1x+b1,则
∴
∴DE的表达式为y=-2x+12.
设直线AB的表达式为y=k2x+b2,则∴
∴AB的表达式为y=3x+2.
由题意得解得∴注水2分钟时,甲、乙两水槽中水的深度相同.
(3)∵水由甲槽匀速注入乙槽,∴乙槽前4分钟注入水的体积是后2分钟的2倍.
设乙槽底面积与铁块底面积之差为S,则(14-2)S=2×36×(19-14),
解得S=30 cm2.
∴铁块底面积为36-30=6 (cm2).
∴铁块的体积为6×14=84 (cm3).
(4)甲槽底面积为60 cm2.
一、选择题(每题3分,共30分)
1.下列图象中,表示y不是x的函数的是( )
2.函数y=中自变量x的取值范围为( )
A.x≥0 B.x≥- C.x≥ D.x≤-
3.点(x1,y1),(x2,y2)在直线y=-x+b上,若x1<x2,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.无法确定
4.将函数y=-3x的图象沿y轴向上平移2个单位后,所得图象对应的函数表达式为( )
A.y=-3x+2 B.y=-3x-2
C.y=-3(x+2) D.y=-3(x-2)
5.直线y=x-1的图象经过的象限是( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
6.下列四个点中,有三个点在同一条直线上,不在这条直线上的点是( )
A.(-3,-1) B.(1,1) C.(3,2) D.(4,3)
7.如图所示,函数y1=|x|和y2=x+的图象相交于(-1,1),(2,2)两点.当y1>y2时,x的取值范围是( )
A.x<-1 B.-1<x<2
C.x>2 D.x<-1或x>2
(第7题) (第8题)
(第9题) (第10题)
8.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象如图所示,则所解的二元一次方程组是( )
A. B.
C. D.
9.将正方形AOCB和A1CC1B1按如图所示方式放置,点A(0,1)和点A1在直线y=x+1上,点C,C1在x轴上,若平移直线y=x+1使之经过点B1,则直线y=x+1向右平移的距离为( )
A.4 B.3 C.2 D.1
10.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)与骑行时间t(h)之间的函数关系如图所示.给出下列说法:
(1)他们都骑行了20 km;(2)乙在途中停留了0.5 h;(3)甲、乙两人同时到达目的地;(4)相遇后,甲的速度<乙的速度.根据图象信息,以上说法正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共12分)
11.已知关于x的一次函数y=mx+n的图象如图所示,则|n-m|-可化简为________.
(第11题) (第13题)
12.已知一次函数y=ax+b(a,b是常数,a≠0)的图象经过(-1,4),(2,-2)两点,下面说法中:(1)a=2,b=2;(2)函数图象经过(1,0);(3)不等式ax+b>0的解集是x<1;(4)不等式ax+b<0的解集是x<1;
正确的说法有________________.(请写出所有正确说法的序号)
13.李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是________升.
14.已知一次函数y=kx+b的图象与正比例函数y=x的图象交于点A,并与y轴交于点B(0,-4),三角形AOB的面积为6,则kb=________.
三、解答题(21,22题每题7分,23题8分,其余每题6分,共58分)
15.已知关于x的函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,它是一次函数?
(2)当m,n为何值时,它是正比例函数?
16.已知y+2与x-1成正比例,且x=3时,y=4.
(1)求y与x之间的函数表达式;
(2)当y=1时,求x的值.
17.已知一次函数的图象经过点(3,5)和点(-4,-9).
(1)求一次函数的表达式;
(2)求图象与坐标轴的交点坐标;
(3)求图象与坐标轴围成的三角形的面积S;
(4)若点(a,2)在该一次函数的图象上,求a的值.
18.如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,点P在坐标轴上,且PO=2AO.求三角形ABP的面积.
(第11题)
19.如图,直线l1,l2相交于点A,l1与x轴的交点坐标为(-1,0),l2与y轴的交点坐标为(0,-2),结合图象解答下列问题:
(1)求出直线l2表示的一次函数的表达式;
(2)当x为何值时,l1,l2表示的两个一次函数的函数值都大于0?
(第19题)
20.如图,已知直线y=-x+2与x轴、y轴分别交于点A,B,另一直线y=kx+b(k≠0)经过点C(1,0),且把三角形AOB分成两部分.
(1)若三角形AOB被分成的两部分面积相等,求经过C的直线解析式;
(2)若三角形AOB被分成的两部分面积比为1∶5,求经过C的直线解析式.
(第20题)
21.如图,点Q是正方形ABCD的边CD的中点,点P按A→B→C→Q的路线在正方形边上运动(点P不与点A,Q重合),正方形ABCD的边长为2.设点P经过的路程x为自变量,三角形APQ的面积为y.
(1)求y与x之间的函数表达式;
(2)画出此函数的图象.
(第21题)
22.漳州三宝之一“水仙花”畅销全球,某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
A地
B地
C地
运费/(元/件)
20
10
15
(1)设运往A地的水仙花为x件,总运费为y元,试写出y与x的函数表达式;
(2)若总运费不超过12 000元,则最多可运往A地多少件水仙花?
23.如图①是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(cm)与注水时间x(分钟)之间的关系如图②所示.根据图象提供的信息,解答下列问题:
(1)图②中折线ABC表示________槽中水的深度与注水时间的关系,线段DE表示________槽中水的深度与注水时间之间的关系,点B的纵坐标表示的实际意义是____________;
(2)注水多长时间时,甲、乙两个水槽中水的深度相同?
(3)若乙槽底面积为36cm2(壁厚不计),求乙槽中铁块的体积;
(4)若乙槽中铁块的体积为112cm3,求甲槽底面积(壁厚不计).(直接写出结果)
(第23题)
答案
一、1.B 2.C
3.C 点拨:因为y=-x+b中k=-1<0,所以y随x的增大而减小,因为x1<x2,所以y1>y2.
4.A 5.D
6.D 点拨:设这条直线对应的函数表达式为y=kx+b.把(-3,-1),(1,1)分别代入y=kx+b中,得解得
所以y=0.5x+0.5.当x=3时,y=2,所以(3,2)在直线y=0.5x+0.5上,当x=4时,y=2.5,所以(4,3)不在直线y=0.5x+0.5上.
7.D 8.D
9.C 点拨:已知点A(0,1)和正方形AOCB,即可得C(1,0),将x=1代入y=x+1可得y=2,所以A1(1,2),又因正方形A1CC1B1,可得B1(3,2),设平移后的直线为y=(x-x0)+1,将B代入可求得x0=2,即直线y=x+1向右平移的距离为2.故选C.
10.B 点拨:由题图可获取的信息是:他们都骑行了20 km;乙在途中停留了0.5 h;相遇后,甲的速度>乙的速度,甲比乙早0.5 h到达目的地,所以(1)(2)正确.
二、11.n 12.(2)(3)
13.20 点拨:先运用待定系数法求出y与x之间的函数表达式,然后把x=240代入函数表达式就可以求出y的值,从而得出剩余油量.
14.4或- 点拨:把(0,-4)代入y=kx+b,得到b=-4;由题意得OB=4,设A的横坐标是m,则根据三角形AOB的面积为6,得到 ×4×|m|=6,解得m=±3.把x=±3代入y=x,解得y=±1,则A的坐标是(3,1)或(-3,-1).当A的坐标是(3,1)时,代入y=kx-4,可得到k=,则kb=×(-4)=-;当A的坐标是(-3,-1)时,代入y=kx-4,可得到k=-1,则kb=(-1)×(-4)=4.
三、15.解:(1)由题意得,2-|m|=1且m+1≠0,解得m=1,所以当m=1,n为任意实数时,此函数是一次函数.
(2)由题意得,2-|m|=1,m+1≠0且n+4=0,解得m=1,n=-4,即当m=1,n=-4时,此函数是正比例函数.
16.解:(1)设y+2=k(x-1),把x=3,y=4代入得:4+2=k(3-1),解得k=3,则y与x之间的函数表达式是:y+2=3(x-1),即y=3x-5.(2)当y=1,即3x-5=1时,解得x=2.
17.解:(1)设一次函数的表达式为y=kx+b,把(3,5),(-4,-9)分别代入表达式得
解得
所以一次函数的表达式为y=2x-1.
(2)当x=0时,y=-1,
当y=0时,即2x-1=0,
解得x=,
所以图象与坐标轴的交点坐标为(0,-1),.
(3)S=××|-1|=.
(4)因为点(a,2)在该一次函数的图象上,所以2a-1=2,所以a=.
18.解:∵直线y=2x+4与x轴交于点A,与y轴交于点B,
∴A(-2,0),B(0,4).
当点P在x轴的正半轴上时,
S三角形ABP=S三角形AOB+S三角形OBP
=×2×4+×4×4=12;
当点P在x轴的负半轴上时,
S三角形ABP=S三角形OBP-S三角形AOB
=×4×4-×2×4=4;
当点P在y轴的正半轴上时,点P与点B重合,三角形ABP不存在;
当点P在y轴的负半轴上时,
S三角形ABP=S三角形OAP+S三角形AOB
=×2×4+×2×4=8.
综上,三角形ABP的面积为4或8或12.
19.解:(1)设直线l2表示的一次函数表达式为y=kx+b,
∵x=0时,y=-2;x=2时,y=3.
∴∴
∴直线l2表示的一次函数表达式是y=x-2.
(2)从图象可以知道,当x>-1时,直线l2表示的一次函数的函数值大于0.令x-2=0,得x=,
∴当x>时,直线l2表示的一次函数的函数值大于0.
∴当x>时,l1,l2表示的两个一次函数的函数值都大于0.
20.解:(1)过B(0,2),C(1,0)的直线解析式为y=-2x+2;
(2)设y=kx+b与OB交于M(0,h),分三角形AOB面积为1∶5,得S三角形OMC=S三角形OAB,则×1×h=××2×2, 解得h=,所以M(0,).经过点M作直线MN∥OA交AB于N(a,),则S三角形OMC=S三角形CAN,因为N(a,)在直线y=-x+2上,所以a=,故N(,).
∴直线CM:y=-x+,
直线CN:y=2x-2.
21.解:(1)当点P在AB上时,即当0<x≤2时,y=·x·2=x;当点P在BC上时,即当2<x≤4时,y=2×2-×1×2-×2×(x-2)-×1 ×(4-x)=-x+3;当点P在CQ上时,即当4<x<5时,y=×2×(5-x)=-x+5.综上可知,y与x之间的函数表达式为y=
(2)画图象略.
22.解:(1)由运往A地的水仙花为x件,知运往C地的水仙花为3x件,则运往B地的水仙花为(800-4x)件,由题意得,y=20x+10(800-4x)+45x,即y=25x+8 000.
(2)因为y≤12 000,所以25x+8 000≤12 000,解得:x≤160,
所以若总运费不超过12 000元,则最多可运往A地160件水仙花.
23.解:(1)乙;甲;铁块的高度为14 cm
(2)设直线DE的表达式为y=k1x+b1,则
∴
∴DE的表达式为y=-2x+12.
设直线AB的表达式为y=k2x+b2,则∴
∴AB的表达式为y=3x+2.
由题意得解得∴注水2分钟时,甲、乙两水槽中水的深度相同.
(3)∵水由甲槽匀速注入乙槽,∴乙槽前4分钟注入水的体积是后2分钟的2倍.
设乙槽底面积与铁块底面积之差为S,则(14-2)S=2×36×(19-14),
解得S=30 cm2.
∴铁块底面积为36-30=6 (cm2).
∴铁块的体积为6×14=84 (cm3).
(4)甲槽底面积为60 cm2.
