第12章 一次函数 全章热门考点综合应用 课件
文档属性
| 名称 | 第12章 一次函数 全章热门考点综合应用 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 369.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-22 00:00:00 | ||
图片预览








文档简介
课件28张PPT。全章热门考点综合应用第十二章 一次函数概念1 函数
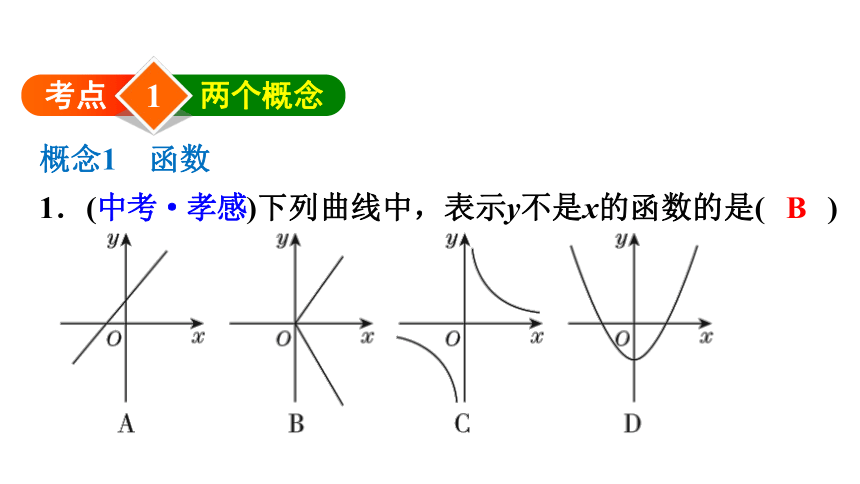
1.(中考·孝感)下列曲线中,表示y不是x的函数的是( )1考点两个概念B2.(1)(中考·鞍山)函数y= 中,自变量x的取值范围是( )
A.x≥-2 B.x>-2 C.x≤-2 D.x<-2
(2)下列函数中,自变量x的取值范围是x≥3的是( )
A. B. C.x-3 D.
AD(3)函数 中,自变量x的取值范围是( )
A.x≤2 B.x=3 C.x<2 D.x≥2且x≠3A概念2 一次函数
3.当m,n为何值时,y=(5m-3)x2-n+(m+n)是关于x的一次函数?当m,n为何值时,y是关于x的正比例函数?解:若y=(5m-3)x2-n+(m+n)是关于x的一次函数,
则有 解得 所以当m≠ 且n=1时,
y=(5m-3)x2-n+(m+n)是关于x的一次函数.若y=(5m
-3)x2-n+(m+n)是关于x的正比例函数,则有
解得 所以当m=-1且n=1时,y=(5m-3)x2-n+(m+n)是关于x的正比例函数.4.(中考·阜新)对于一次函数y=kx+k-1(k≠0),下列叙述正确的是( )
A.当0B.当k>0时,y随x的增大而减小
C.当k<1时,函数图象一定交于y轴的负半轴
D.函数图象一定经过点(-1,-2)2考点一个图象——一次函数的图象C5.已知一次函数的表达式是y=(k-2)x+12-3k.
(1)当图象与y轴的交点位于原点下方时,判断函数值随着自变量的增大而变化的趋势;
(2)如果函数值随着自变量的增大而增大,且函数图象与y轴的交点位于原点上方,确定满足条件的正整数k的值.3考点一个性质——一次函数的性质解:(1)因为图象与y轴的交点位于原点下方,即点(0,12-3k)位于原点下方,所以12-3k<0,解得k>4.所以k-2>4-2>0,所以函数值随着自变量的增大而增大.
(2)因为函数值随着自变量的增大而增大,所以k-2>0,解得k>2.因为函数图象与y轴的交点位于原点上方,所以12-3k>0,解得k<4.所以k的取值范围为26.下列函数中,哪些是一次函数?哪些是正比例函数?
①y=-2x-1;②y= x;③y= ;④y=-x2-1;
⑤2x-y=0;⑥y=-2(x-1).4考点四个关系解:一次函数:①②⑤⑥;正比例函数:②⑤.关系2 一次函数与一元一次方程的关系
7.如图,在平面直角坐标系xOy中,直线y=x+1与y=-
x+3交于点A ( ) 两直线分别交x轴于点B和点C.求:
(1)点B,C的坐标;
(2)三角形ABC的面积.解:(1)由x+1=0,得x=-1,所以点B的坐标是(-1,0).
由- x+3=0,得x=4,所以点C的坐标是(4,0).
(2)因为BC=4-(-1)=5,点A到x轴的距离为 ,所以S三角形ABC= ×5× = .关系3 一次函数与二元一次方程(组)的关系
8.(蚌埠期末)如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组 的解是( )
A. B.
C. D.A关系4 一次函数与一元一次不等式(组)的关系
9.在同一平面直角坐标系中,画出一次函数y1=2x-4,y2=x+1的图象,根据图象求:
(1)二元一次方程组 的解;
(2)一元一次不等式组 的解集.解:图象略.
(1)由图象知,直线y=2x-4与y=x+1的交点坐标为(5,6).
所以方程组 的解为
(2)由图象知,不等式组2x-4>0,x+1>0的解集为x>2.10.如图,一个正比例函数图象与一个一次函数图象交于点A(3,4),且一次函数的图象与y轴相交于点B(0,-5).求:
(1)这两个函数的表达式;
(2)三角形AOB的面积.5考点一个方法——待定系数法解:(1)设正比例函数的表达式为y=k1x,一次函数的表达式为y=k2x+b.把A(3,4)的坐标代入y=k1x,得k1= ;把A(3,4),B(0,-5)的坐标分别代入y=k2x+b,解得k2=3,b=-5.故正比例函数的表达式为y= x,一次函数的表达式为y=3x-5.解:(2)因为A点横坐标为3,所以A点到OB的距离为3.
又因为B点纵坐标为-5,所以OB=5.
所以三角形AOB的面积为 ×5×3=7.5.应用1 给出表达式(或图象)解实际问题
11.(中考·河南)某游泳馆普通票价20元/张,暑期为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费;
②银卡售价150元/张,每次凭卡另收10元.6考点两个应用暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数表达式;
(2)在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A,B,C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.解:(1)银卡:y=10x+150;普通票:y=20x.
(2)把x=0代入y=10x+150,得y=150.所以A(0,150).
由 得 所以B(15,300).把y=600代入y=10x+150,得x=45.所以C(45,600).解:(3)当045时,选择购买金卡更合算.应用2 只给语言叙述或图表情境解实际问题
12.为改善生态环境,防止水土流失,某村计划在河堤坡面种植白杨树,现有甲、乙两家林场可提供相同质量的白杨树苗,其具体销售方案如下:设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲 (元),y乙(元).
(1)该村需要购买1 500棵白杨树苗,若都在甲林场购买所需费用为___元,若都在乙林场购买所需费用为___元;
(2)分别求出y甲,y乙与x之间的函数表达式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?解:(1)5 900;6 000
(2)当0≤x≤1 000时,y甲=4x;当x>1 000时,y甲=4 000+3.8(x-1 000)=3.8x+200.所以 当0≤x≤2 000时,y乙=4x;当x>2 000时,y乙=8 000+3.6(x-2 000)=3.6x+800.所以解:(3)由题意,得:当0≤x≤1 000时,两家林场白杨树苗销售价格一样,所以到两家林场购买树苗所需费用一样.当1 0002 000时,y甲=3.8x+200,y乙=3.6x+800,当y甲=y乙时,3.8x+200=3.6x+800,解得x=3 000,所以当x=3 000时,到两家林场购买树苗所需费用一样;解:当y甲y乙时,3.8x+200>3.6x+800,解得x>3 000,所以当x>3 000时,到乙林场购买树苗合算.综上所述,当0≤x≤1 000或x=3 000时,到两家林场购买树苗所需费用一样;当1 0003 000时,到乙林场购买树苗合算.
1.(中考·孝感)下列曲线中,表示y不是x的函数的是( )1考点两个概念B2.(1)(中考·鞍山)函数y= 中,自变量x的取值范围是( )
A.x≥-2 B.x>-2 C.x≤-2 D.x<-2
(2)下列函数中,自变量x的取值范围是x≥3的是( )
A. B. C.x-3 D.
AD(3)函数 中,自变量x的取值范围是( )
A.x≤2 B.x=3 C.x<2 D.x≥2且x≠3A概念2 一次函数
3.当m,n为何值时,y=(5m-3)x2-n+(m+n)是关于x的一次函数?当m,n为何值时,y是关于x的正比例函数?解:若y=(5m-3)x2-n+(m+n)是关于x的一次函数,
则有 解得 所以当m≠ 且n=1时,
y=(5m-3)x2-n+(m+n)是关于x的一次函数.若y=(5m
-3)x2-n+(m+n)是关于x的正比例函数,则有
解得 所以当m=-1且n=1时,y=(5m-3)x2-n+(m+n)是关于x的正比例函数.4.(中考·阜新)对于一次函数y=kx+k-1(k≠0),下列叙述正确的是( )
A.当0
C.当k<1时,函数图象一定交于y轴的负半轴
D.函数图象一定经过点(-1,-2)2考点一个图象——一次函数的图象C5.已知一次函数的表达式是y=(k-2)x+12-3k.
(1)当图象与y轴的交点位于原点下方时,判断函数值随着自变量的增大而变化的趋势;
(2)如果函数值随着自变量的增大而增大,且函数图象与y轴的交点位于原点上方,确定满足条件的正整数k的值.3考点一个性质——一次函数的性质解:(1)因为图象与y轴的交点位于原点下方,即点(0,12-3k)位于原点下方,所以12-3k<0,解得k>4.所以k-2>4-2>0,所以函数值随着自变量的增大而增大.
(2)因为函数值随着自变量的增大而增大,所以k-2>0,解得k>2.因为函数图象与y轴的交点位于原点上方,所以12-3k>0,解得k<4.所以k的取值范围为2
①y=-2x-1;②y= x;③y= ;④y=-x2-1;
⑤2x-y=0;⑥y=-2(x-1).4考点四个关系解:一次函数:①②⑤⑥;正比例函数:②⑤.关系2 一次函数与一元一次方程的关系
7.如图,在平面直角坐标系xOy中,直线y=x+1与y=-
x+3交于点A ( ) 两直线分别交x轴于点B和点C.求:
(1)点B,C的坐标;
(2)三角形ABC的面积.解:(1)由x+1=0,得x=-1,所以点B的坐标是(-1,0).
由- x+3=0,得x=4,所以点C的坐标是(4,0).
(2)因为BC=4-(-1)=5,点A到x轴的距离为 ,所以S三角形ABC= ×5× = .关系3 一次函数与二元一次方程(组)的关系
8.(蚌埠期末)如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组 的解是( )
A. B.
C. D.A关系4 一次函数与一元一次不等式(组)的关系
9.在同一平面直角坐标系中,画出一次函数y1=2x-4,y2=x+1的图象,根据图象求:
(1)二元一次方程组 的解;
(2)一元一次不等式组 的解集.解:图象略.
(1)由图象知,直线y=2x-4与y=x+1的交点坐标为(5,6).
所以方程组 的解为
(2)由图象知,不等式组2x-4>0,x+1>0的解集为x>2.10.如图,一个正比例函数图象与一个一次函数图象交于点A(3,4),且一次函数的图象与y轴相交于点B(0,-5).求:
(1)这两个函数的表达式;
(2)三角形AOB的面积.5考点一个方法——待定系数法解:(1)设正比例函数的表达式为y=k1x,一次函数的表达式为y=k2x+b.把A(3,4)的坐标代入y=k1x,得k1= ;把A(3,4),B(0,-5)的坐标分别代入y=k2x+b,解得k2=3,b=-5.故正比例函数的表达式为y= x,一次函数的表达式为y=3x-5.解:(2)因为A点横坐标为3,所以A点到OB的距离为3.
又因为B点纵坐标为-5,所以OB=5.
所以三角形AOB的面积为 ×5×3=7.5.应用1 给出表达式(或图象)解实际问题
11.(中考·河南)某游泳馆普通票价20元/张,暑期为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费;
②银卡售价150元/张,每次凭卡另收10元.6考点两个应用暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数表达式;
(2)在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A,B,C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.解:(1)银卡:y=10x+150;普通票:y=20x.
(2)把x=0代入y=10x+150,得y=150.所以A(0,150).
由 得 所以B(15,300).把y=600代入y=10x+150,得x=45.所以C(45,600).解:(3)当0
12.为改善生态环境,防止水土流失,某村计划在河堤坡面种植白杨树,现有甲、乙两家林场可提供相同质量的白杨树苗,其具体销售方案如下:设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲 (元),y乙(元).
(1)该村需要购买1 500棵白杨树苗,若都在甲林场购买所需费用为___元,若都在乙林场购买所需费用为___元;
(2)分别求出y甲,y乙与x之间的函数表达式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?解:(1)5 900;6 000
(2)当0≤x≤1 000时,y甲=4x;当x>1 000时,y甲=4 000+3.8(x-1 000)=3.8x+200.所以 当0≤x≤2 000时,y乙=4x;当x>2 000时,y乙=8 000+3.6(x-2 000)=3.6x+800.所以解:(3)由题意,得:当0≤x≤1 000时,两家林场白杨树苗销售价格一样,所以到两家林场购买树苗所需费用一样.当1 000
