物理:3.5《牛顿运动定律的应用》测试(教科版必修1)
文档属性
| 名称 | 物理:3.5《牛顿运动定律的应用》测试(教科版必修1) |
|
|
| 格式 | zip | ||
| 文件大小 | 40.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2014-03-14 00:00:00 | ||
图片预览


文档简介
牛顿运动定律的应用 专题训练
(时间60分钟,赋分100分)
训练指要
本套试题训练和考查的重点是:进一步理解和掌握牛顿运动定律.能熟练地运用牛顿定律解题,并能解答较简单的连接体问题.第13题和第15题为创新题.第13题有利于提高学生的思维判断能力.第15题有利于提高学生的审题能力.
一、选择题(每小题5分,共40分)
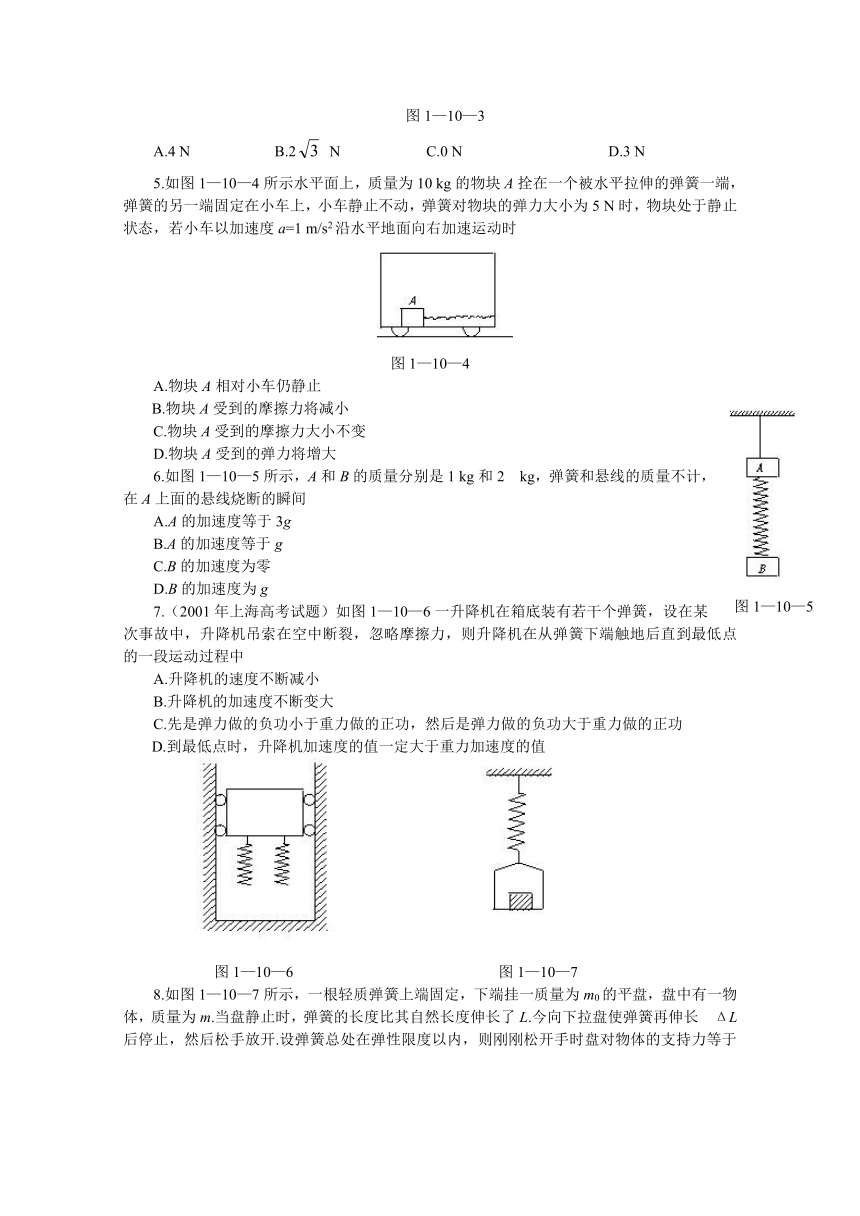
1.如图1—10—1所示,悬挂于小车里的小球偏离竖直方向θ角,则小车可能的运动情况是
图1—10—1
A.向右加速运动 B.向右减速运动 C.向左加速运动 D.向左减速运动
2.如图1—10—2所示为一光滑竖直圆槽,AP、BP、CP为通过最低点P与水平面分别成30°、45°、60°角的三个光滑斜面,与圆相交于A、B、C点.若一物体由静止分别从A、B、C滑至P点所需的时间为t1,t2,t3,则
图1—10—2
A.t1<t2<t3 B.t1>t2>t3 C.t1=t2=t3 D.t1=t2<t3
3.在升降机内的地板上放一秤,一人让在秤上,用W表示升降机匀速运动时秤的示数,W1和W2分别表示升降机以大小为a的加速度加速上升和减速下降时称的示数,则
A.W2<W<W1 B.W<W1 W<W2 C.W<W1=W2 D.W>W1 W>W2
4.如图1—10—3所示,在托盘测力计的托盘内固定一个倾角为30°的光滑斜面,现将一个重4 N的物体放在斜面上,让它自由滑下,那么测力计因4 N物体的存在,而增加的读数是
图1—10—3
A.4 N B.2 N C.0 N D.3 N
5.如图1—10—4所示水平面上,质量为10 kg的物块A拴在一个被水平拉伸的弹簧一端,弹簧的另一端固定在小车上,小车静止不动,弹簧对物块的弹力大小为5 N时,物块处于静止状态,若小车以加速度a=1 m/s2沿水平地面向右加速运动时
图1—10—4
A.物块A相对小车仍静止
B.物块A受到的摩擦力将减小
C.物块A受到的摩擦力大小不变
D.物块A受到的弹力将增大
6.如图1—10—5所示,A和B的质量分别是1 kg和2 kg,弹簧和悬线的质量不计,在A上面的悬线烧断的瞬间
A.A的加速度等于3g
B.A的加速度等于g
C.B的加速度为零
D.B的加速度为g
7.(2001年上海高考试题)如图1—10—6一升降机在箱底装有若干个弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中
A.升降机的速度不断减小
B.升降机的加速度不断变大
C.先是弹力做的负功小于重力做的正功,然后是弹力做的负功大于重力做的正功
D.到最低点时,升降机加速度的值一定大于重力加速度的值
图1—10—6 图1—10—7
8.如图1—10—7所示,一根轻质弹簧上端固定,下端挂一质量为m0的平盘,盘中有一物体,质量为m.当盘静止时,弹簧的长度比其自然长度伸长了L.今向下拉盘使弹簧再伸长 ΔL后停止,然后松手放开.设弹簧总处在弹性限度以内,则刚刚松开手时盘对物体的支持力等于
A.(1+)mg B.(1+)(m+m0)g
C. mg D. (m+m0)g
二、填空题(每小题6分,共24分)
9.汽车在水平公路上做直线运动,它的功率保持不变,当汽车的速度为4 m/s时,加速度为0.4 m/s2,汽车所受阻力恒为车重的0.01倍,若取g=10 m/s2,汽车行驶的最大速度为_______ m/s.
10.已知质量为m的木块的大小为F的水平拉力作用下沿粗糙水平地面做匀加速直线运动,加速度为a,则木块与地面之间的动摩擦因数为_______.若在木块上再施加一个与水平拉力F在同一竖直平面内的推力,而不改变木块的加速度的大小和方向,则此推力与水平拉力F的夹角为_______.
11.总质量为M的热气球由于故障在空中以速度v0匀速下降.为了阻止继续下降,在t=0时刻,从热气球中释放了一个质量为m的沙袋.不计空气阻力,当t=________时,热气球停止下降,这时沙袋的速度为________.
12.一辆小车在水平恒力F作用下,由静止开始在水平面上匀加速运动t1 s后撤去F,小车再经过t2 s停下.则小车加速阶段的位移s1与减速阶段的位移s2之比s1∶s2=______;小车牵引力F与所受的摩擦力Ff之比F∶Ff=______.
三、计算题(共36分)
13.(12分)如图1—10—8所示,一质量为m的物体系于长度分别为l1、l2的两根细线上,l1的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态.现将l2线剪断,求剪断瞬时物体的加速度.
图1—10—8
(1)下面是某同学对该题的一种解法:
解:设l1线上拉力为T1,l2线上拉力为T2,重力为mg,物体在三力作用下保持平衡
T1cosθ=mg,T1sinθ=T2,T2=mgtanθ
剪断线的瞬间,T2突然消失,物体即在T2反方向获得加速度.因为mgtanθ=ma,所以加速度a=gtanθ,方向与T2反方向.
你认为这个结果正确吗 请对该解法作出评价并说明理由.
(2)若将图1—10—8中的细线l1改为长度相同、质量不计的轻弹簧,如图1—10—9所示,其他条件不变,求解的步骤和结果与(1)完全相同,即a=gtanθ,你认为这个结果正确吗 请说明理由.
图1—10—9
14.(12分)一弹簧秤的秤盘质量M=1.5 kg,盘内放一物体P,物体P的质量m=10.5 kg,弹簧质量不计,其劲度系数为k=800N/m,系统处于静止状态,如图1—10—10所示.现给P施加一个竖直向上的力F,使P从静止开始向上做匀加速运动,已知在头0.2 s内F是变力,在0.2 s以后是恒力.求F的最小值和最大值各是多少 (g=10 m/s2)
图1—10—10
15.(12分)2001年9月11日,美国遭受了历史上规模最大、损失最为惨重的恐怖主义袭击,恐怖分子劫持客机分别撞击了纽约的“世贸大楼”和华盛顿的“五角大楼”.其中一架客机拦腰撞到世贸大楼的南部塔楼第60层地方,并引起巨大爆炸,大约1 h后,南部塔楼部分轰然倒塌(高约245 m),灰尘和残骸四处飞溅,300多名救援警察和消防人员没来得及逃生.
我们不妨设置一个情境:当处于倒塌部分正下方的地面人员,看到一块质量约为4× 103 kg的楼墙块竖直倒下的同时到作出反应开始逃离需0.2 s的时间,逃离的安全区域为离大厦100 m外(实际的安全区要更远).设该坠落块与地面作用时间为0.05 s,不计空气阻力,g取10 m/s2.求:
(1)地面人员要逃离大厦到安全区至少要以多大速度奔跑?(忽略人的加速时间,百米短跑世界记录为9″79)
(2)该坠落块对地产生的平均作用力多大?
(3)由于爆炸引起地表震动,设产生的纵波的传播速率vp=9.1 km/s,横波的传播速率vs=3.1 km/s,设在某处的地震勘测中心记录到两种不同震感之间的时间间隔Δt0=5 s,那么观测记录者与震源之间的距离s为多少千米?
参考答案
一、1.AD 2.C 3.BC 4.D 5.AC 6.AC 7.CD?
8.A 以盘和重物为一个整体加以隔离,平衡时?
kL=(m+m0)g,k=.?
用手向下拉,弹簧共伸长L+ΔL,弹力F=k(L+ΔL)?
手的瞬时,根据牛顿第二定律F-(m+m0)g=(m+m0)α.把F值代入得
(L+ΔL)-(m+m0)g=(m+m0)a?
a=g,方向向上.?
隔离盘中物体,设盘对物体的支持力为N,由牛顿第二定律N-mg=ma?
故N=mg+ma=mg+mg=(1+)mg,向上.?
二、9.20?
10.μ= α=arctan
根据牛顿第二定律由F-μmg=ma得?
μ=
加力F′后,水平加速度不变,有?
F+F′cosα-μ(mg+F′sinα)=ma?
与上式联立得α=arctan
说明推力方向只能与水平方向成α角向下,因施推力后加速度不变,则必有F′cosα=μF′sinα.?
即得tanα=?
所以α=arctan
11.t=(M-m)v0/mg;
12.t1∶t2;F∶Ff=(t1+t2)∶t1?
三、13.因为l2被剪断瞬间,l1上的张力大小发生了变化.(1)错.因为l2被剪断的瞬间,弹簧的长度来不及发生变化,力T1的大小和方向都不能突变,(2)对.?
14.依题意,0.2 s后P离开了托盘,0.2 s时托盘支持力恰为零,此时加速度为:?
a=(F大-mg)/m ①?
(式中F大为F的最大值)此时M的加速度也为a.?
a=(kx-Mg)/M ②?
所以kx=M(g+a) ③?
原来静止时,压缩量设为x0,则:?
kx0=(m+M)g ④?
而x0-x=at2/2 ⑤?
由③、④、⑤有:at2?
即mg-Ma=0.02ak?
a=mg/(M+0.02k)=6 m/s2 ⑥?
⑥代入①:Fmax=m(a+g)=10.5(6+10)N=168 N?
F最大值为168 N.?
刚起动时F为最小,对物体与秤盘这一整体应用牛顿第二定律得?
F小+kx0-(m+M)g=(m+M)a ⑦?
④代入⑦有:Fmin=(m+M)a=72 N?
F最小值为72 N.?
15.(1)坠落物做自由落体运动的时间:h=gt2?
落地速度v0=gt?
地面人员逃离时间t′=t-0.2?
逃离速度v=?
求得t=7 s v0=70 m/s v=10.3 m/s?
(2)根据牛顿运动定律可知:(F-mg)=ma=m
求得F=5.64×106 N?
(3)震动同时产生传播,则由匀速运动知?
?
求得s=23.1 km?
版权所有:高考资源网(www.)
图1—10—5
(时间60分钟,赋分100分)
训练指要
本套试题训练和考查的重点是:进一步理解和掌握牛顿运动定律.能熟练地运用牛顿定律解题,并能解答较简单的连接体问题.第13题和第15题为创新题.第13题有利于提高学生的思维判断能力.第15题有利于提高学生的审题能力.
一、选择题(每小题5分,共40分)
1.如图1—10—1所示,悬挂于小车里的小球偏离竖直方向θ角,则小车可能的运动情况是
图1—10—1
A.向右加速运动 B.向右减速运动 C.向左加速运动 D.向左减速运动
2.如图1—10—2所示为一光滑竖直圆槽,AP、BP、CP为通过最低点P与水平面分别成30°、45°、60°角的三个光滑斜面,与圆相交于A、B、C点.若一物体由静止分别从A、B、C滑至P点所需的时间为t1,t2,t3,则
图1—10—2
A.t1<t2<t3 B.t1>t2>t3 C.t1=t2=t3 D.t1=t2<t3
3.在升降机内的地板上放一秤,一人让在秤上,用W表示升降机匀速运动时秤的示数,W1和W2分别表示升降机以大小为a的加速度加速上升和减速下降时称的示数,则
A.W2<W<W1 B.W<W1 W<W2 C.W<W1=W2 D.W>W1 W>W2
4.如图1—10—3所示,在托盘测力计的托盘内固定一个倾角为30°的光滑斜面,现将一个重4 N的物体放在斜面上,让它自由滑下,那么测力计因4 N物体的存在,而增加的读数是
图1—10—3
A.4 N B.2 N C.0 N D.3 N
5.如图1—10—4所示水平面上,质量为10 kg的物块A拴在一个被水平拉伸的弹簧一端,弹簧的另一端固定在小车上,小车静止不动,弹簧对物块的弹力大小为5 N时,物块处于静止状态,若小车以加速度a=1 m/s2沿水平地面向右加速运动时
图1—10—4
A.物块A相对小车仍静止
B.物块A受到的摩擦力将减小
C.物块A受到的摩擦力大小不变
D.物块A受到的弹力将增大
6.如图1—10—5所示,A和B的质量分别是1 kg和2 kg,弹簧和悬线的质量不计,在A上面的悬线烧断的瞬间
A.A的加速度等于3g
B.A的加速度等于g
C.B的加速度为零
D.B的加速度为g
7.(2001年上海高考试题)如图1—10—6一升降机在箱底装有若干个弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中
A.升降机的速度不断减小
B.升降机的加速度不断变大
C.先是弹力做的负功小于重力做的正功,然后是弹力做的负功大于重力做的正功
D.到最低点时,升降机加速度的值一定大于重力加速度的值
图1—10—6 图1—10—7
8.如图1—10—7所示,一根轻质弹簧上端固定,下端挂一质量为m0的平盘,盘中有一物体,质量为m.当盘静止时,弹簧的长度比其自然长度伸长了L.今向下拉盘使弹簧再伸长 ΔL后停止,然后松手放开.设弹簧总处在弹性限度以内,则刚刚松开手时盘对物体的支持力等于
A.(1+)mg B.(1+)(m+m0)g
C. mg D. (m+m0)g
二、填空题(每小题6分,共24分)
9.汽车在水平公路上做直线运动,它的功率保持不变,当汽车的速度为4 m/s时,加速度为0.4 m/s2,汽车所受阻力恒为车重的0.01倍,若取g=10 m/s2,汽车行驶的最大速度为_______ m/s.
10.已知质量为m的木块的大小为F的水平拉力作用下沿粗糙水平地面做匀加速直线运动,加速度为a,则木块与地面之间的动摩擦因数为_______.若在木块上再施加一个与水平拉力F在同一竖直平面内的推力,而不改变木块的加速度的大小和方向,则此推力与水平拉力F的夹角为_______.
11.总质量为M的热气球由于故障在空中以速度v0匀速下降.为了阻止继续下降,在t=0时刻,从热气球中释放了一个质量为m的沙袋.不计空气阻力,当t=________时,热气球停止下降,这时沙袋的速度为________.
12.一辆小车在水平恒力F作用下,由静止开始在水平面上匀加速运动t1 s后撤去F,小车再经过t2 s停下.则小车加速阶段的位移s1与减速阶段的位移s2之比s1∶s2=______;小车牵引力F与所受的摩擦力Ff之比F∶Ff=______.
三、计算题(共36分)
13.(12分)如图1—10—8所示,一质量为m的物体系于长度分别为l1、l2的两根细线上,l1的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态.现将l2线剪断,求剪断瞬时物体的加速度.
图1—10—8
(1)下面是某同学对该题的一种解法:
解:设l1线上拉力为T1,l2线上拉力为T2,重力为mg,物体在三力作用下保持平衡
T1cosθ=mg,T1sinθ=T2,T2=mgtanθ
剪断线的瞬间,T2突然消失,物体即在T2反方向获得加速度.因为mgtanθ=ma,所以加速度a=gtanθ,方向与T2反方向.
你认为这个结果正确吗 请对该解法作出评价并说明理由.
(2)若将图1—10—8中的细线l1改为长度相同、质量不计的轻弹簧,如图1—10—9所示,其他条件不变,求解的步骤和结果与(1)完全相同,即a=gtanθ,你认为这个结果正确吗 请说明理由.
图1—10—9
14.(12分)一弹簧秤的秤盘质量M=1.5 kg,盘内放一物体P,物体P的质量m=10.5 kg,弹簧质量不计,其劲度系数为k=800N/m,系统处于静止状态,如图1—10—10所示.现给P施加一个竖直向上的力F,使P从静止开始向上做匀加速运动,已知在头0.2 s内F是变力,在0.2 s以后是恒力.求F的最小值和最大值各是多少 (g=10 m/s2)
图1—10—10
15.(12分)2001年9月11日,美国遭受了历史上规模最大、损失最为惨重的恐怖主义袭击,恐怖分子劫持客机分别撞击了纽约的“世贸大楼”和华盛顿的“五角大楼”.其中一架客机拦腰撞到世贸大楼的南部塔楼第60层地方,并引起巨大爆炸,大约1 h后,南部塔楼部分轰然倒塌(高约245 m),灰尘和残骸四处飞溅,300多名救援警察和消防人员没来得及逃生.
我们不妨设置一个情境:当处于倒塌部分正下方的地面人员,看到一块质量约为4× 103 kg的楼墙块竖直倒下的同时到作出反应开始逃离需0.2 s的时间,逃离的安全区域为离大厦100 m外(实际的安全区要更远).设该坠落块与地面作用时间为0.05 s,不计空气阻力,g取10 m/s2.求:
(1)地面人员要逃离大厦到安全区至少要以多大速度奔跑?(忽略人的加速时间,百米短跑世界记录为9″79)
(2)该坠落块对地产生的平均作用力多大?
(3)由于爆炸引起地表震动,设产生的纵波的传播速率vp=9.1 km/s,横波的传播速率vs=3.1 km/s,设在某处的地震勘测中心记录到两种不同震感之间的时间间隔Δt0=5 s,那么观测记录者与震源之间的距离s为多少千米?
参考答案
一、1.AD 2.C 3.BC 4.D 5.AC 6.AC 7.CD?
8.A 以盘和重物为一个整体加以隔离,平衡时?
kL=(m+m0)g,k=.?
用手向下拉,弹簧共伸长L+ΔL,弹力F=k(L+ΔL)?
手的瞬时,根据牛顿第二定律F-(m+m0)g=(m+m0)α.把F值代入得
(L+ΔL)-(m+m0)g=(m+m0)a?
a=g,方向向上.?
隔离盘中物体,设盘对物体的支持力为N,由牛顿第二定律N-mg=ma?
故N=mg+ma=mg+mg=(1+)mg,向上.?
二、9.20?
10.μ= α=arctan
根据牛顿第二定律由F-μmg=ma得?
μ=
加力F′后,水平加速度不变,有?
F+F′cosα-μ(mg+F′sinα)=ma?
与上式联立得α=arctan
说明推力方向只能与水平方向成α角向下,因施推力后加速度不变,则必有F′cosα=μF′sinα.?
即得tanα=?
所以α=arctan
11.t=(M-m)v0/mg;
12.t1∶t2;F∶Ff=(t1+t2)∶t1?
三、13.因为l2被剪断瞬间,l1上的张力大小发生了变化.(1)错.因为l2被剪断的瞬间,弹簧的长度来不及发生变化,力T1的大小和方向都不能突变,(2)对.?
14.依题意,0.2 s后P离开了托盘,0.2 s时托盘支持力恰为零,此时加速度为:?
a=(F大-mg)/m ①?
(式中F大为F的最大值)此时M的加速度也为a.?
a=(kx-Mg)/M ②?
所以kx=M(g+a) ③?
原来静止时,压缩量设为x0,则:?
kx0=(m+M)g ④?
而x0-x=at2/2 ⑤?
由③、④、⑤有:at2?
即mg-Ma=0.02ak?
a=mg/(M+0.02k)=6 m/s2 ⑥?
⑥代入①:Fmax=m(a+g)=10.5(6+10)N=168 N?
F最大值为168 N.?
刚起动时F为最小,对物体与秤盘这一整体应用牛顿第二定律得?
F小+kx0-(m+M)g=(m+M)a ⑦?
④代入⑦有:Fmin=(m+M)a=72 N?
F最小值为72 N.?
15.(1)坠落物做自由落体运动的时间:h=gt2?
落地速度v0=gt?
地面人员逃离时间t′=t-0.2?
逃离速度v=?
求得t=7 s v0=70 m/s v=10.3 m/s?
(2)根据牛顿运动定律可知:(F-mg)=ma=m
求得F=5.64×106 N?
(3)震动同时产生传播,则由匀速运动知?
?
求得s=23.1 km?
版权所有:高考资源网(www.)
图1—10—5
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
