第一节 分类加法计数原理与分步乘法计数原理课件(20张ppt)
文档属性
| 名称 | 第一节 分类加法计数原理与分步乘法计数原理课件(20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-26 00:00:00 | ||
图片预览








文档简介
课件20张PPT。高中数学人教版选修2-3 第一章第1节
《分类加法计数原理与分步乘法计数原理》(1)创设情境:某城市选择个性化牌照的规则是:①第一位必须选择英文字母,后四位中必须选择一位为英文字母,其余三位为阿拉伯数字;②英文字母不得选用I、O、Q;
这样的个性化牌照的容量是多少?通过引入生活中的实例体现数学来源于生活并服务生活的特点,激发学生学习数学的兴趣理解分类加法与分步乘法计数原理,初步学会“分类”与“分步”,能用这两个计数原理解决实际问题培养学生用观察、归纳、类比的方法发现事物的规律,引导学生树立分类讨论的思想,提高逻辑思维能力重点:归纳出分类加法与分步乘法计数原理,并能解决简单的计数问题。
难点:正确理解“完成一件事”的含义,根据实际问题的特征正确区分“分类”或“分步”。
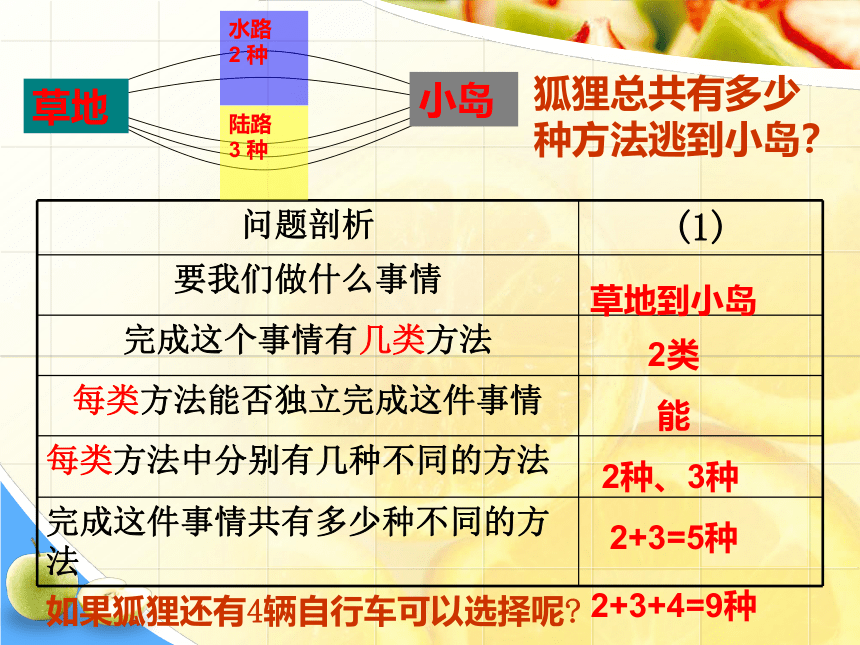
重点难点 狐狸想从草地逃到小岛,可以走水路,也可以走陆路,走水路有2艘船,走陆路有3辆车,问:乘坐这些交通工具,共有多少种不同的方法,可以从草地逃到小岛?狐狸总共有多少种方法逃到小岛?草地到小岛2类能2种、3种2+3=5种水路
2 种陆路
3 种如果狐狸还有4辆自行车可以选择呢?2+3+4=9种草地小岛如果狐狸还有m3辆自行车可以选择呢?N=m1+m2+m3 如果狐狸从草地到小岛的交通工具有n类,第一类m1种,第二类有m2种,...,第n类有mn种不同的方法,那么狐狸到安全地有多少种不同的方法?N=m1+m2+…+mn狐狸总共有多少种方法逃到小岛?水 路
m1 种陆 路
m2种草地小岛N=m1+m2一、分类加法计数原理 完成一件事,有两类方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有
1)首先要根据具体的问题确定一个分类标准,在分类标准下进行分类,然后对每类方案中的方法计数.说明N= m+ n种不同的方法.
2)各类办法之间相互独立,用每类中任何一种方法都能独立的完成这件事。3)要计算方法种数,只需将各类方案中的方法数相加,因此分类计数原理又称加法原理从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有4 班, 汽车有2班,轮船有3班。那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法?分析: 从甲地到乙地有3类方法,
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以 从甲地到乙地共有 4 + 2 + 3 = 9 种方法。 学以致用 狐狸有一共有多少种不同的方法,可以从草地逃回到自己的家(安全地)?草地到安全地2步不能5种、2种5×2=10种a1a2
a3a4 a5b1
b2别墅如果狐狸还有4种方法到别墅压惊呢?5×2×4=40种二、分步乘法计数原理 完成一件事,需要分成两个步骤。做第1步有m种不同的方法,做第2步有n种不同的方法,那么 完成这件事共有
1)首先要根据具体问题的特点确定一个分步的标准,然后对每步方法计数.说明N= m×n种不同的方法
2)各个步骤相互依存,只有各个步骤都完成了,这件事才算完成,3)将各个步骤的方法数相乘得到完成这件事的方法总数,又称乘法原理 分析: 从A村经 B村去C村有2步,
第一步, 由A村去B村有3种方法,
第二步, 由B村去C村有2种方法,
所以 从A村经 B村去C村共有 3 ×2 = 6 种不同的方法。学以致用书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书. (1)从书架中取1本书,有多少种不同取法? (2)从书架第1,2,3层各取1本书,有多少种不同取法?
解题关键:从总体上看做这件事情是“分类完成”,还是“分步完成”.再根据其对应的计数原理计算.思考分组讨论知识升华相同点区别分类,相加分步,相乘每类办法都能独立完
成这件事情。任何一步都不能独立完成,
只有每个步骤完成了,才
能完成这件事情。
类类独立,不重不漏步步相依,缺一不可分类计数与分步计数原理的区别和联系:都是用来计算完成一件事情不同的方法种数的问题。归纳如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路可以走,从丙地到丁地有2条路。从甲地到丁地共有多少种不同地走法?N1=2×3=6N2=4×2=8N= N1+N2 =14思考AB如图,该电路从A到B共有多少条不同的线路可通电?思考能力提升:1.将3封不同的信投到4个不同的邮箱,则不同的投法的种数为( ) A. 7 B. 12 C. 81 D. 64D2.在一次运动会上有四项比赛的冠军在甲、乙、丙三人中产生,那么不同的夺冠情况的种数为( ) A. 6 B. 24 C. 81 D. 64C课本第6页练习1.2
习题A组1.2.3,B组1.2作业
《分类加法计数原理与分步乘法计数原理》(1)创设情境:某城市选择个性化牌照的规则是:①第一位必须选择英文字母,后四位中必须选择一位为英文字母,其余三位为阿拉伯数字;②英文字母不得选用I、O、Q;
这样的个性化牌照的容量是多少?通过引入生活中的实例体现数学来源于生活并服务生活的特点,激发学生学习数学的兴趣理解分类加法与分步乘法计数原理,初步学会“分类”与“分步”,能用这两个计数原理解决实际问题培养学生用观察、归纳、类比的方法发现事物的规律,引导学生树立分类讨论的思想,提高逻辑思维能力重点:归纳出分类加法与分步乘法计数原理,并能解决简单的计数问题。
难点:正确理解“完成一件事”的含义,根据实际问题的特征正确区分“分类”或“分步”。
重点难点 狐狸想从草地逃到小岛,可以走水路,也可以走陆路,走水路有2艘船,走陆路有3辆车,问:乘坐这些交通工具,共有多少种不同的方法,可以从草地逃到小岛?狐狸总共有多少种方法逃到小岛?草地到小岛2类能2种、3种2+3=5种水路
2 种陆路
3 种如果狐狸还有4辆自行车可以选择呢?2+3+4=9种草地小岛如果狐狸还有m3辆自行车可以选择呢?N=m1+m2+m3 如果狐狸从草地到小岛的交通工具有n类,第一类m1种,第二类有m2种,...,第n类有mn种不同的方法,那么狐狸到安全地有多少种不同的方法?N=m1+m2+…+mn狐狸总共有多少种方法逃到小岛?水 路
m1 种陆 路
m2种草地小岛N=m1+m2一、分类加法计数原理 完成一件事,有两类方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有
1)首先要根据具体的问题确定一个分类标准,在分类标准下进行分类,然后对每类方案中的方法计数.说明N= m+ n种不同的方法.
2)各类办法之间相互独立,用每类中任何一种方法都能独立的完成这件事。3)要计算方法种数,只需将各类方案中的方法数相加,因此分类计数原理又称加法原理从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有4 班, 汽车有2班,轮船有3班。那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法?分析: 从甲地到乙地有3类方法,
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以 从甲地到乙地共有 4 + 2 + 3 = 9 种方法。 学以致用 狐狸有一共有多少种不同的方法,可以从草地逃回到自己的家(安全地)?草地到安全地2步不能5种、2种5×2=10种a1a2
a3a4 a5b1
b2别墅如果狐狸还有4种方法到别墅压惊呢?5×2×4=40种二、分步乘法计数原理 完成一件事,需要分成两个步骤。做第1步有m种不同的方法,做第2步有n种不同的方法,那么 完成这件事共有
1)首先要根据具体问题的特点确定一个分步的标准,然后对每步方法计数.说明N= m×n种不同的方法
2)各个步骤相互依存,只有各个步骤都完成了,这件事才算完成,3)将各个步骤的方法数相乘得到完成这件事的方法总数,又称乘法原理 分析: 从A村经 B村去C村有2步,
第一步, 由A村去B村有3种方法,
第二步, 由B村去C村有2种方法,
所以 从A村经 B村去C村共有 3 ×2 = 6 种不同的方法。学以致用书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书. (1)从书架中取1本书,有多少种不同取法? (2)从书架第1,2,3层各取1本书,有多少种不同取法?
解题关键:从总体上看做这件事情是“分类完成”,还是“分步完成”.再根据其对应的计数原理计算.思考分组讨论知识升华相同点区别分类,相加分步,相乘每类办法都能独立完
成这件事情。任何一步都不能独立完成,
只有每个步骤完成了,才
能完成这件事情。
类类独立,不重不漏步步相依,缺一不可分类计数与分步计数原理的区别和联系:都是用来计算完成一件事情不同的方法种数的问题。归纳如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路可以走,从丙地到丁地有2条路。从甲地到丁地共有多少种不同地走法?N1=2×3=6N2=4×2=8N= N1+N2 =14思考AB如图,该电路从A到B共有多少条不同的线路可通电?思考能力提升:1.将3封不同的信投到4个不同的邮箱,则不同的投法的种数为( ) A. 7 B. 12 C. 81 D. 64D2.在一次运动会上有四项比赛的冠军在甲、乙、丙三人中产生,那么不同的夺冠情况的种数为( ) A. 6 B. 24 C. 81 D. 64C课本第6页练习1.2
习题A组1.2.3,B组1.2作业
