古埃及的数学

课件42张PPT。 高中数学选修3-1 数学史选讲 第一讲 早期的算术与几何 一、古埃及的数学埃及金字塔人面狮身像荷鲁斯之眼古典希腊
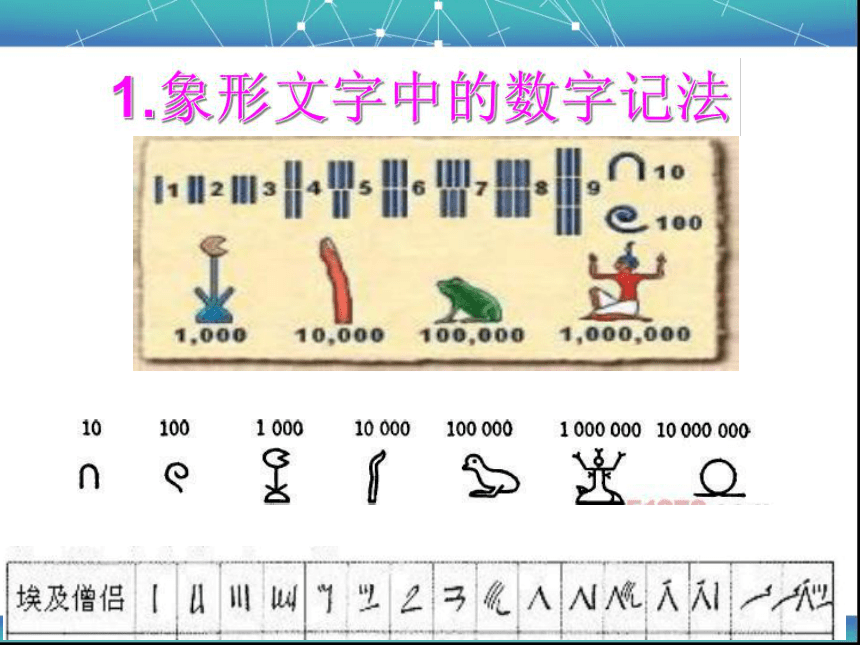
数学僧侣文24认一认1238认一认999999认一认写一写用象形文写出下列数字：
（1）545
（2）4857 古埃及计数的特点：1.采用十进制；2.没有位值制；3.要创设很多新符号，计数较麻烦。2.纸草书上的数学《莱因德纸草书》﹝Rhind Papyrus﹞是公元前1650年左右的埃及数学著作，属于世界上最古老的数学著作之一。作者是书记官阿默斯，共有84个问题。公元1858年由英国的埃及学者莱因德﹝A. H. Rhind﹞购得，故得名。现藏于伦敦大英博物馆。该纸草书全长544厘米，宽33厘米。莱茵德纸草书记载着古埃及数学的另一部古典书籍是莫斯科纸草书，此书是由俄罗斯收藏者于1893年获得的．约20年后，即1912年转藏于莫斯科图书馆．这部纸草书长约550厘米、宽8厘米，共记载着25个问题．莫斯科纸草书纸草书上的数学纸草书上的数学准确的计算，阐明一切黑暗的、秘密存在的事物指南。从“莱茵德纸草书”、“莫斯科纸草书”等可看出，古埃及人的数学知识包括算术、代数和几何三个方面。纸草书上的数学 古埃及的分数纸草书上的数学 单分数古埃及的单分数有一种观点认为，单分数就是从实际问题中产生的。
问题：将2个面包平均分给5个人，如何分？一个古老的传说: 老人弥留之际，将家中11匹马分给3个儿子，老大1/2，老二1/4，老三1/6。该怎么分呢？二分之一是5匹半马，总不能把马杀了吧。 正在无奈之际，邻居把自己家的马牵来，老大二分之一，牵走了6匹;老二四分之一，牵走了3匹;老三六分之一，牵走了2匹。一共11匹，分完后，邻居把自己的马牵了回去。古埃及的记数制与算术 象征荷鲁斯之眼的象形文字的每一个元素分别表示1/2、1/4、1/8、1/16、1/32、1/64，将它们组合起来可以表示分母为64的任何分数。
几何级数的雏形 埃及分数是无穷级数的一种特殊表现形式，无穷级数的一个重要应用就是对函数值的逼近。所以用埃及分数对函数值尤其对无理数估值自古以来就受到广泛关注，例如：
古埃及的加减法运算 埃及的加法运算主要用叠加法，做通常加减法时，他们只是靠添上或划掉一些记号，以求得最后结果。10+5=15古埃及的乘除运算（倍乘法）
计算：3x6=？乘法.flv古埃及的算术运算计算：25×18=？古埃及的算术运算计算：27×3177÷14古埃及的代数问题 在埃及纸草书中有求一个未知量问题的解法，这个问题大体上相当于今日的一元一次方程，不过用的方法纯粹是算术的 。
例如：一个量，加上自身的七分之一 等于19.
暂定前提法3.几何学的诞生尼罗河泛滥.mp4希腊历史学家希罗多德说：
埃及是受尼罗河恩施的。埃及法老（拉美西斯二世，约公元前１３００年）把土地分成大小相同的小正方形，然后分给每一个埃及人，同时，制定年税的支付并以此作为国家收入的来源。如果一个人的土地被河水冲走，他可以找法老申报所发生的事，然后法老会派人去调查并测量减少的土地数量。这样以后就按剩下土地的面积来缴税。“我想，正是有了这样的做法，埃及才第一次有了几何学。”几何学的诞生－－希罗多德《历史》古埃及的几何学（geo metry） 土地的测量促使几何学的兴起，从事土地测量的人员叫“拉绳者”，“拉绳者”就是当时的几何学家。 埃及人把几何看作实用工具，用来解决有关面积、体积及其他几何性质的问题。 古埃及的几何学埃及人对圆面积的计算好得惊人，用的公式是A=(8d/9)2 ，其中d是直径，这就等于π为3.1605。 以埃及的大金字塔为例，它的高度（481.3949英尺）和周长（3023.16英尺）之间的比率，恰好
等于一个圆圈的半径和圆周之间的比率，即2π。
如果将这座金字塔的高度乘以2π（如同我们根据一个圆圈的半径计算它的圆周），我们就能够精确算出金字塔的周长：481.3949×2×3.14＝3023.1 6。相反地，如果我们将这座金字塔的周长除以2π，也同样可以算出它的高度。 3023.16/2/3.14＝481.3949。?
这样精确的数学关联，几乎不可能出于单纯的巧合。因此，我们不得不承认，埃及大金字塔的设计师确实了解π的原理，刻意将它的数值应用到金宇塔的营建上。 古埃及的几何学在埃德富(Edfu)一个庙宇的墙上刻有一个捐献给庙宇的田地表，这些田地一般有四边，今将其记为a、b、c、d，其中a与b以及c与d是两批相对的边，铭文给出的这些田地的面积是 古埃及的几何学毕达哥拉斯定理（勾股定理）我们也不知道埃及人是否认识到Pythagoras定理，我们知道他们有拉绳人（测量员），所传他们在绳上打结，把全长分成长度各为3比4比5的三段，然后用来形成直角三角形。 古埃及的几何学古埃及的体积计算：
埃及几何里最了不起的一个法则是计算截棱锥体的体积公式，椎体的底是正方形这个公式用现代的记号是：古埃及的几何学莫斯科纸草书记载：“若有人告诉你说，有截棱锥，高为6，底为4，顶为2。你就要取这4的平方，得结果16。你要把它加倍，得结果8。你要取2的平方，得4。你要把16、8和4加起来，得28。你要取6的三分之一，得2。你要取28的两倍，得56。

古埃及数学与现代数学（2）乘法的倍乘------二进制
（1）荷鲁斯之眼------数列（几何级数） （3）土地测量-----毕达哥拉斯定理（勾股定 理） ， 圆周率，台体体积的计算最古老的也是最现代的。埃及人是惊人的创造者，他们创造数学的能力是难以置信的。对我们来说，他们揭示了几何和数学的威力，实现了令人兴奋的数学发现第一步。
埃及人是惊人的创造者，他们创造数学的能力是难以置信的。对我们来说，他们揭示了几何和数学的威力，实现了令人兴奋的数学发现第一步。