数学五年级上人教版6组合图形的面积教学设计
文档属性
| 名称 | 数学五年级上人教版6组合图形的面积教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 97.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-27 00:00:00 | ||
图片预览


文档简介
第四课时 组合图形的面积
一、学习目标
(一)学习内容
《义务教育教科书数学》(人教版)五年级上册第99页例题4,是学生在学习了长方形、正方形、平行四边形、三角形和梯形面积后进行教学的。
(二)核心能力
在运用转化的思想,将组合图形面积转化为计算简单图形面积的过程中,进一步发展空间观念。
(三)学习目标
1.结合生活实例认识组合图形,自主地能够将组合图形分解成已学过的平面图形。
2.结合具体情境,通过小组合作交流掌握“割”、“补”等方法来计算组合图形的面积,发展空间观念。
3.运用所学到的知识和方法,根据问题和具体数据选择适当方法解决实际问题。
(四)学习重点
探索并掌握组合图形的面积计算方法。
(五)学习难点
理解并掌握组合图形的组合及分解方法。
(六)配套资源
实施资源:《组合图形的面积》教学课件
二、学习设计
(一)课前设计
1.复习任务
(1)整理已经学过了哪些平面图形面积的计算,写出它们的面积公式。
(2)分别编一道这些图形在生活中应用的题目,并解答。
【设计意图:复习已有的平面图形面积计算公式,可以帮助激活旧知在接下来的教学中,较容易的认识组合图形的组成及其之后的计算。】
(二)课堂设计
1.导入
(1)认识组合图形
交流复习任务。
师:像这些比较简单的图形,我们把它叫做简单图形。而生活中可不是只有简单图形,还有着更复杂的图形,他们叫做组合图形。同学们请看大屏幕。这三个图形就是组合图形。我们把由几个简单图形组合而成的图形叫组合图形。
(板书:组合图形)这节课我们就一起来探究组合图形的有关知识。
师:认真观察这三个图形,同桌之间说一说它们分别是由哪些简单图形组成的?
预设:第一个三角形和长方形。追问第二个呢?
三角形、两个梯形和长方形。最后一个呢?
三角形和长方形。
【设计意图:通过出示简单的组合图形分隔情况,为接下来的正式教学打下铺垫,利于学生更易掌握组合图形面积计算方法。考察目标1】
师:同学们,开动脑筋想想:生活中哪些地方还有组合图形?你能给大家举个例子吗?
预设:远处的楼房、窗户框等等。
(2)导入新课
师:同学们真棒呀!知道生活中存在着很多美丽的组合图形。老师这里也收集了一些美丽的图片。例如:房子的屋顶、告示牌和队旗。(依次出示PPT)
师:生活中存在着很多美丽的组合图形,那如果老师想知道这些组合图形有多大,实际上是求什么?(板书:的面积)
2.问题探究
(1)自主探索,尝试计算
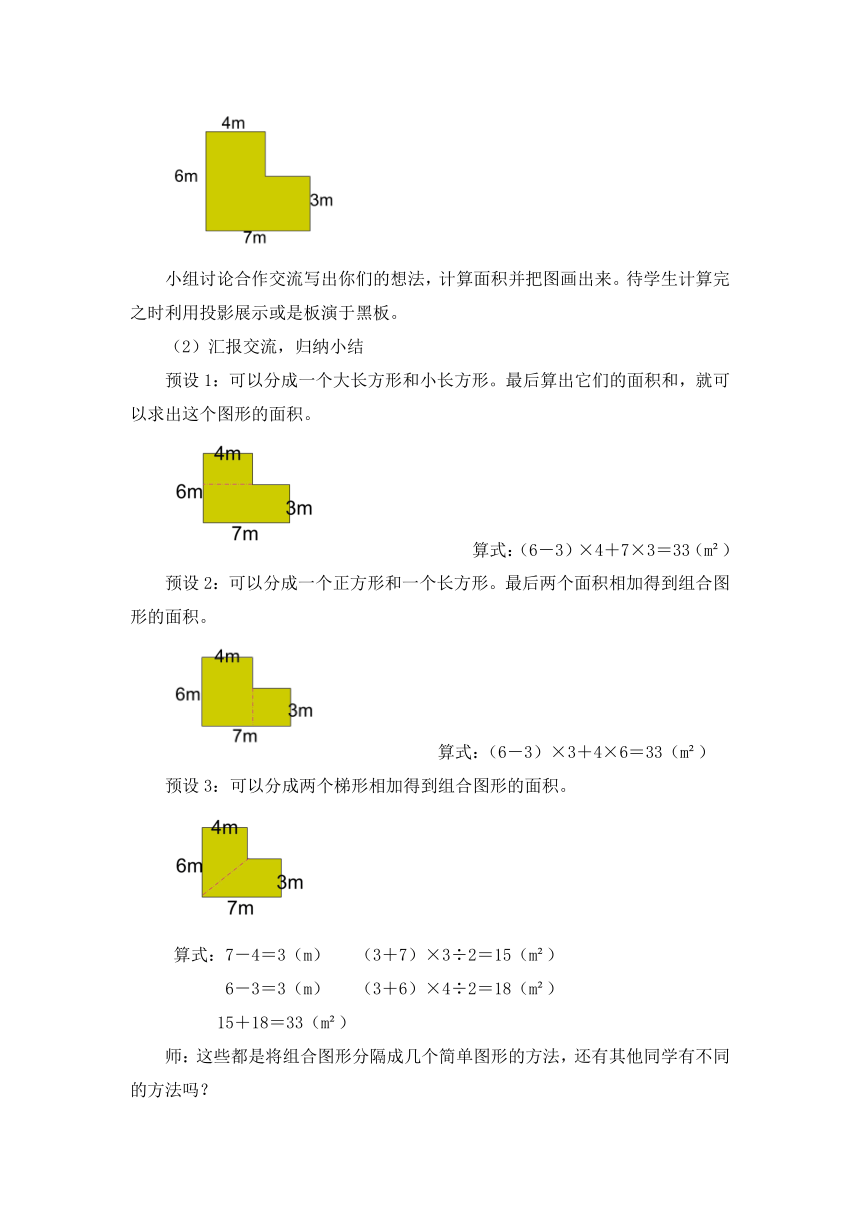
师:小明也遇到了相同的困惑,咱们一起来帮帮他。最近小明家搬了新家,需要铺木地板(平面图如下)。请大家帮他算一算他家至少要买多少平米的木地板?(PPT展示)
小组讨论合作交流写出你们的想法,计算面积并把图画出来。待学生计算完之时利用投影展示或是板演于黑板。
(2)汇报交流,归纳小结
预设1:可以分成一个大长方形和小长方形。最后算出它们的面积和,就可以求出这个图形的面积。
算式:(6-3)×4+7×3=33(m2)
预设2:可以分成一个正方形和一个长方形。最后两个面积相加得到组合图形的面积。
算式:(6-3)×3+4×6=33(m2)
预设3:可以分成两个梯形相加得到组合图形的面积。
算式:7-4=3(m) (3+7)×3÷2=15(m2)
6-3=3(m) (3+6)×4÷2=18(m2)
15+18=33(m2)
师:这些都是将组合图形分隔成几个简单图形的方法,还有其他同学有不同的方法吗?
预设:把这个组合图形“补成”一个大的长方形,最后再减去补的那一部分。
算式:7×6-(6-3)×(7-4)=33(m2)
师:我们一起来总结一下我们所用到的方法,我们给前三个把前三个将组合图形分隔的方法叫做分割法,把最后一种添上一块,再减去的方法七个名字叫做添补法。(PPT演示)
师:其实小明自己也有一种分割的方法,大家来评判一下好不好。(PPT演示)
预设:不好,分成了好多块,计算麻烦。
总结:所以在计算组合图形的时候分割或是添补都要简单便捷。
【设计意图:结合具体情境,在小组讨论中激活学生的思维,创造出多种多样的计算方法。教师最后进行总结,提示应尽量简单便捷的计算。在碰撞和“找错误”中完成知识的学习。考察目标1、2】
(3)灵活应用,巩固新知
师:刚才同学们帮小明算了客厅的面积,下图是房子侧面墙的形状?你能算出它的面积吗?你能想出几种方法?小组合作,讨论完成。(PPT展示)
预设1:用分割法把这个组合图形一分为二,一个是正方形,另一个是三角再分别算出正方形和三角形的面积,最后算出它们的面积和,就可以求出这个图形的面积。(PPT出示第一种方法)
5×5=25(m2) 5×2÷2=5(m2)
25+5=30(m2)
预设2:把这个图形分成两个梯形,这两个梯形面积是相等的,所以只要求出一个梯形的面积再乘以2,就得到这个组合图形的面积。(PPT出示第二种方法)
(5+7)×2.5÷2×2=30(m2)
预设3:用割补法先把这个图形补上两个三角形,看作一个长方形,先算出长方的面积后,再减去两个小三角形的面积。(PPT出示第三种方法)
5×(5+2)-2.5×2÷2×2=30(m2)
【设计意图:通过课本例题巩固本节课所学到的重点和难点。进一步强化计算组合图形面积用到的分割法和割补法。考察目标2、3】
3.课堂总结
(1)通过这一节课的学习,同学们有什么收获?
(2)通过这节课的学习你有哪些收获,我们能怎样运用今天的知识呢?
三、课时作业
1.一张长方形的铁板,从长边的中点到两个宽边的中点分别连一条线,沿这两条线剪下来两个角。求剩下图形的面积是多少?
答案:28÷2=14cm 20÷2=10cm 28×20-14×10÷2×2=420cm2
答:剩下的图形面积是420cm2。
解析:本题根据图片已有的连线,运用割补法求出阴影部分的面积。【考查目标2】
2.一块铁板的形状如下图。在这块铁板的两面涂上油漆,涂油漆的面积是多少?(单位:分米)
答案:4+2+2=8 10-8=2 (4+8)×2÷2=12 8×8=64
64+12=76
答:涂油漆的面积是76平方分米。
解析:本题根据图片运用割补法将图形分成一个大正方形和一个小梯形,运用已有的数据,首先求出梯形的下底,和正方形的边长,从而求得面积。【考查目标2、3】
3.小丽家装修需要30块木板,木板的形状如下图。一块木板的面积是多少?(用两种方法计算)
答案:(1)60-30=30cm 48×30=1440cm2
(48+72)×30÷2=1800cm2 1440+1800=3240cm2
(2)72-48=24cm (30+60)×24÷2=1080cm2
60×72=4320cm2 4320-1080=3240cm2
答:一块木板面积是3240cm2。
解析:本题根据图片运用割补法将图形分成一个长方形和一个小梯形两者相加。第二种运用添补法补出一个大长方形和一个小梯形,两者相减从而求得面积。【考查目标2、3】
一、学习目标
(一)学习内容
《义务教育教科书数学》(人教版)五年级上册第99页例题4,是学生在学习了长方形、正方形、平行四边形、三角形和梯形面积后进行教学的。
(二)核心能力
在运用转化的思想,将组合图形面积转化为计算简单图形面积的过程中,进一步发展空间观念。
(三)学习目标
1.结合生活实例认识组合图形,自主地能够将组合图形分解成已学过的平面图形。
2.结合具体情境,通过小组合作交流掌握“割”、“补”等方法来计算组合图形的面积,发展空间观念。
3.运用所学到的知识和方法,根据问题和具体数据选择适当方法解决实际问题。
(四)学习重点
探索并掌握组合图形的面积计算方法。
(五)学习难点
理解并掌握组合图形的组合及分解方法。
(六)配套资源
实施资源:《组合图形的面积》教学课件
二、学习设计
(一)课前设计
1.复习任务
(1)整理已经学过了哪些平面图形面积的计算,写出它们的面积公式。
(2)分别编一道这些图形在生活中应用的题目,并解答。
【设计意图:复习已有的平面图形面积计算公式,可以帮助激活旧知在接下来的教学中,较容易的认识组合图形的组成及其之后的计算。】
(二)课堂设计
1.导入
(1)认识组合图形
交流复习任务。
师:像这些比较简单的图形,我们把它叫做简单图形。而生活中可不是只有简单图形,还有着更复杂的图形,他们叫做组合图形。同学们请看大屏幕。这三个图形就是组合图形。我们把由几个简单图形组合而成的图形叫组合图形。
(板书:组合图形)这节课我们就一起来探究组合图形的有关知识。
师:认真观察这三个图形,同桌之间说一说它们分别是由哪些简单图形组成的?
预设:第一个三角形和长方形。追问第二个呢?
三角形、两个梯形和长方形。最后一个呢?
三角形和长方形。
【设计意图:通过出示简单的组合图形分隔情况,为接下来的正式教学打下铺垫,利于学生更易掌握组合图形面积计算方法。考察目标1】
师:同学们,开动脑筋想想:生活中哪些地方还有组合图形?你能给大家举个例子吗?
预设:远处的楼房、窗户框等等。
(2)导入新课
师:同学们真棒呀!知道生活中存在着很多美丽的组合图形。老师这里也收集了一些美丽的图片。例如:房子的屋顶、告示牌和队旗。(依次出示PPT)
师:生活中存在着很多美丽的组合图形,那如果老师想知道这些组合图形有多大,实际上是求什么?(板书:的面积)
2.问题探究
(1)自主探索,尝试计算
师:小明也遇到了相同的困惑,咱们一起来帮帮他。最近小明家搬了新家,需要铺木地板(平面图如下)。请大家帮他算一算他家至少要买多少平米的木地板?(PPT展示)
小组讨论合作交流写出你们的想法,计算面积并把图画出来。待学生计算完之时利用投影展示或是板演于黑板。
(2)汇报交流,归纳小结
预设1:可以分成一个大长方形和小长方形。最后算出它们的面积和,就可以求出这个图形的面积。
算式:(6-3)×4+7×3=33(m2)
预设2:可以分成一个正方形和一个长方形。最后两个面积相加得到组合图形的面积。
算式:(6-3)×3+4×6=33(m2)
预设3:可以分成两个梯形相加得到组合图形的面积。
算式:7-4=3(m) (3+7)×3÷2=15(m2)
6-3=3(m) (3+6)×4÷2=18(m2)
15+18=33(m2)
师:这些都是将组合图形分隔成几个简单图形的方法,还有其他同学有不同的方法吗?
预设:把这个组合图形“补成”一个大的长方形,最后再减去补的那一部分。
算式:7×6-(6-3)×(7-4)=33(m2)
师:我们一起来总结一下我们所用到的方法,我们给前三个把前三个将组合图形分隔的方法叫做分割法,把最后一种添上一块,再减去的方法七个名字叫做添补法。(PPT演示)
师:其实小明自己也有一种分割的方法,大家来评判一下好不好。(PPT演示)
预设:不好,分成了好多块,计算麻烦。
总结:所以在计算组合图形的时候分割或是添补都要简单便捷。
【设计意图:结合具体情境,在小组讨论中激活学生的思维,创造出多种多样的计算方法。教师最后进行总结,提示应尽量简单便捷的计算。在碰撞和“找错误”中完成知识的学习。考察目标1、2】
(3)灵活应用,巩固新知
师:刚才同学们帮小明算了客厅的面积,下图是房子侧面墙的形状?你能算出它的面积吗?你能想出几种方法?小组合作,讨论完成。(PPT展示)
预设1:用分割法把这个组合图形一分为二,一个是正方形,另一个是三角再分别算出正方形和三角形的面积,最后算出它们的面积和,就可以求出这个图形的面积。(PPT出示第一种方法)
5×5=25(m2) 5×2÷2=5(m2)
25+5=30(m2)
预设2:把这个图形分成两个梯形,这两个梯形面积是相等的,所以只要求出一个梯形的面积再乘以2,就得到这个组合图形的面积。(PPT出示第二种方法)
(5+7)×2.5÷2×2=30(m2)
预设3:用割补法先把这个图形补上两个三角形,看作一个长方形,先算出长方的面积后,再减去两个小三角形的面积。(PPT出示第三种方法)
5×(5+2)-2.5×2÷2×2=30(m2)
【设计意图:通过课本例题巩固本节课所学到的重点和难点。进一步强化计算组合图形面积用到的分割法和割补法。考察目标2、3】
3.课堂总结
(1)通过这一节课的学习,同学们有什么收获?
(2)通过这节课的学习你有哪些收获,我们能怎样运用今天的知识呢?
三、课时作业
1.一张长方形的铁板,从长边的中点到两个宽边的中点分别连一条线,沿这两条线剪下来两个角。求剩下图形的面积是多少?
答案:28÷2=14cm 20÷2=10cm 28×20-14×10÷2×2=420cm2
答:剩下的图形面积是420cm2。
解析:本题根据图片已有的连线,运用割补法求出阴影部分的面积。【考查目标2】
2.一块铁板的形状如下图。在这块铁板的两面涂上油漆,涂油漆的面积是多少?(单位:分米)
答案:4+2+2=8 10-8=2 (4+8)×2÷2=12 8×8=64
64+12=76
答:涂油漆的面积是76平方分米。
解析:本题根据图片运用割补法将图形分成一个大正方形和一个小梯形,运用已有的数据,首先求出梯形的下底,和正方形的边长,从而求得面积。【考查目标2、3】
3.小丽家装修需要30块木板,木板的形状如下图。一块木板的面积是多少?(用两种方法计算)
答案:(1)60-30=30cm 48×30=1440cm2
(48+72)×30÷2=1800cm2 1440+1800=3240cm2
(2)72-48=24cm (30+60)×24÷2=1080cm2
60×72=4320cm2 4320-1080=3240cm2
答:一块木板面积是3240cm2。
解析:本题根据图片运用割补法将图形分成一个长方形和一个小梯形两者相加。第二种运用添补法补出一个大长方形和一个小梯形,两者相减从而求得面积。【考查目标2、3】
