数学五年级上人教版6多边形的面积复习课教学设计
文档属性
| 名称 | 数学五年级上人教版6多边形的面积复习课教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 255.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-27 20:33:52 | ||
图片预览

文档简介
单元复习 多边形的面积
一、复习内容
《义务教育教科书数学》(人教2014版)五年级上册第86~105页。
二、复习目标
1.通过小组合作,回顾梳理本单元知识,能用思维导图清晰的整理单元知识网络,并熟练运用本单元知识解决实际问题。
2.经历单元复习过程,熟练掌握单元知识的同时,再次感受合作学习的重要性以及转化思想在数学学习中的重要性,培养良好的数学学习兴趣。
三、复习重、难点
平行四边形、三角形、梯形面积公式的推导过程;灵活运用平行四边形、三角形、梯形的面积公式解决问题。
四、配套资源
《多边形的面积复习课》教学课件
五、复习设计
(一)课前作业
复习课本P86——P105,思考本单元都学习了哪些内容?你认为学习本单元的关键在哪里?对本单元知识进行知识梳理,形成知识导图。
【设计意图:学生课前自主复习,培养自主复习的意识,提高自主复习并绘制思维导图的能力。】
(二)课堂设计
1.知识梳理。
计算下面图形的面积,你能想出几种方法?
学生独立完成,全班交流展示不同方法。
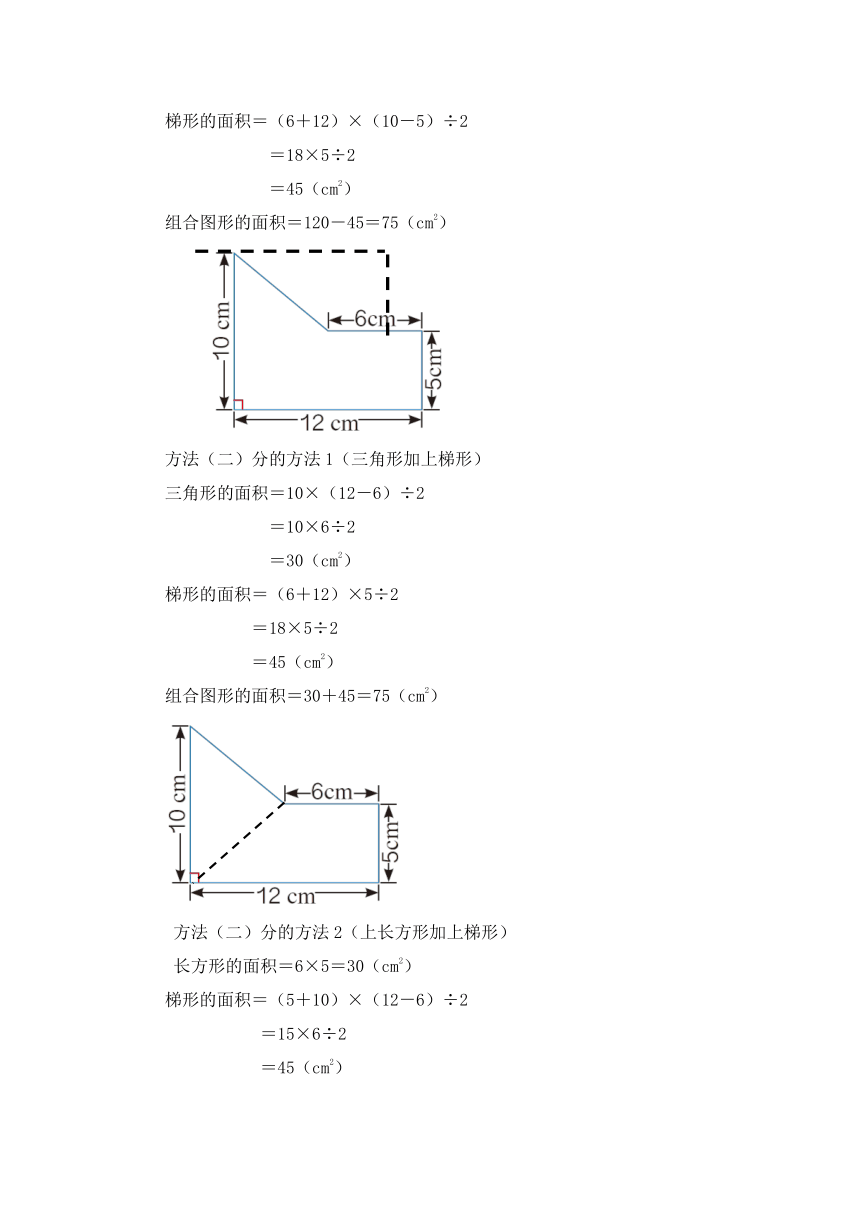
方法(一)挖的方法(长方形减去梯形)
长方形面积=12×10=120(cm2)
梯形的面积=(6+12)×(10-5)÷2
=18×5÷2
=45(cm2)
组合图形的面积=120-45=75(cm2)
方法(二)分的方法1(三角形加上梯形)
三角形的面积=10×(12-6)÷2
=10×6÷2
=30(cm2)
梯形的面积=(6+12)×5÷2
=18×5÷2
=45(cm2)
组合图形的面积=30+45=75(cm2)
方法(二)分的方法2(上长方形加上梯形)
长方形的面积=6×5=30(cm2)
梯形的面积=(5+10)×(12-6)÷2
=15×6÷2
=45(cm2)
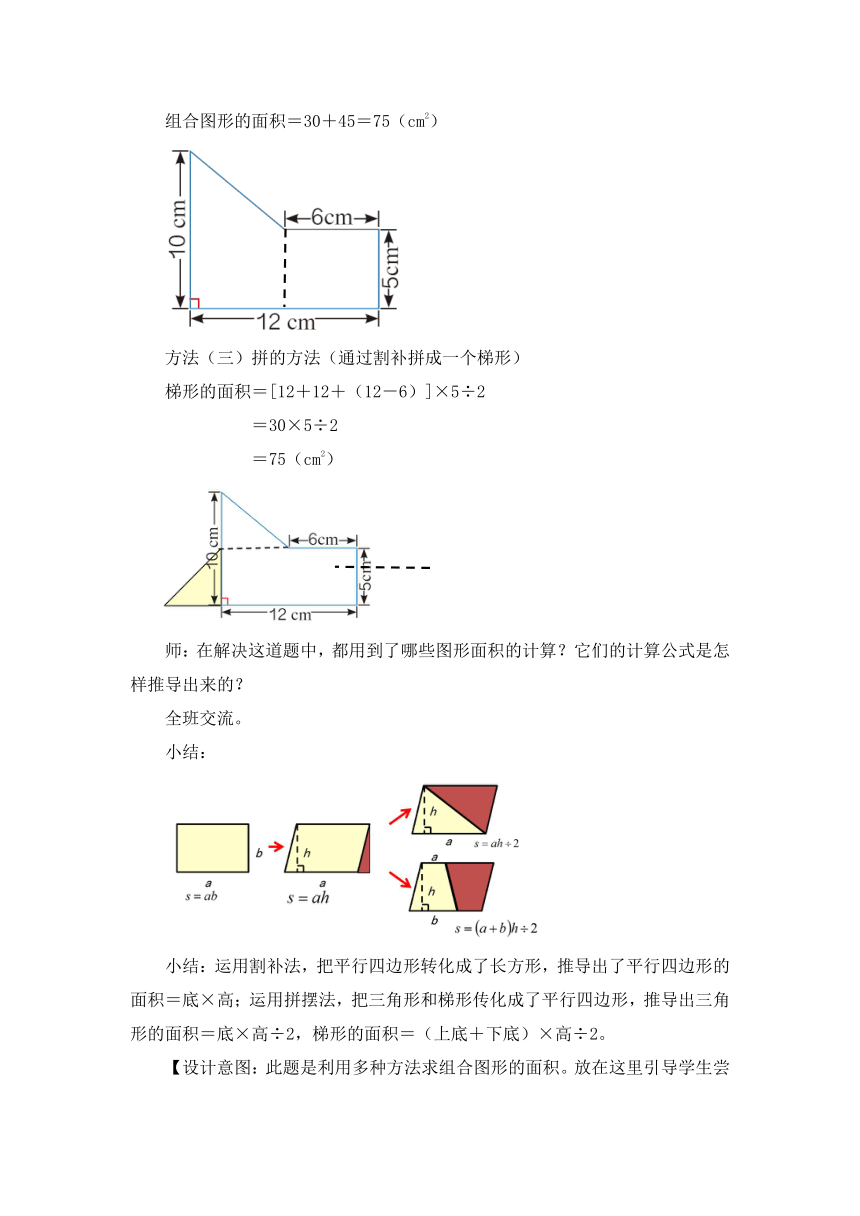
组合图形的面积=30+45=75(cm2)
方法(三)拼的方法(通过割补拼成一个梯形)
梯形的面积=[12+12+(12-6)]×5÷2
=30×5÷2
=75(cm2)
师:在解决这道题中,都用到了哪些图形面积的计算?它们的计算公式是怎样推导出来的?
全班交流。
小结:
小结:运用割补法,把平行四边形转化成了长方形,推导出了平行四边形的面积=底×高;运用拼摆法,把三角形和梯形传化成了平行四边形,推导出三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2。
【设计意图:此题是利用多种方法求组合图形的面积。放在这里引导学生尝试用多种方法求组合图形的面积,既巩固了求组合图形面积的方法,同时也复习了几种基本图形的面积公式,在解决这一问题的过程中也运用了转化的思想,有助于加强学生记忆几种基本图形面积公式的推导过程。】
2.沟通知识的联系
组内交流课前作业,在交流的过程中选出本组同学中做的最好的一份思维导图小组讨论并完善,准备展示分享。
【设计意图:引导学生在小组的交流展示、教师的补充完善的过程中梳理完善本单元知识,培养学生自主学习的意识,提高数学的自学能力。】
3.典题演练。
(1)求面积
【知识点】平行四边形、三角形、梯形面积公式。
【答案】23.4,25.8,29.58,150,21.8,150。
【解析】代入相应的面积公式,求出相应的面积。
(2)下图是教室的一面墙,如果砌这面墙平均每平方米用转185块,一共
需要多少块砖?
【知识点】求组合图形的方法,长方形的面积,三角形的面积,梯形的面积。
【答案】方法有多种,方法之一:
分割成三角形和长方形。
三角形的面积=5×1.2÷2=3(m2)
长方形的面积=5×4=20(m2)
组合图形的面积=3+20=23(m2)
23×185=4255(块)
答:一共需要4255块砖。
【解析】利用分、拼、挖的方法把组合图形转化为基本图形,进而求出组合图形的面积。
(3)求出下面每个图形的面积,再比较它们的面积,你发现了什么?(每两个点间的距离是1厘米)
【知识点】长方形的面积、平行四边形的面积、三角形的面积、梯形的面积与底和高的关系。
【答案】长方形的面积=3×4=12(cm2)
平行四边形的面积=3×4=12(cm2)
梯形的面积=(2+4)×4÷2=12(cm2)
三角形的面积=6×4÷2=12(cm2)
发现如:平行四边形和三角形面积相等时,若高相等,则三角形的底是平行四边形底的2倍。
【解析】利用每种基本图形的面积公式,代入求出面积。部分同学可以提升到把平行四边形和三角形都可以看做特殊的梯形,进一步体会转化思想在学习中的应用。
一、复习内容
《义务教育教科书数学》(人教2014版)五年级上册第86~105页。
二、复习目标
1.通过小组合作,回顾梳理本单元知识,能用思维导图清晰的整理单元知识网络,并熟练运用本单元知识解决实际问题。
2.经历单元复习过程,熟练掌握单元知识的同时,再次感受合作学习的重要性以及转化思想在数学学习中的重要性,培养良好的数学学习兴趣。
三、复习重、难点
平行四边形、三角形、梯形面积公式的推导过程;灵活运用平行四边形、三角形、梯形的面积公式解决问题。
四、配套资源
《多边形的面积复习课》教学课件
五、复习设计
(一)课前作业
复习课本P86——P105,思考本单元都学习了哪些内容?你认为学习本单元的关键在哪里?对本单元知识进行知识梳理,形成知识导图。
【设计意图:学生课前自主复习,培养自主复习的意识,提高自主复习并绘制思维导图的能力。】
(二)课堂设计
1.知识梳理。
计算下面图形的面积,你能想出几种方法?
学生独立完成,全班交流展示不同方法。
方法(一)挖的方法(长方形减去梯形)
长方形面积=12×10=120(cm2)
梯形的面积=(6+12)×(10-5)÷2
=18×5÷2
=45(cm2)
组合图形的面积=120-45=75(cm2)
方法(二)分的方法1(三角形加上梯形)
三角形的面积=10×(12-6)÷2
=10×6÷2
=30(cm2)
梯形的面积=(6+12)×5÷2
=18×5÷2
=45(cm2)
组合图形的面积=30+45=75(cm2)
方法(二)分的方法2(上长方形加上梯形)
长方形的面积=6×5=30(cm2)
梯形的面积=(5+10)×(12-6)÷2
=15×6÷2
=45(cm2)
组合图形的面积=30+45=75(cm2)
方法(三)拼的方法(通过割补拼成一个梯形)
梯形的面积=[12+12+(12-6)]×5÷2
=30×5÷2
=75(cm2)
师:在解决这道题中,都用到了哪些图形面积的计算?它们的计算公式是怎样推导出来的?
全班交流。
小结:
小结:运用割补法,把平行四边形转化成了长方形,推导出了平行四边形的面积=底×高;运用拼摆法,把三角形和梯形传化成了平行四边形,推导出三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2。
【设计意图:此题是利用多种方法求组合图形的面积。放在这里引导学生尝试用多种方法求组合图形的面积,既巩固了求组合图形面积的方法,同时也复习了几种基本图形的面积公式,在解决这一问题的过程中也运用了转化的思想,有助于加强学生记忆几种基本图形面积公式的推导过程。】
2.沟通知识的联系
组内交流课前作业,在交流的过程中选出本组同学中做的最好的一份思维导图小组讨论并完善,准备展示分享。
【设计意图:引导学生在小组的交流展示、教师的补充完善的过程中梳理完善本单元知识,培养学生自主学习的意识,提高数学的自学能力。】
3.典题演练。
(1)求面积
【知识点】平行四边形、三角形、梯形面积公式。
【答案】23.4,25.8,29.58,150,21.8,150。
【解析】代入相应的面积公式,求出相应的面积。
(2)下图是教室的一面墙,如果砌这面墙平均每平方米用转185块,一共
需要多少块砖?
【知识点】求组合图形的方法,长方形的面积,三角形的面积,梯形的面积。
【答案】方法有多种,方法之一:
分割成三角形和长方形。
三角形的面积=5×1.2÷2=3(m2)
长方形的面积=5×4=20(m2)
组合图形的面积=3+20=23(m2)
23×185=4255(块)
答:一共需要4255块砖。
【解析】利用分、拼、挖的方法把组合图形转化为基本图形,进而求出组合图形的面积。
(3)求出下面每个图形的面积,再比较它们的面积,你发现了什么?(每两个点间的距离是1厘米)
【知识点】长方形的面积、平行四边形的面积、三角形的面积、梯形的面积与底和高的关系。
【答案】长方形的面积=3×4=12(cm2)
平行四边形的面积=3×4=12(cm2)
梯形的面积=(2+4)×4÷2=12(cm2)
三角形的面积=6×4÷2=12(cm2)
发现如:平行四边形和三角形面积相等时,若高相等,则三角形的底是平行四边形底的2倍。
【解析】利用每种基本图形的面积公式,代入求出面积。部分同学可以提升到把平行四边形和三角形都可以看做特殊的梯形,进一步体会转化思想在学习中的应用。
