1.1 探索勾股定理课件

课件38张PPT。
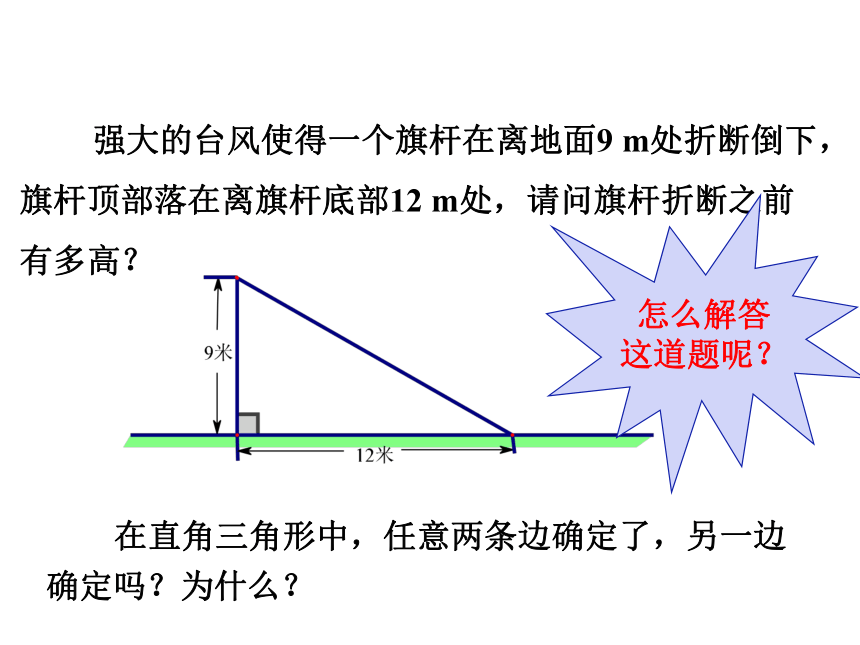
1.1 探索勾股定理 强大的台风使得一个旗杆在离地面9 m处折断倒下，
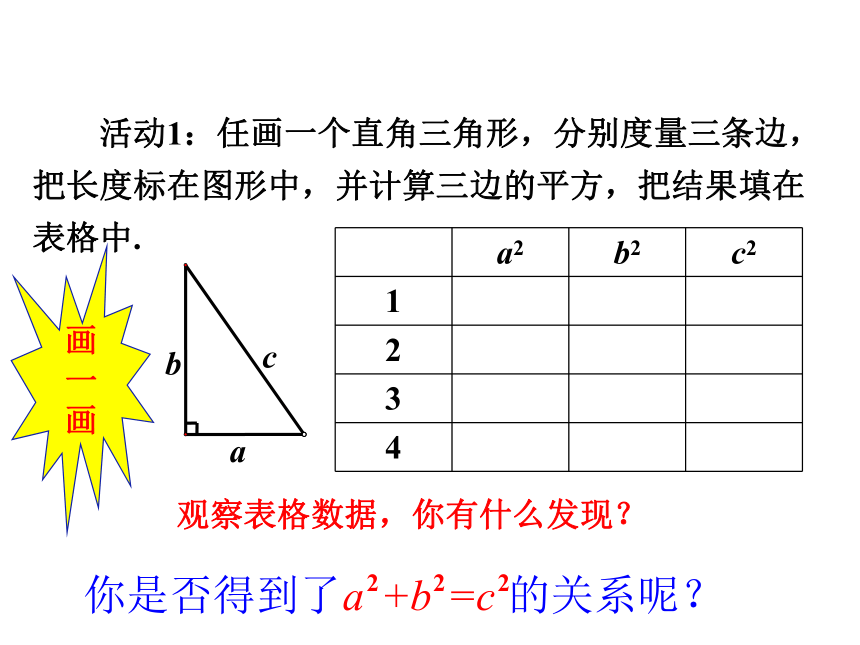
旗杆顶部落在离旗杆底部12 m处，请问旗杆折断之前有多高？ 在直角三角形中，任意两条边确定了，另一边确定吗？为什么？怎么解答这道题呢？情境导入 活动1：任画一个直角三角形，分别度量三条边，把长度标在图形中，并计算三边的平方，把结果填在表格中.观察表格数据，你有什么发现？探究新知画
一
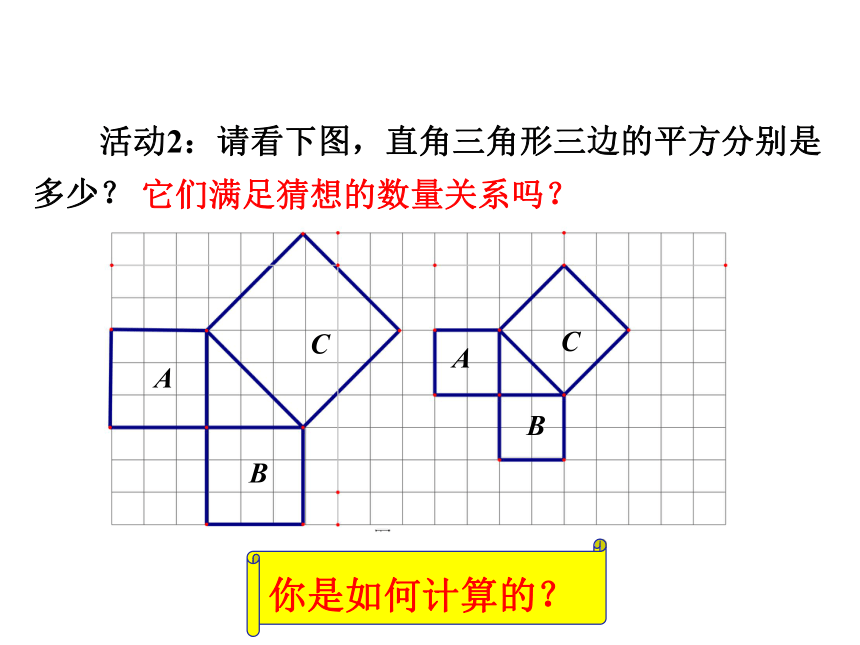
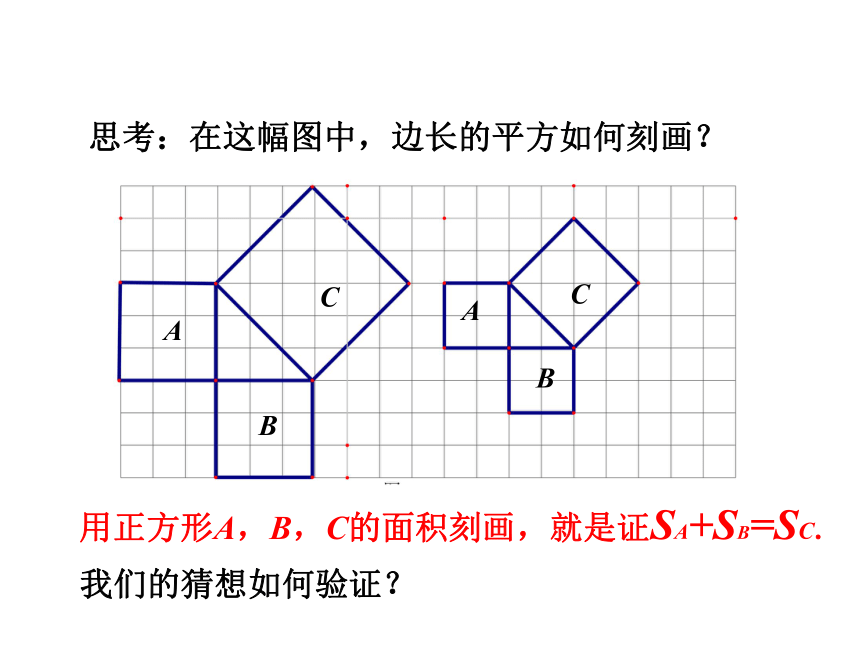
画 活动2：请看下图，直角三角形三边的平方分别是多少？ 它们满足猜想的数量关系吗？你是如何计算的？探究新知思考：在这幅图中，边长的平方如何刻画？
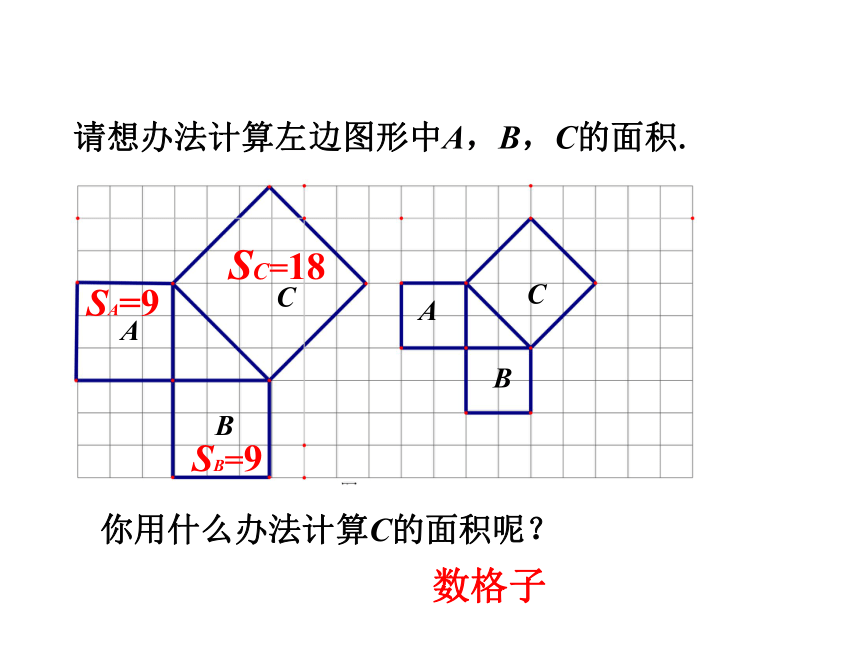
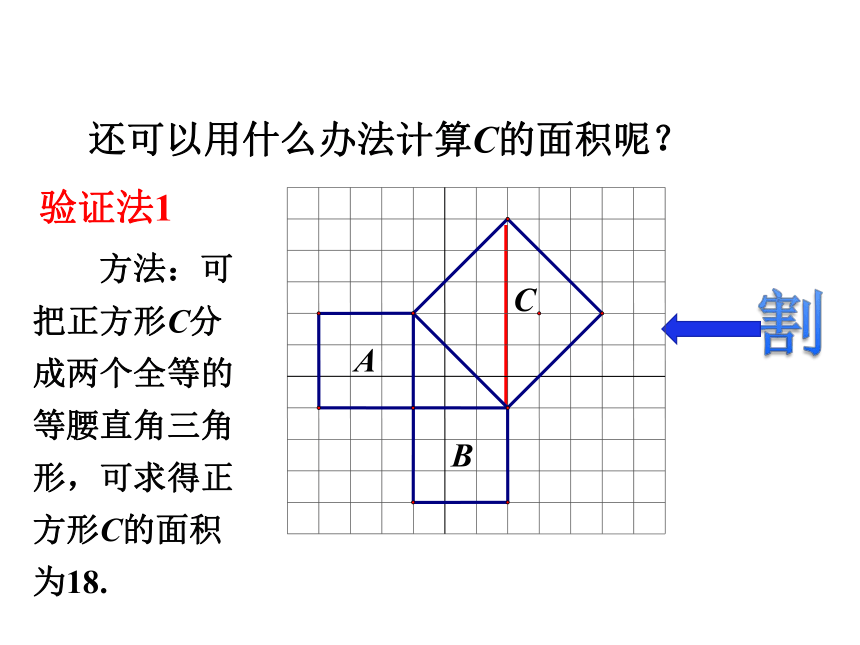
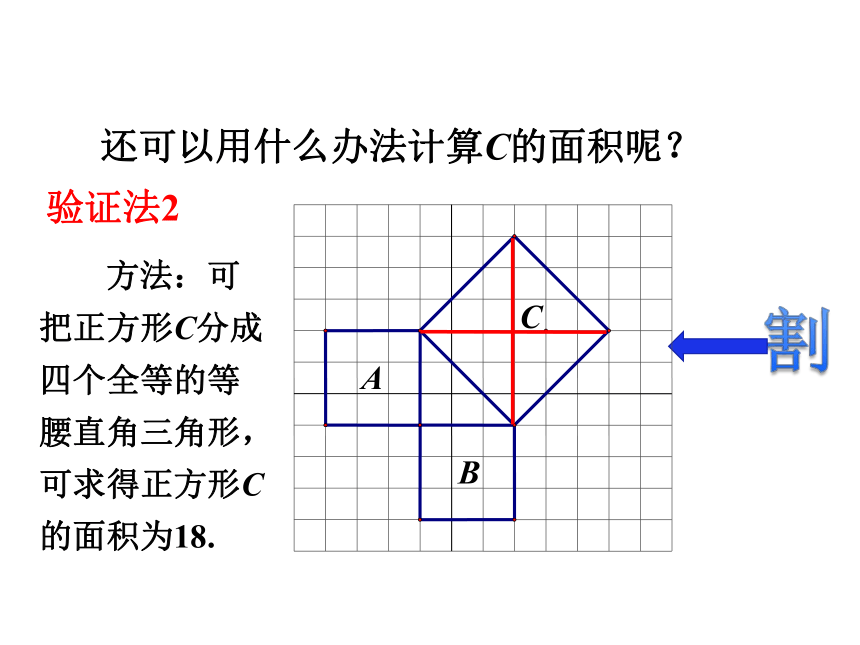
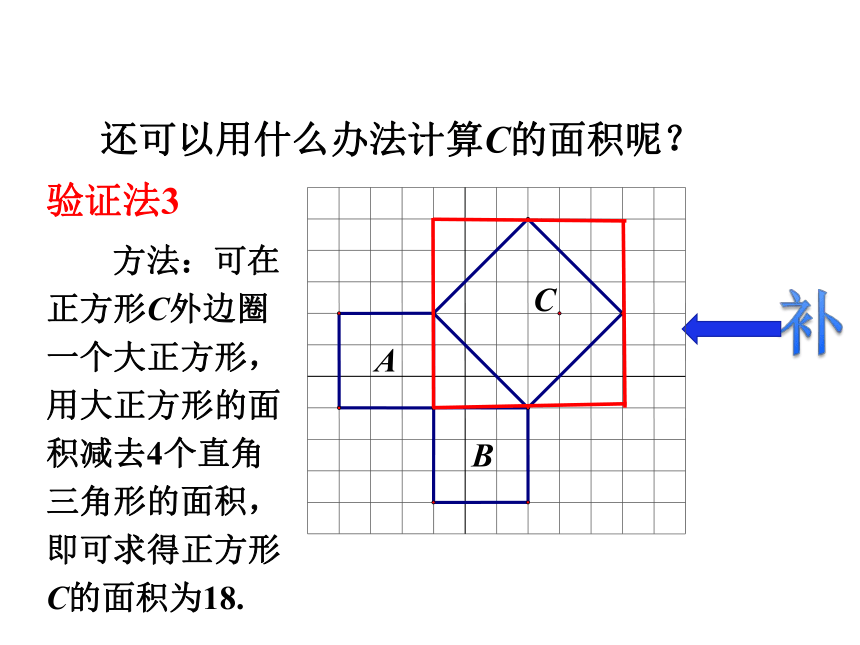
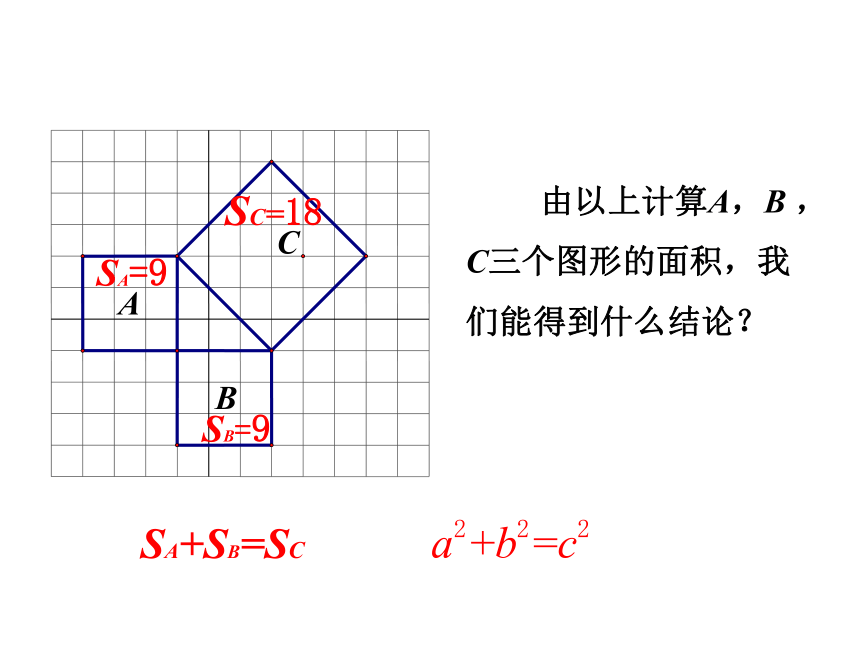
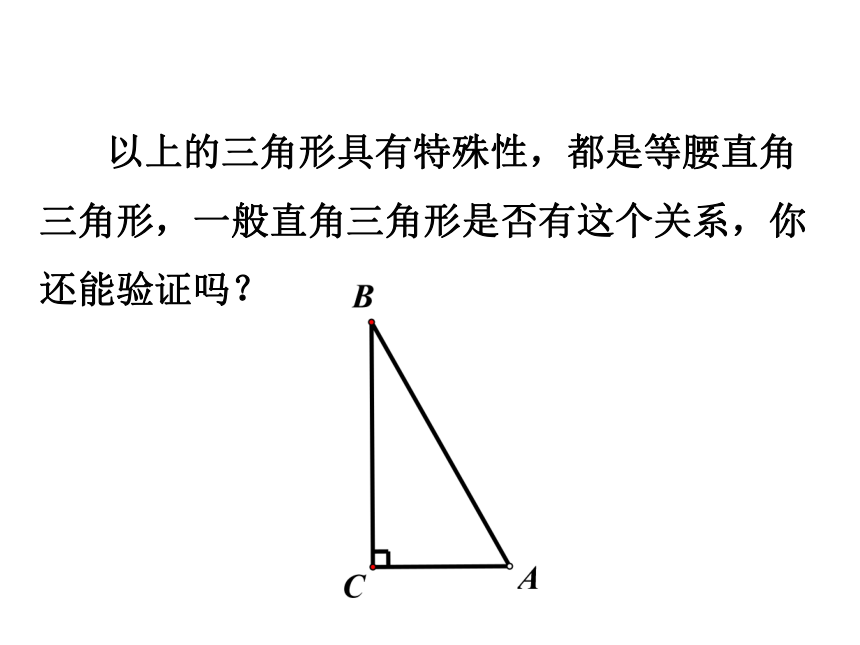
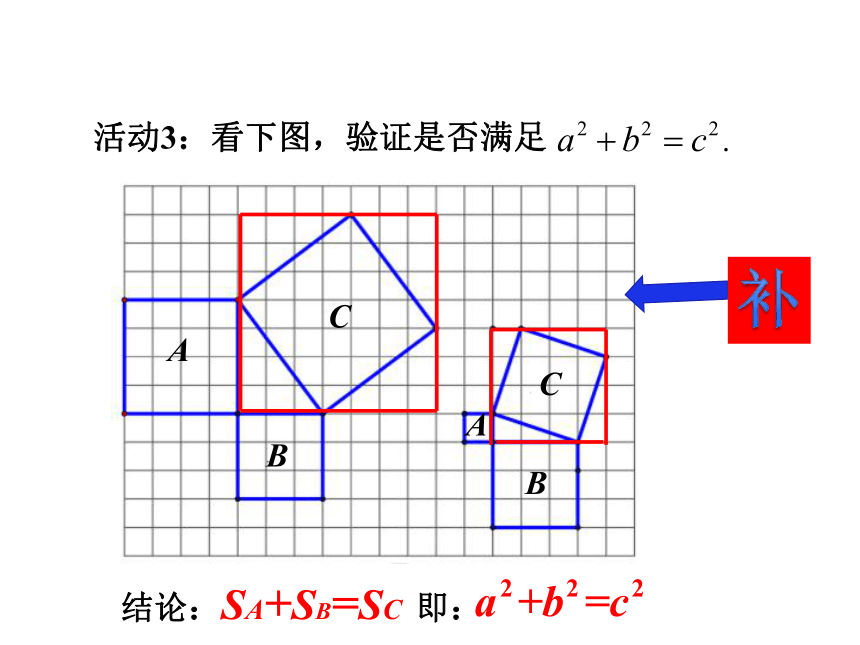
用正方形A，B，C的面积刻画，就是证SA+SB=SC.我们的猜想如何验证？探究新知请想办法计算左边图形中A，B，C的面积.你用什么办法计算C的面积呢？SA=9 SB=9SC=18探究新知数格子 方法：可把正方形C分成两个全等的等腰直角三角形，可求得正方形C的面积为18.割验证法1探究新知还可以用什么办法计算C的面积呢？ 方法：可把正方形C分成四个全等的等腰直角三角形，可求得正方形C的面积为18.割验证法2探究新知还可以用什么办法计算C的面积呢？ 方法：可在正方形C外边圈一个大正方形，用大正方形的面积减去4个直角三角形的面积，即可求得正方形C的面积为18.补验证法3探究新知还可以用什么办法计算C的面积呢？探究新知SA=9 SB=9SC=18 由以上计算A，B ， C三个图形的面积，我们能得到什么结论？SA+SB=SC 以上的三角形具有特殊性，都是等腰直角三角形，一般直角三角形是否有这个关系，你还能验证吗？ 探究新知活动3：看下图，验证是否满足补结论：SA+SB=SC 即：探究新知CBACBA为什么不用数格子的方法？结论：SA+SB=SC 即：探究新知活动3：看下图，验证是否满足 勾股定理刻画了直角三角形三边的平方关系，你能用语言描述吗？ 我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.通过以上探索可以发现：即探究新知直角三角形两直角边的平方和等于斜边的平方. 在直角三角形中，两条直角边的平方和等于斜边的平方. 在Rt△ABC中，直角边分别是a，b，斜边是c，则： 说明：勾股定理的应用条件是在直角三角形中；勾股定理是刻画直角三角形三边平方的关系.勾股定理：探究新知 勾股定理刻画了直角三角形三边的数量关系，由“形”定“数”，有“数与形的第一定理”的美称，体现了“数”与“形”的完美结合，它能解决哪些问题呢？探究新知求出下列三角形中未知边的长度.
（1） （2）解：（1）由勾股定理得：
x2=62+82=100.探究新知因为x>0，所以x=10.（2）由勾股定理得：
y2=132－52=144.因为y>0，所以y=12. 强大的台风使得一个旗杆在离地面9 m处折断倒下，旗杆顶部落在离旗杆底部12 m处，请问旗杆折断前有多高？探究新知解：设旗杆折断前有x m，由勾股定理得：（x－9）2=122+92=225.因为x－9>0，所以x－9=15，所以x=24.求出下列字母所代表的正方形的面积.正方形A面积为625正方形B面积为144探究新知BA 台风使得一个旗杆折断倒下，倒下部分长比未倒下部分长4 m，如图，旗杆顶部落在离旗杆底部12 m处，旗杆折断之前有多高？探究新知解：设未折断部分为x m，则折断部分为（x+4）m.根据题意得 即：8x=128.解得x=16.
∴x+4=20（m），16+20=36（m）. 答：旗杆折断之前有36 m高. 在Rt△ABC中，若直角边长分别是a，b，斜边长是c，
则：直角三角形的三边有怎样的关系？你是通过怎样的方法验证的？测量、数格子等复习导入 如下图，分别以直角三角形的三条边为边长向外作正方形，你能利用这幅图说明勾股定理的正确性吗？探究新知割补探究新知 如下图，分别以直角三角形的三条边为边长向外作正方形，你能利用这幅图说明勾股定理的正确性吗？ 活动1：小明的证明思路如下图，想一想：小明是怎样对大正方形进行割补的？探究新知割补 你能将所有三角形和正方形的面积用a,b,c的关系式表示出来吗？a+b大正方形ABCD的面积可以表示为：
或者 可得等式 探究新知你能用右图验证勾股定理吗？探究新知验证了勾股定理小正方形ABCD的面积可以表示为：
或者 探究新知可得等式 探究新知你能用右图验证勾股定理吗？也验证了勾股定理探究新知 割补法是几何证明题中常用的方法，要注意这种方法的应用.你还能用其他方法证明勾股定理吗？ 例 我方侦察员小王在距离东西向公路400 m处侦察，发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪，测得汽车与他相距400 m，10 s后，汽车与他相距500 m ，你能帮小王计算敌方汽车的速度吗？探究新知 思考：
1.你能求出BC的长吗？你用的是什么方法？
2.你能求出汽车的速度吗？温馨提示：
勾股定理的应用前提是在直角三角形中！探究新知 例 我方侦察员小王在距离东西向公路400 m处侦察，发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪，测得汽车与他相距400 m，10 s后，汽车与他相距500 m ，你能帮小王计算敌方汽车的速度吗？ 观察下图，判断图中三角形的三边长是否满足a2+b2=c2.议一议：探究新知 你是如何求出左侧图形中每个正方形的面积的？你得到什么结论？议一议：探究新知 结论1：若钝角三角形中较长边长为c，较短边长为a、b，则a2+b2c2.S=5 S=8S=9 如图是某沿江地区交通平面图，为了加快经济发展，该地区拟修建一条连接M,O,Q三城市的沿江高速公路，已知沿江高速公路的建设成本为5 000万元/km，该沿江高速公路的造价预计是多少？探究新知探究新知该沿江高速公路的造价预计是多少？怎样求？ 1. 如图，强大的台风使得一根旗杆在离地面3 m处折断倒下，旗杆顶部落在离旗杆底部4 m处.旗杆折断前有多高？8 m强化练习 2.1876年，美国总统伽菲尔德（James Abram Garfield）利用下图证明了勾股定理，你能利用它验证勾股定理吗？说一说这个方法和本节的探索方法的联系.强化练习