第一节 静力学
图片预览








文档简介
课件26张PPT。物理解题方法与技巧 上海市行知中学 马骏第一节 静力学主要内容:平衡态问题 平衡态问题的研究方法,从研究对象的选取看,有整体法和隔离体法;从具体的求解过程看,有定量计算法(解析法)和定性分析法;从定量计算法的运用数学知识看,又分为相似三角形法和正弦、余弦定理及直角三角形的边角关系等方法。定性分析法,因不要求定量计算,一般采用图示法(力三角形法或平行四边形法)。另外还有常见的假设法、正交分解法等。第一类:三个共点力作用下物体平衡问题 解三个共点力作用下物体平衡问题的常用方法有五种 1、力的合成、分解法 1、力的合成、分解法
对于三力平衡问题,一般可根据“任意两个力的合力与第三个力等大反向”的关系,即利用平衡条件的“等值、反向”原理解答。例题 : 如图所示,一小球在纸面内来回振动,当绳OA和OB拉力相等时,摆线与竖直方向的夹角α为( )
A. 15° B. 30° C. 45° D. 60°A第一类:三个共点力作用下物体平衡问题 解三个共点力作用下物体平衡问题的常用方法有五种 1、力的合成、分解法 2、矢量三角形法 2、矢量三角形法
物体受同一平面内三个互不平行的力作用平衡时,这三个力的矢量箭头首尾相接,构成一个矢量三角形,因此可利用三角形法,求得未知力。 例题 1 : 图中重物的质量为m,轻细线AO和BO的A、B端是固定的。平衡时AO是水平的,BO与水平面夹角为θ。AO的拉力和BO的拉力的大小是( )
B.
C. D. B D2、矢量三角形法
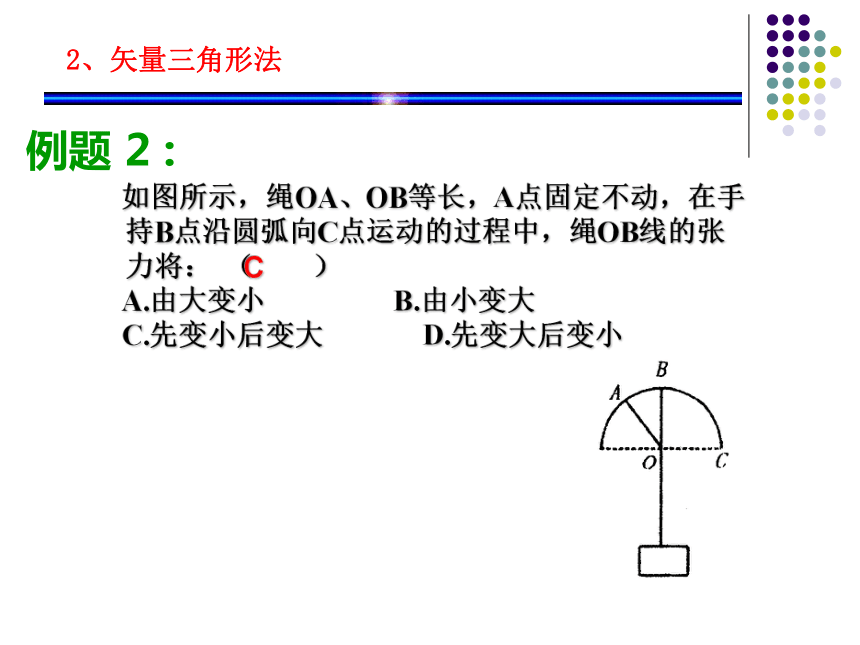
例题 2 : 如图所示,绳OA、OB等长,A点固定不动,在手持B点沿圆弧向C点运动的过程中,绳OB线的张力将: ( )
A.由大变小 B.由小变大
C.先变小后变大 D.先变大后变小C第一类:三个共点力作用下物体平衡问题 解三个共点力作用下物体平衡问题的常用方法有五种 1、力的合成、分解法 3、三力汇交原理 2、矢量三角形法 3、三力汇交原理
如果一个物体受到三个不平行外力的作用而平衡,这三个力的作用线必在同一平面上,而且必为共点力。例题 : 如图所示,两光滑板AO、BO与水平面夹角都是60o,一轻质细杆水平放在其间,用竖直向下的力F作用在轻杆中间,杆对两板的压力大小为_______。第一类:三个共点力作用下物体平衡问题 解三个共点力作用下物体平衡问题的常用方法有五种 1、力的合成、分解法 3、三力汇交原理 2、矢量三角形法 4、相似三角形法 4、相似三角形法
利用力三角形与几何三角形相似,两个三角形的对应边成比例,从而求未知力 例题 : 固定在水平面上光滑半球,球心O的正上方固定一个小定滑轮,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮,如图所示.今缓慢拉绳使小球从A点滑到半球顶点,则此过程中,小球对半球的压力大小N及细绳的拉力大小T的变化情况是:( )
A.N变大,T变大; B.N变小,T变大;
C.N不变,T变小; D.N变大,T变小.图10C第一类:三个共点力作用下物体平衡问题 解三个共点力作用下物体平衡问题的常用方法有五种 1、力的合成、分解法 3、三力汇交原理 2、矢量三角形法 4、相似三角形法 5、拉密定理(正弦定理)法 5、拉密定理(正弦定理)法
三个共点力平衡时,每个力与另外两个力夹角的正弦之比均相等,这个结论叫拉密定理。表达式为:F1 /sinα= F2/sinβ=F3 /sinγ例题 : 如图甲表示一种简易起重机,OA是钢绳,跟水平方向成30°角;OB是撑杆,跟水平方向成60°角。提起的货物重5×103N,求钢绳的拉力和撑杆的支持力各多大?(撑杆自重不计) 根据拉密定理有:
F2/sin60°=F1/sin150°=F/sin150°
则求得:F1 =F2≈8.7×103N。 第二类:多个共点力作用下物体平衡问题 解多个共点力作用下物体平衡问题的常方法 正交分解法。
可将各力分别分解到轴上和轴上,运用两坐标轴上的合力等于零的条件,即 、 求解,值得注意的是,对x、y方向选择时,要尽可能使落在x、y轴上的力多,且被分解的力尽可能是已知力,不宜分解待求力。 如图所示,只要使连杆AB与滑块m所在平面间的夹角θ大于某个值,那么,无论连杆AB对滑块施加多大的作用力,都不可能使之滑动,且连杆AB对滑块施加的作用力越大,滑块就越稳定,工程力学上称之为“自锁”现象。为使滑块能“自锁”, θ应满足什么条件?(设滑块与所在平面间的动摩擦因数为μ)例题 : 第三类:整体法与隔离法整体法
整体法是以物体系统为研究对象,从整体或全过程去把握物理现象的本质和规律,是一种把具有相互联系、相互依赖、相互制约、相互作用的多个物体,多个状态,或者多个物理变化过程组合作为一个融洽加以研究的思维形式。 隔离法
隔离法就是从整个系统中将某一部分物体隔离出来,然后单独分析被隔离部分的受力情况和运动情况,从而把复杂的问题转化为简单的一个个小问题求解。 例题 1:如图所示,三个相同的物体叠放在一起,当作用在B物体上的水平力F为2牛顿时,三个物体都静止,则物体A与B之间、B与C之间,C与桌面之间的摩擦力大小分别为: ( )
A.0,0,0 B.0,1牛,1牛
C.0,2牛,2牛 D.2牛,2牛,2牛C例题 2:如图12所示,两块相同的竖直木板之间有质量均为的四块相同的砖,用两个大小为F的水平压力压木板,使砖块静止不动。设所有接触面均粗糙,则第3块砖对第2块砖的摩擦力为( )
A. 0 B. 0.5mg C. mg D. 2mgA例题 3:用轻质细线把两个质量未知的小球悬挂起来,如图1—2所示,今对小球a持续施加一个向左偏下30°的恒力,并对小球b持续施加一个向右偏上30°的同样大小的恒力,最后达到平衡,表示平衡状态的图可能是 ( )解析:先以小球a、b及连线组成的系统为研究对象,因为系统处于平衡状态,所受合力必为零,由于Fa、Fb大小相等,方向相反,可以抵消,而(ma+mb)g的方向竖直向下,所以悬线对系统的拉力T1的方向必然竖直向上.再以b球为研究对象,故应选A.例题 4:有一个直角架AOB,OA水平放置,表面粗糙,OB竖直向下,表面光滑,OA上套有小环P,OB上套有小环Q,两个环的质量均为m,两环间由一根质量可忽略、不何伸长的细绳相连,并在某一位置平衡,如图1—4所示.现将P环向左移动一段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态相比,OA杆对P环的支持力N和细绳上的拉力T的变化情况是 ( )
A.N不变,T变大 B.N不变,T变小
C.N变大,T变小 D.N变大,T变大解析:先把P、Q看成一个整体,竖直方向上只受重力和OA杆 对它的支持力,所以N不变,始终等于P、Q的重力之和。再以Q为研究对象,拉力T应变小.由以上分析可知应选B.第四类:共点力作用下物体平衡的极值问题 共点力作用下物体平衡的极值问题
指研究平衡问题中某个力变化时出现的最大值或最小值,处理这类问题常用解析法和图解法。 例题 : 有一重量为G的木块与水平地面间的动摩擦因数为μ,一人欲用最小的作用力F使木块做匀速运动,则此最小作用力的大小和方向应如何?第五类:轻杆受力问题1. 杆受力处于平衡状态,一端可以自由转动,则另一端 所受合力必沿杆方向。 2. 轻杆受力处于平衡状态,一端固定时,杆可以承受来自各个方向的力,从而杆的受力不一定沿杆方向,应具体问题具体分析。例题 : 如图所示,AB为水平轻杆,A端用绞链与墙壁相连,B端用轻绳CB拉着,且与AB成角,下端挂一重为10N的物体,求AB杆受到的作用力?例题 : 水平横梁的一端A插在墙壁内,另一端装有一小滑轮B,一轻绳的一端固定在墙上,另一端跨过滑轮后挂着一质量为m的物体,并与横梁夹角为30o,如图22所示,求横梁B端受到的作用力? F=100N
对于三力平衡问题,一般可根据“任意两个力的合力与第三个力等大反向”的关系,即利用平衡条件的“等值、反向”原理解答。例题 : 如图所示,一小球在纸面内来回振动,当绳OA和OB拉力相等时,摆线与竖直方向的夹角α为( )
A. 15° B. 30° C. 45° D. 60°A第一类:三个共点力作用下物体平衡问题 解三个共点力作用下物体平衡问题的常用方法有五种 1、力的合成、分解法 2、矢量三角形法 2、矢量三角形法
物体受同一平面内三个互不平行的力作用平衡时,这三个力的矢量箭头首尾相接,构成一个矢量三角形,因此可利用三角形法,求得未知力。 例题 1 : 图中重物的质量为m,轻细线AO和BO的A、B端是固定的。平衡时AO是水平的,BO与水平面夹角为θ。AO的拉力和BO的拉力的大小是( )
B.
C. D. B D2、矢量三角形法
例题 2 : 如图所示,绳OA、OB等长,A点固定不动,在手持B点沿圆弧向C点运动的过程中,绳OB线的张力将: ( )
A.由大变小 B.由小变大
C.先变小后变大 D.先变大后变小C第一类:三个共点力作用下物体平衡问题 解三个共点力作用下物体平衡问题的常用方法有五种 1、力的合成、分解法 3、三力汇交原理 2、矢量三角形法 3、三力汇交原理
如果一个物体受到三个不平行外力的作用而平衡,这三个力的作用线必在同一平面上,而且必为共点力。例题 : 如图所示,两光滑板AO、BO与水平面夹角都是60o,一轻质细杆水平放在其间,用竖直向下的力F作用在轻杆中间,杆对两板的压力大小为_______。第一类:三个共点力作用下物体平衡问题 解三个共点力作用下物体平衡问题的常用方法有五种 1、力的合成、分解法 3、三力汇交原理 2、矢量三角形法 4、相似三角形法 4、相似三角形法
利用力三角形与几何三角形相似,两个三角形的对应边成比例,从而求未知力 例题 : 固定在水平面上光滑半球,球心O的正上方固定一个小定滑轮,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮,如图所示.今缓慢拉绳使小球从A点滑到半球顶点,则此过程中,小球对半球的压力大小N及细绳的拉力大小T的变化情况是:( )
A.N变大,T变大; B.N变小,T变大;
C.N不变,T变小; D.N变大,T变小.图10C第一类:三个共点力作用下物体平衡问题 解三个共点力作用下物体平衡问题的常用方法有五种 1、力的合成、分解法 3、三力汇交原理 2、矢量三角形法 4、相似三角形法 5、拉密定理(正弦定理)法 5、拉密定理(正弦定理)法
三个共点力平衡时,每个力与另外两个力夹角的正弦之比均相等,这个结论叫拉密定理。表达式为:F1 /sinα= F2/sinβ=F3 /sinγ例题 : 如图甲表示一种简易起重机,OA是钢绳,跟水平方向成30°角;OB是撑杆,跟水平方向成60°角。提起的货物重5×103N,求钢绳的拉力和撑杆的支持力各多大?(撑杆自重不计) 根据拉密定理有:
F2/sin60°=F1/sin150°=F/sin150°
则求得:F1 =F2≈8.7×103N。 第二类:多个共点力作用下物体平衡问题 解多个共点力作用下物体平衡问题的常方法 正交分解法。
可将各力分别分解到轴上和轴上,运用两坐标轴上的合力等于零的条件,即 、 求解,值得注意的是,对x、y方向选择时,要尽可能使落在x、y轴上的力多,且被分解的力尽可能是已知力,不宜分解待求力。 如图所示,只要使连杆AB与滑块m所在平面间的夹角θ大于某个值,那么,无论连杆AB对滑块施加多大的作用力,都不可能使之滑动,且连杆AB对滑块施加的作用力越大,滑块就越稳定,工程力学上称之为“自锁”现象。为使滑块能“自锁”, θ应满足什么条件?(设滑块与所在平面间的动摩擦因数为μ)例题 : 第三类:整体法与隔离法整体法
整体法是以物体系统为研究对象,从整体或全过程去把握物理现象的本质和规律,是一种把具有相互联系、相互依赖、相互制约、相互作用的多个物体,多个状态,或者多个物理变化过程组合作为一个融洽加以研究的思维形式。 隔离法
隔离法就是从整个系统中将某一部分物体隔离出来,然后单独分析被隔离部分的受力情况和运动情况,从而把复杂的问题转化为简单的一个个小问题求解。 例题 1:如图所示,三个相同的物体叠放在一起,当作用在B物体上的水平力F为2牛顿时,三个物体都静止,则物体A与B之间、B与C之间,C与桌面之间的摩擦力大小分别为: ( )
A.0,0,0 B.0,1牛,1牛
C.0,2牛,2牛 D.2牛,2牛,2牛C例题 2:如图12所示,两块相同的竖直木板之间有质量均为的四块相同的砖,用两个大小为F的水平压力压木板,使砖块静止不动。设所有接触面均粗糙,则第3块砖对第2块砖的摩擦力为( )
A. 0 B. 0.5mg C. mg D. 2mgA例题 3:用轻质细线把两个质量未知的小球悬挂起来,如图1—2所示,今对小球a持续施加一个向左偏下30°的恒力,并对小球b持续施加一个向右偏上30°的同样大小的恒力,最后达到平衡,表示平衡状态的图可能是 ( )解析:先以小球a、b及连线组成的系统为研究对象,因为系统处于平衡状态,所受合力必为零,由于Fa、Fb大小相等,方向相反,可以抵消,而(ma+mb)g的方向竖直向下,所以悬线对系统的拉力T1的方向必然竖直向上.再以b球为研究对象,故应选A.例题 4:有一个直角架AOB,OA水平放置,表面粗糙,OB竖直向下,表面光滑,OA上套有小环P,OB上套有小环Q,两个环的质量均为m,两环间由一根质量可忽略、不何伸长的细绳相连,并在某一位置平衡,如图1—4所示.现将P环向左移动一段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态相比,OA杆对P环的支持力N和细绳上的拉力T的变化情况是 ( )
A.N不变,T变大 B.N不变,T变小
C.N变大,T变小 D.N变大,T变大解析:先把P、Q看成一个整体,竖直方向上只受重力和OA杆 对它的支持力,所以N不变,始终等于P、Q的重力之和。再以Q为研究对象,拉力T应变小.由以上分析可知应选B.第四类:共点力作用下物体平衡的极值问题 共点力作用下物体平衡的极值问题
指研究平衡问题中某个力变化时出现的最大值或最小值,处理这类问题常用解析法和图解法。 例题 : 有一重量为G的木块与水平地面间的动摩擦因数为μ,一人欲用最小的作用力F使木块做匀速运动,则此最小作用力的大小和方向应如何?第五类:轻杆受力问题1. 杆受力处于平衡状态,一端可以自由转动,则另一端 所受合力必沿杆方向。 2. 轻杆受力处于平衡状态,一端固定时,杆可以承受来自各个方向的力,从而杆的受力不一定沿杆方向,应具体问题具体分析。例题 : 如图所示,AB为水平轻杆,A端用绞链与墙壁相连,B端用轻绳CB拉着,且与AB成角,下端挂一重为10N的物体,求AB杆受到的作用力?例题 : 水平横梁的一端A插在墙壁内,另一端装有一小滑轮B,一轻绳的一端固定在墙上,另一端跨过滑轮后挂着一质量为m的物体,并与横梁夹角为30o,如图22所示,求横梁B端受到的作用力? F=100N
