第二节 运动学（提高篇）

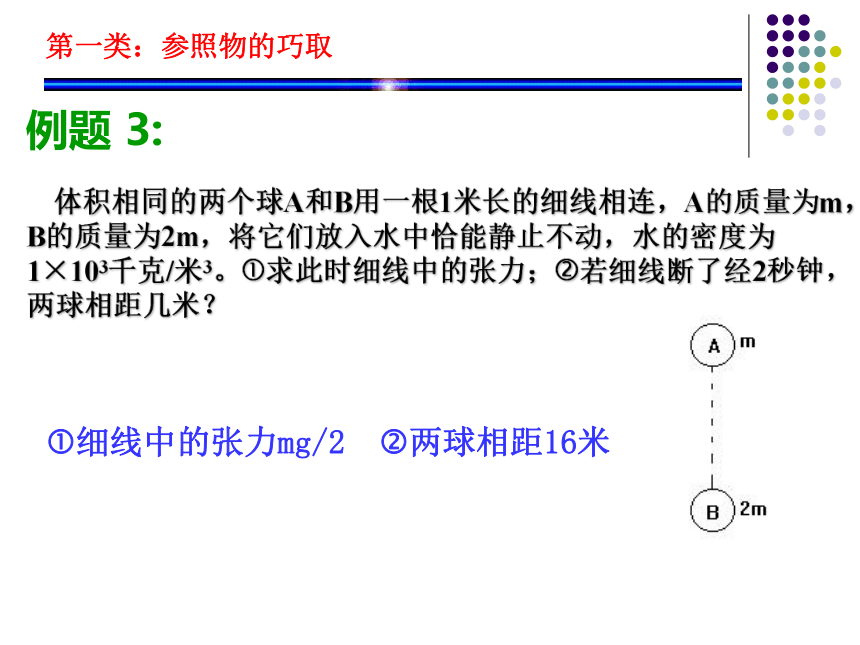
课件32张PPT。第二节 运动学主要内容： 《运动学》要解决的问题是如何描述物体的运动。高中阶段以匀变速直线运动为主，其描述的方法有：解析法（公式法）和图像法。第一类：参照物的巧取 运动是绝对的，而对物体运动的描述是相对的。同样一个物体的运动，由于参照物的选取不同，其描述的结果是不同的。正因如此，若在不涉及运动原因的前提下，可以通过参照物的选取简化运动的数学描述，从而达到简化解题的目的。第一类：参照物的巧取 例题 1: 升降机高2.5米，一小球从天花板上脱落，（g=10m/s2）
若升降机静止，小球下落至底板的时间为_______秒；
若升降机以5m/s的速度匀速下降，小球下落至底板的时间为_______秒；
若升降机以5m/s2的加速度匀加速下降，小球下落至底板的时间为______秒；
若升降机以5m/s2的加速度匀加速上升，小球下落至底板的时间为______秒；0.710.7110.58第一类：参照物的巧取 例题 2: 以速度v1运行的火车A上的司机看见在A的前面距离d处有一列货车B正在与A同一轨道上以速度v2同向行驶，且v2 ⑴匀减速至静止的运动，对称于初速度为0、等加速度的 反向匀加速运动；
⑵竖直上抛运动对称于自由落体运动。第二类：运动的对称性 例题 1: 一个竖直上抛的物体，到达最高点的最后1秒内上升的高度是它上升的最大高度的四分之一，则此物体能够上升的最大高度为多少？H=20m第二类：运动的对称性 例题 2: 一木块沿光滑斜面从底部开始匀减速向上滑行，它上滑到最高点的最后1秒内滑行的长度是它向上滑行的最大长度的九分之一，若斜面倾角300，求它的初速度？v0=15m/s 第三类：运动的比例关系 对初速度为零的匀变速直线运动，有许多常用的比例关系，掌握这些关系的推导与证明，并将这些比例关系灵活地在解题中加以应用，是解运动学习题的能力的体现。 初速度为零的匀变速直线运动的常用比例关系：第三类：运动的比例关系 初速度为零的匀变速直线运动的常用比例关系：1、前一个t秒内、前二个t秒内、……前N个t秒内的位移之比：
2、第一个t秒内、第二个t秒内、……第n个t秒内的位移之比：
3、t秒末、2t秒末、……nt秒末的速度之比：
4、前一个s、前二个s、……前n个s的位移所需时间之比：
5、第一个s、第二个s、……第n个s的位移所需时间之比：
6、第一个s末、第二个s末、……第n个s末的速度之比：
第三类：运动的比例关系例题 1: 物体由静止开始作匀加速直线运动，通过位移s时的速度为v，则它通过s/3的速度多大？ 第三类：运动的比例关系例题 2: 屋檐定时滴下水滴，当第5滴正欲滴下时，第1滴恰好落至地面，而第2滴与第3滴正好分别位于高1m 的窗户的上下沿，由此可知此屋檐离地面的高度为______，滴水时间间隔为_______。（g=10m/s2）第四类：运动图像法 用图象来描述物体的运动是运动描述的两大方法之一，具有形象、直观的特点，图象法解题是高中物理解题的一项基本而简便的方法。第四类：运动图像法例题 1: 一列火车进站前关闭发动机，让其匀减速滑行，当其滑行100秒后，速度减为关机时的一半，然后又继续滑行500米而停在站台内，则关机时的速度为 ___，滑行中的加速度为 ____，火车一共滑行的距离为 ___。V0=20m/sa=－0.1m/s2 s=2000m 第四类：运动图像法例题 2: 一物体从某一高度有静止开始滑下，第一次经光滑斜面滑至底面的时间为t1，第二次经光滑折面滑至底面的时间为t2，设两次通过的路程相等，试比较t1、t2的大小。第四类：运动图像法例题 3: 在地面上以初速度2V0竖直上抛一物体A后，又以初速V0同地点竖直上抛另一物体B，若要使两物体能在空中相遇，则两物体抛出的时间间隔必须满足什么条件？（不计空气阻力）第五类：平均速度法 匀变速直线运动的平均速度 ，解题中灵活加以应用，将使解题简便。第五类：平均速度法例题1 : 启动后做匀加速运动的汽车上的司机，发现尚有乘客未上车，急忙使汽车作匀减速运动直至停止，若整个过程历时t秒，行驶s米，那么，此过程中汽车的最大速度为： （ ）D第五类：平均速度法例题2 : 汽车自O点出发从静止开始在平直公路上做匀加速直线运动，途中在6s钟内分别经过P、Q两根电杆，已知P、Q电杆相距60m，车经过电杆Q时的速率是15m／s，则
A．经过P杆时的速率是5m／s
B．车的加速度是 1.5m／s2
C．P、O间距离是7.5m
D．车从出发到Q所用的时间是9s答案：A C D第六类：匀变速直线运动规律的三个推论 1、任意两个连续相等的时间（T）内的位移之差相等。
S2-S1 = S3 -S2 =……= SN-SN-1 =△S = aT2 2、在任意一段时间内，中间时刻的瞬时速度V中时等于
这段时间内的平均速度。
3、在任意一段位移内，其中点位置的瞬时速度为：
第六类：匀变速直线运动规律的三个推论例题 1: 一质点做初速度为零的匀加速直线运动，若运动后第3秒末至第5秒末的位移为40米，则质点在头4秒内的位移为多少？第3秒末的速度为多少？s=40m V3=15m/s 第六类：匀变速直线运动规律的三个推论例题 2: 质点做匀加速直线运动，第1秒内的平均速度为3米/秒，第1秒末的速度为4米/秒，则该质点运动的初速度
为_________，加速度为__________。V0=2m/s a=2m/s2 第七类：追击、相遇问题的处理 一般常用的牵连关系如下：
⑴匀减速追匀速时，恰好追上或恰好追不上的临界条件是：
——即将靠拢时速度相等；
⑵初速为零的匀加速追赶匀速时，追上前二者间具有最大
距离的条件是：
——二者的速度相等；第七类：追击、相遇问题的处理例题 1: 一辆汽车在十字路口等候绿灯，当绿灯亮时汽车以3m/s2的加速度开始行驶，恰在此时，一辆自行车以6m/s的速度匀速驶过，试求： 汽车从路口开动后，在追上自行车之前，经过多少时间两车距离最远？该最大距离为多少？什么时候汽车追上自行车？此时汽车的速度多大？t=2s s=6m V=15m/s t=4/s 第七类：追击、相遇问题的处理例题 2: 一辆汽车以初速度v0加速度a作匀减速运动，追赶在它前面s处以速度v同向匀速行驶的货车，已知v0>v，试问汽车能够追上货车的条件是什么？若汽车追不上货车，则两车间最小距离为多少？第七类：追击、相遇问题的处理例题 3: 甲、乙两车行驶在一条平直公路上，甲在后做速度为vo的匀速运动，乙在前做初速为零的匀加速运动，加速度为a，两车同向而行，开始时两车在运动方向上相距s，则vo、a、s满足关系式_________时，两车相遇两次。第八类：运动的合成与分解 描述运动的物理量许多是矢量，其运算法则为平行四边形法则，所以运动的合成与分解遵循平行四边形法则。
此类问题的重要内容是：速度的合成与分解。
其常用方法如下：
⑴根据实际效果；⑵通过位移（微元法）。
第八类：运动的合成与分解例题 1: 有一船准备渡河，已知水流速度为v=1m/s，船在静水中的航速为v ，=2m/s，则：
1、要使船能够垂直地渡过河去，那么应向何方划船？
2、要使船能在最短时间内渡河，应向何方划船？ 河宽300米，河水流速3m米/秒，船在静水中的航速为1米/秒，则该船渡河的最短时间为_________，渡河的最短位移为 _________ 。t=300s s=900m 第八类：运动的合成与分解例题 2: 如图所示，纤绳以恒定速率v沿水平方向通过定滑轮牵引小船靠岸，则船靠岸的速度是_________，若使船匀速靠岸，则纤绳的速度是________。（填：匀速、加速、减速）减速 第八类：运动的合成与分解例题 3: 如图所示，质量相等的两个小球A和B，通过轻绳绕过两个光滑的定滑轮带动C球上升，某时刻连接C球的两绳的夹角为θ ，设A、B两小球此时下落的速度为v，则C球上升的速度为（ ）
A．v/cos(θ /2) B. vcos(θ /2)
C. v/cos θ D. vcos θ
答案：A θ一人骑自行车向西行驶，当车速为4m/s时，他感觉到风从正南方向吹来，当车速增加到7m/s时，他感觉到风从东南（东偏南45°）方向吹来，则风对地的速度大小为（ ）
A、4m/s B、5m/s
C、6m/s D、7m/sB第八类：运动的合成与分解例题 4: