鲁教版(五四制)六年级上册第一章丰富的图形世界丰富的图形世界填空题练习(含答案)
文档属性
| 名称 | 鲁教版(五四制)六年级上册第一章丰富的图形世界丰富的图形世界填空题练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-07-31 22:24:28 | ||
图片预览


文档简介
丰富的图形世界填空题练习
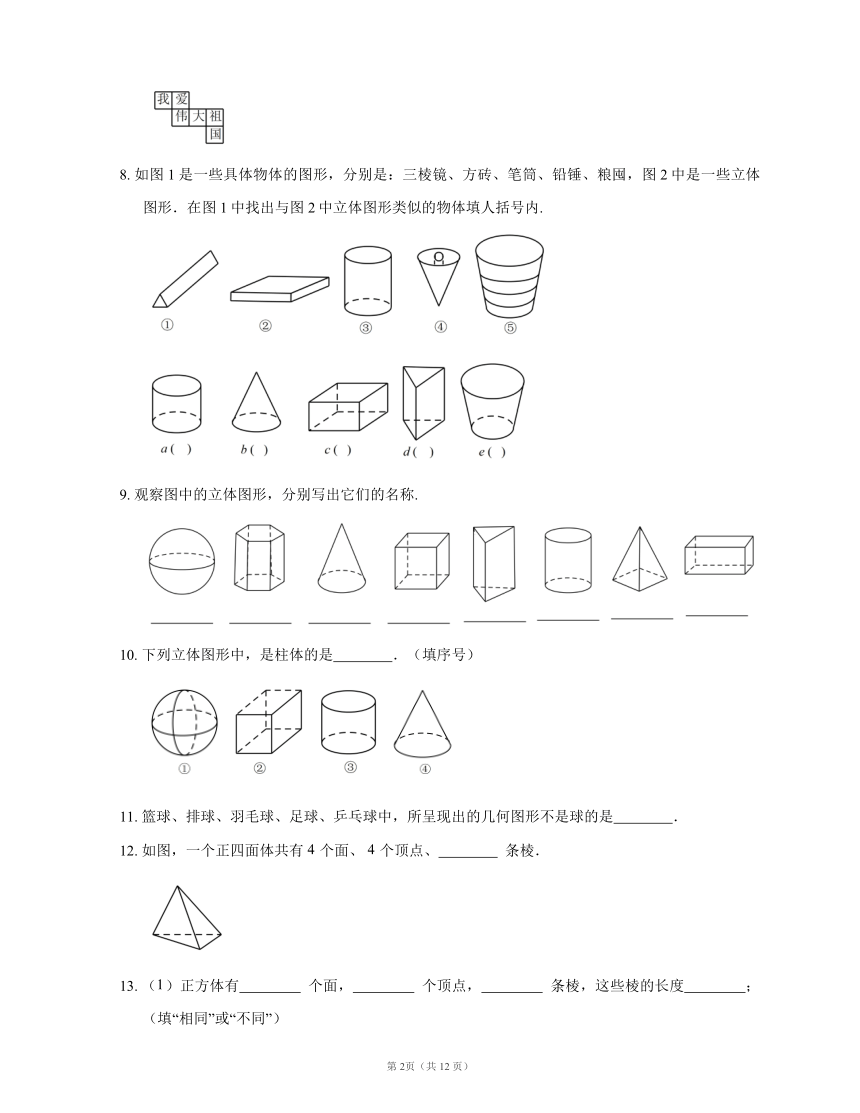
1. 如图中的截面分别是() ?() ?.
2. 正方体或长方体是一个立体图形,它是由 ? 个面, ? 条棱, ? 个顶点组成的.
3. 分别写出表面能展开成如图所示的 个平面图形的几何体的名称.
4. 用平行于圆锥的底面的平面去截圆锥,则得到的截面是 ? 形.
5. 如图是六个棱长为 的小立方块组成的一个几何体,从上面看得到的图形的面积为 ?.
6. 如图,该图形经过折叠可以围成一个正方体,折好以后与“细”字相对的字是 ?.
7. 如图,是正方体的一个平面展开图,在这个正方体中,与“爱”字所在面相对的面上的汉字是 ?.
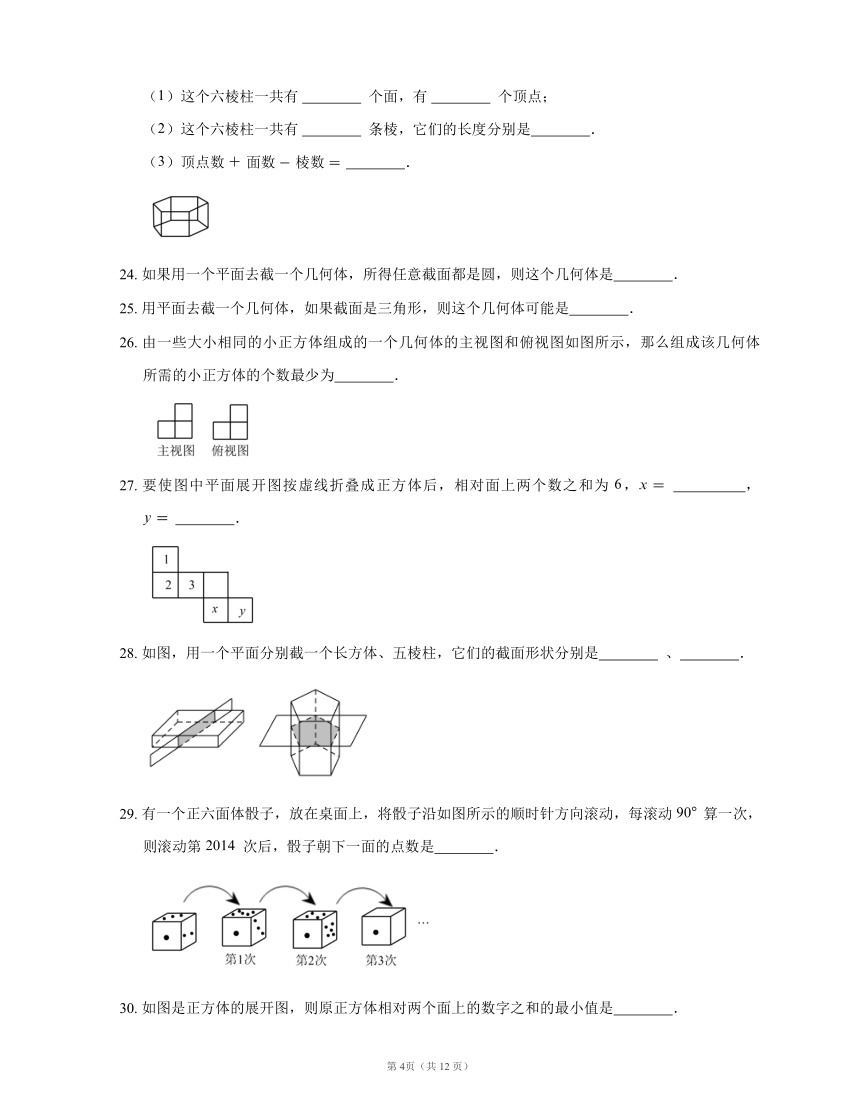
8. 如图1是一些具体物体的图形,分别是:三棱镜、方砖、笔筒、铅锤、粮囤,图2中是一些立体图形.在图1中找出与图2中立体图形类似的物体填人括号内.
9. 观察图中的立体图形,分别写出它们的名称.
10. 下列立体图形中,是柱体的是 ?.(填序号)
11. 篮球、排球、羽毛球、足球、乒乓球中,所呈现出的几何图形不是球的是 ?.
12. 如图,一个正四面体共有 个面、 个顶点、 ? 条棱.
13. ()正方体有 ? 个面, ? 个顶点, ? 条棱,这些棱的长度 ?;(填“相同”或“不同”)
()圆柱有 ? 个面,其中有 ? 个平面,还有一个面是 ? 面;
()若一个棱柱的底面是一个七边形,则它的侧面必须有 ? 个长方形,它一共有 ? 个面.
14. 下列图形中,都是柱体的一组是 ?.
15. 请在如图所示的横线上填写几何体的名称.
16. 从三个不同方向看都是同一平面图形的几何体可能是 ?.
17. 长方体是由 ? 个面围成,它有 ? 个顶点, ? 条棱.
18. 将如图几何体分类,柱体有 ?,锥 体 有 ?,球体有 ?(填序号).
19. 在正方体、长方体、球、圆柱、圆锥、三棱柱这些几何体中,不属于柱体的有 ?,属于四棱柱的有 ?.
20. 若一个直棱柱有 条棱,则这个直棱柱有 ? 个面.
21. 圆柱由 ? 个面围成,其中有 ? 个平面, ? 个曲面.
22. 一个棱柱有 个顶点,所有侧棱长的和是 ,则每条侧棱长是 ? .
23. 如图,六棱柱的底面边长都是 厘米,侧棱长为 厘米,则
()这个六棱柱一共有 ? 个面,有 ? 个顶点;
()这个六棱柱一共有 ? 条棱,它们的长度分别是 ?.
()顶点数 面数 棱数 ?.
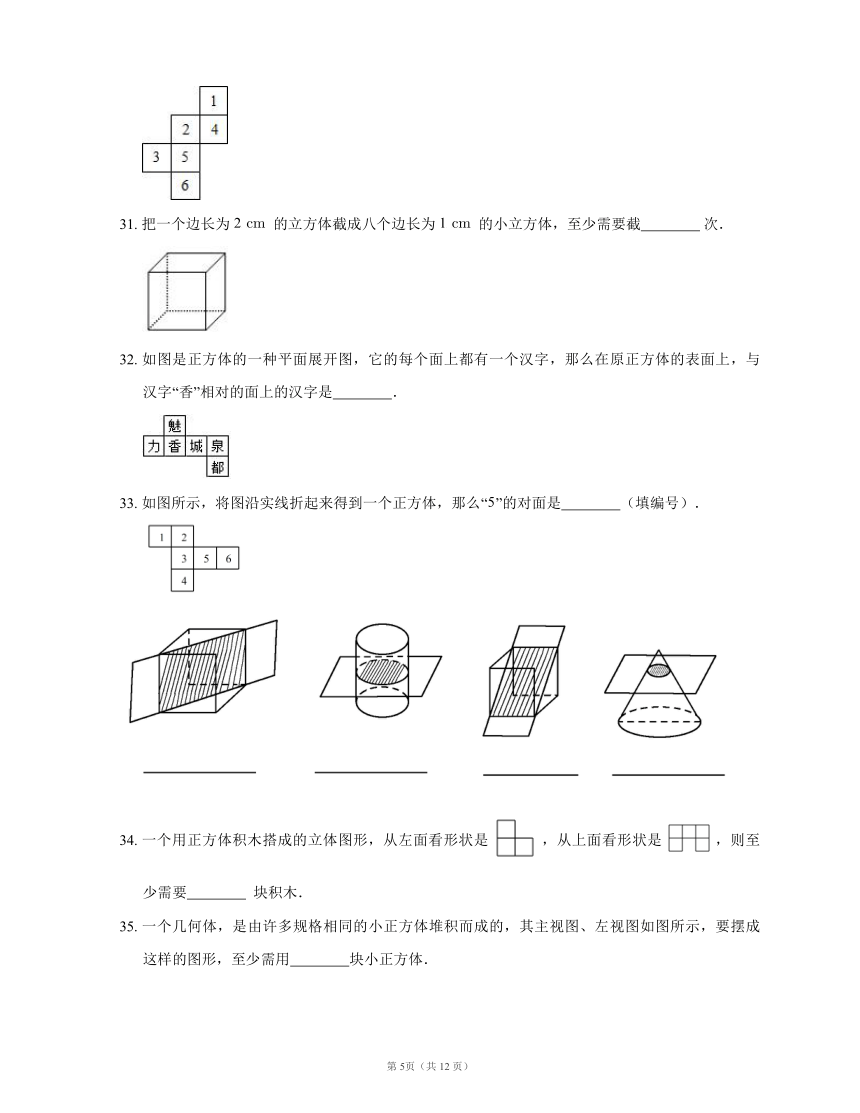
24. 如果用一个平面去截一个几何体,所得任意截面都是圆,则这个几何体是 ?.
25. 用平面去截一个几何体,如果截面是三角形,则这个几何体可能是 ?.
26. 由一些大小相同的小正方体组成的一个几何体的主视图和俯视图如图所示,那么组成该几何体所需的小正方体的个数最少为 ?.
27. 要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为 , ?, ?.
28. 如图,用一个平面分别截一个长方体、五棱柱,它们的截面形状分别是 ? 、 ?.
29. 有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动 算一次,则滚动第 次后,骰子朝下一面的点数是 ?.
30. 如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是 ?.
31. 把一个边长为 的立方体截成八个边长为 的小立方体,至少需要截 ? 次.
32. 如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“香”相对的面上的汉字是 ?.
33. 如图所示,将图沿实线折起来得到一个正方体,那么“”的对面是 ?(填编号).
34. 一个用正方体积木搭成的立体图形,从左面看形状是,从上面看形状是,则至少需要 ? 块积木.
35. 一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的图形,至少需用 ?块小正方体.
36. 如果按图中虚线对折可以做成一个上底面为无盖的盒子,那么该盒子的下底面的字母是 ?.
37. 如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“ ”相对的面上的数字是 ?.
38. 用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:① 正方体;② 圆柱;③ 圆锥;④ 正三棱柱 ?.(写出所有正确结果的序号).
39. 由若干个大小相同的小正方体搭成的几何体,从正面和从上面看到的形状图如图所示,则组成这个几何体的小正方体的个数最多是 ?.
40. 用一个平面截长方体、五棱柱、圆柱和圆锥,不能截出三角形的是 ?.
41. 如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要 ? 个小立方块.
42. 用八个同样大小的小立方体粘成一个大立方体如图 1,得到的几何体的三视图如图 2 所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图 2,则他取出的小立方体最多可以是 ?个.
43. 由几个相同小正方体搭成的几何体的主视图与左视图如图所示,则该几何体最少由 ? 个小正方体搭成.
44. 如图,在一次数学活动课上,张明用 个边长为 的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 ? 个小正方体,王亮所搭几何体表面积为 ?.
45. 如图所示是由若干个完全相同的小正方体搭成的几何体的主视图和俯视图.则这个几何体可能是由 ? 个正方体搭成的.
46. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其从三个不同方向看得到的平面图形中,面积最小的是从 ? 面看得到的平面图形.
47. 立方体木块的六个面分别标有数字 ,,,,,,下图是从不同方向观察这个立方体木块看到的数字情况,数字 和 对面的数字的和是 ?.
48. 马小虎准备制作一个封闭的正方体盒子,他先用 个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子(添加所有符合要求的正方形,添加的正方形用阴影表示) ?.
答案
1. 圆,长方形
2. ,,
3. 正方体,长方体,三棱柱,四棱锥,圆柱,圆柱,圆锥,三棱锥,三棱柱,三棱锥
4. 圆
5.
6. 真
7. 国
8. ③ ④ ② ① ⑤
9. 球,直六棱柱,圆锥,正方形,直三棱柱,圆柱,四棱锥,长方体
10. ②③
11. 羽毛球
12.
13. (),,,相同,(),,曲,(),
14. ③
15. 长方体,四棱锥,圆柱,圆锥,球
16. 正方体或圆
17. ,,
18. (),(),(),(),(),()
19. 球,圆锥,正方体,长方体
20.
21. ,,
22.
23. ,,,侧棱 ,底边 ,
24. 球
25. 圆锥、棱锥、棱柱等
26.
【解析】由主视图知几何体共两列,且左侧一列最高一层,右侧一列最高两层;
由俯视图可知左侧一行,右侧两行,于是可确定左侧只有一个小正方体,而右侧可能是一行单层一行两层,也可能两行都是两层,故小正方体最少有 个.
27. ,
28. 长方形,五边形
29.
【解析】观察图象知道点数三和点数四相对,点数二和点数五相对且四次一循环,
,
滚动第 次后与第二次相同,
朝下的点数为 .
30.
31.
【解析】上表面截两次中间截一次
32. 泉
33.
34.
【解析】根据从左面看的形状和从上面看的形状可得:
这个图形有 层,下层最少是 个正方体,上层至少 个正方形体,
则至少需要 块积木.
35.
36.
37.
38. ① ③ ④
39.
40. 圆柱
41.
【解析】由俯视图易得最底层有 个小立方体,第二层有 个小立方体,第三层有 个小立方体,那么共有 个几何体组成.
若搭成一个大正方体,共需 个小立方体,
所以还需 个小立方体.
42.
【解析】当如图所示摆放时剩余小正方体数最少.
43.
【解析】综合主视图和左视图可知,几何体的俯视图为三排三列,第一排最少在第三列放 个,第二排最少在第二列放 个,第三排最少在第一列放 个,故最少有 个小正方体.如图,数字表示该位置小正方体的个数.
44. ,
【解析】总共有小正方体 个,所以王亮还需要 个;
几何体的表面积为 .
45. 或 或
【解析】综合主视图和俯视图,这个几何体的底层有 个小正方体,
第二层最少有 个,最多有 个,
第三层最少有 个,最多有 个,
因此搭成这样的一个几何体至少需要小正方体木块的个数为: 个,
至多需要小正方体木块的个数为: 个,
即这个几何体可能是由 或 或 个正方体搭成的.
46. 左
47.
【解析】由图可知和 相邻的数字有 ,,,,
所以 对面的数字是 ,
而 不和 , 相对,
所以 的对面是 ,
所以 .
48.
1. 如图中的截面分别是() ?() ?.
2. 正方体或长方体是一个立体图形,它是由 ? 个面, ? 条棱, ? 个顶点组成的.
3. 分别写出表面能展开成如图所示的 个平面图形的几何体的名称.
4. 用平行于圆锥的底面的平面去截圆锥,则得到的截面是 ? 形.
5. 如图是六个棱长为 的小立方块组成的一个几何体,从上面看得到的图形的面积为 ?.
6. 如图,该图形经过折叠可以围成一个正方体,折好以后与“细”字相对的字是 ?.
7. 如图,是正方体的一个平面展开图,在这个正方体中,与“爱”字所在面相对的面上的汉字是 ?.
8. 如图1是一些具体物体的图形,分别是:三棱镜、方砖、笔筒、铅锤、粮囤,图2中是一些立体图形.在图1中找出与图2中立体图形类似的物体填人括号内.
9. 观察图中的立体图形,分别写出它们的名称.
10. 下列立体图形中,是柱体的是 ?.(填序号)
11. 篮球、排球、羽毛球、足球、乒乓球中,所呈现出的几何图形不是球的是 ?.
12. 如图,一个正四面体共有 个面、 个顶点、 ? 条棱.
13. ()正方体有 ? 个面, ? 个顶点, ? 条棱,这些棱的长度 ?;(填“相同”或“不同”)
()圆柱有 ? 个面,其中有 ? 个平面,还有一个面是 ? 面;
()若一个棱柱的底面是一个七边形,则它的侧面必须有 ? 个长方形,它一共有 ? 个面.
14. 下列图形中,都是柱体的一组是 ?.
15. 请在如图所示的横线上填写几何体的名称.
16. 从三个不同方向看都是同一平面图形的几何体可能是 ?.
17. 长方体是由 ? 个面围成,它有 ? 个顶点, ? 条棱.
18. 将如图几何体分类,柱体有 ?,锥 体 有 ?,球体有 ?(填序号).
19. 在正方体、长方体、球、圆柱、圆锥、三棱柱这些几何体中,不属于柱体的有 ?,属于四棱柱的有 ?.
20. 若一个直棱柱有 条棱,则这个直棱柱有 ? 个面.
21. 圆柱由 ? 个面围成,其中有 ? 个平面, ? 个曲面.
22. 一个棱柱有 个顶点,所有侧棱长的和是 ,则每条侧棱长是 ? .
23. 如图,六棱柱的底面边长都是 厘米,侧棱长为 厘米,则
()这个六棱柱一共有 ? 个面,有 ? 个顶点;
()这个六棱柱一共有 ? 条棱,它们的长度分别是 ?.
()顶点数 面数 棱数 ?.
24. 如果用一个平面去截一个几何体,所得任意截面都是圆,则这个几何体是 ?.
25. 用平面去截一个几何体,如果截面是三角形,则这个几何体可能是 ?.
26. 由一些大小相同的小正方体组成的一个几何体的主视图和俯视图如图所示,那么组成该几何体所需的小正方体的个数最少为 ?.
27. 要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为 , ?, ?.
28. 如图,用一个平面分别截一个长方体、五棱柱,它们的截面形状分别是 ? 、 ?.
29. 有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动 算一次,则滚动第 次后,骰子朝下一面的点数是 ?.
30. 如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是 ?.
31. 把一个边长为 的立方体截成八个边长为 的小立方体,至少需要截 ? 次.
32. 如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“香”相对的面上的汉字是 ?.
33. 如图所示,将图沿实线折起来得到一个正方体,那么“”的对面是 ?(填编号).
34. 一个用正方体积木搭成的立体图形,从左面看形状是,从上面看形状是,则至少需要 ? 块积木.
35. 一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的图形,至少需用 ?块小正方体.
36. 如果按图中虚线对折可以做成一个上底面为无盖的盒子,那么该盒子的下底面的字母是 ?.
37. 如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“ ”相对的面上的数字是 ?.
38. 用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:① 正方体;② 圆柱;③ 圆锥;④ 正三棱柱 ?.(写出所有正确结果的序号).
39. 由若干个大小相同的小正方体搭成的几何体,从正面和从上面看到的形状图如图所示,则组成这个几何体的小正方体的个数最多是 ?.
40. 用一个平面截长方体、五棱柱、圆柱和圆锥,不能截出三角形的是 ?.
41. 如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要 ? 个小立方块.
42. 用八个同样大小的小立方体粘成一个大立方体如图 1,得到的几何体的三视图如图 2 所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图 2,则他取出的小立方体最多可以是 ?个.
43. 由几个相同小正方体搭成的几何体的主视图与左视图如图所示,则该几何体最少由 ? 个小正方体搭成.
44. 如图,在一次数学活动课上,张明用 个边长为 的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 ? 个小正方体,王亮所搭几何体表面积为 ?.
45. 如图所示是由若干个完全相同的小正方体搭成的几何体的主视图和俯视图.则这个几何体可能是由 ? 个正方体搭成的.
46. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其从三个不同方向看得到的平面图形中,面积最小的是从 ? 面看得到的平面图形.
47. 立方体木块的六个面分别标有数字 ,,,,,,下图是从不同方向观察这个立方体木块看到的数字情况,数字 和 对面的数字的和是 ?.
48. 马小虎准备制作一个封闭的正方体盒子,他先用 个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子(添加所有符合要求的正方形,添加的正方形用阴影表示) ?.
答案
1. 圆,长方形
2. ,,
3. 正方体,长方体,三棱柱,四棱锥,圆柱,圆柱,圆锥,三棱锥,三棱柱,三棱锥
4. 圆
5.
6. 真
7. 国
8. ③ ④ ② ① ⑤
9. 球,直六棱柱,圆锥,正方形,直三棱柱,圆柱,四棱锥,长方体
10. ②③
11. 羽毛球
12.
13. (),,,相同,(),,曲,(),
14. ③
15. 长方体,四棱锥,圆柱,圆锥,球
16. 正方体或圆
17. ,,
18. (),(),(),(),(),()
19. 球,圆锥,正方体,长方体
20.
21. ,,
22.
23. ,,,侧棱 ,底边 ,
24. 球
25. 圆锥、棱锥、棱柱等
26.
【解析】由主视图知几何体共两列,且左侧一列最高一层,右侧一列最高两层;
由俯视图可知左侧一行,右侧两行,于是可确定左侧只有一个小正方体,而右侧可能是一行单层一行两层,也可能两行都是两层,故小正方体最少有 个.
27. ,
28. 长方形,五边形
29.
【解析】观察图象知道点数三和点数四相对,点数二和点数五相对且四次一循环,
,
滚动第 次后与第二次相同,
朝下的点数为 .
30.
31.
【解析】上表面截两次中间截一次
32. 泉
33.
34.
【解析】根据从左面看的形状和从上面看的形状可得:
这个图形有 层,下层最少是 个正方体,上层至少 个正方形体,
则至少需要 块积木.
35.
36.
37.
38. ① ③ ④
39.
40. 圆柱
41.
【解析】由俯视图易得最底层有 个小立方体,第二层有 个小立方体,第三层有 个小立方体,那么共有 个几何体组成.
若搭成一个大正方体,共需 个小立方体,
所以还需 个小立方体.
42.
【解析】当如图所示摆放时剩余小正方体数最少.
43.
【解析】综合主视图和左视图可知,几何体的俯视图为三排三列,第一排最少在第三列放 个,第二排最少在第二列放 个,第三排最少在第一列放 个,故最少有 个小正方体.如图,数字表示该位置小正方体的个数.
44. ,
【解析】总共有小正方体 个,所以王亮还需要 个;
几何体的表面积为 .
45. 或 或
【解析】综合主视图和俯视图,这个几何体的底层有 个小正方体,
第二层最少有 个,最多有 个,
第三层最少有 个,最多有 个,
因此搭成这样的一个几何体至少需要小正方体木块的个数为: 个,
至多需要小正方体木块的个数为: 个,
即这个几何体可能是由 或 或 个正方体搭成的.
46. 左
47.
【解析】由图可知和 相邻的数字有 ,,,,
所以 对面的数字是 ,
而 不和 , 相对,
所以 的对面是 ,
所以 .
48.
