第一章丰富的图形世界 解答题练习(含答案)
文档属性
| 名称 | 第一章丰富的图形世界 解答题练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-01 00:00:00 | ||
图片预览


文档简介
丰富的图形世界解答题练习
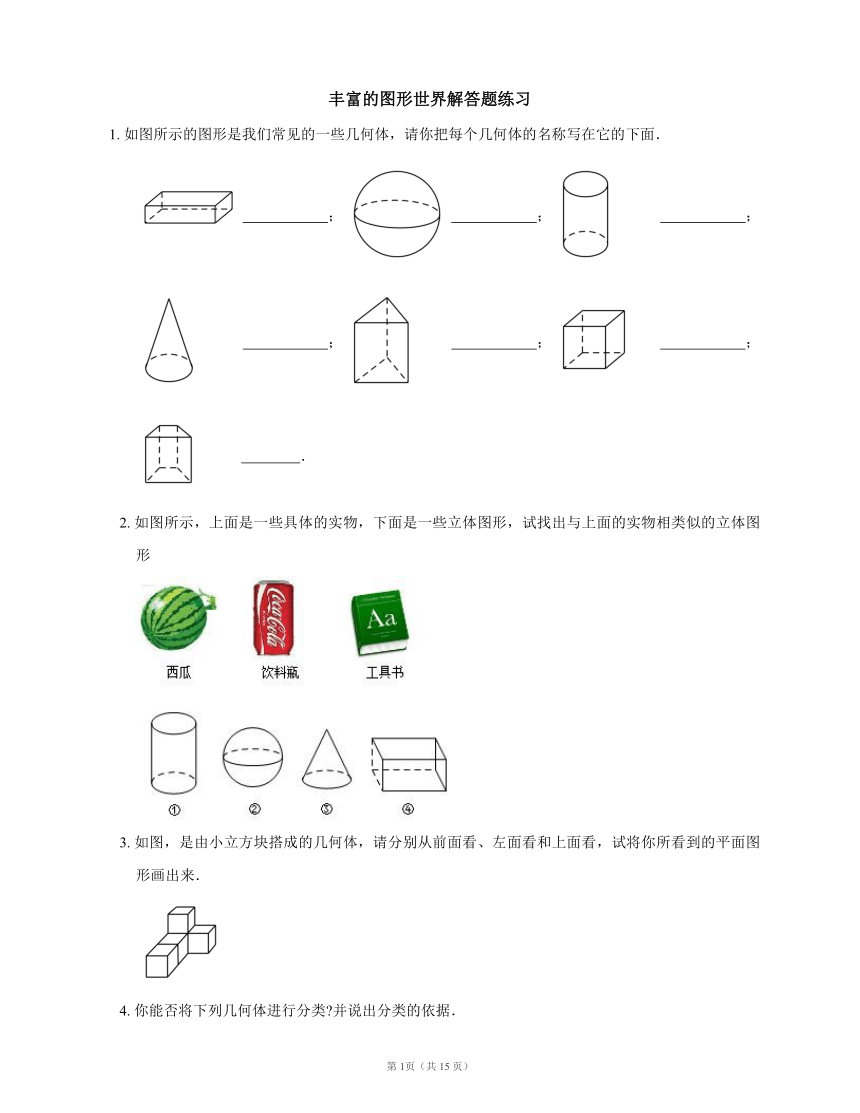
1. 如图所示的图形是我们常见的一些几何体,请你把每个几何体的名称写在它的下面.
?; ?; ?; ?; ?; ?; ?.
2. 如图所示,上面是一些具体的实物,下面是一些立体图形,试找出与上面的实物相类似的立体图形
3. 如图,是由小立方块搭成的几何体,请分别从前面看、左面看和上面看,试将你所看到的平面图形画出来.
4. 你能否将下列几何体进行分类?并说出分类的依据.
5. 如图所示,上面是一些具体的物体,下面是一些立体图形,试找出与下面的立体图形相类似的实物.
6. 如图所示,请将下列几何体分类.
7. 如图,有一个几何体,请画出从不同方向看它的平面图形.
()从正面看;
()从左面看;
()从上面看.
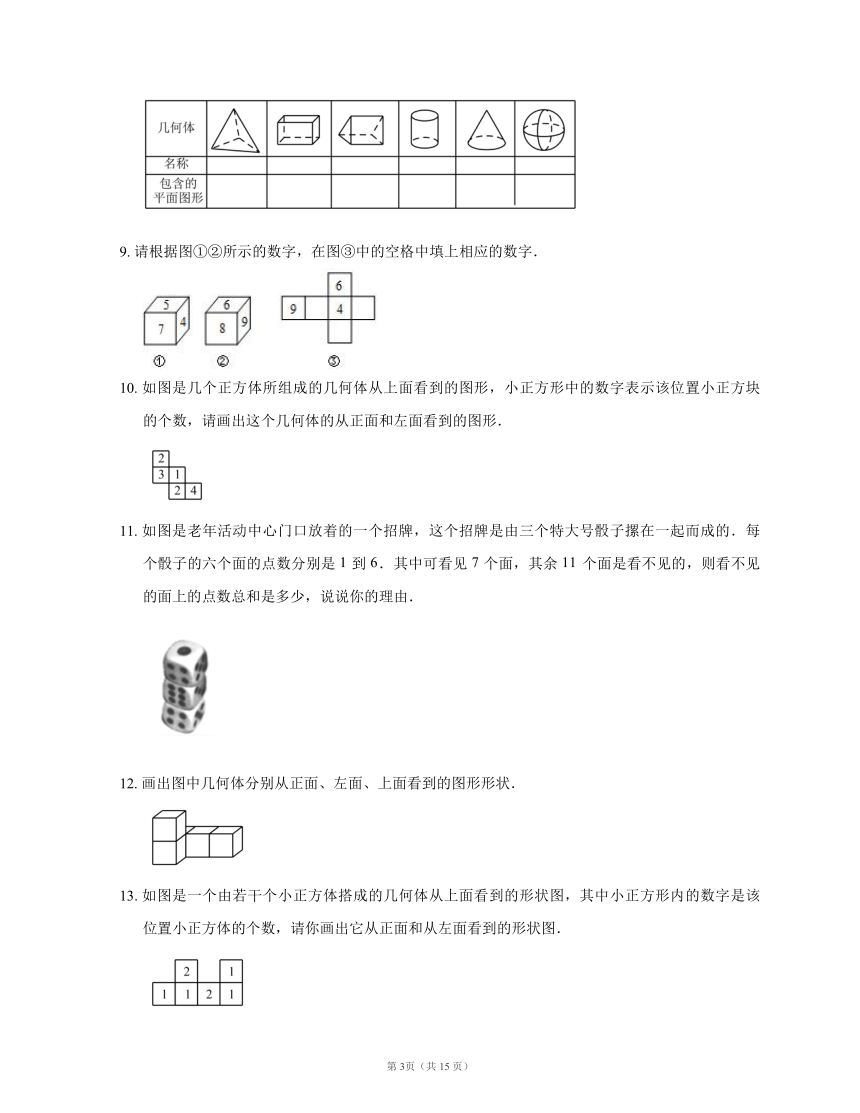
8. 请根据要求完成下表:
9. 请根据图①②所示的数字,在图③中的空格中填上相应的数字.
10. 如图是几个正方体所组成的几何体从上面看到的图形,小正方形中的数字表示该位置小正方块的个数,请画出这个几何体的从正面和左面看到的图形.
11. 如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号骰子摞在一起而成的.每个骰子的六个面的点数分别是 到 .其中可看见 个面,其余 个面是看不见的,则看不见的面上的点数总和是多少,说说你的理由.
12. 画出图中几何体分别从正面、左面、上面看到的图形形状.
13. 如图是一个由若干个小正方体搭成的几何体从上面看到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出它从正面和从左面看到的形状图.
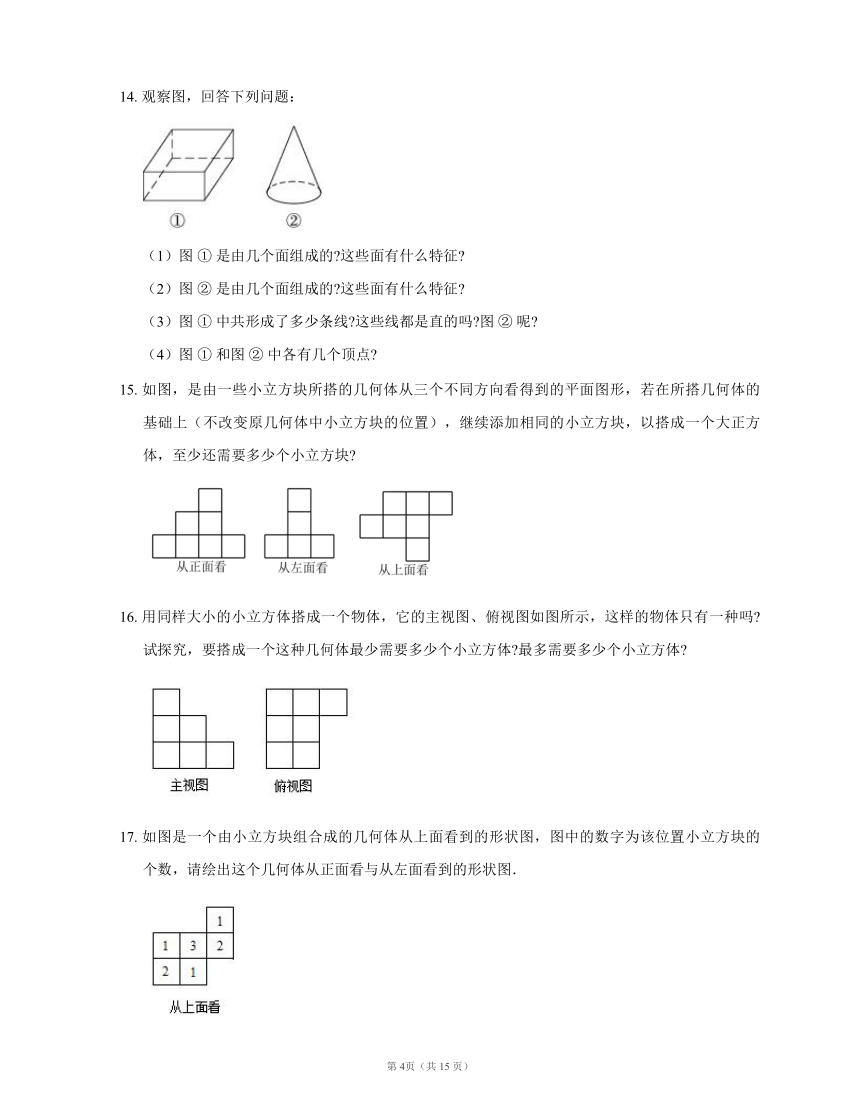
14. 观察图,回答下列问题:
(1)图 ① 是由几个面组成的?这些面有什么特征?
(2)图 ② 是由几个面组成的?这些面有什么特征?
(3)图 ① 中共形成了多少条线?这些线都是直的吗?图 ② 呢?
(4)图 ① 和图 ② 中各有几个顶点?
15. 如图,是由一些小立方块所搭的几何体从三个不同方向看得到的平面图形,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要多少个小立方块?
16. 用同样大小的小立方体搭成一个物体,它的主视图、俯视图如图所示,这样的物体只有一种吗?试探究,要搭成一个这种几何体最少需要多少个小立方体?最多需要多少个小立方体?
17. 如图是一个由小立方块组合成的几何体从上面看到的形状图,图中的数字为该位置小立方块的个数,请绘出这个几何体从正面看与从左面看到的形状图.
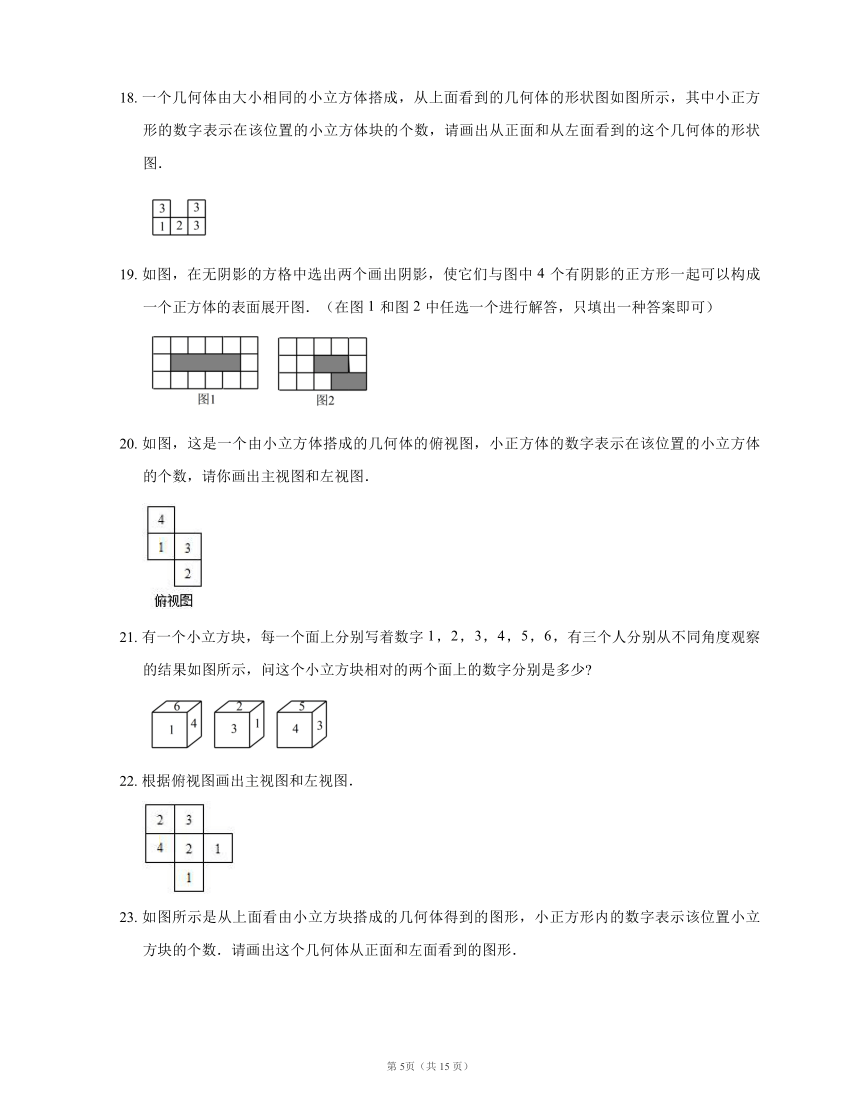
18. 一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形的数字表示在该位置的小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.
19. 如图,在无阴影的方格中选出两个画出阴影,使它们与图中 个有阴影的正方形一起可以构成一个正方体的表面展开图.(在图 和图 中任选一个进行解答,只填出一种答案即可)
20. 如图,这是一个由小立方体搭成的几何体的俯视图,小正方体的数字表示在该位置的小立方体的个数,请你画出主视图和左视图.
21. 有一个小立方块,每一个面上分别写着数字 ,,,,,,有三个人分别从不同角度观察的结果如图所示,问这个小立方块相对的两个面上的数字分别是多少?
22. 根据俯视图画出主视图和左视图.
23. 如图所示是从上面看由小立方块搭成的几何体得到的图形,小正方形内的数字表示该位置小立方块的个数.请画出这个几何体从正面和左面看到的图形.
24. 如图,在 的方格中,取适当的 个小正方形折叠成一个无盖的正方体盒子,在图中设计出一种方案.
25. 如图,第 行是一些具体的物体,第 行是一些立体图形,试找出与第 行立体图形相类似的实物(用线连接).
26. 请写出下列几何体的名称.
(1) ? (2) ? (3) ? (4) ? (5) ? (6) ?
27. 用小立方块搭一个几何体,使它从正面和从上面看的形状图如图所示.从上面看的形状图中,小正方形中的字母表示该位置小立方块的个数,试回答下列问题.
(1), 各表示多少?
(2) 可能是多少?这个几何体最少由几个小立方块搭成?最多呢?
28. 把立方体的 个面分别涂上 种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况列表如下:
现将和上述大小相同、花朵颜色分布完全一样的 个立方体拼成一个水平放置的长方体,如图所示,那么此长方体的下底面有多少朵花?试写出你的结论,并说出推理过程.
29. 如图中的一些积木是由 块棱长为 的正方体堆成的,它的表面积是多少平方厘米?
30. 根据下面的俯视图,其搭建的每一正方体边长为 ,画出它的主视图和左视图,并求其表面积.
31. 如图是一些小正方体搭成的几何体俯视图,小正方形中的数字表示该位置的小正方体的个数,请画出它的主视图,左视图.
32. 某学校设计了如图所示的一个雕塑,取名为"阶梯".现在打算用油漆喷刷所有暴露面,经测量,每个小立方块的棱长为 米.请计算需喷油漆的总面积是多少?
33. 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
34. 如图所示是由几个小立方块搭成的几何体从上面看的形状图,请画出这个几何体从正面和从左面看的形状图.
35. 如图所示是一个正方体的表面展开图,把 ,,,,, 分别填入 个小正方形内,使得按虚线折成正方体后相对的两个面上的数字之和为 ,尝试不同的填法,并与同学交流.
36. 图中是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的主视图和左视图.
答案
1. 长方体;球;圆柱;圆锥;三棱柱;正方体;四棱柱
2. 西瓜 (2)球;饮料瓶 (1)圆柱;工具书 (4)长方体.
3.
4. 答案不唯一,如按柱体、锥体、球分,柱体有:①③④⑤⑥⑧,锥体有:②,球有:⑦.
5. 埃及金字塔 (2)三棱锥;西瓜 (3)球;北京天坛 (4)圆锥;书本 (5)长方体.
6. 方法一:(1)、(3)、(5)是一类,都是柱体;(2)是锥体,(4)是球体.
方法二:(1)、(3)是一类,全是由平面构成的;(2)、(5)是一类,既有平面,又有曲面.(4)是一类,只有曲面.
7.
8.
9. 对面是 , 对面是 ( 在 与 之间), 对面是 .
【解析】可以自己用纸剪一个试试看.
10. 如图,主视图及左视图如下:
11. 看不见的面上的点数和为 .理由如下:
一个正方体般子有六个面,点数和为 ,
共有 个正方体骰子,点数和为 .
观察题图可知能看见 个面的点数和为 ,
所以看不见的面上的点数和为 .
12. 如图所示:
从正面看
从左面看
从上面看
13. 作图
14. (1) 图 ① 是由 个面组成的,这些面都是平的.
??????(2) 图 ② 是由 个面组成的, 个平的面和 个曲的面.
??????(3) 图 ① 中共形成了 条线,这些线都是直的;
图 ② 中形成了 条线,是曲线.
??????(4) 图 ① 中有 个顶点;
图 ② 中只有 个顶点.
15. .
16. 这样的物体不只一种.
搭成这样的几何体最少需要小立方体的个数是:
(个);
最多需要小立方体的个数是:(个).
17.
18. 作图如下:
19. 只写出一种答案即可.
20. 如图:
21. 从 个小立方体上的数可知,与写有数字 的面相邻的面上数字是 ,,,,
数字 面对数字 面,
同理,立方体面上数字 对 ,
故立方体面上数字 对 .
22. 如图所示:
23.
24. 如图所示(答案不唯一).
25.
26. (1)正方体;(2)球;(3)圆柱;(4)长方体;(5)圆锥;(6)三棱柱
27. (1) ,.
??????(2) 可能是 或 ,
,
.
这个几何体最少由 个立方体搭成,最多由 个立方体搭成.
28. 该立方体的红对绿,黄对紫,蓝对白,
所以长方体的下底面的花朵的朵数为 (朵).
29. 上面和下面的面积为 ;
前面和后面的面积为 ;
两个侧面的面积为 ;
中间缺口处还有 个面,其面积为 .
因为 ,所以这个几何体的表面积为 .
30. 如图即为所求.
表面积为 .
31. 如图所示:
32. 画出雕塑"阶梯"的形状图,如图所示.
每个小正方形的面积都是 (平方米),
所以喷漆总面积为 (平方米).
答:需喷油漆的总面积为 平方米.
33.
34.
35. (答案不唯一)
36. 如图所示:
1. 如图所示的图形是我们常见的一些几何体,请你把每个几何体的名称写在它的下面.
?; ?; ?; ?; ?; ?; ?.
2. 如图所示,上面是一些具体的实物,下面是一些立体图形,试找出与上面的实物相类似的立体图形
3. 如图,是由小立方块搭成的几何体,请分别从前面看、左面看和上面看,试将你所看到的平面图形画出来.
4. 你能否将下列几何体进行分类?并说出分类的依据.
5. 如图所示,上面是一些具体的物体,下面是一些立体图形,试找出与下面的立体图形相类似的实物.
6. 如图所示,请将下列几何体分类.
7. 如图,有一个几何体,请画出从不同方向看它的平面图形.
()从正面看;
()从左面看;
()从上面看.
8. 请根据要求完成下表:
9. 请根据图①②所示的数字,在图③中的空格中填上相应的数字.
10. 如图是几个正方体所组成的几何体从上面看到的图形,小正方形中的数字表示该位置小正方块的个数,请画出这个几何体的从正面和左面看到的图形.
11. 如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号骰子摞在一起而成的.每个骰子的六个面的点数分别是 到 .其中可看见 个面,其余 个面是看不见的,则看不见的面上的点数总和是多少,说说你的理由.
12. 画出图中几何体分别从正面、左面、上面看到的图形形状.
13. 如图是一个由若干个小正方体搭成的几何体从上面看到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出它从正面和从左面看到的形状图.
14. 观察图,回答下列问题:
(1)图 ① 是由几个面组成的?这些面有什么特征?
(2)图 ② 是由几个面组成的?这些面有什么特征?
(3)图 ① 中共形成了多少条线?这些线都是直的吗?图 ② 呢?
(4)图 ① 和图 ② 中各有几个顶点?
15. 如图,是由一些小立方块所搭的几何体从三个不同方向看得到的平面图形,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要多少个小立方块?
16. 用同样大小的小立方体搭成一个物体,它的主视图、俯视图如图所示,这样的物体只有一种吗?试探究,要搭成一个这种几何体最少需要多少个小立方体?最多需要多少个小立方体?
17. 如图是一个由小立方块组合成的几何体从上面看到的形状图,图中的数字为该位置小立方块的个数,请绘出这个几何体从正面看与从左面看到的形状图.
18. 一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形的数字表示在该位置的小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.
19. 如图,在无阴影的方格中选出两个画出阴影,使它们与图中 个有阴影的正方形一起可以构成一个正方体的表面展开图.(在图 和图 中任选一个进行解答,只填出一种答案即可)
20. 如图,这是一个由小立方体搭成的几何体的俯视图,小正方体的数字表示在该位置的小立方体的个数,请你画出主视图和左视图.
21. 有一个小立方块,每一个面上分别写着数字 ,,,,,,有三个人分别从不同角度观察的结果如图所示,问这个小立方块相对的两个面上的数字分别是多少?
22. 根据俯视图画出主视图和左视图.
23. 如图所示是从上面看由小立方块搭成的几何体得到的图形,小正方形内的数字表示该位置小立方块的个数.请画出这个几何体从正面和左面看到的图形.
24. 如图,在 的方格中,取适当的 个小正方形折叠成一个无盖的正方体盒子,在图中设计出一种方案.
25. 如图,第 行是一些具体的物体,第 行是一些立体图形,试找出与第 行立体图形相类似的实物(用线连接).
26. 请写出下列几何体的名称.
(1) ? (2) ? (3) ? (4) ? (5) ? (6) ?
27. 用小立方块搭一个几何体,使它从正面和从上面看的形状图如图所示.从上面看的形状图中,小正方形中的字母表示该位置小立方块的个数,试回答下列问题.
(1), 各表示多少?
(2) 可能是多少?这个几何体最少由几个小立方块搭成?最多呢?
28. 把立方体的 个面分别涂上 种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况列表如下:
现将和上述大小相同、花朵颜色分布完全一样的 个立方体拼成一个水平放置的长方体,如图所示,那么此长方体的下底面有多少朵花?试写出你的结论,并说出推理过程.
29. 如图中的一些积木是由 块棱长为 的正方体堆成的,它的表面积是多少平方厘米?
30. 根据下面的俯视图,其搭建的每一正方体边长为 ,画出它的主视图和左视图,并求其表面积.
31. 如图是一些小正方体搭成的几何体俯视图,小正方形中的数字表示该位置的小正方体的个数,请画出它的主视图,左视图.
32. 某学校设计了如图所示的一个雕塑,取名为"阶梯".现在打算用油漆喷刷所有暴露面,经测量,每个小立方块的棱长为 米.请计算需喷油漆的总面积是多少?
33. 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
34. 如图所示是由几个小立方块搭成的几何体从上面看的形状图,请画出这个几何体从正面和从左面看的形状图.
35. 如图所示是一个正方体的表面展开图,把 ,,,,, 分别填入 个小正方形内,使得按虚线折成正方体后相对的两个面上的数字之和为 ,尝试不同的填法,并与同学交流.
36. 图中是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的主视图和左视图.
答案
1. 长方体;球;圆柱;圆锥;三棱柱;正方体;四棱柱
2. 西瓜 (2)球;饮料瓶 (1)圆柱;工具书 (4)长方体.
3.
4. 答案不唯一,如按柱体、锥体、球分,柱体有:①③④⑤⑥⑧,锥体有:②,球有:⑦.
5. 埃及金字塔 (2)三棱锥;西瓜 (3)球;北京天坛 (4)圆锥;书本 (5)长方体.
6. 方法一:(1)、(3)、(5)是一类,都是柱体;(2)是锥体,(4)是球体.
方法二:(1)、(3)是一类,全是由平面构成的;(2)、(5)是一类,既有平面,又有曲面.(4)是一类,只有曲面.
7.
8.
9. 对面是 , 对面是 ( 在 与 之间), 对面是 .
【解析】可以自己用纸剪一个试试看.
10. 如图,主视图及左视图如下:
11. 看不见的面上的点数和为 .理由如下:
一个正方体般子有六个面,点数和为 ,
共有 个正方体骰子,点数和为 .
观察题图可知能看见 个面的点数和为 ,
所以看不见的面上的点数和为 .
12. 如图所示:
从正面看
从左面看
从上面看
13. 作图
14. (1) 图 ① 是由 个面组成的,这些面都是平的.
??????(2) 图 ② 是由 个面组成的, 个平的面和 个曲的面.
??????(3) 图 ① 中共形成了 条线,这些线都是直的;
图 ② 中形成了 条线,是曲线.
??????(4) 图 ① 中有 个顶点;
图 ② 中只有 个顶点.
15. .
16. 这样的物体不只一种.
搭成这样的几何体最少需要小立方体的个数是:
(个);
最多需要小立方体的个数是:(个).
17.
18. 作图如下:
19. 只写出一种答案即可.
20. 如图:
21. 从 个小立方体上的数可知,与写有数字 的面相邻的面上数字是 ,,,,
数字 面对数字 面,
同理,立方体面上数字 对 ,
故立方体面上数字 对 .
22. 如图所示:
23.
24. 如图所示(答案不唯一).
25.
26. (1)正方体;(2)球;(3)圆柱;(4)长方体;(5)圆锥;(6)三棱柱
27. (1) ,.
??????(2) 可能是 或 ,
,
.
这个几何体最少由 个立方体搭成,最多由 个立方体搭成.
28. 该立方体的红对绿,黄对紫,蓝对白,
所以长方体的下底面的花朵的朵数为 (朵).
29. 上面和下面的面积为 ;
前面和后面的面积为 ;
两个侧面的面积为 ;
中间缺口处还有 个面,其面积为 .
因为 ,所以这个几何体的表面积为 .
30. 如图即为所求.
表面积为 .
31. 如图所示:
32. 画出雕塑"阶梯"的形状图,如图所示.
每个小正方形的面积都是 (平方米),
所以喷漆总面积为 (平方米).
答:需喷油漆的总面积为 平方米.
33.
34.
35. (答案不唯一)
36. 如图所示:
