2.6.1 应用一元二次方程同步作业

21世纪教育网 –中小学教育资源及组卷应用平台
2.6.1应用一元二次方程同步作业
姓名：__________班级：__________考号：__________
一 、选择题（本大题共8小题 ）
已知△ABC是等腰三角形，BC=8，AB， AC的长是关于x的一元二次方程x2-10x+k=0的两根，则（　　）
A、k=16 B、k=25 C、k=-16或k=-25 D、k=16或k=25
如图，将边长为2cm的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，若两个三角形重叠部分的面积为1cm2 ， 则它移动的距离AA′等于（　　）
A、0.5cm B、1cm C、1.5cm D、2cm
现有一块长方形绿地，它的短边长为20 m，若将短边增大到与长边相等(长边不变)，使扩大后的绿地的形状是正方形，则扩大后的绿地面积比原来增加300 m2，设扩大后的正方形绿地边长为xm，下面所列方程正确的是( )
A. x(x-20)=300 B. x(x+20)=300 C. 60(x+20)=300 D. 60(x-20)=300
一个等腰三角形的两条边长分别是方程x2-3x+2=0的两根，则该等腰三角形的周长是( )
A. 5或4 B. 4 C. 5 D. 3
如图，AB⊥BC，AB＝10 cm，BC＝8 cm，一只蝉从C点沿CB方向以每秒1 cm的速度爬行，蝉开始爬行的同时，一只螳螂由A点沿AB方向以每秒2 cm的速度爬行，当螳螂和蝉爬行x秒后，它们分别到达了M，N的位置，此时，△MNB的面积恰好为24 cm2，由题意可列方程(　　)
A. 2x·x＝24 B. (10－2x)(8－x)＝24
C. (10－x)(8－2x)＝24 D. (10－2x)(8－x)＝48
有一块长方形铁皮，长100cm，宽50cm，在它的四周各切去一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒．如果要制作的无盖方盒的底面积为3600cm2，设铁皮各角应切去的正方形边长为xcm，则下面所列方程正确的是（　　）
A．4x2=3600 B．100×50﹣4x2=3600
C．（100﹣x）（50﹣x）=3600 D．（100﹣2x）（50﹣2x）=3600
把一个正方形的一边增加2cm，另一边增加1cm，所得的长方形的面积比正方形面积增加14cm2，那么原来正方形的边长是（　　）
A． 3cm B． 5cm C． 4cm D． 6cm
如图，点E在正方形ABCD的边AD上，已知AE=7，CE=13，则阴影部分的面积是（　　）
A.114 B.124 C.134 D.144
二、填空题（本大题共6小题 ）
如图，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G．若图中阴影部分的面积与正方形ABCD的面积之比为2：3，则△BCG的周长为　 　．
如图，某小区规划在一个长为16m、宽为9m的矩形场地ABCD上修建三条同样宽的小路，使其中两条与AB平行，另一条与AD平行，其余部分种草．若草坪部分的总面积为112m2，求小路的宽度．若设小路的宽度为xm，则x满足的方程为__________________．
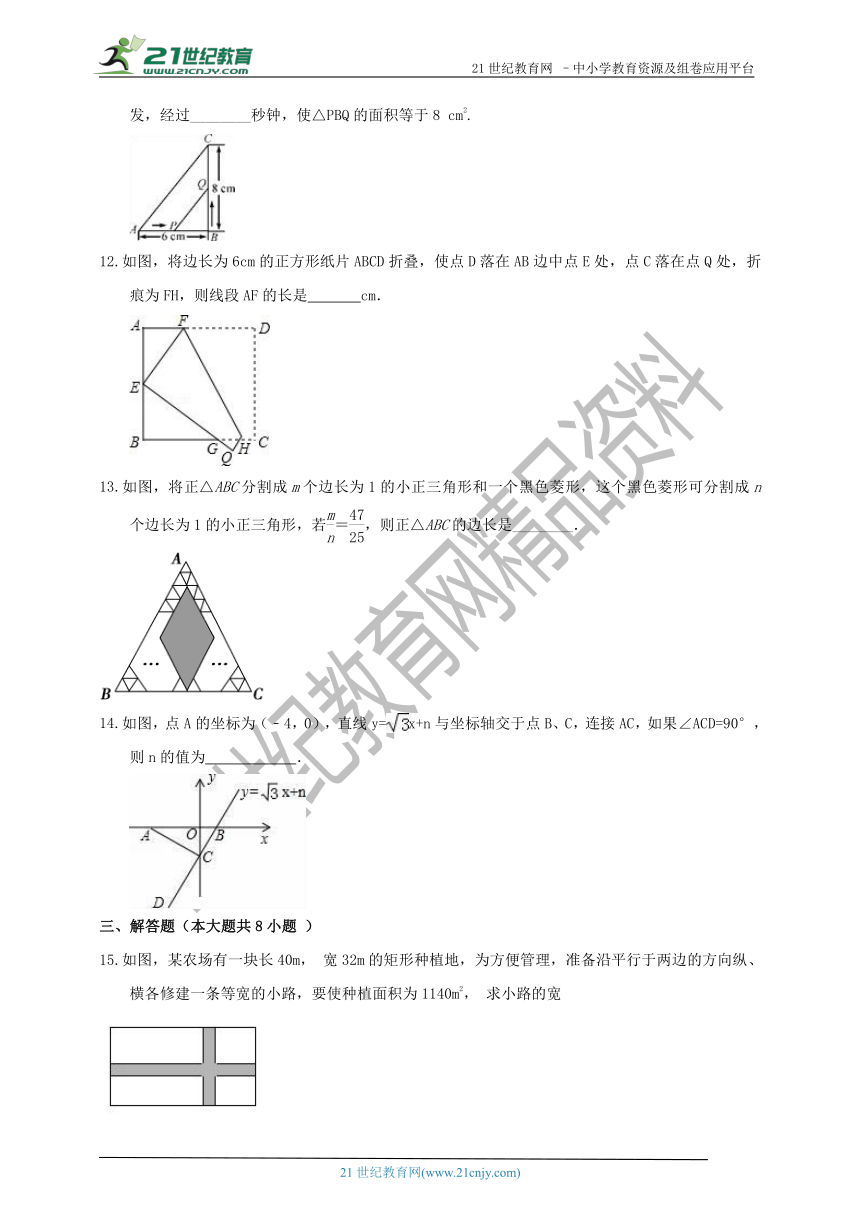
如图，在Rt△ABC中，∠B＝90°，AB＝6 cm，BC＝8 cm，点P从A点开始沿AB边向点B以1 cm/s的速度移动，点Q从B点开始沿BC边向点C以2 cm/s的速度移动，则P、Q分别从A、B同时出发，经过________秒钟，使△PBQ的面积等于8 cm2.
如图，将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长是　 　cm．
如图，将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形，这个黑色菱形可分割成n个边长为1的小正三角形，若＝，则正△ABC的边长是________．
如图，点A的坐标为（﹣4，0），直线y=x+n与坐标轴交于点B、C，连接AC，如果∠ACD=90°，则n的值为　　　　　　．
三、解答题（本大题共8小题 ）
如图，某农场有一块长40m， 宽32m的矩形种植地，为方便管理，准备沿平行于两边的方向纵、横各修建一条等宽的小路，要使种植面积为1140m2， 求小路的宽
如图，在Rt△ABC中，AC=24cm，BC=7cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5cm/s．若点P、Q分别从B、C同时运动，且运动时间记为t秒，请解答下面的问题，并写出探索的主要过程．
（1）当t为何值时，P、Q两点的距离为5cm？
（2）当t为何值时，△PCQ的面积为15cm2？
（3）请用配方法说明，点P运动多少时间时，四边形BPQA的面积最小？最小面积是多少？
如图，等边三角形ABC的边长为6cm，点P自点B出发，以1cm/s的速度向终点C运动；点Q自点C出发，以1cm/s的速度向终点A运动．若P，Q两点分别同时从B，C两点出发，问经过多少时间△PCQ的面积是2cm2？
在直角墙角AOB（OA⊥OB，且OA、OB长度不限）中，要砌20m长的墙，与直角墙角AOB围成地面为矩形的储仓，且地面矩形AOBC的面积为96m2．
（1）求这地面矩形的长；
（2）有规格为0.80×0.80和1.00×1.00（单位：m）的地板砖单价分别为55元/块和80元/块，若只选其中一种地板砖都恰好能铺满储仓的矩形地面（不计缝隙），用哪一种规格的地板砖费用较少？
如图所示，△ABC中，∠B=90°，AB=6cm，BC=8cm．点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发，
（1）如果P、Q同时出发，几秒后，可使△PBQ的面积为8平方厘米？
（2）线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能说明理由．
如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根．
（1）求C点坐标；
（2）求直线MN的解析式；
（3）在直线MN上存在点P，使以点P，B，C三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．
已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．
（1）如图①，当∠MAN点A旋转到BM=DN时，请你直接写出AH与AB的数量关系：　　　　　　；
（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；
（3）如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长．（可利用（2）得到的结论）
答案解析
一 、选择题
【考点】一元二次方程的应用
【分析】根据当BC是腰，则AB或AC有一个是8，进而得出k的值，再利用当BC是底，则AB和AC是腰，再利用根的判别式求出即可
解：当BC是腰，则AB或AC有一个是8，故82-10×8+k=0，
解得：k=-16，
当BC是底，则AB和AC是腰，则b2-4ac=102-4×1×k=100-4k=0，
解得：k=-25，
综上所述：k=-16或k=-25．
故选：C．
【考点】一元二次方程的应用，平行四边形的性质，正方形的性质，平移的性质
【分析】根据平移的性质，结合阴影部分是平行四边形，△AA′H与△HCB′都是等腰直角三角形，则若设AA′=x ， 则阴影部分的底长为x ， 高A′D=2-x ， 根据平行四边形的面积公式即可列出方程求解 解: 设AC交A′B′于H ，
∵∠A=45°，∠D=90°
∴△A′HA是等腰直角三角形
设AA′=x ， 则阴影部分的底长为x ， 高A′D=2-x
∴x （2-x）=1
∴x=1
即AA′=1cm ．
故选B．
A
【解析】分析：设扩大后的正方形绿地边长为xm，根据“扩大后的绿地面积比原来增加300m2”建立方程即可．
详解：设扩大后的正方形绿地边长为xm，根据题意得
x2-20x=300，
即x（x-20）=300．
故选A．
点睛： 本题考查了由实际问题抽象出一元二次方程，解题的关键是弄清题意，并找到等量关系．
C
【解析】试题解析：（x-1）（x-2）=0，
x-1=0或x-2=0，
所以x1=1，x2=2，
因为1+1=2，
所以三角形三边的长为2、2、1，
所以三角形的周长为5．
故选C．
D
【解析】设x秒后，螳螂走了 2x,蝉走了x,MB=10-2x,NC=8-x,
由题意知 (10－2x)(8－x)＝24,
(10－2x)(8－x)＝48,选D.
【考点】由实际问题抽象出一元二次方程．
【分析】易得底面积的长=原来的长﹣2×切去的正方形的边长，宽=原来的宽﹣2×切去的正方形的边长，根据长×宽=3600列方程即可．
解：设切去的小正方形的边长为x．
根据题意得（100﹣2x）（50﹣2x）=3600．
故选D．
【点评】考查一元二次方程的应用；得到无盖方盒的底面积的边长是解决本题的突破点．
【考点】一元二次方程的应用．
【分析】本题的等量关系是：长方形的面积=正方形面积+14cm2，根据这个等量关系列出方程．
解：设原来正方形的边长为xcm．
根据题意，可列方程为（x+2）（x+1）=x2+14，
经解和检验后得x=4．
即：原来正方形的边长为4cm．
故选：C．
点评： 本题考查了一元二次方程的应用．对于面积问题应熟记各种图形的面积公式．长方形的面积=长×宽，正方形的面积=边长×边长．
【考点】正方形的性质．
【分析】 由正方形的性质得出∠D=90°，AB=BC=AD，设AB=BC=AD=x，则DE=x﹣7，根据勾股定理得出CD2+DE2=CE2，得出方程x2+（x﹣7）2=132，解方程求出BC=AB=12，即可得出阴影部分的面积=（AE+BC） AB．
解：∵四边形ABCD是正方形，
∴∠D=90°，AB=BC=AD，
设AB=BC=AD=x，
则DE=x﹣7，
∵CD2+DE2=CE2，
∴x2+（x﹣7）2=132，
解得：x=12，或x=﹣5（不合题意，舍去），
∴BC=AB=12，
∴阴影部分的面积=（AE+BC） AB=×（7+12）×12=114；
故选：A．
点评： 本题考查了正方形的性质、勾股定理、以及梯形面积的计算；熟练掌握正方形的性质，并能进行推理计算是解决问题的关键．
二 、填空题
【考点】全等三角形的判定与性质，正方形的性质，三角形面积
【分析】根据面积之比得出△BGC的面积等于正方形面积的，进而依据△BCG的面积以及勾股定理，得出BG+CG的长，进而得出其周长．
解：∵阴影部分的面积与正方形ABCD的面积之比为2：3，
∴阴影部分的面积为×9=6，
∴空白部分的面积为9﹣6=3，
由CE=DF，BC=CD，∠BCE=∠CDF=90°，可得△BCE≌△CDF，
∴△BCG的面积与四边形DEGF的面积相等，均为×3=，
设BG=a，CG=b，则ab=，
又∵a2+b2=32，
∴a2+2ab+b2=9+6=15，
即（a+b）2=15，
∴a+b=，即BG+CG=，
∴△BCG的周长=+3，
故答案为：+3．
【点评】此题考查了全等三角形的判定与性质、正方形的性质以及三角形面积问题．解题时注意数形结合思想与方程思想的应用．
（16－2x)(9－x)＝112
【解析】设小路的宽度为xm，
那么草坪的总长度和总宽度应该为16-2x，9-x，
根据题意即可得出方程为：（16-2x）（9-x）=112，
故答案为：（16-2x）（9-x）=112.
2或4
【解析】设x秒时．由三角形的面积公式列出关于x的方程，
（6-x） 2x=8，
通过解方程求得x1=2，x2=4；
故答案为2或4.
【考点】翻折变换（折叠问题）；正方形的性质．一元二次方程的应用
【分析】设EF=FD=x，在RT△AEF中利用勾股定理即可解决问题．
解：如图：
∵四边形ABCD是正方形，
∴AB=BC=CD=AD=6，
∵AE=EB=3，EF=FD，设EF=DF=x．则AF=6﹣x，
在RT△AEF中，∵AE2+AF2=EF2，
∴32+（6﹣x）2=x2，
∴x=，
∴AF=6﹣=cm，
故答案为．
解：设正△ABC的边长为x，则高为x，S△ABC＝x·x＝x2.∵所分成的都是正三角形，
∴结合图形可得黑色菱形的较长的对角线为x－，
较短的对角线为(x－)＝x－1，
∴黑色菱形的面积＝＝(x－2)2，
∴＝＝，
整理得，11x2－144x＋144＝0，解得x1＝(不符合题意，舍去)，x2＝12.∴△ABC的边长是12.
答案　12
【考点】一次函数图象上点的坐标特征．
【分析】由直线y=x+n与坐标轴交于点B，C，得B点的坐标为（﹣n，0），C点的坐标为（0，n），由A点的坐标为（﹣4，0），∠ACD=90°，用勾股定理列出方程求出n的值．
解：∵直线y=x+n与坐标轴交于点B，C，
∴B点的坐标为（﹣n，0），C点的坐标为（0，n），
∵A点的坐标为（﹣4，0），∠ACD=90°，
∴AB2=AC2+BC2，
∵AC2=AO2+OC2，BC2=0B2+0C2，
∴AB2=AO2+OC2+0B2+0C2，
即（﹣n+4）2=42+n2+（﹣n）2+n2
解得n=﹣，n=0（舍去）．
故答案为：．
【点评】本题主要考查了一次函数图象上点的坐标特征及解直角三角形，解题的关键是利用勾股定理列出方程求n．
三 、解答题
【考点】一元二次方程的应用
【分析】考查了一元二次方程的应用，应熟记长方形的面积公式．另外求出4块种植地平移为一个长方形的长和宽是解决本题的关键
解：设小路的宽为xm，依题意有
（40-x）（32-x）=1140，
整理，得x2-72x+140=0．
解得x1=2，x2=70（不合题意，舍去）．
答：小路的宽应是2m
（1）t=1；（2）经过2或1.5s后，S△PCQ的面积为15cm2；（3）当点P运动1.75秒时，四边形BPQA的面积最小为： cm2．
【解析】(1)根据勾股定理PC2+CQ2=PQ2,便可求出经过1s后,P、Q两点的距离为 cm2;
(2)根据三角形的面积公式便可求出经过2或1.5s后,S△PCQ的面积为15 cm2;
(3)根据三角形的面积公式以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
解：（1）∵在Rt△ABC中，AC=24cm，BC=7cm，
∴AB=25cm，
设经过ts后，P、Q两点的距离为5cm，
ts后，PC=7-2t cm，CQ=5t cm，
根据勾股定理可知PC2+CQ2=PQ2，
代入数据（7-2t）2+（5t）2=（5）2；
解得t=1或t=-（不合题意舍去）；
（2）设经过ts后，S△PCQ的面积为15cm2
ts后，PC=7-2t cm，CQ=5t cm，
S△PCQ==×（7-2t）×5t=15
解得t1=2，t2=1.5，
经过2或1.5s后，S△PCQ的面积为15cm2
（3）设经过ts后，△PCQ的面积最大，则此时四边形BPQA的面积最小，
ts后，PC=7-2t cm，CQ=5t cm，
S△PCQ=×PC×CQ=×（7-2t）×5t=×（-2t2+7t）
当t=-时，即t==1.75s时，△PCQ的面积最大，
即S△PCQ=×PC×CQ=×（7-2×1.75）×5×1.752=（cm2），
∴四边形BPQA的面积最小值为：S△ABC-S△PCQ最大=×7×24-=（cm2），
当点P运动1.75秒时，四边形BPQA的面积最小为： cm2．
经过2s或4s△PCQ的面积是2cm2
【解析】试题分析：设经过xs△PCQ的面积是2cm2，由题意可得QC=xcm，PC=（6-x）cm，根据锐角三角函数再求得PC边上的高为xcm，根据三角形的面积公式列出方程（6﹣x）×x=2，解方程即可.
试题解析：
设经过xs△PCQ的面积是2cm2，由题意得
（6﹣x）×x=2
解得：x1=2，x2=4，
答：经过2s或4s△PCQ的面积是2cm2．
【考点】一元二次方程的应用．
【分析】（1）根据题意表示出长方形的长，进而利用长×宽=面积，求出即可；
（2）分别计算出每一规格的地板砖所需的费用，然后比较即可．
（1）设这地面矩形的长是xm，则依题意得：
x（20﹣x）=96，
解得x1=12，x2=8（舍去），
答：这地面矩形的长是12米；
（2）规格为0.80×0.80所需的费用：96×（0.80×0.80）×55=8250（元）．
规格为1.00×1.00所需的费用：96×（1.00×1.00）×80=7680（元）．
因为8250＜7680，
所以采用规格为1.00×1.00所需的费用较少．
（1）2秒或4秒；（2）线段PQ不能否将△ABC分成面积相等的两部分.
【解析】试题分析：（1）设出运动所求的时间，可将BP和BQ的长表示出来，代入三角形面积公式，列出等式，可将时间求出；
（2）将△PBQ的面积表示出来，根据△=b2-4ac来判断．
试题解析：（1）设经过x秒，使△PBQ的面积等于8cm2，依题意有：
（6-x） 2x=8，
解得x1=2，x2=4，
经检验，x1，x2均符合题意，
故经过2秒或4秒，△PBQ的面积等于8cm2；
（2）不能，理由如下：
设经过y秒，线段PQ能将△ABC分成面积相等的两部分，依题意有：
S△ABC =×6×8=24，
（6﹣y） 2y=12，
y2﹣6y+12=0，
∵△=b2﹣4ac=36﹣4×12=﹣12＜0，
∴此方程无实数根，
∴线段PQ不能否将△ABC分成面积相等的两部分.
【考点】一次函数综合题
【分析】（1）通过解方程x2﹣14x+48=0可以求得OC=6，OA=8．则C（0，6）；
（2）设直线MN的解析式是y=kx+b（k≠0）．把点A、C的坐标分别代入解析式，列出关于系数k、b的方程组，通过解方程组即可求得它们的值；
（3）需要分类讨论：PB为腰，PB为底两种情况下的点P的坐标．根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答
解答：解：（1）解方程x2﹣14x+48=0得
x1=6，x2=8．
∵OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根，
∴OC=6，OA=8．
∴C（0，6）；
（2）设直线MN的解析式是y=kx+b（k≠0）．
由（1）知，OA=8，则A（8，0）．
∵点A、C都在直线MN上，
∴，
解得，，
∴直线MN的解析式为y=﹣x+6；
（3）∵A（8，0），C（0，6），
∴根据题意知B（8，6）．
∵点P在直线MNy=﹣x+6上，
∴设P（a，﹣a+6）
当以点P，B，C三点为顶点的三角形是等腰三角形时，需要分类讨论：
①当PC=PB时，点P是线段BC的中垂线与直线MN的交点，则P1（4，3）；
②当PC=BC时，a2+（﹣a+6﹣6）2=64，
解得，a=，则P2（﹣，），P3（，）；
③当PB=BC时，（a﹣8）2+（﹣a+6﹣6）2=64，
解得，a=，则﹣a+6=﹣，∴P4（，﹣）．
综上所述，符合条件的点P有：P1（4，3），P2（﹣，）P3（，），P4（，﹣）．
【考点】正方形的性质；全等三角形的判定与性质；勾股定理．
【分析】（1）由三角形全等可以证明AH=AB，
（2）延长CB至E，使BE=DN，证明△AEM≌△ANM，能得到AH=AB，
（3）分别沿AM、AN翻折△AMH和△ANH，得到△ABM和△AND，然后分别延长BM和DN交于点C，得正方形ABCE，设AH=x，则MC=x﹣2，NC=x﹣3，在Rt△MCN中，由勾股定理，解得x．
解：（1）如图①AH=AB．
（2）数量关系成立．如图②，延长CB至E，使BE=DN．
∵ABCD是正方形，
∴AB=AD，∠D=∠ABE=90°，
在Rt△AEB和Rt△AND中，，
∴Rt△AEB≌Rt△AND，
∴AE=AN，∠EAB=∠NAD，
∴∠EAM=∠NAM=45°，
在△AEM和△ANM中，，
∴△AEM≌△ANM．
∴S△AEM=S△ANM，EM=MN，
∵AB、AH是△AEM和△ANM对应边上的高，
∴AB=AH．
（3）如图③分别沿AM、AN翻折△AMH和△ANH，得到△ABM和△AND，
∴BM=2，DN=3，∠B=∠D=∠BAD=90°．
分别延长BM和DN交于点C，得正方形ABCD，
由（2）可知，AH=AB=BC=CD=AD．
设AH=x，则MC=x﹣2，NC=x﹣3，
在Rt△MCN中，由勾股定理，得MN2=MC2+NC2
∴52=（x﹣2）2+（x﹣3）2
解得x1=6，x2=﹣1．（不符合题意，舍去）
∴AH=6．
【点评】本题主要考查正方形的性质和三角形全等的判断，难度中等．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)