安徽省滁州市第三中学高中数学人教A版必修1课件: 第一章1.3.2 函数的奇偶性
文档属性
| 名称 | 安徽省滁州市第三中学高中数学人教A版必修1课件: 第一章1.3.2 函数的奇偶性 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-07 11:24:49 | ||
图片预览





文档简介
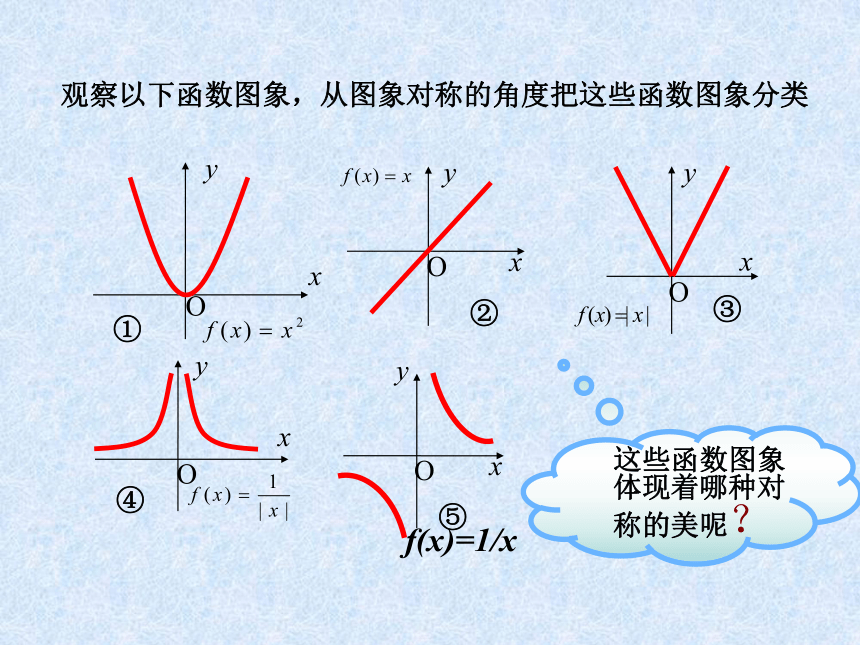
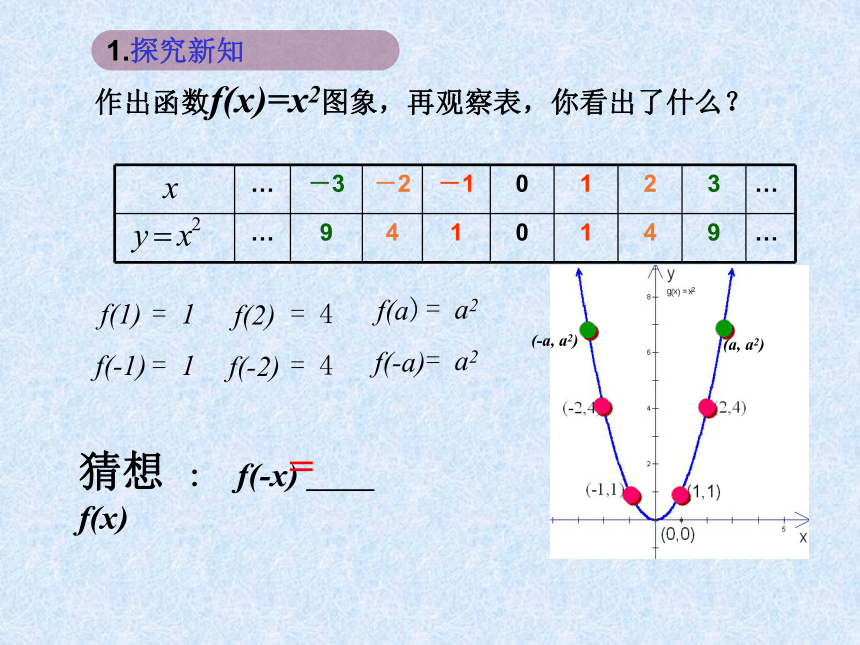
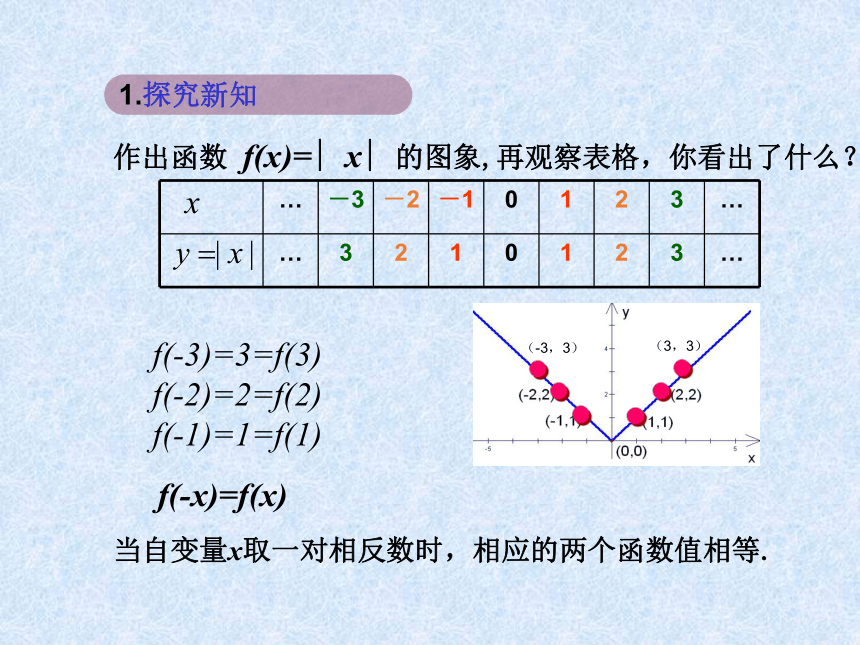
课件20张PPT。 同学们,大家上午好!从这些图片中你感受到了什么?这些几何图形中又体现了什么?观察以下函数图象,从图象对称的角度把这些函数图象分类这些函数图象体现着哪种对称的美呢?f(x)=1/x1.3.2 奇偶性作出函数f(x)=x2图象,再观察表,你看出了什么?猜想 : f(-x) ____ f(x)=1.探究新知当自变量x取一对相反数时,相应的两个函数值相等.f(-3)=3=f(3) f(-2)=2=f(2) f(-1)=1=f(1)作出函数 f(x)=∣x∣的图象,再观察表格,你看出了什么?1.探究新知f(-x)=f(x) 结论:当自变量x在定义域内任取一对相反数时,相应的两个函数值相同;
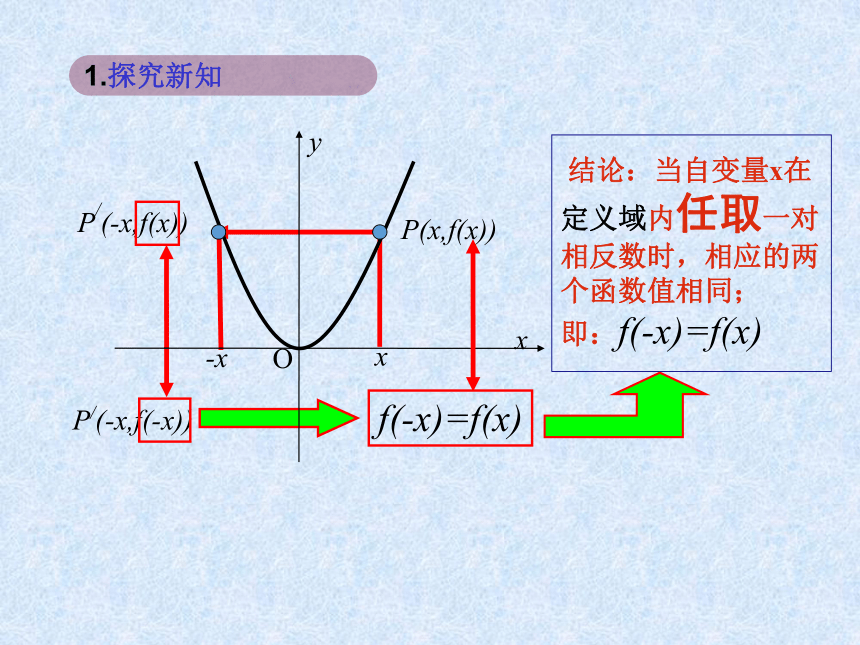
即:f(-x)=f(x)x P(x,f(x))P/(-x,f(x))-xP/(-x,f(-x))f(-x)=f(x)1.探究新知 图象关于原点中心对称的函数与函数式有怎样的关系?偶函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数.1.探究新知f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)f(-x)=-x=-f(x)f(-x)=-1/x=-f(x)1.探究新知奇函数:一般地,如果函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数.1.探究新知☆对奇函数、偶函数定义的说明:(1)如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具备奇偶性.函数的奇偶性是函数的整体性质.
(2)函数具有奇偶性:对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量.定义域关于原点对称2.勤于总结(3)思考:已知函数 f(x)=x3+x 为奇函数,它的一
部分图象如下图所示,你可以用你刚刚学的知识画出
它的另外一部分图象吗?例5. 判断下列函数的奇偶性:(1) f(x)=x4 (2) f(x)=x+1/x(3) f(x)=x5 (4) f(x)=1/ x23.例题讲解总结:判断函数奇偶性步骤
(1)首先确定函数的定义域,并判断其定义域是否关于原点对称;
(2)确定f(-x)与f(x)的关系
(3)作出相应结论:
若f(-x) = f(x)或f(-x) -f(x) = 0,则f(x)是偶函数;
若f(-x) =-f(x)或 f(-x)+f(x) = 0,则f(x)是奇函数.变式训练: 判断下列函数的奇偶性:
(1)f(x)=x3 (2)f(x)=x4 +1
奇函数 偶函数
(3)f(x)=x4 +1,x∈(-2,2]
非奇非偶函数
(4)f(x)=0
既奇且偶函数
4.巩固新知既不是奇函数也不是偶函数的函数称为非奇非偶函数;
既是奇函数又是偶函数的函数称为既奇且偶函数.偶函数非奇非偶函数奇函数例6.判断下列函数的奇偶性:非奇非偶函数5.想一想(4)yo6.课时小结,知识建构 判断函数奇偶性的基本步骤:注意:若可以作出函数图象的,直接观察图象是否关于y轴对称或者关于原点对称。6.课时小结,知识建构7.布置作业P36 1、2同学们,再见!
即:f(-x)=f(x)x P(x,f(x))P/(-x,f(x))-xP/(-x,f(-x))f(-x)=f(x)1.探究新知 图象关于原点中心对称的函数与函数式有怎样的关系?偶函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数.1.探究新知f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)f(-x)=-x=-f(x)f(-x)=-1/x=-f(x)1.探究新知奇函数:一般地,如果函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数.1.探究新知☆对奇函数、偶函数定义的说明:(1)如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具备奇偶性.函数的奇偶性是函数的整体性质.
(2)函数具有奇偶性:对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量.定义域关于原点对称2.勤于总结(3)思考:已知函数 f(x)=x3+x 为奇函数,它的一
部分图象如下图所示,你可以用你刚刚学的知识画出
它的另外一部分图象吗?例5. 判断下列函数的奇偶性:(1) f(x)=x4 (2) f(x)=x+1/x(3) f(x)=x5 (4) f(x)=1/ x23.例题讲解总结:判断函数奇偶性步骤
(1)首先确定函数的定义域,并判断其定义域是否关于原点对称;
(2)确定f(-x)与f(x)的关系
(3)作出相应结论:
若f(-x) = f(x)或f(-x) -f(x) = 0,则f(x)是偶函数;
若f(-x) =-f(x)或 f(-x)+f(x) = 0,则f(x)是奇函数.变式训练: 判断下列函数的奇偶性:
(1)f(x)=x3 (2)f(x)=x4 +1
奇函数 偶函数
(3)f(x)=x4 +1,x∈(-2,2]
非奇非偶函数
(4)f(x)=0
既奇且偶函数
4.巩固新知既不是奇函数也不是偶函数的函数称为非奇非偶函数;
既是奇函数又是偶函数的函数称为既奇且偶函数.偶函数非奇非偶函数奇函数例6.判断下列函数的奇偶性:非奇非偶函数5.想一想(4)yo6.课时小结,知识建构 判断函数奇偶性的基本步骤:注意:若可以作出函数图象的,直接观察图象是否关于y轴对称或者关于原点对称。6.课时小结,知识建构7.布置作业P36 1、2同学们,再见!
