高中数学人教A版必修1课件: 第一章1.3.2 函数的奇偶性
文档属性
| 名称 | 高中数学人教A版必修1课件: 第一章1.3.2 函数的奇偶性 |

|
|
| 格式 | zip | ||
| 文件大小 | 231.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-07 00:00:00 | ||
图片预览




文档简介
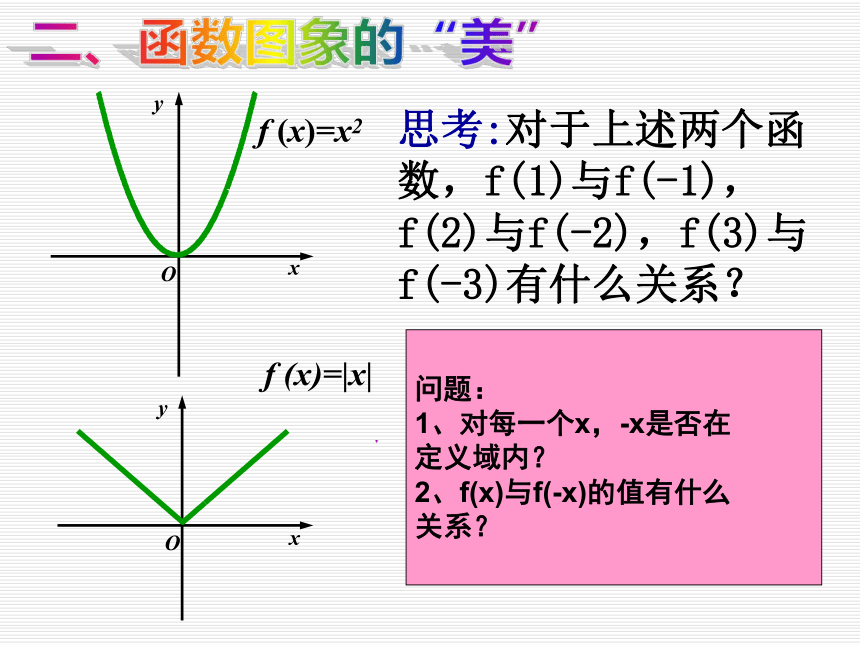
课件15张PPT。函数的奇偶性一、现实生活中的“美”的事例二、函数图象的“美” f (x)=x2 f (x)=|x|问题:
1、对每一个x,-x是否在
定义域内?
2、f(x)与f(-x)的值有什么
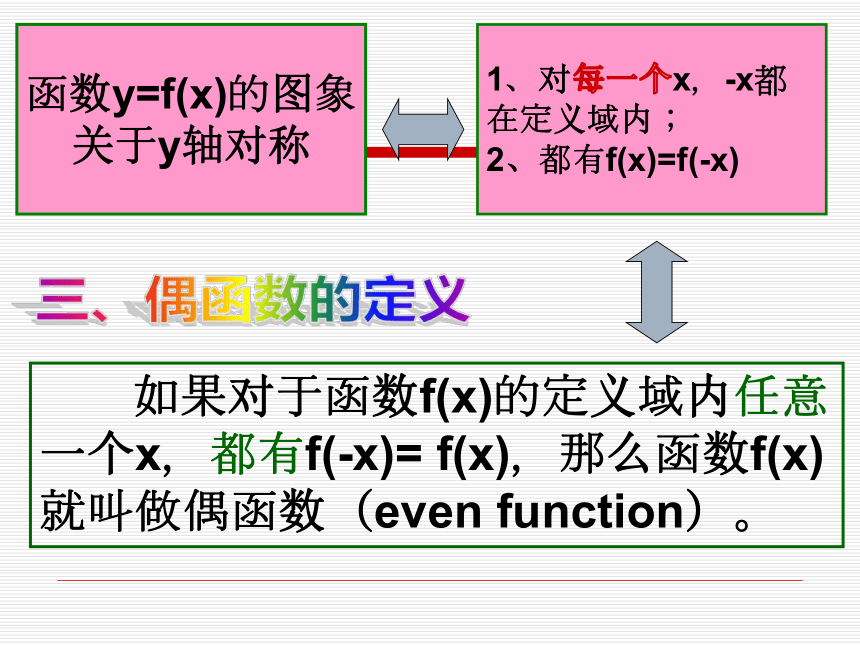
关系?思考:对于上述两个函数,f(1)与f(-1),f(2)与f(-2),f(3)与f(-3)有什么关系? 函数y=f(x)的图象
关于y轴对称1、对每一个x,-x都
在定义域内;
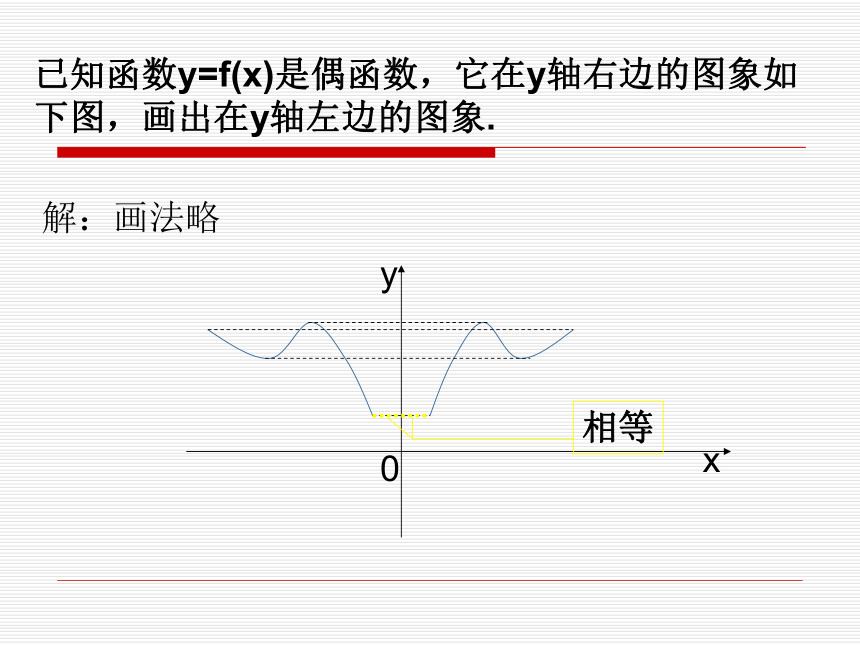
2、都有f(x)=f(-x)三、偶函数的定义 如果对于函数f(x)的定义域内任意一个x,都有f(-x)= f(x),那么函数f(x)就叫做偶函数(even fun_ction)。 已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.解:画法略四、偶函数的判定(x,f(x))(-x,-f(x))因为点M`在函数图象上,
所以其坐标又为(-x,f(-x))函数y=f(x)的图象
关于原点对称1、对定义域中的每一
个x,-x是也在定义
域内;
2、都有f(-x)=-f(x)五、奇函数的定义 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=- f(x),那么函数f(x)就叫做奇函数(odd fun_ction) 。 已知函数y=f(x)是奇函数,它在y轴右边的图象如下图,画出在y轴左边的图象. 判定函数奇偶性基本方法:
①定义法:
先看定义域是否关于原点对称,再看f(-x)与f(x)的关系.
②图象法:
看图象是否关于原点或y轴对称.例1 判断下列函数的奇偶性:理论迁移自我思考:-15本课小结作业:P36 练习 1 (3)(4)
P39 练习A 6
1、对每一个x,-x是否在
定义域内?
2、f(x)与f(-x)的值有什么
关系?思考:对于上述两个函数,f(1)与f(-1),f(2)与f(-2),f(3)与f(-3)有什么关系? 函数y=f(x)的图象
关于y轴对称1、对每一个x,-x都
在定义域内;
2、都有f(x)=f(-x)三、偶函数的定义 如果对于函数f(x)的定义域内任意一个x,都有f(-x)= f(x),那么函数f(x)就叫做偶函数(even fun_ction)。 已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.解:画法略四、偶函数的判定(x,f(x))(-x,-f(x))因为点M`在函数图象上,
所以其坐标又为(-x,f(-x))函数y=f(x)的图象
关于原点对称1、对定义域中的每一
个x,-x是也在定义
域内;
2、都有f(-x)=-f(x)五、奇函数的定义 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=- f(x),那么函数f(x)就叫做奇函数(odd fun_ction) 。 已知函数y=f(x)是奇函数,它在y轴右边的图象如下图,画出在y轴左边的图象. 判定函数奇偶性基本方法:
①定义法:
先看定义域是否关于原点对称,再看f(-x)与f(x)的关系.
②图象法:
看图象是否关于原点或y轴对称.例1 判断下列函数的奇偶性:理论迁移自我思考:-15本课小结作业:P36 练习 1 (3)(4)
P39 练习A 6
