1.3.2 函数的奇偶性
图片预览





文档简介
课件17张PPT。高一数学必修1人教A版
1.3.2函数的奇偶性1
印度泰姬陵 函数图象的上升与下降反映了函数的单调性,而函数图象的最高点与最低点引发了函数的最值,那么从函数图象的对称性出发我们又能得到函数的什么性质?1.3.2函数的奇偶性1
1.了解函数奇偶性的含义;
2.掌握判断函数奇偶性的方法,能证明一些简单函数的奇偶性;
3.初步学会运用函数图象理解和研究函数的性质
4.知识网络
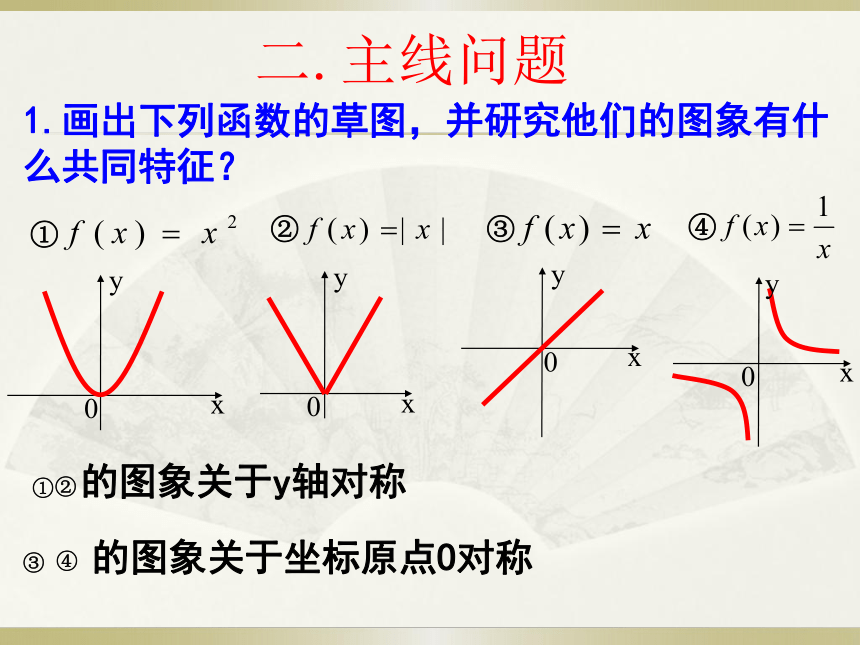
一.学习目标1.画出下列函数的草图,并研究他们的图象有什么共同特征?二.主线问题一般地,若函数y=f(x)的图象关于y轴对称,对于定义域内互为相反数的任意两个数x和-x都有f(-x)=f(x),我们把具有这种特征的函数叫做偶函数。 f(-x)=f(x)f(-x)=-f(x)(1)等式f(-x)=f(x)用文字语言表述
即自变量相反时对应的函数值相等。 5.函数图像与奇偶性:
奇函数的图像关于 对称;反之若一个函数的图像关
于原点对称,则该函数为 函数.
偶函数的图像关于 对称;反之若一个函数的图像关
于 对称,则该函数为偶函数.原点奇注意: (3)如果一个函数f(x)是奇函数或偶函数,那么我们就说
函数f(x)具有 ,奇偶性函数的奇偶性是函数的整体性质. (2)由奇偶函数的定义知,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量即定义域关于原点对称 等式f(-x)=-f(x)用文字语言表述
即自变量相反时对应的函数值也相反。 例1:根据下列函数图象,判断函数奇偶性.偶函数非奇非偶函数奇函数非奇非偶函数判断函数奇偶性的方法1:图象法三.例题预热例2:判断下列函数的奇偶性:定义域是否关于原点对称前提条件判断函数奇偶性的方法2:定义法
步骤:一看 定义域
二找 f(-x)= -f(x)或
f(-x)=f(x)的关系
三判断 奇或偶
判断下列函数的奇偶性四.跟踪训练五.分层练习3.如果定义在区间[3-a,5]上的函数f(x)是偶函数,则a=_______.2.已知函数 是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象。如果函数 是奇函数,图象又如何?归纳总结x3.奇偶性是函数的整体性质。 4.判断函数奇偶性的方法: (1)图像法 (2)定义法 谢谢大家,再见!
印度泰姬陵 函数图象的上升与下降反映了函数的单调性,而函数图象的最高点与最低点引发了函数的最值,那么从函数图象的对称性出发我们又能得到函数的什么性质?1.3.2函数的奇偶性1
1.了解函数奇偶性的含义;
2.掌握判断函数奇偶性的方法,能证明一些简单函数的奇偶性;
3.初步学会运用函数图象理解和研究函数的性质
4.知识网络
一.学习目标1.画出下列函数的草图,并研究他们的图象有什么共同特征?二.主线问题一般地,若函数y=f(x)的图象关于y轴对称,对于定义域内互为相反数的任意两个数x和-x都有f(-x)=f(x),我们把具有这种特征的函数叫做偶函数。 f(-x)=f(x)f(-x)=-f(x)(1)等式f(-x)=f(x)用文字语言表述
即自变量相反时对应的函数值相等。 5.函数图像与奇偶性:
奇函数的图像关于 对称;反之若一个函数的图像关
于原点对称,则该函数为 函数.
偶函数的图像关于 对称;反之若一个函数的图像关
于 对称,则该函数为偶函数.原点奇注意: (3)如果一个函数f(x)是奇函数或偶函数,那么我们就说
函数f(x)具有 ,奇偶性函数的奇偶性是函数的整体性质. (2)由奇偶函数的定义知,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量即定义域关于原点对称 等式f(-x)=-f(x)用文字语言表述
即自变量相反时对应的函数值也相反。 例1:根据下列函数图象,判断函数奇偶性.偶函数非奇非偶函数奇函数非奇非偶函数判断函数奇偶性的方法1:图象法三.例题预热例2:判断下列函数的奇偶性:定义域是否关于原点对称前提条件判断函数奇偶性的方法2:定义法
步骤:一看 定义域
二找 f(-x)= -f(x)或
f(-x)=f(x)的关系
三判断 奇或偶
判断下列函数的奇偶性四.跟踪训练五.分层练习3.如果定义在区间[3-a,5]上的函数f(x)是偶函数,则a=_______.2.已知函数 是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象。如果函数 是奇函数,图象又如何?归纳总结x3.奇偶性是函数的整体性质。 4.判断函数奇偶性的方法: (1)图像法 (2)定义法 谢谢大家,再见!
