函数的奇偶性
图片预览




文档简介
课件16张PPT。函数的奇偶性
学习目标1、理解函数奇偶性的概念及其图像特征:
2、会判断函数的奇偶性:
3、会用定义证明函数的奇偶性:
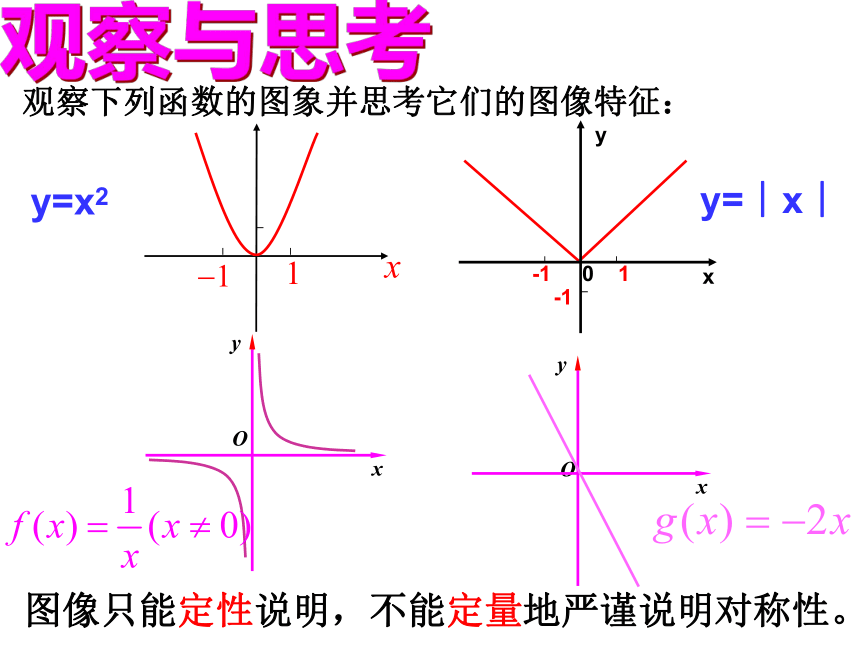
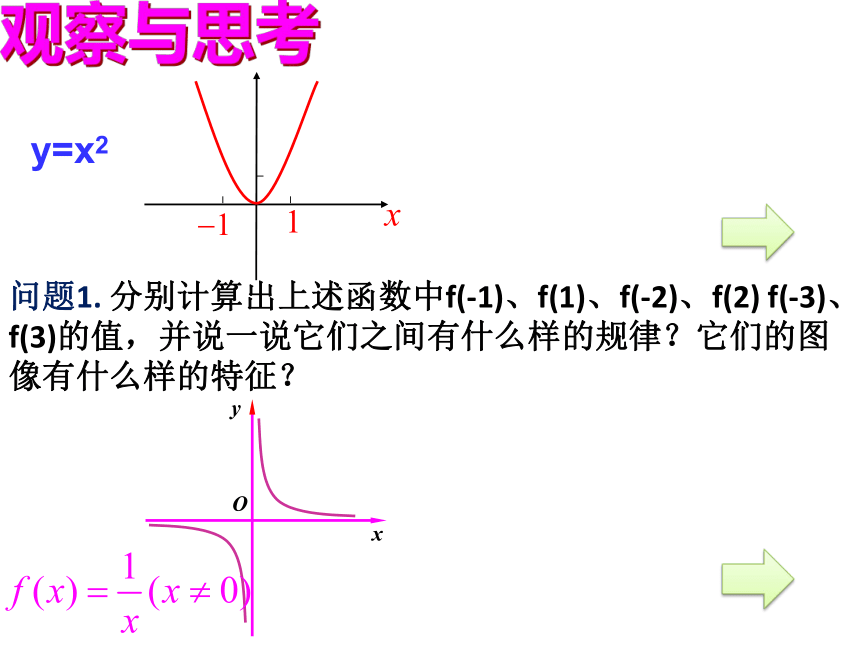
4、会简单地运用奇偶性的定义:y=x2y=︱x︱观察与思考观察下列函数的图象并思考它们的图像特征:图像只能定性说明,不能定量地严谨说明对称性。y=x2观察与思考问题1. 分别计算出上述函数中f(-1)、f(1)、f(-2)、f(2) f(-3)、f(3)的值,并说一说它们之间有什么样的规律?它们的图像有什么样的特征?
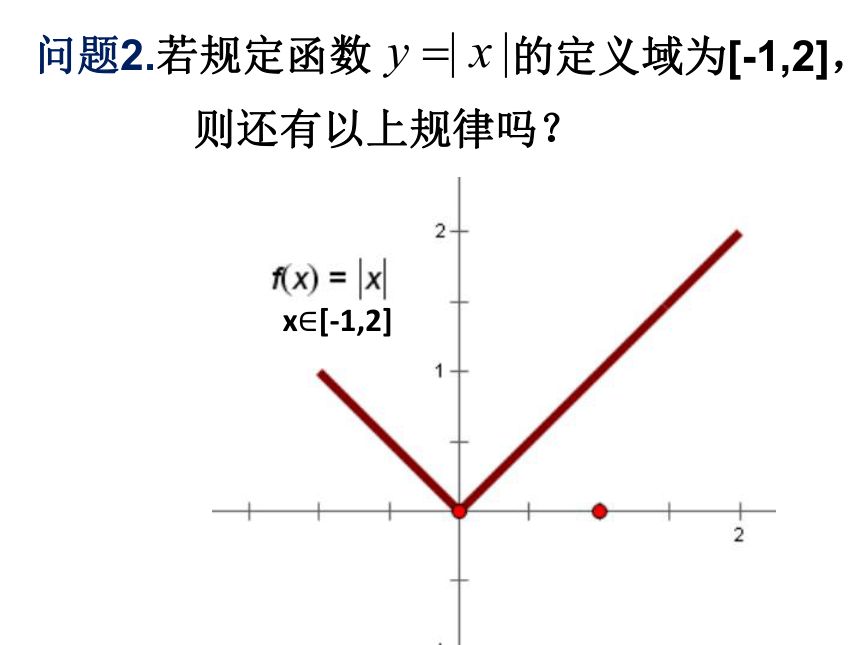
问题2.若规定函数的定义域为[-1,2],则还有以上规律吗?? 一般地,对于定义域内任意一个数 ,都有
那么称函数 是偶函数(even fun_ction).1.偶函数的定义函数图象关于y轴对称你能举出一些偶函数的例子?概念学习 一般地,对于定义域内任意一个数 ,都有
那么称函数 是奇函数(odd fun_ction).概念学习1.奇函数的定义函数图象关于原点对称你能举出一些奇函数的例子?问题3.若奇函数在x=0处有意义,则f(0)=1吗?若偶函数在x=0处有意义,则f(0)呢?例1.根据下列函数图象,判断函数奇偶性.
yxyxyx-12yx-11偶奇非奇
非偶奇例2、判断下列函数的奇偶性:(2)解:定义域为R ∵ f(-x)=(-x)4=f(x)即f(-x)=f(x)∴f(x)为偶函数(3)解:定义域为R ∵ f(-x)=(-x)5=-x=-f(x)即f(-x)=-f(x)∴f(x)为奇函数定义域优先(5)解:定义域为R
∵ f(-x)=-0=-f(x)
∵ f(-x)=-0=0=f(x) 即f(-x)=-f(x)∴f(x)为既奇又偶函数例2、判断下列函数的奇偶性:定义域优先即f(-x)=f(x)小结:根据奇偶性,函数可划分为四类:
①偶函数 ; ②奇函数;
③既奇又偶函数 ; ④非奇非偶函数。(1)、先求定义域,看是否关于原点对称; (2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.问题5:针对以上所学的奇偶函数,你能发现奇偶函数解析式有何特征吗?问题4:你能总结用定义法判断函数的奇偶性的一般步骤吗? 定义转化,引伸提高定义转化,引伸提高变式3:求f(x)的解析式课堂小结
(1)一个概念,一种思想方法:
奇偶性 数形结合
(2)两种方法:
图像法、定义法
学习目标1、理解函数奇偶性的概念及其图像特征:
2、会判断函数的奇偶性:
3、会用定义证明函数的奇偶性:
4、会简单地运用奇偶性的定义:
学习目标1、理解函数奇偶性的概念及其图像特征:
2、会判断函数的奇偶性:
3、会用定义证明函数的奇偶性:
4、会简单地运用奇偶性的定义:y=x2y=︱x︱观察与思考观察下列函数的图象并思考它们的图像特征:图像只能定性说明,不能定量地严谨说明对称性。y=x2观察与思考问题1. 分别计算出上述函数中f(-1)、f(1)、f(-2)、f(2) f(-3)、f(3)的值,并说一说它们之间有什么样的规律?它们的图像有什么样的特征?
问题2.若规定函数的定义域为[-1,2],则还有以上规律吗?? 一般地,对于定义域内任意一个数 ,都有
那么称函数 是偶函数(even fun_ction).1.偶函数的定义函数图象关于y轴对称你能举出一些偶函数的例子?概念学习 一般地,对于定义域内任意一个数 ,都有
那么称函数 是奇函数(odd fun_ction).概念学习1.奇函数的定义函数图象关于原点对称你能举出一些奇函数的例子?问题3.若奇函数在x=0处有意义,则f(0)=1吗?若偶函数在x=0处有意义,则f(0)呢?例1.根据下列函数图象,判断函数奇偶性.
yxyxyx-12yx-11偶奇非奇
非偶奇例2、判断下列函数的奇偶性:(2)解:定义域为R ∵ f(-x)=(-x)4=f(x)即f(-x)=f(x)∴f(x)为偶函数(3)解:定义域为R ∵ f(-x)=(-x)5=-x=-f(x)即f(-x)=-f(x)∴f(x)为奇函数定义域优先(5)解:定义域为R
∵ f(-x)=-0=-f(x)
∵ f(-x)=-0=0=f(x) 即f(-x)=-f(x)∴f(x)为既奇又偶函数例2、判断下列函数的奇偶性:定义域优先即f(-x)=f(x)小结:根据奇偶性,函数可划分为四类:
①偶函数 ; ②奇函数;
③既奇又偶函数 ; ④非奇非偶函数。(1)、先求定义域,看是否关于原点对称; (2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.问题5:针对以上所学的奇偶函数,你能发现奇偶函数解析式有何特征吗?问题4:你能总结用定义法判断函数的奇偶性的一般步骤吗? 定义转化,引伸提高定义转化,引伸提高变式3:求f(x)的解析式课堂小结
(1)一个概念,一种思想方法:
奇偶性 数形结合
(2)两种方法:
图像法、定义法
学习目标1、理解函数奇偶性的概念及其图像特征:
2、会判断函数的奇偶性:
3、会用定义证明函数的奇偶性:
4、会简单地运用奇偶性的定义:
