1.3.1单调性与最大(小)值
文档属性
| 名称 | 1.3.1单调性与最大(小)值 |  | |
| 格式 | zip | ||
| 文件大小 | 375.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-07 12:29:02 | ||
图片预览


文档简介
课件22张PPT。函数的单调性
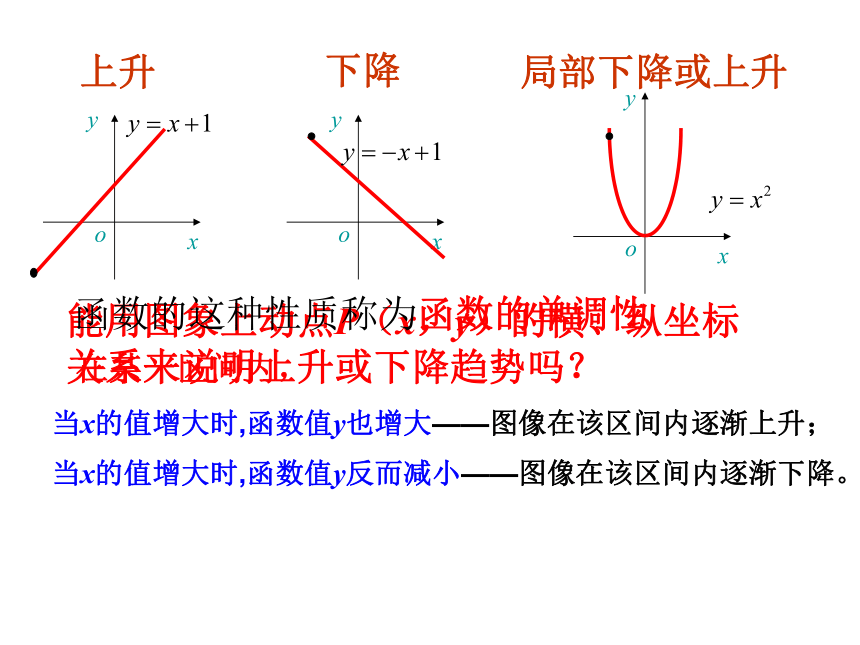
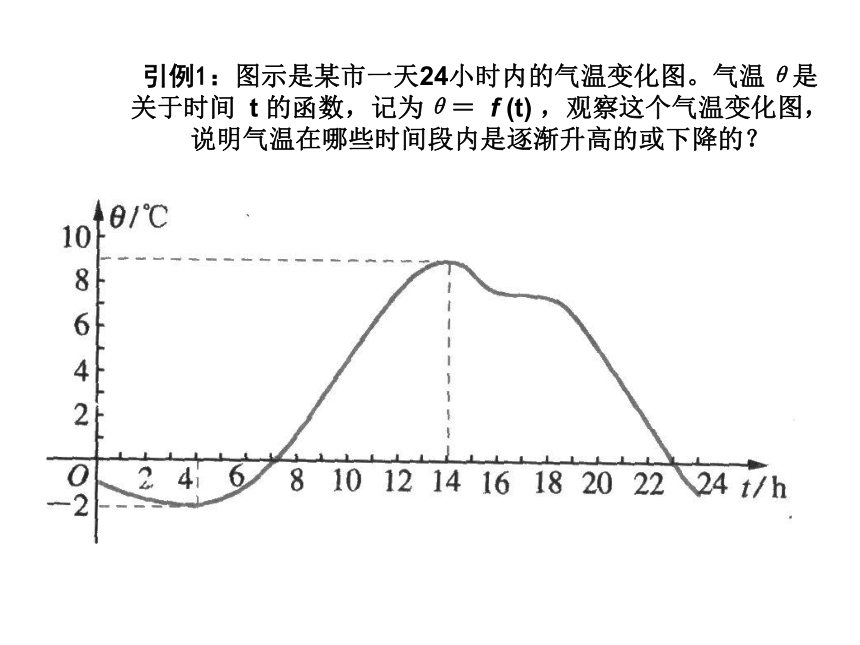
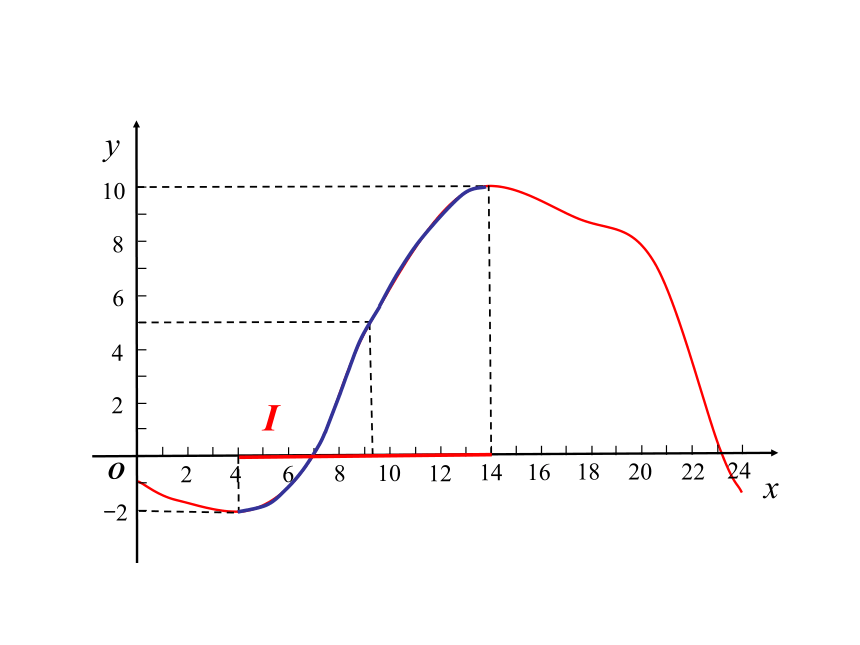
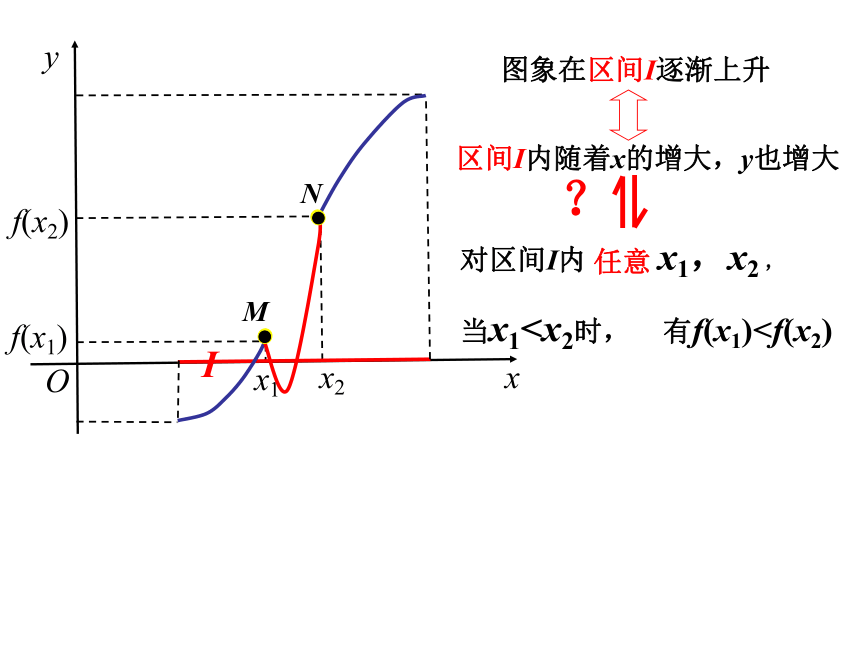
能用图象上动点P(x,y)的横、纵坐标关系来说明上升或下降趋势吗?函数的这种性质称为函数的单调性局部下降或上升下降上升引例1:图示是某市一天24小时内的气温变化图。气温θ是关于时间 t 的函数,记为θ= f (t) ,观察这个气温变化图,说明气温在哪些时间段内是逐渐升高的或下降的? 对区间I内 x1,x2 ,
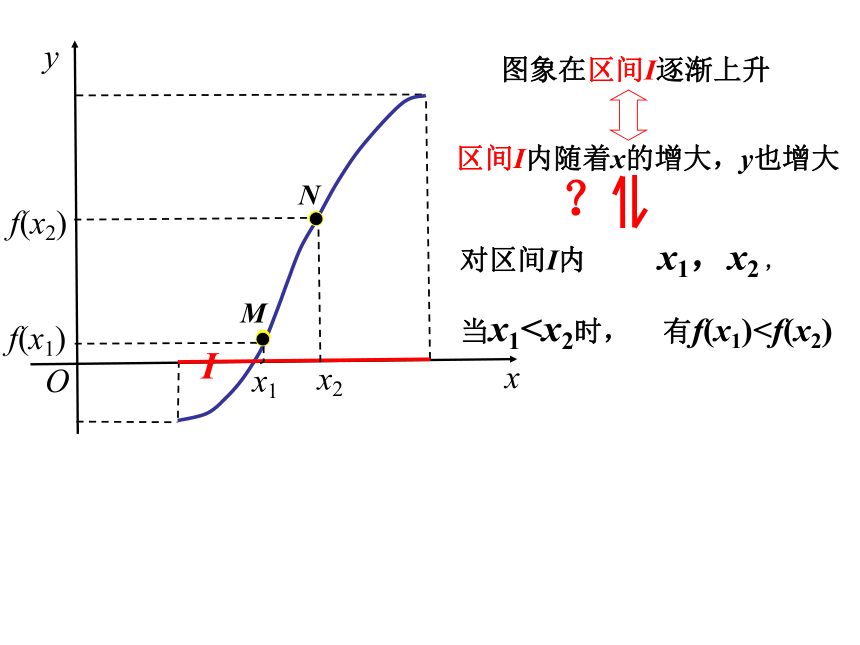
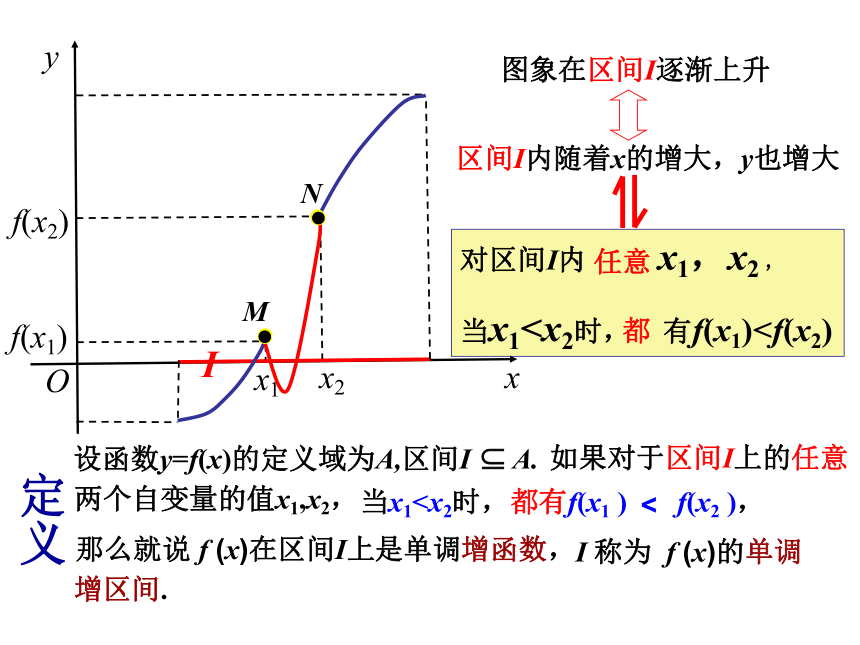
当x1当x1当x1MN任意两个自变量的值x1,x2,区间I内随着x的增大,y也增大图象在区间I逐渐上升I 那么就说在f(x)这个区间上是单调
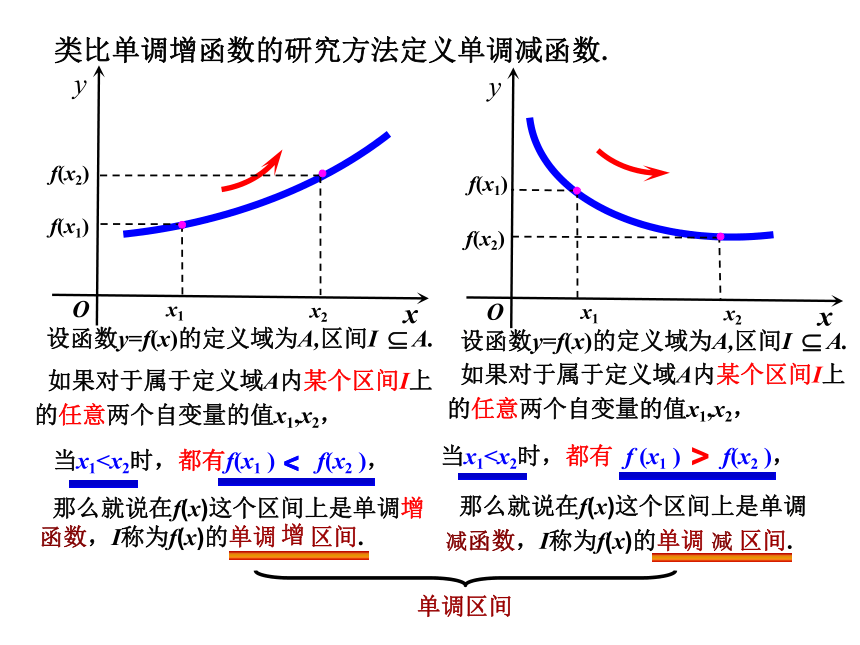
减函数,I称为f(x)的单调 减 区间.类比单调增函数的研究方法定义单调减函数.x 如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2, 如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2, 那么就说在f(x)这个区间上是单调增 函数,I称为f(x)的单调 区间.增当x1单调区间(2)函数单调性是针对某个区间而言的,是一个局部性质;(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
在单调区间上,增函数的图象是上升的,减函数的图象是下降的。注意:(2)函数单调性是针对某个区间而言的,是一个局部性质;(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
在单调区间上,增函数的图象是上升的,减函数的图象是下降的。注意:判断2:定义在R上的函数 f (x)满足 f (2)> f(1),则函数 f (x)在R上是增函数;(3) x 1, x 2 取值的任意性 例1:如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上, y=f(x)是增函数还是减函数。 单调增区间是 [-2,1), [3, 5] 。答:函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),
[3,5] 其中 单调减区间是 [-5, -2), [1,3) , 注意!用逗号间隔开题型一:图像法求函数单调区间变式1:求y=x2-4x+5的单调区间.变式2: y=x2-ax+4在[2,4]上是
单调函数,求a的取值范围.变式3: 求函数 的单调区间注意:函数的单调性,即它是增函数还是减函数,都是针对该函数的定义域内的某个区间而言.因此在讲一个函数是增函数还是减函数,必须指明是在定义域的哪个区间上.题型二:定义法证明函数单调性例2:证明函数f(x)=3x+2在R上是增函数。取值作差定号下结论比较变形:因式分解或配方变形讨论变式1:函数f(x)=-3x+2在R上是增函数
还是减函数?变式2:函数f(x)=kx+b(k≠0)在R上是增
函数还是减函数?练习1:画出下列函数图像,并写出单调区间数缺形时少直观,练习2:判断函数 在定义域
上的单调性.
给出证明形少数时难入微所以函数 在区间上 是增函数. 取值作差变形定号结论 学而不思则罔,思而不学则殆
小结
1.函数单调性的定义中有哪些关键点?
2.有几种方法判断函数单调性?
3.你学会了什么数学思想方法?温故而知新,可以为师矣
作业2、判断函数 f(x)= 在 上的单调性。
3、判断函数 f(x)= 在(-1,1)上的
单 调性。
1、习题1.3A组第2题谢谢指导!练习实践BA
3下列函数中,在区间 内是减函数的是( )
A B C D
4函数 在区间 上是减函数 ,则( )
A B C D
5函数 在 是增函数,
在 上是减函数,则 ( )
A -3 B 13 C 7 D 由而定的常数
CDB6求证:函数 在区间 上是否具有单调性? (校本例1)
能用图象上动点P(x,y)的横、纵坐标关系来说明上升或下降趋势吗?函数的这种性质称为函数的单调性局部下降或上升下降上升引例1:图示是某市一天24小时内的气温变化图。气温θ是关于时间 t 的函数,记为θ= f (t) ,观察这个气温变化图,说明气温在哪些时间段内是逐渐升高的或下降的? 对区间I内 x1,x2 ,
当x1
减函数,I称为f(x)的单调 减 区间.类比单调增函数的研究方法定义单调减函数.x 如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2, 如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2, 那么就说在f(x)这个区间上是单调增 函数,I称为f(x)的单调 区间.增当x1
在单调区间上,增函数的图象是上升的,减函数的图象是下降的。注意:(2)函数单调性是针对某个区间而言的,是一个局部性质;(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
在单调区间上,增函数的图象是上升的,减函数的图象是下降的。注意:判断2:定义在R上的函数 f (x)满足 f (2)> f(1),则函数 f (x)在R上是增函数;(3) x 1, x 2 取值的任意性 例1:如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上, y=f(x)是增函数还是减函数。 单调增区间是 [-2,1), [3, 5] 。答:函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),
[3,5] 其中 单调减区间是 [-5, -2), [1,3) , 注意!用逗号间隔开题型一:图像法求函数单调区间变式1:求y=x2-4x+5的单调区间.变式2: y=x2-ax+4在[2,4]上是
单调函数,求a的取值范围.变式3: 求函数 的单调区间注意:函数的单调性,即它是增函数还是减函数,都是针对该函数的定义域内的某个区间而言.因此在讲一个函数是增函数还是减函数,必须指明是在定义域的哪个区间上.题型二:定义法证明函数单调性例2:证明函数f(x)=3x+2在R上是增函数。取值作差定号下结论比较变形:因式分解或配方变形讨论变式1:函数f(x)=-3x+2在R上是增函数
还是减函数?变式2:函数f(x)=kx+b(k≠0)在R上是增
函数还是减函数?练习1:画出下列函数图像,并写出单调区间数缺形时少直观,练习2:判断函数 在定义域
上的单调性.
给出证明形少数时难入微所以函数 在区间上 是增函数. 取值作差变形定号结论 学而不思则罔,思而不学则殆
小结
1.函数单调性的定义中有哪些关键点?
2.有几种方法判断函数单调性?
3.你学会了什么数学思想方法?温故而知新,可以为师矣
作业2、判断函数 f(x)= 在 上的单调性。
3、判断函数 f(x)= 在(-1,1)上的
单 调性。
1、习题1.3A组第2题谢谢指导!练习实践BA
3下列函数中,在区间 内是减函数的是( )
A B C D
4函数 在区间 上是减函数 ,则( )
A B C D
5函数 在 是增函数,
在 上是减函数,则 ( )
A -3 B 13 C 7 D 由而定的常数
CDB6求证:函数 在区间 上是否具有单调性? (校本例1)
