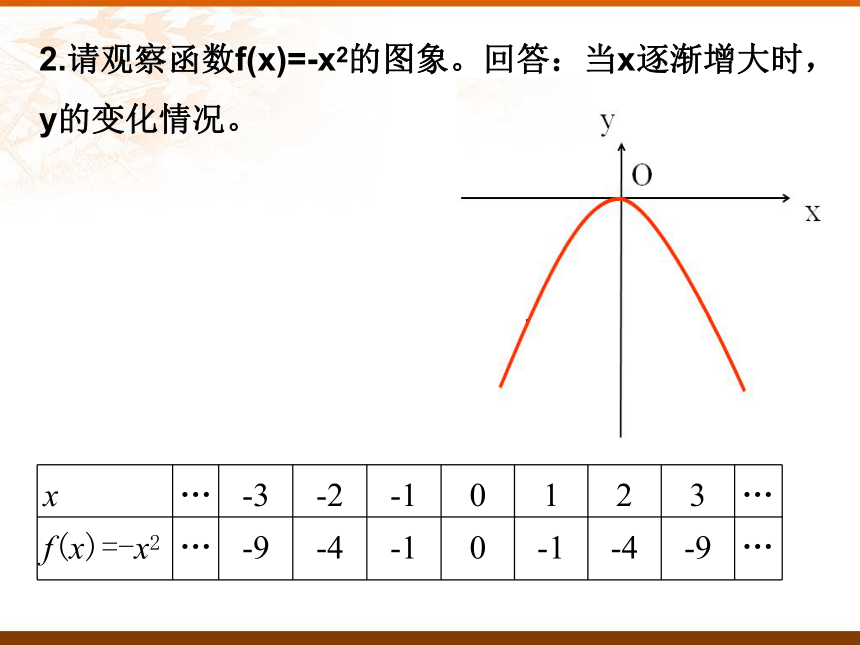
1.3.1 函数的单调性
图片预览




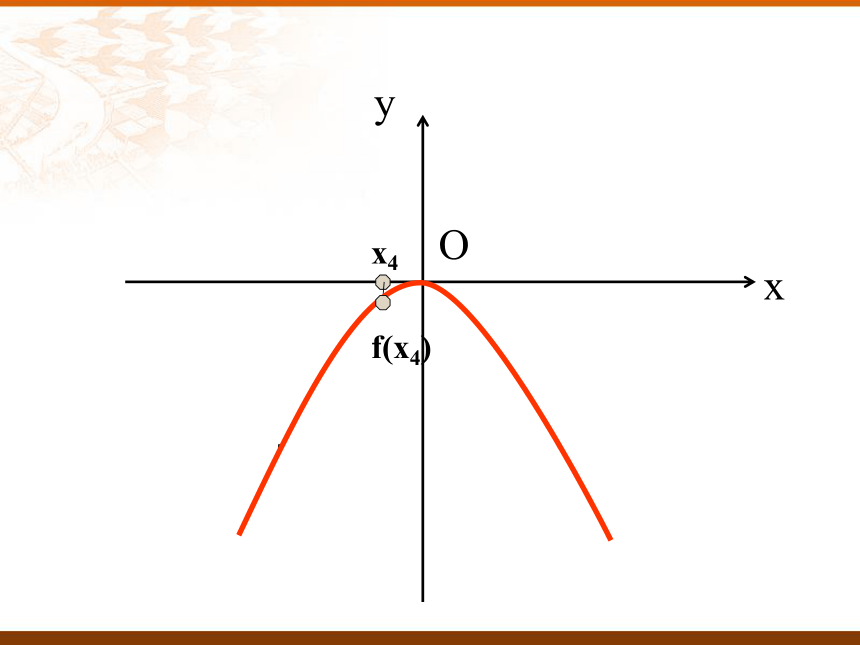
文档简介
课件23张PPT。1.3.1 函数的单调性科比投篮1.通过观看科比帅气的投篮,我们看到篮球从科比手上离开之后划过优美的曲线,落入篮筐。
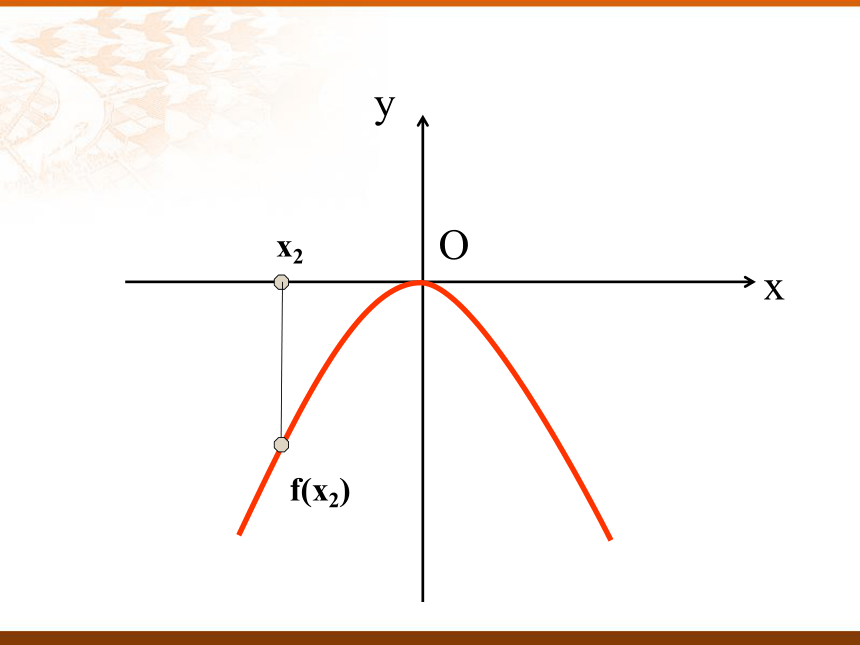
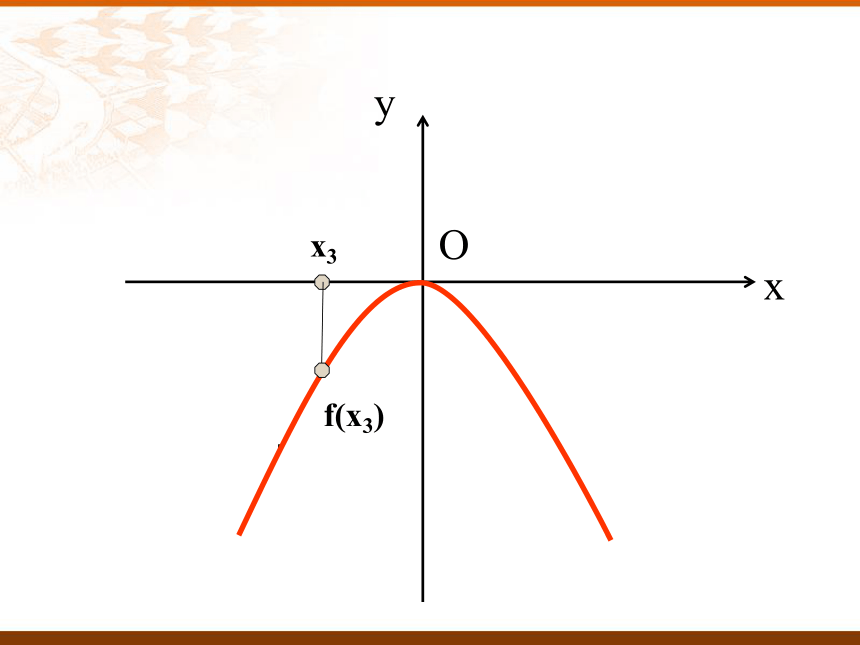
那请同学们回忆一下:刚刚视频中篮球投出之后篮球的高度是怎样变化的?教学过程:一、课题导入:我们可以看出:随着篮球的前进篮球高度开始是上升的,达到最高点后是逐渐下降的。2.请观察函数f(x)=-x2的图象。回答:当x逐渐增大时, y的变化情况。下面我们以动态的过程来研究函数f(x)=-x2函数值y随着x的增大的变化情况Oxyx1f(x1)Oxyx2f(x2)Oxyx3f(x3)Oxyx4f(x4)Oxyx5f(x5)Oxyx6f(x6)Oxyx7f(x7)Oxyx8f(x8)Oxyx9f(x9)函数f (x)在区间上为增函数。如何用x与 f(x)来描述上升的图象?如何用x与 f(x)来描述下降的图象?函数f (x)在区间上为减函数。在给定区间上任取x1,x2f(x1) < f(x2)x1<x2f(x1) > f(x2)x1<x2在给定区间上任取x1,x2 如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2,当 x1<x2时,都有 f(x1) < f(x2) ,那么就说函数f(x)在区间D上是增函数。定义:一般的,设函数 f(x)的定义域为I: 如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2,当 x1<x2 时,都有 f(x1) > f(x2) ,那么就说函数f(x) 在区间D上是减函数。二、讲授新课:判断下列说法是否正确:(1)对于二次函数f(x)=x2,因为-1,2∈ R且-1<2,
此时有f(-1)对于任意的x2>0,都有f(x2)在 [0,+∞)上是减函数。提问:你认为定义中的关键词语是什么?
答:定义域,区间,任意,都有。
例1 如图,是定义在区间[-4,3]上的函数 y= f(x)的图象,根据图象说出y= f(x)的单调区间,以及在每个单调区间上, y= f(x)是增函数还是减函数。[-4,-2),[-2,1),[1,2),[2,3)三、例题分析:证明:(条件)(论证结果)(结论)例2.证明函数 在R上是增函数.证明函数单调性的步骤:第一步:取值.即任取区间内的两个值,且x1 A组 P32.1 B组 P32.2
C组 p32.3 D组 p32.4
4、练习 :5、小结: 1 函数单调性的概念,注意其中的关键词
2 定义法证明函数单调性的步骤。
3 掌握数形结合的方法。
6、作业: 书P39习题1.3
1,2,3
?
?
此时有f(-1)
答:定义域,区间,任意,都有。
例1 如图,是定义在区间[-4,3]上的函数 y= f(x)的图象,根据图象说出y= f(x)的单调区间,以及在每个单调区间上, y= f(x)是增函数还是减函数。[-4,-2),[-2,1),[1,2),[2,3)三、例题分析:证明:(条件)(论证结果)(结论)例2.证明函数 在R上是增函数.证明函数单调性的步骤:第一步:取值.即任取区间内的两个值,且x1
C组 p32.3 D组 p32.4
4、练习 :5、小结: 1 函数单调性的概念,注意其中的关键词
2 定义法证明函数单调性的步骤。
3 掌握数形结合的方法。
6、作业: 书P39习题1.3
1,2,3
?
?
