高中数学人教A版必修1课件: 第一章 1.3.2 函数的奇偶性
文档属性
| 名称 | 高中数学人教A版必修1课件: 第一章 1.3.2 函数的奇偶性 |

|
|
| 格式 | zip | ||
| 文件大小 | 616.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-08 00:00:00 | ||
图片预览






文档简介
课件27张PPT。1.3.2 奇偶性welcome to use these PowerPoint templates, New Content design, 10 years experience
结合具体函数,了解奇偶性的含义;
学会运用函数图象理解和研究函数的性质。welcome to use these PowerPoint templates, New Content design, 10 years experience
通过实例直观感知,会描述偶(奇)函数定义,理解其图象特征;
能判断给定函数的奇偶性;
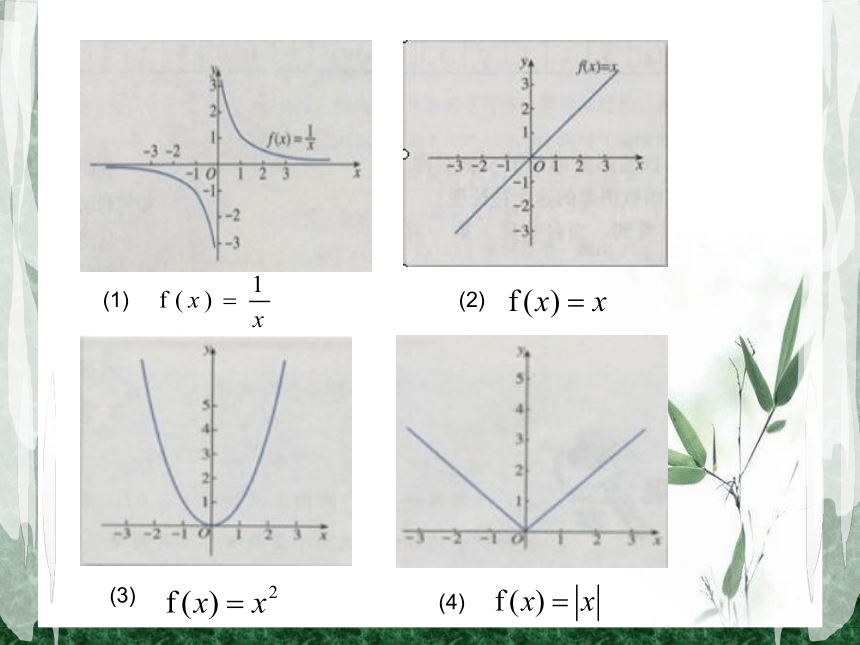
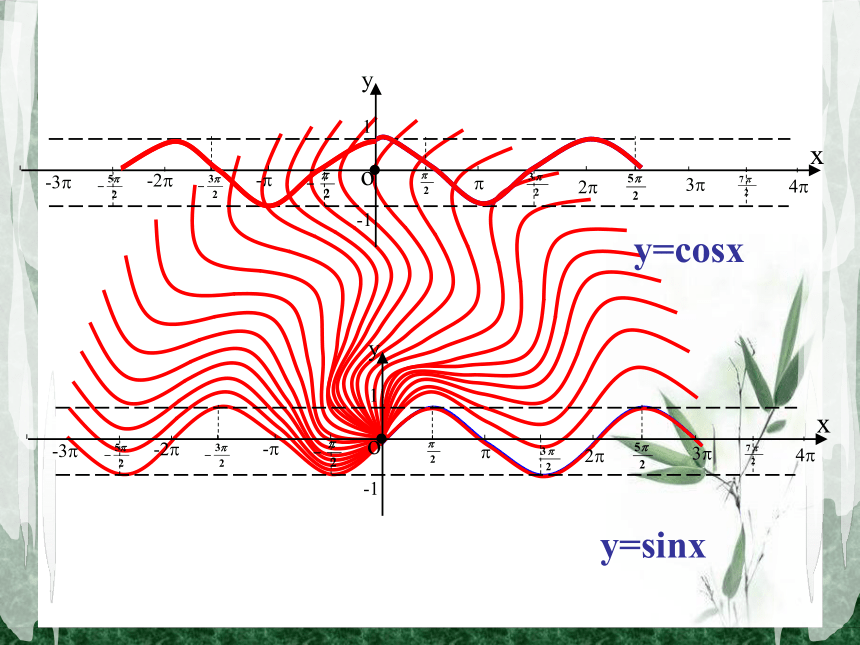
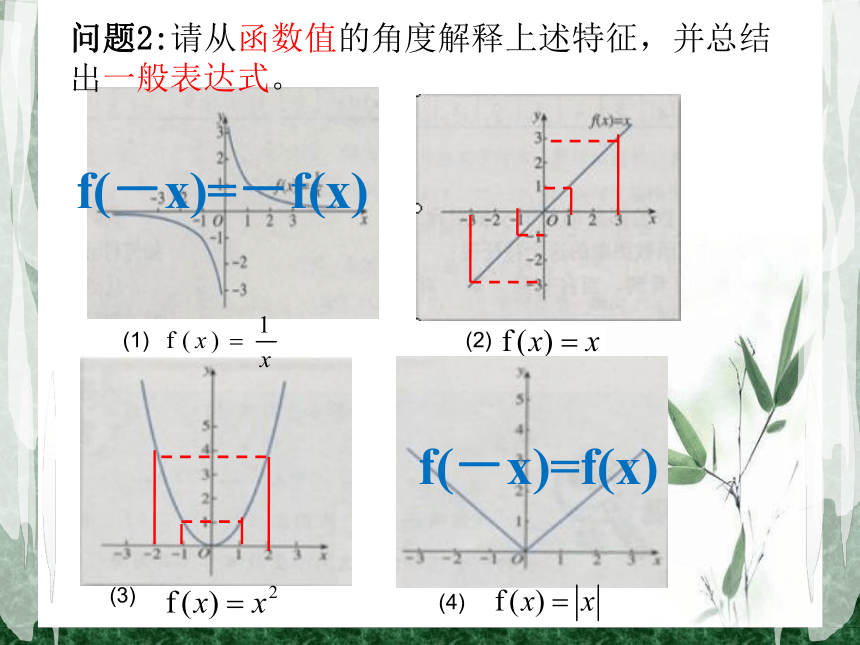
学会运用奇(偶)函数图象,研究函数的一些简单性质;(3)(4)(2)(1)问题1:请从对称性角度对以下图片进行分类,并总结其特征;y=sinxy=cosx(3)(4)(2)(1)问题2:请从函数值的角度解释上述特征,并总结出一般表达式。f(-x)=f(x)f(-x)=-f(x)问题3:请尝试概括偶函数定义,并对关键词进行解释说明;
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数. 任务一:会描述奇(偶)函数定义。
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数. (2)若对于定义域内的一些 ,使 则 是偶函数;(3)若对于定义域内的无数个 ,使
则 是偶函数;
(4)若对于定义域内的任意 ,使
则 是偶函数;
(5)若 则 不是偶函数。对于定义在 上的函数 ,判断正误:正确错误错误错误正确
问题4:类比偶函数定义,请给出奇函数定义?
问题5:请分别举出一个奇函数和一个偶函数的例子,并说明;
一般地,对于函数f(x)的定义域内的任意一个x,都有 ,那么f(x)就叫做 函数. f(-x)= -f(x)f(-x)=f(x)偶奇任务一:会描述偶(奇)函数定义。思考:请比较偶函数和奇函数的相同点和异同点,以气泡图的形式呈现。对于奇、偶函数定义的几点说明:(3)定义域关于原点对称是函数具有奇偶性的先决条件; (4)奇、偶函数定义的逆命题也成立,
即:若函数f(x)为奇函数, 则f(-x)=-f(x)成立。
若函数f(x)为偶函数, 则f(-x)= f(x) 成立。(1)如果一个函数f(x)是奇函数或偶函数,那么我们就
是说函数f(x) 具有奇偶性;(2)函数的奇偶性是相对于函数的整个定义域而言的是函数的整体性质;偶偶奇奇非奇非偶既奇又偶(7) f(x)=5 (8) f(x)=0 (9)f(x)=x+1 xxyy偶既奇又偶非奇非偶任务二:能判断函数奇偶性。例1oo问题1:函数的奇偶性有几种可能?用定义法判断函数的奇偶性的步骤,以流程图形式呈现。奇函数
偶函数
非奇非偶
既奇又偶例2-2800问题:将教材P36-----练习(2)的图象补充完整,并思考函数的奇偶性与单调性有什么区别和联系? 任务三:会运用函数图象。welcome to use these PowerPoint templates, New Content design, 10 years experience
通过实例直观感知,会描述偶(奇)函数定义,理解其图象特征;
能判断给定函数的奇偶性;
学会运用奇(偶)函数图象,研究函数的一些简单性质;谢谢!思考:函数的奇偶性与单调性有什么区别和联系?任务三:会运用函数图象。Thank you!例3.已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.解:画法略问题1:如何函数y=f(x)是奇函数,图象该如何画?问题2:函数奇偶性与单调性有什么联系?思考题:函数的奇偶性与单调性有什么联系?若f(x)为奇函数,则f(x)在[a,b]和[-b,-a]上具有相同的单调性
若f(x)为偶函数,则f(x)在[a,b]和[-b,-a]上具有相反的单调性
而函数的奇偶性是函数的整体性质;函数的单调性是函数的局部性质.判断奇偶性的方法:1.定义法2.图像法3.性质法:奇奇偶偶偶偶奇函数图象关于y轴对称.函数的奇偶性奇函数偶函数从几何上看:从代数上看:从几何上看:从代数上看:?函数图象关于原点对称.??奇偶性与单调性的关系若f(x)为奇函数,则f(x)在[a,b]和[-b,-a]上具有相同的单调性
若f(x)为偶函数,则f(x)在[a,b]和[-b,-a]上具有相反的单调性
而函数的奇偶性是函数的整体性质;函数的单调性是函数的局部性质.
结合具体函数,了解奇偶性的含义;
学会运用函数图象理解和研究函数的性质。welcome to use these PowerPoint templates, New Content design, 10 years experience
通过实例直观感知,会描述偶(奇)函数定义,理解其图象特征;
能判断给定函数的奇偶性;
学会运用奇(偶)函数图象,研究函数的一些简单性质;(3)(4)(2)(1)问题1:请从对称性角度对以下图片进行分类,并总结其特征;y=sinxy=cosx(3)(4)(2)(1)问题2:请从函数值的角度解释上述特征,并总结出一般表达式。f(-x)=f(x)f(-x)=-f(x)问题3:请尝试概括偶函数定义,并对关键词进行解释说明;
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数. 任务一:会描述奇(偶)函数定义。
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数. (2)若对于定义域内的一些 ,使 则 是偶函数;(3)若对于定义域内的无数个 ,使
则 是偶函数;
(4)若对于定义域内的任意 ,使
则 是偶函数;
(5)若 则 不是偶函数。对于定义在 上的函数 ,判断正误:正确错误错误错误正确
问题4:类比偶函数定义,请给出奇函数定义?
问题5:请分别举出一个奇函数和一个偶函数的例子,并说明;
一般地,对于函数f(x)的定义域内的任意一个x,都有 ,那么f(x)就叫做 函数. f(-x)= -f(x)f(-x)=f(x)偶奇任务一:会描述偶(奇)函数定义。思考:请比较偶函数和奇函数的相同点和异同点,以气泡图的形式呈现。对于奇、偶函数定义的几点说明:(3)定义域关于原点对称是函数具有奇偶性的先决条件; (4)奇、偶函数定义的逆命题也成立,
即:若函数f(x)为奇函数, 则f(-x)=-f(x)成立。
若函数f(x)为偶函数, 则f(-x)= f(x) 成立。(1)如果一个函数f(x)是奇函数或偶函数,那么我们就
是说函数f(x) 具有奇偶性;(2)函数的奇偶性是相对于函数的整个定义域而言的是函数的整体性质;偶偶奇奇非奇非偶既奇又偶(7) f(x)=5 (8) f(x)=0 (9)f(x)=x+1 xxyy偶既奇又偶非奇非偶任务二:能判断函数奇偶性。例1oo问题1:函数的奇偶性有几种可能?用定义法判断函数的奇偶性的步骤,以流程图形式呈现。奇函数
偶函数
非奇非偶
既奇又偶例2-2800问题:将教材P36-----练习(2)的图象补充完整,并思考函数的奇偶性与单调性有什么区别和联系? 任务三:会运用函数图象。welcome to use these PowerPoint templates, New Content design, 10 years experience
通过实例直观感知,会描述偶(奇)函数定义,理解其图象特征;
能判断给定函数的奇偶性;
学会运用奇(偶)函数图象,研究函数的一些简单性质;谢谢!思考:函数的奇偶性与单调性有什么区别和联系?任务三:会运用函数图象。Thank you!例3.已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.解:画法略问题1:如何函数y=f(x)是奇函数,图象该如何画?问题2:函数奇偶性与单调性有什么联系?思考题:函数的奇偶性与单调性有什么联系?若f(x)为奇函数,则f(x)在[a,b]和[-b,-a]上具有相同的单调性
若f(x)为偶函数,则f(x)在[a,b]和[-b,-a]上具有相反的单调性
而函数的奇偶性是函数的整体性质;函数的单调性是函数的局部性质.判断奇偶性的方法:1.定义法2.图像法3.性质法:奇奇偶偶偶偶奇函数图象关于y轴对称.函数的奇偶性奇函数偶函数从几何上看:从代数上看:从几何上看:从代数上看:?函数图象关于原点对称.??奇偶性与单调性的关系若f(x)为奇函数,则f(x)在[a,b]和[-b,-a]上具有相同的单调性
若f(x)为偶函数,则f(x)在[a,b]和[-b,-a]上具有相反的单调性
而函数的奇偶性是函数的整体性质;函数的单调性是函数的局部性质.
