高中数学人教A版必修1课件: 第一章 1.3.2 函数的奇偶性
文档属性
| 名称 | 高中数学人教A版必修1课件: 第一章 1.3.2 函数的奇偶性 |  | |
| 格式 | zip | ||
| 文件大小 | 475.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-08 12:01:37 | ||
图片预览







文档简介
课件23张PPT。学习目标1. 理解函数奇偶性的定义,掌握用定义判断和证明函数的奇偶性;
2.探究并归纳函数奇偶性的判断及其他们的图像特征;
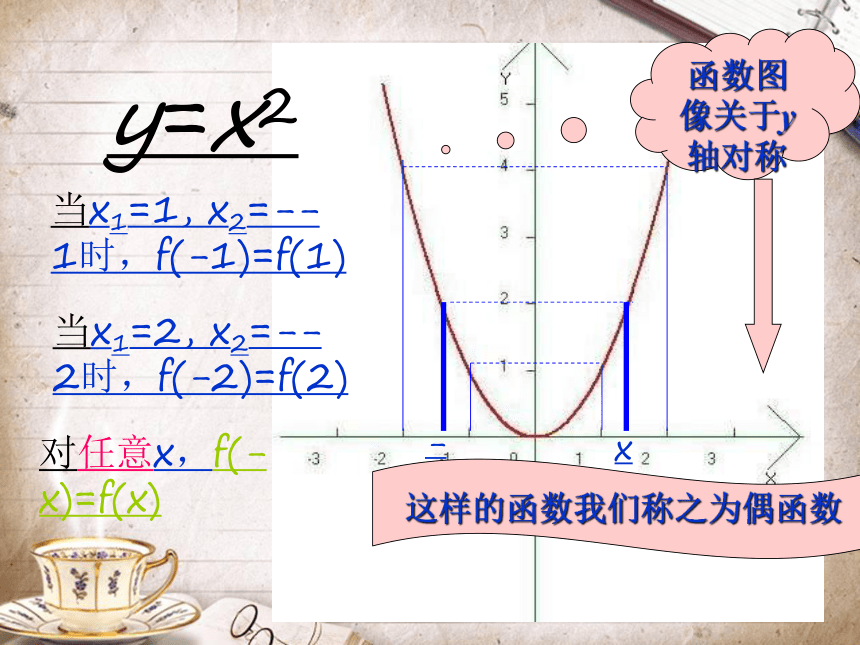
函数的奇偶性y=x2 -xx当x1=1, x2=--1时,f(-1)=f(1)
当x1=2, x2=--2时,f(-2)=f(2)
对任意x,f(-x)=f(x)
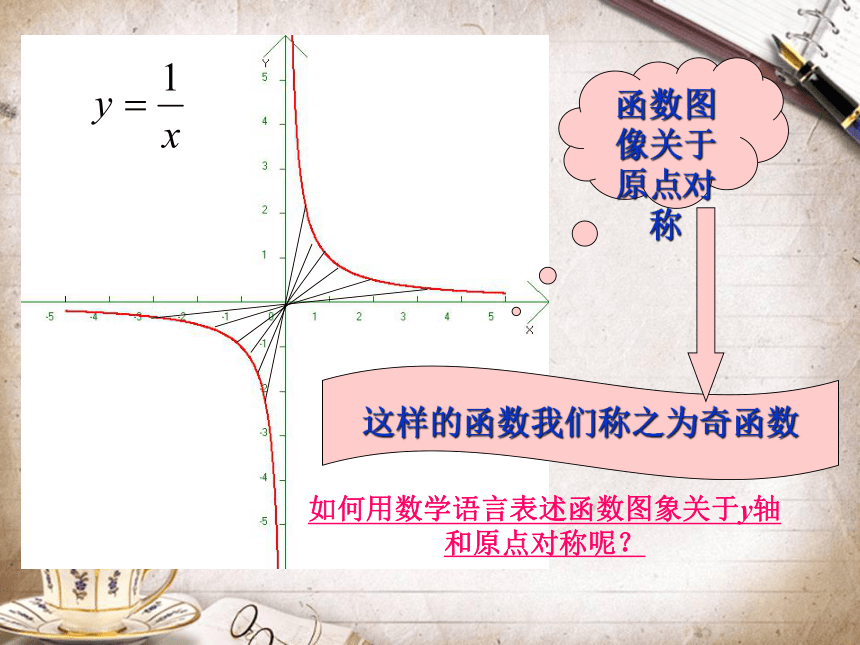
函数图像关于y轴对称这样的函数我们称之为偶函数函数图像关于原点对称这样的函数我们称之为奇函数如何用数学语言表述函数图象关于y轴和原点对称呢?偶函数定义:
如果对于函数f(x)定义域内的任意一个x,
都有f(-x)=f(x)成立,则称函数f(x)为偶函数.
图象关于Y轴对称
奇函数定义: 如果对于函数f(x)定义域内的任意一个x,
都有f(-x)=-f(x)成立,则称函数f(x)为奇函数.
图象关于原点对称
函数的奇偶性问题1:奇函数、偶函数的定义中有“任
意”二字,说明函数的奇偶性是怎样的
一个性质?与单调性有何区别? 强调定义中“任意”二字,说明函
数的奇偶性是在定义域上的一个整体性质,
它不同于函数的单调性?. 对于定义在R上的函数 f (x),下列判断是否正确?若f (-2) = f (2),则函数 f (x)是偶函数.若f (-2) ≠ f (2),则函数 f (x)不是偶函数.错。 不满足任意性对。问题2:-x与x在几何上有何关系?具有
奇偶性的函数的定义域有何特征? 奇函数与偶函数的定义域的特征是
关于原点对称. 如果一个函数是奇函数,则这个函数的图象是以坐标原点为对称中心的中心对称图形. 反之,如果一个函数的图象是以坐标原点为对称中心的中心对称图形,则这个函数是奇函数.
如果一个函数是偶函数,则它的图象是以y轴为对称轴的轴对称图形;反之,如果一个函数的图象关于y轴对称,则这个函数是偶函数. 2. 奇函数与偶函数图象的对称性.问题3:
如果f (0)=a≠0,函数f (x)可以是奇函
数吗?为什么?奇函数在X=0处若有意义,必有f (0)=0不可以例1.判断下列函数奇偶性.该函数是偶函数该函数是奇函数该函数是非奇非偶函数该函数是非奇非偶函数定义域不关于原点对称的函数都是非奇非偶函数1. 判断下列论断是否正确(错)(对)(错)(对)练 习(1)如果一个函数的定义域关于坐标原点
对称,则这个函数关于原点对称且这
个函数为奇函数;
(2)如果一个函数为偶函数,则它的定义
域关于坐标原点对称.
(3)如果一个函数定义域关于坐标原点对
称,则这个函数为偶函数;
(4)如果一个函数的图象关于y轴对称,则
这个函数为偶函数. 2.判断下列函数的奇偶性:练习:该函数是奇函数该函数是偶函数该函数是非奇非偶函数该函数是偶函数3. 如图⑴,给出了奇函数y=f (x)的局部
图象,求f (-4).4. 如图⑵,给出了偶函数y=f (x)的局部
图象,试比较f (1)与 f (3) 的大小.练 习⑴⑵例.已知函数f(x)既是奇函数又是偶函数。求证:f(x)=0证明:因为 f(x)既是奇函数又是偶函数
所以f(-x)=f(x),且f(-x)=-f(x)
所以f(x)= -f(x)
所以2f(x)=0
即f(x)=0.这样的函数有多少个呢?1、函数的奇偶性分类:
① 奇函数 ② 偶函数
③ 非奇非偶函数 ④ 既奇又偶函数
2、既奇又偶函数的表达式为:f(x)=0,x∈A,定义域A是关于原点对称的非空数集。
既奇又偶函数有无数多个。课堂小结:如果定义域关于原点对称,且对定义域内的任意一个x练习1.若奇函数在原点有定义, 则f(0)=?0练习2.判断 的奇偶性?定义域是{0},f(x)=0,是既奇又偶函数。奇偶函数的单调性奇同偶异 例 1 已知函数 y = f (x) 在R上是奇函数,而且
在(0,+∞)上是增函数,
证明 y = f (x) 在(- ∞,0)上也是增函数 .答案: (1)非奇非偶(定义域关于原点不对称).
(2)奇函数 .小结1、单调性: 定义域某区间,是函数的局部性质
奇偶性: 整个定义域, 是函数的整体性质
2、判断奇偶性的步骤和方法
(1)定义法:
①定义域是否关于原点对称?
②f(x)与±f(-x)的关系 ?
(2)图像法:
(3)性质法:练习2.设f(x)是奇函数,而且在(0,+∞)上是减函数,证f(x) 在(-∞,0)上是减函数。练习1. 设f(x)是偶函数,而且在[a,b]上是减函数,证f(x) 在[-b,-a]上是增函数。(其中0且求函数f (x),g(x)的解析式;
2.探究并归纳函数奇偶性的判断及其他们的图像特征;
函数的奇偶性y=x2 -xx当x1=1, x2=--1时,f(-1)=f(1)
当x1=2, x2=--2时,f(-2)=f(2)
对任意x,f(-x)=f(x)
函数图像关于y轴对称这样的函数我们称之为偶函数函数图像关于原点对称这样的函数我们称之为奇函数如何用数学语言表述函数图象关于y轴和原点对称呢?偶函数定义:
如果对于函数f(x)定义域内的任意一个x,
都有f(-x)=f(x)成立,则称函数f(x)为偶函数.
图象关于Y轴对称
奇函数定义: 如果对于函数f(x)定义域内的任意一个x,
都有f(-x)=-f(x)成立,则称函数f(x)为奇函数.
图象关于原点对称
函数的奇偶性问题1:奇函数、偶函数的定义中有“任
意”二字,说明函数的奇偶性是怎样的
一个性质?与单调性有何区别? 强调定义中“任意”二字,说明函
数的奇偶性是在定义域上的一个整体性质,
它不同于函数的单调性?. 对于定义在R上的函数 f (x),下列判断是否正确?若f (-2) = f (2),则函数 f (x)是偶函数.若f (-2) ≠ f (2),则函数 f (x)不是偶函数.错。 不满足任意性对。问题2:-x与x在几何上有何关系?具有
奇偶性的函数的定义域有何特征? 奇函数与偶函数的定义域的特征是
关于原点对称. 如果一个函数是奇函数,则这个函数的图象是以坐标原点为对称中心的中心对称图形. 反之,如果一个函数的图象是以坐标原点为对称中心的中心对称图形,则这个函数是奇函数.
如果一个函数是偶函数,则它的图象是以y轴为对称轴的轴对称图形;反之,如果一个函数的图象关于y轴对称,则这个函数是偶函数. 2. 奇函数与偶函数图象的对称性.问题3:
如果f (0)=a≠0,函数f (x)可以是奇函
数吗?为什么?奇函数在X=0处若有意义,必有f (0)=0不可以例1.判断下列函数奇偶性.该函数是偶函数该函数是奇函数该函数是非奇非偶函数该函数是非奇非偶函数定义域不关于原点对称的函数都是非奇非偶函数1. 判断下列论断是否正确(错)(对)(错)(对)练 习(1)如果一个函数的定义域关于坐标原点
对称,则这个函数关于原点对称且这
个函数为奇函数;
(2)如果一个函数为偶函数,则它的定义
域关于坐标原点对称.
(3)如果一个函数定义域关于坐标原点对
称,则这个函数为偶函数;
(4)如果一个函数的图象关于y轴对称,则
这个函数为偶函数. 2.判断下列函数的奇偶性:练习:该函数是奇函数该函数是偶函数该函数是非奇非偶函数该函数是偶函数3. 如图⑴,给出了奇函数y=f (x)的局部
图象,求f (-4).4. 如图⑵,给出了偶函数y=f (x)的局部
图象,试比较f (1)与 f (3) 的大小.练 习⑴⑵例.已知函数f(x)既是奇函数又是偶函数。求证:f(x)=0证明:因为 f(x)既是奇函数又是偶函数
所以f(-x)=f(x),且f(-x)=-f(x)
所以f(x)= -f(x)
所以2f(x)=0
即f(x)=0.这样的函数有多少个呢?1、函数的奇偶性分类:
① 奇函数 ② 偶函数
③ 非奇非偶函数 ④ 既奇又偶函数
2、既奇又偶函数的表达式为:f(x)=0,x∈A,定义域A是关于原点对称的非空数集。
既奇又偶函数有无数多个。课堂小结:如果定义域关于原点对称,且对定义域内的任意一个x练习1.若奇函数在原点有定义, 则f(0)=?0练习2.判断 的奇偶性?定义域是{0},f(x)=0,是既奇又偶函数。奇偶函数的单调性奇同偶异 例 1 已知函数 y = f (x) 在R上是奇函数,而且
在(0,+∞)上是增函数,
证明 y = f (x) 在(- ∞,0)上也是增函数 .答案: (1)非奇非偶(定义域关于原点不对称).
(2)奇函数 .小结1、单调性: 定义域某区间,是函数的局部性质
奇偶性: 整个定义域, 是函数的整体性质
2、判断奇偶性的步骤和方法
(1)定义法:
①定义域是否关于原点对称?
②f(x)与±f(-x)的关系 ?
(2)图像法:
(3)性质法:练习2.设f(x)是奇函数,而且在(0,+∞)上是减函数,证f(x) 在(-∞,0)上是减函数。练习1. 设f(x)是偶函数,而且在[a,b]上是减函数,证f(x) 在[-b,-a]上是增函数。(其中0
