1.3.2　函数的奇偶性

课件16张PPT。1.3　函数的基本性质
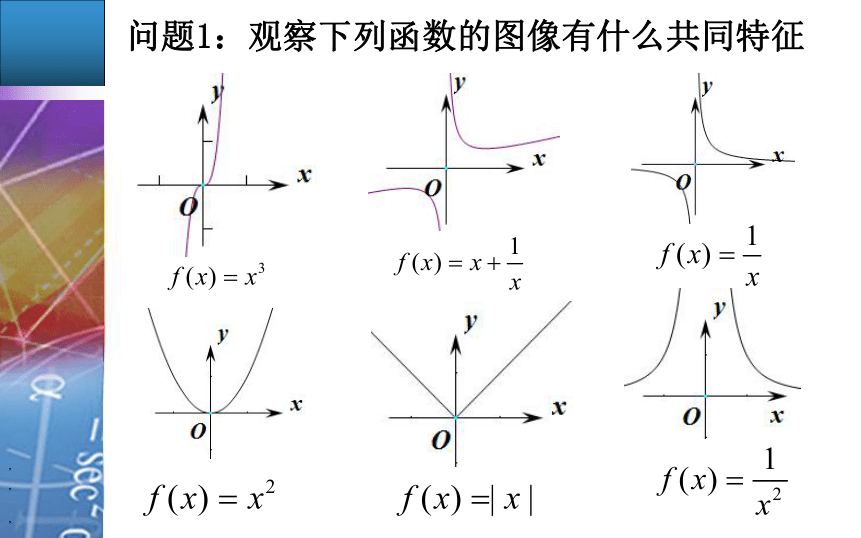
1.3.2　函数的奇偶性问题1：观察下列函数的图像有什么共同特征
， ， ， ， ， 巴黎埃菲尔铁塔北京故宫复习：什么叫做轴对称图形?
什么叫做中心对称图形?
如果把一个图形沿一条直线折起来,直线两侧部分能够互相重合,那么这个图形叫做轴对称图形. 如果一个图形绕某一点旋转180度，旋转后的
图形能和原图形完全重合，那么这个图形叫做中心
对称图形.问题2：如何用数量关系来描述函数 图像的
对称性.形成概念：一般地，如果对于 函数f(x)的定义域内任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数.探究：判断下列函数是否是偶函数：提问：（1）如何说明一个函数是偶函数？
（2）如果这个函数不是偶函数，你如何来判断？练习：判断下列函数是否是偶函数
（1）（2）（3）问题：你认为偶函数的图像有什么特点？小结：刚才我们都探究了偶函数的哪些性质？偶函数的定义判断一个函数是偶函数偶函数的图象的特点2．类比学习：请以函数 为例
对照研究偶函数的方法，用类比的方法讨论分析给出奇函数的定义并给出定义分析，判断函数是奇函数的方法及奇函数的图像特点。试一试：判断下列函数的奇偶性(1) (2) (3) (4) 提问：判断函数奇偶性的结果有哪几种？思考：（1）既是奇函数又是偶函数的函数解析式是什么？
这样的函数有多少个？（2）若y=f(x) x∈R是奇函数，则f（0）的值是什么？课堂练习2、奇函数y＝f(x)(x∈R)的图象上有一点为（a,f(a)），
则图像必过点(　　)1、函数 的奇偶性是 （ ）
A．奇函数
B. 偶函数
C.非奇非偶函数
D.既是奇函数又是偶函数 3、若f(x)为R上的偶函数，且当x∈（－∞，0）时，
f(x)=x(x-1），则当x∈（0，+∞）时，f(x)= .解析：当x∈(0，＋∞)时，－x∈(－∞，0)，
因为x∈(－∞，0)时，f(x)＝x（x-1），
所以f(－x)＝(－x)(－x－1)＝x(x+1)，
因为f(x)是定义在(－∞，＋∞)上的偶函数，
所以f(－x)＝f(x)，所以当x∈（0，+∞）时f(x)＝x(x+1).试一试偶函数f(x)(x∈R)满足：f(－4)＝f(1)＝0，且在区间[0,3]与[3，＋∞)上分别递减和递增，使f(x)＜0的自变量范围是(　　)
A．(－∞，－4)∪(4，＋∞)
B．(－4，－1)∪(1,4)
C．(－∞，－4)∪(－1,0)
D．(－∞，－4)∪(－1,0)∪(1,4)
解析：根据题目条件，想象函数图象如下：答案：B