1.2 空间几何 体的三视图
图片预览





文档简介
课件19张PPT。1.2 空间几何体的三视图 1、 本节我们将要学习如何将空间几何体用平面图形表示出来,同时能够根据平面图形想象空间几何体的形状和结构. 2、我们将在了解投影知识的基础上,学习空间几何体的三视图 3、会画简单的空间几何体(柱、锥、台、球及其组合)的三视图,能够识别三视图所描述的模型.学习目标1.光线从几何体的前面向后面正投影所得到的投影图
叫做几何体的正视图.
2.光线从几何体的左面向右面正投影所得到的投影图
叫做几何体侧视图.
3.光线从几何体的上面向下面正投影所得到的投影图
叫做几何体的俯视图.三视图 把一个空间几何体投影到一个平面上,可以获得一个平面图形.视图是指将物体按正投影向投影面投射所得到的图形.
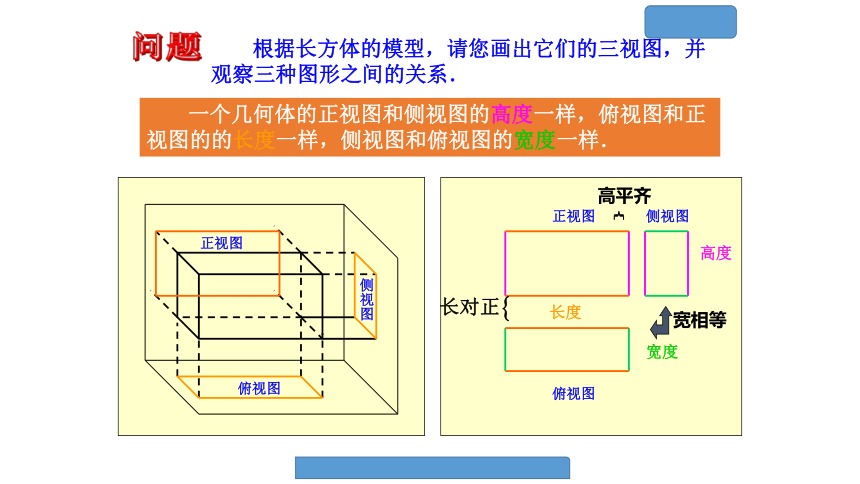
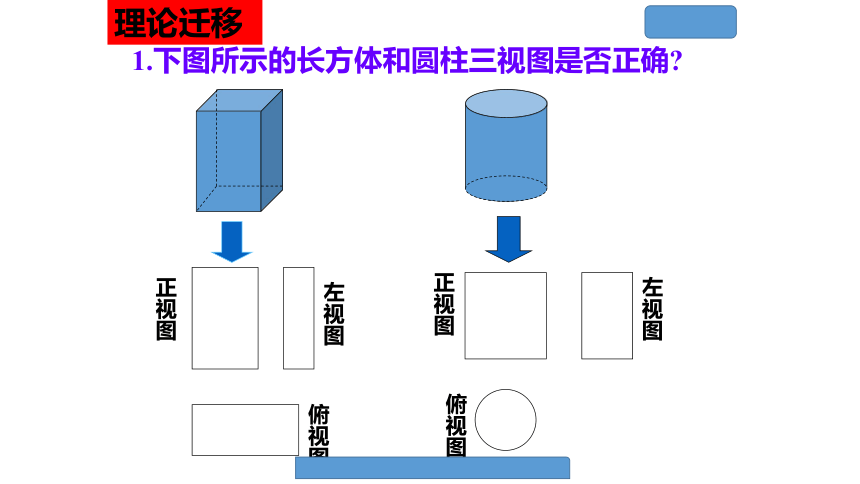
但只有一个平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影.1.三视图的概念俯视图正视图侧视图问题 根据长方体的模型,请您画出它们的三视图,并观察三种图形之间的关系. 一个几何体的正视图和侧视图的高度一样,俯视图和正视图的的长度一样,侧视图和俯视图的宽度一样.1.下图所示的长方体和圆柱三视图是否正确?理论迁移(1)分析从几何体的正前方、正左方、正上方所看到的正投影图;
(2)按照“长对正、高平齐、宽相等”作出对应的三视图;
(正视图和俯视图一样长,正视图和侧视图一样高,俯视图和侧视图一样宽)
(3)作图时能看见的轮廓线和棱用实线表示,
不能看见的用虚线表示.如何作出空间几何体的三视图?2.简单几何体的三视图请您画出下面几何体的三视图练习1注意:能看见的轮廓用实线,看不见的用虚线。请您画出圆锥的三视图理论迁移 2.如图是一个倒置的四棱柱的两种摆放,试分别画出其三视图,并比较它们的异同.正视正视能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示. 三通水管3.简单组合体的三视图画出下面这个组合图形的三视图.4.练习(1) 四棱柱(2) 圆锥与半球组成的简单组合体(3) 四棱柱与球组成的简单组合体(4) 两个圆台组成的简单组合体小结根据三视图,我们可以得到一个精确的空间几何体作业:2.根据下列三视图,想象对应的几何体.三棱柱圆台四棱柱 四棱柱与圆柱组成的简单组合体
叫做几何体的正视图.
2.光线从几何体的左面向右面正投影所得到的投影图
叫做几何体侧视图.
3.光线从几何体的上面向下面正投影所得到的投影图
叫做几何体的俯视图.三视图 把一个空间几何体投影到一个平面上,可以获得一个平面图形.视图是指将物体按正投影向投影面投射所得到的图形.
但只有一个平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影.1.三视图的概念俯视图正视图侧视图问题 根据长方体的模型,请您画出它们的三视图,并观察三种图形之间的关系. 一个几何体的正视图和侧视图的高度一样,俯视图和正视图的的长度一样,侧视图和俯视图的宽度一样.1.下图所示的长方体和圆柱三视图是否正确?理论迁移(1)分析从几何体的正前方、正左方、正上方所看到的正投影图;
(2)按照“长对正、高平齐、宽相等”作出对应的三视图;
(正视图和俯视图一样长,正视图和侧视图一样高,俯视图和侧视图一样宽)
(3)作图时能看见的轮廓线和棱用实线表示,
不能看见的用虚线表示.如何作出空间几何体的三视图?2.简单几何体的三视图请您画出下面几何体的三视图练习1注意:能看见的轮廓用实线,看不见的用虚线。请您画出圆锥的三视图理论迁移 2.如图是一个倒置的四棱柱的两种摆放,试分别画出其三视图,并比较它们的异同.正视正视能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示. 三通水管3.简单组合体的三视图画出下面这个组合图形的三视图.4.练习(1) 四棱柱(2) 圆锥与半球组成的简单组合体(3) 四棱柱与球组成的简单组合体(4) 两个圆台组成的简单组合体小结根据三视图,我们可以得到一个精确的空间几何体作业:2.根据下列三视图,想象对应的几何体.三棱柱圆台四棱柱 四棱柱与圆柱组成的简单组合体
