22.1.3 比例线段同步作业
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
22.1.3 比例线段同步作业
姓名:__________班级:__________考号:__________
一、选择题
如图,DE∥BC,分别交△ABC的边AB、AC于点D、E,,若AE=5,则EC的长度为( )
A.10 B.15 C.20 D.25
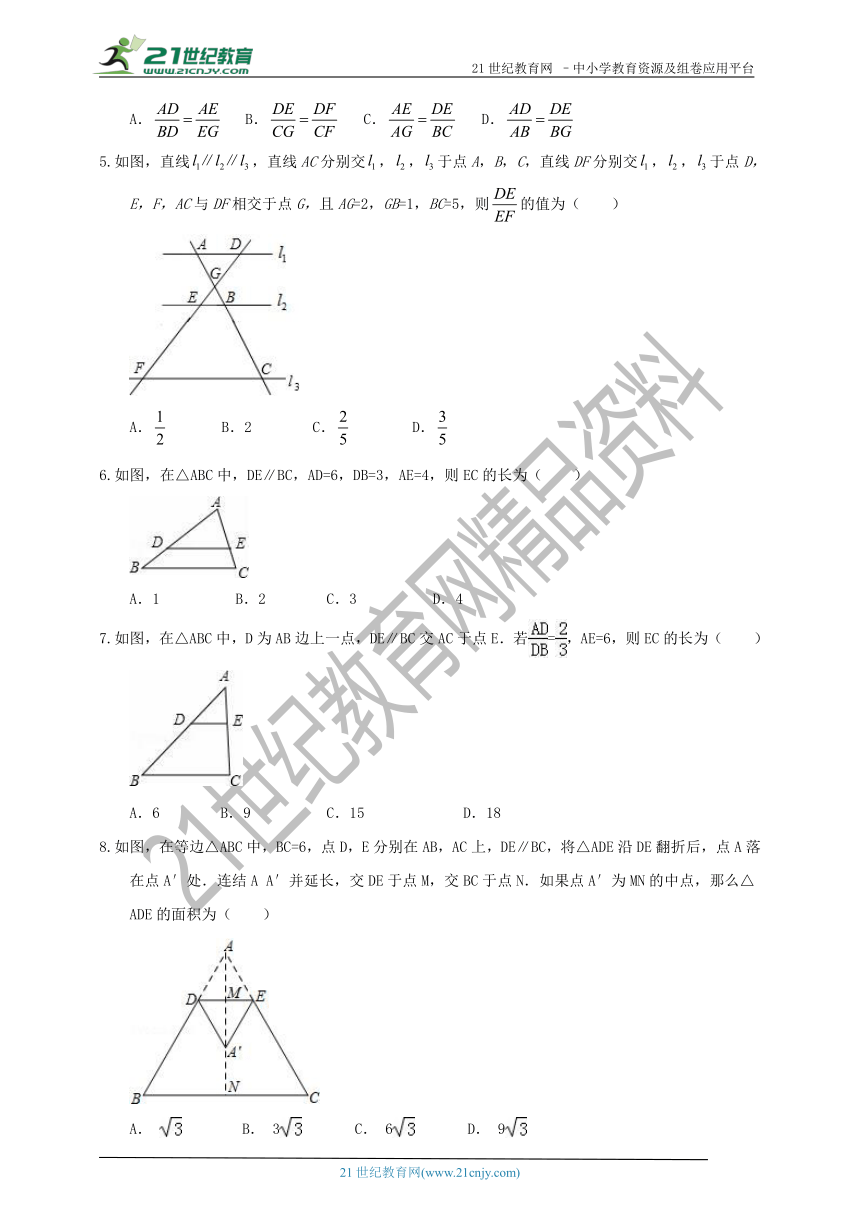
如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( )
A.4 B.4.5 C.5 D.5.5
如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则CE的长为( )
A.9 B.15 C.12 D.6
如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )
A. HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 B. C. D.
如图,直线,直线AC分别交,, HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 于点A,B,C,直线DF分别交,,于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
A. B.2 C. D. HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4
如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1 B.2 C.3 D.4
如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E.若=,AE=6,则EC的长为( )
A.6 B.9 C.15 D.18
如图,在等边△ABC中,BC=6,点D,E分别在AB,AC上,DE∥BC,将△ADE沿DE翻折后,点A落在点A′处.连结A A′并延长,交DE于点M,交BC于点N.如果点A′为MN的中点,那么△ADE的面积为( )
A. B. 3 C. 6 D. 9
二、填空题
如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC=______.
如图,在△ABC中,若DE∥BC,=,DE=4,则BC的长是 .
图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC= cm.
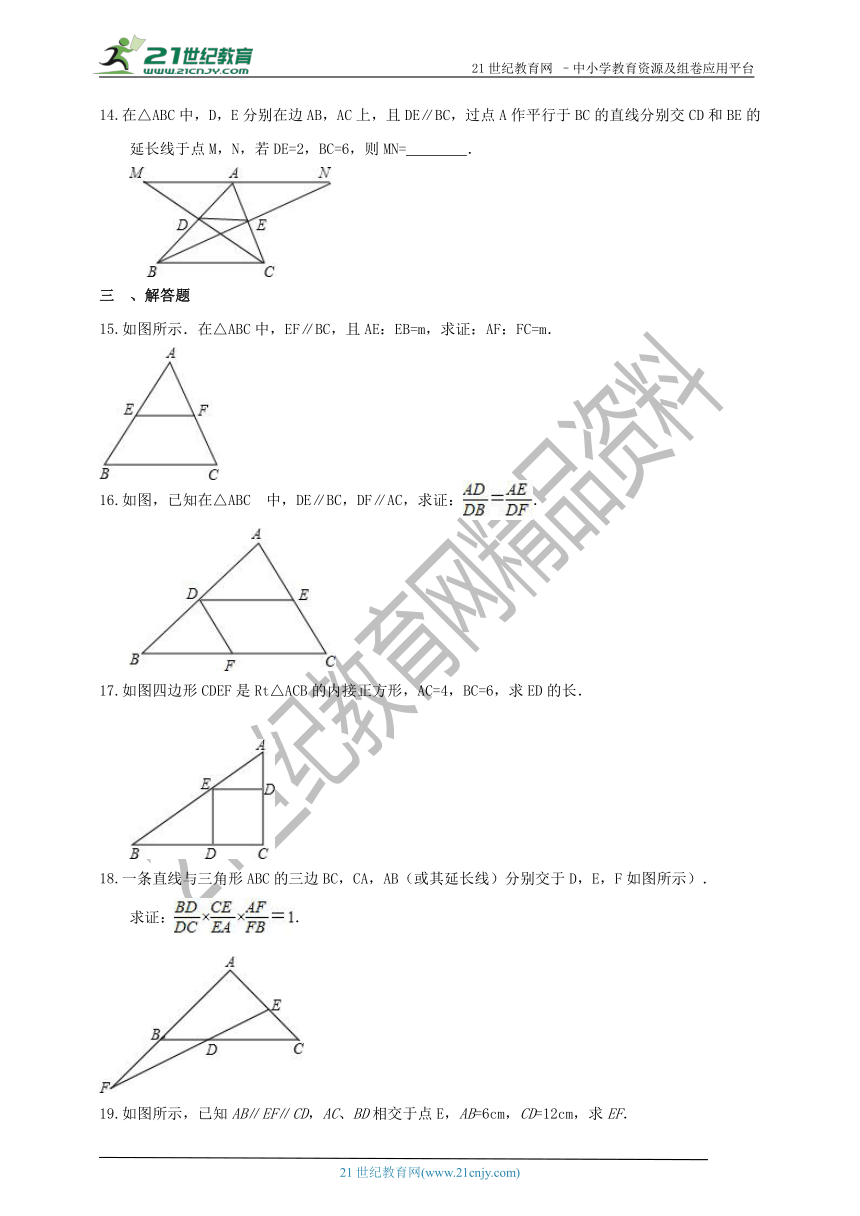
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F, =,DE=6,则EF= .
如图,△ABC中,AB=6,DE∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为 .
在△ABC中,D,E分别在边AB,AC上,且DE∥BC,过点A作平行于BC的直线分别交CD和BE的延长线于点M,N,若DE=2,BC=6,则MN= .
三 、解答题
如图所示.在△ABC中,EF∥BC,且AE:EB=m,求证:AF:FC=m.
如图,已知在△ABC 中,DE∥BC,DF∥AC,求证:.
如图四边形CDEF是Rt△ACB的内接正方形,AC=4,BC=6,求ED的长.
一条直线与三角形ABC的三边BC,CA,AB(或其延长线)分别交于D,E,F如图所示).
求证:.
如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,求EF.
如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.
(1)求证:AF⊥BE;
(2)求证:AD=3DI.
如图.在△ABC中,E是AB的中点,D是AC上的一点,且AD:DC=2:3,BD与CE交于F,S△ABC=40,求SAEFD.
答案解析
一 、选择题
【考点】平行线分线段成比例
【分析】根据平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例,由DE∥BC得到,于是可计算出AC的长,然后利用进行计算即可.
解:∵DE∥BC,
∴,
∴ HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,
∴AC=15.
∴.
故选A.
【考点】平行线分线段成比例.
【分析】直接根据平行线分线段成比例定理即可得出结论.
解:∵直线a∥b∥c,AC=4,CE=6,BD=3,
∴=,即=,解得DF=4.5.
故选B.
【点评】本题考查的是平行线分线段成比例定理,熟知三条平行线截两条直线,所得的对应线段成比例是解答此题的关键.
【考点】平行线分线段成比例
【分析】根据平行线分线段成比例定理得到,再利用比例性质由AD:DF:FB=3:2:1得 HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,则,然后把AG=15代入计算即可.
解:∵DE∥FG∥BC,
∴ HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,
而AD:DF:FB=3:2:1,
∴,
∴,
∴EC=9.
故选A.
【考点】平行线分线段成比例
【分析】利用平行线分线段成比例定理即可得到答案.
解:∵DE∥BC交GA于点E,
∴ HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,,,
A,B,D正确,
故选C.
【考点】平行线分线段成比例
【分析】根据平行线分线段成比例可得,代入计算,可求得答案.
解:∵AG=2,GB=1,
∴,
∵直线,
∴,
故选:D.
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例可得,代入计算即可解答.
解:∵DE∥BC,
∴,
即,
解得:EC=2,
故选:B.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
【考点】平行线分线段成比例.
【分析】如图,直接运用平行线分线段成比例定理列出比例式,借助已知条件求出EC,即可解决问题.
解:如图,∵DE∥BC,
∴,
∵=,AE=6,
∴EC=9.
故选B.
【点评】该题主要考查了平行线分线段成比例定理及其应用问题;运用平行线分线段成比例定理正确写出比例式是解题的关键.
8.【考点】 翻折变换(折叠问题).
【分析】利用△ADE沿DE翻折的特性求出AM=A′M,再由DE∥BC,得到=,求得AE,再求出AM,利用△ADE的面积=DE AM求解.
解:△ADE沿DE翻折后,点A落在点A′处
∴AM=A′M,
又∵A′为MN的中点,
∴AM=A′M=A′N,
∵DE∥AC,
∴=,
∵△ABC是等边三角形,BC=6,
∴BC=AC,
∴=
∴AE=2,
∵AN是△ABC的BC边上的高,中线及角平分线,
∴∠MAE=30°,
∴AM=,ME=1,
∴DE=2,
∴△ADE的面积=DE AM=××2=,
故选:A.
二 、填空题
【考点】平行线分线段成比例
【分析】由平行可得到,代入可求得EC,再利用线段的和可求得AC.
解:∵DE∥BC,
∴ HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,即,
解得,
∴,
故答案为: HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 .
【考点】平行线分线段成比例.
【分析】因为DE∥BC,可利用平行线分线段成比例定理求出BC的长.
解:∵DE∥BC,
∴=,
又∵=,
∴=,
∴=,
∴BC=10cm.
故答案为:10cm.
【考点】平行线分线段成比例.
【分析】过点A作AE⊥CE于点E,交BD于点D,根据平行线分线段成比例可得,代入计算即可解答.
解:如图,过点A作AE⊥CE于点E,交BD于点D,
∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,
∴,
即,
∴BC=12cm.
故答案为:12.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理得到=,即=,然后根据比例性质求EF.
解:∵AD∥BE∥CF,
∴=,即=,
∴EF=9.
故答案为9.
【点评】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例
【考点】旋转的性质;平行线的性质.
【分析】根据旋转可得BE=BE'=5,BD=BD',进而得到BD=BC﹣4,再根据平行线分线段成比例定理,即可得到=,即=,即可得出BC的长.
解:由旋转可得,BE=BE'=5,BD=BD',
∵D'C=4,
∴BD'=BC﹣4,即BD=BC﹣4,
∵DE∥AC,
∴=,即=,
解得BC=2+(负值已舍去),
即BC的长为2+.
故答案为:2+.
【分析】先根据平行线分线段成比例的定理求出AE:AC,AD:AB的值,从而得出CE:AC,BD:AB的值,再根据平行线分线段成比例的定理分别求出AN,AM的长,相加即可求出MN的长.
解:∵DE∥BC,DE=2,BC=6,
∴AE:AC=AD:AB=DE:BC=1:3.
∴CE:AC=2:3,BD:AB=2:3,
∵DE∥MN,
∴AN=3,AM=3,
∴MN=AN+AM=6.
故答案为:6.
三 、解答题
【分析】首先由EF∥BC可以得到AF:FC=AE:EB,而AE:EB=m,由此即可证明AF:FC=m.
证明:∵EF∥BC,
∴AF:FC=AE:EB,
∵AE:EB=m,
AF:FC=m.
【考点】平行线分线段成比例
【分析】根据DE∥BC,DF∥AC可以判定四边形DFCE是平行四边形,得到DF=EC,然后利用平行线分线段成比例定理得到AD:DB=AE:EC,从而得到结论.
证明:∵DE∥BC,
∴,
∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形,
∴DF=EC,
∴.
【考点】平行线分线段成比例
【分析】根据正方形的性质及平行线分线段成比例的性质列出方程式,解方程即可得出答案.
解:∵四边形CDEF是正方形,
∴ED∥BC,
∴
设ED=x,而AC=4,BC=6,
则,即ED=2.4.
【分析】过B引BG∥EF,交AC于G,将求证中所述线段“集中”到同一线段AC上进行证明.
证明:过B引BG∥EF,交AC于G.由平行线分线段成比例性质知
=,=,
∴××=××=1.
【考点】平行线分线段成比例
【分析】根据平行线分线段成比例定理可得 HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,然后求出,再利用平行线分线段成比例定理解答即可.
解:∵AB∥CD,
∴,
∴,
∵AB∥EF,
∴,
即,
解得EF=4cm.
【考点】翻折变换(折叠问题);全等三角形的判定与性质;平行线分线段成比例.
【分析】(1)根据翻折的性质和SAS证明△ABE与△ACF全等,利用全等三角形的性质得出∠AGB=90°证明即可;
(2)作IC的中点M,利用AAS证明△AEH与△FDH全等,再利用全等三角形的性质和中位线的性质解答即可.
证明:(1)∵在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,
∴AD=BD=CD,∠ACB=45°,
∵在△ADC中,AD=DC,DE⊥AC,
∴AE=CE,
∵△CDE沿直线BC翻折到△CDF,
∴△CDE≌△CDF,
∴CF=CE,∠DCF=∠ACB=45°,
∴CF=AE,∠ACF=∠DCF+∠ACB=90°,
在△ABE与△ACF中,,
∴△ABE≌△ACF(SAS),
∴∠ABE=∠FAC,
∵∠BAG+∠CAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE;
(2)作IC的中点M,连接EM,由(1)∠DEC=∠ECF=∠CFD=90°
∴四边形DECF是正方形,
∴EC∥DF,EC=DF,
∴∠EAH=∠HFD,AE=DF,
在△AEH与△FDH中,
∴△AEH≌△FDH(AAS),
∴EH=DH,
∵∠BAG+∠CAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE,
∵M是IC的中点,E是AC的中点,
∴EM∥AI,
∴,
∴DI=IM,
∴CD=DI+IM+MC=3DI,
∴AD=3DI.
【点评】此题考查翻折问题,关键是利用SAS和AAS证明三角形全等,再利用全等三角形的性质进行分析解答.
【分析】四边形AEFD可分割为△AED与△DEF.从E是AB中点及D分AC为2:3的条件看,△AED的面积不难推知,关键是如何推求△DEF的面积.为此,需通过添加辅助线的办法,寻求△DEF的面积与已知面积的关系.
解:取AD的中点G,并连接EG在△ABD中,E是AB的中点,
由题知EG∥BD.又CD:DG=3:1,
∴在△CEG中,CF:FE=CD:DG=3:1,
∴S△DFC:S△DFE=3:1.
设S△DEF=x,则S△DFC=3x,S△DEC=4x.
由于AD:DC=2:3,
∴S△EAD:S△ECD=2:3,
∴S△EAD=S△DEC=x,
S△ACE=x+4x=x,
又因为E是AB中点,
所以S△ACE=S△ABC=20,
∴x=20,
解得x=3,即S△DEF=3,
∴S△ADE=x=8,
∴S AEFD=S△ADE+S△DEF=8+3=11.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
22.1.3 比例线段同步作业
姓名:__________班级:__________考号:__________
一、选择题
如图,DE∥BC,分别交△ABC的边AB、AC于点D、E,,若AE=5,则EC的长度为( )
A.10 B.15 C.20 D.25
如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( )
A.4 B.4.5 C.5 D.5.5
如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则CE的长为( )
A.9 B.15 C.12 D.6
如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )
A. HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 B. C. D.
如图,直线,直线AC分别交,, HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 于点A,B,C,直线DF分别交,,于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
A. B.2 C. D. HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4
如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1 B.2 C.3 D.4
如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E.若=,AE=6,则EC的长为( )
A.6 B.9 C.15 D.18
如图,在等边△ABC中,BC=6,点D,E分别在AB,AC上,DE∥BC,将△ADE沿DE翻折后,点A落在点A′处.连结A A′并延长,交DE于点M,交BC于点N.如果点A′为MN的中点,那么△ADE的面积为( )
A. B. 3 C. 6 D. 9
二、填空题
如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC=______.
如图,在△ABC中,若DE∥BC,=,DE=4,则BC的长是 .
图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC= cm.
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F, =,DE=6,则EF= .
如图,△ABC中,AB=6,DE∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为 .
在△ABC中,D,E分别在边AB,AC上,且DE∥BC,过点A作平行于BC的直线分别交CD和BE的延长线于点M,N,若DE=2,BC=6,则MN= .
三 、解答题
如图所示.在△ABC中,EF∥BC,且AE:EB=m,求证:AF:FC=m.
如图,已知在△ABC 中,DE∥BC,DF∥AC,求证:.
如图四边形CDEF是Rt△ACB的内接正方形,AC=4,BC=6,求ED的长.
一条直线与三角形ABC的三边BC,CA,AB(或其延长线)分别交于D,E,F如图所示).
求证:.
如图所示,已知AB∥EF∥CD,AC、BD相交于点E,AB=6cm,CD=12cm,求EF.
如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.
(1)求证:AF⊥BE;
(2)求证:AD=3DI.
如图.在△ABC中,E是AB的中点,D是AC上的一点,且AD:DC=2:3,BD与CE交于F,S△ABC=40,求SAEFD.
答案解析
一 、选择题
【考点】平行线分线段成比例
【分析】根据平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例,由DE∥BC得到,于是可计算出AC的长,然后利用进行计算即可.
解:∵DE∥BC,
∴,
∴ HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,
∴AC=15.
∴.
故选A.
【考点】平行线分线段成比例.
【分析】直接根据平行线分线段成比例定理即可得出结论.
解:∵直线a∥b∥c,AC=4,CE=6,BD=3,
∴=,即=,解得DF=4.5.
故选B.
【点评】本题考查的是平行线分线段成比例定理,熟知三条平行线截两条直线,所得的对应线段成比例是解答此题的关键.
【考点】平行线分线段成比例
【分析】根据平行线分线段成比例定理得到,再利用比例性质由AD:DF:FB=3:2:1得 HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,则,然后把AG=15代入计算即可.
解:∵DE∥FG∥BC,
∴ HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,
而AD:DF:FB=3:2:1,
∴,
∴,
∴EC=9.
故选A.
【考点】平行线分线段成比例
【分析】利用平行线分线段成比例定理即可得到答案.
解:∵DE∥BC交GA于点E,
∴ HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,,,
A,B,D正确,
故选C.
【考点】平行线分线段成比例
【分析】根据平行线分线段成比例可得,代入计算,可求得答案.
解:∵AG=2,GB=1,
∴,
∵直线,
∴,
故选:D.
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例可得,代入计算即可解答.
解:∵DE∥BC,
∴,
即,
解得:EC=2,
故选:B.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
【考点】平行线分线段成比例.
【分析】如图,直接运用平行线分线段成比例定理列出比例式,借助已知条件求出EC,即可解决问题.
解:如图,∵DE∥BC,
∴,
∵=,AE=6,
∴EC=9.
故选B.
【点评】该题主要考查了平行线分线段成比例定理及其应用问题;运用平行线分线段成比例定理正确写出比例式是解题的关键.
8.【考点】 翻折变换(折叠问题).
【分析】利用△ADE沿DE翻折的特性求出AM=A′M,再由DE∥BC,得到=,求得AE,再求出AM,利用△ADE的面积=DE AM求解.
解:△ADE沿DE翻折后,点A落在点A′处
∴AM=A′M,
又∵A′为MN的中点,
∴AM=A′M=A′N,
∵DE∥AC,
∴=,
∵△ABC是等边三角形,BC=6,
∴BC=AC,
∴=
∴AE=2,
∵AN是△ABC的BC边上的高,中线及角平分线,
∴∠MAE=30°,
∴AM=,ME=1,
∴DE=2,
∴△ADE的面积=DE AM=××2=,
故选:A.
二 、填空题
【考点】平行线分线段成比例
【分析】由平行可得到,代入可求得EC,再利用线段的和可求得AC.
解:∵DE∥BC,
∴ HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,即,
解得,
∴,
故答案为: HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 .
【考点】平行线分线段成比例.
【分析】因为DE∥BC,可利用平行线分线段成比例定理求出BC的长.
解:∵DE∥BC,
∴=,
又∵=,
∴=,
∴=,
∴BC=10cm.
故答案为:10cm.
【考点】平行线分线段成比例.
【分析】过点A作AE⊥CE于点E,交BD于点D,根据平行线分线段成比例可得,代入计算即可解答.
解:如图,过点A作AE⊥CE于点E,交BD于点D,
∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,
∴,
即,
∴BC=12cm.
故答案为:12.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理得到=,即=,然后根据比例性质求EF.
解:∵AD∥BE∥CF,
∴=,即=,
∴EF=9.
故答案为9.
【点评】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例
【考点】旋转的性质;平行线的性质.
【分析】根据旋转可得BE=BE'=5,BD=BD',进而得到BD=BC﹣4,再根据平行线分线段成比例定理,即可得到=,即=,即可得出BC的长.
解:由旋转可得,BE=BE'=5,BD=BD',
∵D'C=4,
∴BD'=BC﹣4,即BD=BC﹣4,
∵DE∥AC,
∴=,即=,
解得BC=2+(负值已舍去),
即BC的长为2+.
故答案为:2+.
【分析】先根据平行线分线段成比例的定理求出AE:AC,AD:AB的值,从而得出CE:AC,BD:AB的值,再根据平行线分线段成比例的定理分别求出AN,AM的长,相加即可求出MN的长.
解:∵DE∥BC,DE=2,BC=6,
∴AE:AC=AD:AB=DE:BC=1:3.
∴CE:AC=2:3,BD:AB=2:3,
∵DE∥MN,
∴AN=3,AM=3,
∴MN=AN+AM=6.
故答案为:6.
三 、解答题
【分析】首先由EF∥BC可以得到AF:FC=AE:EB,而AE:EB=m,由此即可证明AF:FC=m.
证明:∵EF∥BC,
∴AF:FC=AE:EB,
∵AE:EB=m,
AF:FC=m.
【考点】平行线分线段成比例
【分析】根据DE∥BC,DF∥AC可以判定四边形DFCE是平行四边形,得到DF=EC,然后利用平行线分线段成比例定理得到AD:DB=AE:EC,从而得到结论.
证明:∵DE∥BC,
∴,
∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形,
∴DF=EC,
∴.
【考点】平行线分线段成比例
【分析】根据正方形的性质及平行线分线段成比例的性质列出方程式,解方程即可得出答案.
解:∵四边形CDEF是正方形,
∴ED∥BC,
∴
设ED=x,而AC=4,BC=6,
则,即ED=2.4.
【分析】过B引BG∥EF,交AC于G,将求证中所述线段“集中”到同一线段AC上进行证明.
证明:过B引BG∥EF,交AC于G.由平行线分线段成比例性质知
=,=,
∴××=××=1.
【考点】平行线分线段成比例
【分析】根据平行线分线段成比例定理可得 HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,然后求出,再利用平行线分线段成比例定理解答即可.
解:∵AB∥CD,
∴,
∴,
∵AB∥EF,
∴,
即,
解得EF=4cm.
【考点】翻折变换(折叠问题);全等三角形的判定与性质;平行线分线段成比例.
【分析】(1)根据翻折的性质和SAS证明△ABE与△ACF全等,利用全等三角形的性质得出∠AGB=90°证明即可;
(2)作IC的中点M,利用AAS证明△AEH与△FDH全等,再利用全等三角形的性质和中位线的性质解答即可.
证明:(1)∵在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,
∴AD=BD=CD,∠ACB=45°,
∵在△ADC中,AD=DC,DE⊥AC,
∴AE=CE,
∵△CDE沿直线BC翻折到△CDF,
∴△CDE≌△CDF,
∴CF=CE,∠DCF=∠ACB=45°,
∴CF=AE,∠ACF=∠DCF+∠ACB=90°,
在△ABE与△ACF中,,
∴△ABE≌△ACF(SAS),
∴∠ABE=∠FAC,
∵∠BAG+∠CAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE;
(2)作IC的中点M,连接EM,由(1)∠DEC=∠ECF=∠CFD=90°
∴四边形DECF是正方形,
∴EC∥DF,EC=DF,
∴∠EAH=∠HFD,AE=DF,
在△AEH与△FDH中,
∴△AEH≌△FDH(AAS),
∴EH=DH,
∵∠BAG+∠CAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE,
∵M是IC的中点,E是AC的中点,
∴EM∥AI,
∴,
∴DI=IM,
∴CD=DI+IM+MC=3DI,
∴AD=3DI.
【点评】此题考查翻折问题,关键是利用SAS和AAS证明三角形全等,再利用全等三角形的性质进行分析解答.
【分析】四边形AEFD可分割为△AED与△DEF.从E是AB中点及D分AC为2:3的条件看,△AED的面积不难推知,关键是如何推求△DEF的面积.为此,需通过添加辅助线的办法,寻求△DEF的面积与已知面积的关系.
解:取AD的中点G,并连接EG在△ABD中,E是AB的中点,
由题知EG∥BD.又CD:DG=3:1,
∴在△CEG中,CF:FE=CD:DG=3:1,
∴S△DFC:S△DFE=3:1.
设S△DEF=x,则S△DFC=3x,S△DEC=4x.
由于AD:DC=2:3,
∴S△EAD:S△ECD=2:3,
∴S△EAD=S△DEC=x,
S△ACE=x+4x=x,
又因为E是AB中点,
所以S△ACE=S△ABC=20,
∴x=20,
解得x=3,即S△DEF=3,
∴S△ADE=x=8,
∴S AEFD=S△ADE+S△DEF=8+3=11.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
