22.3 相似三角形的性质(1)同步作业
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
22.3 相似三角形的性质(1)同步作业
姓名:__________班级:__________考号:__________
一、选择题
△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是( )
A.27 B.12 C.18 D.20
已知△ABC与△DEF相似且面积比为4:1,则△ABC与△DEF的对应边上的高之比为( )
A.4:1 B.1:4 C.16:1 D.2:1
相似三角形的最短边分别是5cm和3cm,它们的面积之差为,那么小三角形的面积为( )
A. B. C. D.
如图,△ABC∽△DEF,相似比为1:2.若BC=1,则EF的长是( )
A.1 B.2 C.3 D.4
若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )
A.1:2 B.2:1 C.1:4 D.4:1
一个三角形三边之比为3:5:7,与它相似的三角形的最长边为21cm,则其余两边之和为( )
A.24cm B.21cm C.13cm D.9cm
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
A. B. C. D.
如果两个相似三角形对应角平分线的比为16:25,那么它们的面积比为( )
A、4:5 B、16:25 C、196:225 D、256:625
二、填空题
已知△ABC∽△DEF,△ABC与△DEF的相似比为4:1,则△ABC与△DEF对应边上的高之比为______.
如图,已知△ABC∽△DEF,且相似比为k,则k=________,直线y=kx+k的图象必经过________象限.
已知△ABC∽△A′B′C′,∠A=50°,则∠A的对应角∠A′=________度.
两个三角形相似,其中一个三角形的两个内角是40°、60°.那么另一个三角形的最大角是________度,最小角是________度.
如图,矩形ABCD两邻边分别为3、4,点P是矩形一边上任意一点,则点P到两条对角线AC、BD的距离之和PE+PF为_____________.
矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间为_________________
三、解答题
两个相似三角形一组对应边的长分别是24cm和12cm,若他们周长的和是240cm,求这两个三角形的周长.
如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
如图,已知△ABC中,AB=8,BC=7,AC=6,点D、E分别在AB、AC上,如果以A、D、E为顶点的三角形和△ABC相似,且相似比为 ,试求AD、AE的长.
已知:如图,△ABC∽△ADE , AE:EC=5:3,BC=6cm,∠A=40°,∠C=45°.
(1)求∠ADE的大小;
(2)求DE的长.
如图,点D、E分别在△ABC的边AB、AC上,且AB=9,AC=6,AD=3,若使△ADE与△ABC相似,求AE的长.
(1)某学校“智慧方园”数学社团遇到这样一个题目:
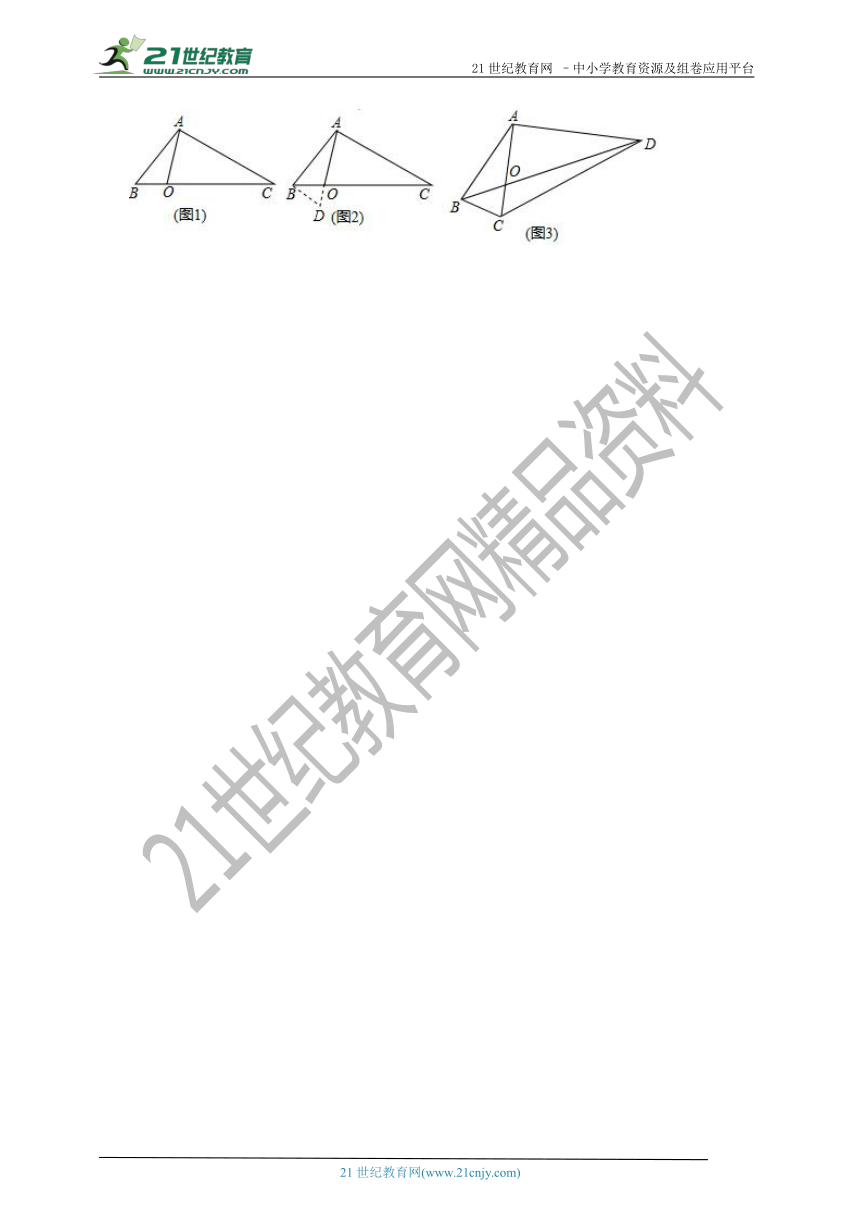
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
答案解析
一 、选择题
【考点】相似三角形的性质
【分析】设另一个三角形最短的一边是x,根据相似三角形对应边成比例即可得出结论.
解:设另一个三角形最短的一边是x,
∵△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,
∴,
解得x=18.
故选C.
【考点】相似三角形的性质
【分析】由△ABC与△DEF相似且面积比为4:1,根据相似三角形对应的面积比等于相似比的平方,即可求得△ABC与△DEF的相似比,又由相似三角形对应边上的高的比等于相似比即可求得答案.
解:∵△ABC与△DEF相似且面积比为4:1,
∴△ABC与△DEF的相似比为2:1,
∴△ABC与△DEF的对应边上的高之比2:1.
故选D.
【考点】相似三角形的性质
【分析】根据相似三角形面积的比等于相似比的平方,可求小三角形的面积为.
解:根据题意两个三角形的相似比是5:3,面积比就是25:9,
大小面积相差16份,所以每份的面积是32÷16=2(),所以小三角形的面积为2×9=18().
故选D.
【考点】相似三角形的性质
【分析】根据相似三角形对应边的比等于相似比即可求解.
解:∵△ABC∽△DEF,相似比为1:2,
∴,
∴EF=2BC=2.
故选:B.
【考点】相似三角形的性质
【分析】根据相似三角形面积的比等于相似比的平方计算即可得解.
解:∵△ABC∽△A′B′C′,相似比为1:2,
∴△ABC与△A′B′C′的面积的比为1:4.
故选:C.
【考点】相似三角形的性质
【分析】根据相似三角形对应边的比相等解答即可.
解:设其余两边的长分别是xcm,ycm,
由题意得x:y:21=3:5:7,
解得x=9,y=15,
故其余两边长的和为9+15=24(cm).
故选A.
【考点】相似三角形的性质AD
【分析】根据相似三角形的对应边成比例进行判断,要注意相似三角形的对应边和对应角.
解:∵△ABC∽△DBA,
∴;
∴,
;
故选AD.
【考点】相似三角形的性质
【分析】相似三角形对应角平分线的比等于相似比,面积比等于相似比的平方,即面积的比等于对应角平分线的比的平方.
解::根据两个相似三角形对应角平分线的比等于相似比,面积比等于相似比的平方,∴ ( http: / / www. / " \o "中国教育出版网\" )
它们的面积比为256:625.
故选:D.
二 、填空题
【考点】相似三角形的性质
【分析】根据相似三角形的对应边上的高之比等于相似比得出即可.
解:∵△ABC∽△DEF,△ABC与△DEF的相似比为4:1,
∴△ABC与△DEF对应边上的高之比是4:1,
故答案为:4:1.
【考点】相似三角形的性质
【分析】根据相似比的定义得出 =k , 推出c=(a+b)k , b=(a+c)k , a=(c+b)k , 求出k的值,即可求出答案.
解:k= = = ,
∴ =k ,
∴c=(a+b)k ,
b=(a+c)k ,
a=(c+b)k ,
相加得:(a+b+c)=2k(a+b+c),
当a+b+c=0时,k= = =-1,
∵相似比是k , ∴k=-1舍去;
当a+b+c≠0时,k= ,此时y= x+ 图象经过一、二、三象限;
故答案为: ,一、二、三.
【考点】相似三角形的性质
【分析】根据相似三角形的对应角相等解答.
解:∵△ABC∽△A′B′C′,∠A=50°,
∴∠A′=50度.
【考点】相似三角形的性质
【分析】由一个三角形的两个内角是40°、60°,根据三角形的内角各等于180°,求得第三个内角的度数,又由两个三角形相似,根据相似三角形的对应角相等,可求得答案.解答此题的关键是注意相似三角形的对应角相等.
解:∵一个三角形的两个内角是40°、60°.
∴另一个内角为:180°-40°-60°=80°,
∵两个三角形相似,
∴另一个三角形的最大角是80°,最小角是40°.
故答案为:80,40.
【考点】相似三角形的性质;矩形的性质
【分析】首先设未知线段为未知数,然后根据矩形的性质求出相似三角形,进而求解.
解:设PE=x,PF=a,PB=y.
∵∠PBF=∠ABD,∠PFB=∠DAB
∴△ABD∽△FBP,
∴,
同理可证,
∴a+x=×3=.
故答案为:.
【考点】相似三角形的性质,等腰三角形的性质,矩形的性质
【分析】由△PBE∽△DBC,可得∠PBE=∠DBC,继而可确定点P在BD上,然后再根据△APD是等腰三角形,分DP=DA、AP=DP两种情况进行讨论即可得.
解:∵四边形ABCD是矩形,∴∠BAD=∠C=90°,CD=AB=6,∴BD=10,
∵△PBE∽△DBC,
∴∠PBE=∠DBC,∴点P在BD上,
如图1,当DP=DA=8时,BP=2,
∵△PBE∽△DBC,
∴PE:CD=PB:DB=2:10,
∴PE:6=2:10,
∴PE=1.2;
如图2,当AP=DP时,此时P为BD中点,
∵△PBE∽△DBC,
∴PE:CD=PB:DB=1:2,
∴PE:6=1:2,
∴PE=3;
综上,PE的长为1.2或3,
故答案为:1.2或3.
【点睛】本题考查了相似三角形的性质,等腰三角形的性质,矩形的性质等,确定出点P在线段BD上是解题的关键.
15.【分析】首先设运动了ts,根据题意得:AP=2tcm,CQ=3tcm,然后分别从当△APQ∽△ABC与当△APQ∽△ACB时去分析求解即可求得答案.
解:设运动了ts,
根据题意得:AP=2tcm,CQ=3tcm,
则AQ=AC-CQ=16-3t(cm),
当△APQ∽△ABC时,,
即,
解得:t=;
当△APQ∽△ACB时,,
即,
解得:t=4;
故当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是:s或4s.
三 、解答题
【考点】相似三角形的性质
【分析】设两个三角形的周长分别为x、y,根据相似三角形周长的比等于对应边的比列出方程,然后求解即可.
解:设两个三角形的周长分别为x、y,
根据题意得,,
∴,
∵他们周长的和是240cm,
∴,
解得y=80,
x=2×80=160,
∴这两个三角形的周长分别为80cm和160cm.
【考点】相似三角形的性质
【分析】先根据勾股定理求出BE的长,再根据相似三角形的对应边成比例即可求出EF的长.
解:∵四边形ABCD是矩形,
∴∠BAE=90°,
∵AB=6,AE=9,
∴,
∵△ABE∽△DEF,
∴,即,
解得.
【考点】相似三角形的性质
【分析】利用三角形相似的性质分△ABC∽△ADE和△ABC∽△AED两种情况讨论即可求得AD、AE的长.
解:当△ABC∽△ADE时,相似比为 , = = ,
即: = = ,
解得:AD=2,AE=1.5;
当△ABC∽△AED时,
= = ,
即: = = ,
解得:AD=1.5,AE=2.
【考点】相似三角形的性质
【分析】先由三角形的内角和是180°求得∠ABC=95°;再由相似三角形的对应角相等得出∠ADE=∠ABC , 最后由等量代换求得∠ADE的大小;由AE:EC=5:3求得AE:AC=5:8,再根据相似三角形的对应边成比例求得DE的长度.此题主要考查了相似三角形的性质:相似三角形的对应角相等,对应边成比例.
(1)解:在△ABC中,∠A=40°,∠C=45°,
∴∠ABC=180°-40°-45°=95°;
又∵△ABC∽△ADE ,
∴∠ADE=∠ABC(相似三角形的对应角相等),
∴∠ADE =95°;
(2)解:∵AE:EC=5:3,
∴AE:AC=5:8;
又∵△ABC∽△ADE , BC=6cm,
∴ ,即
∴DE= cm.
【考点】相似三角形的性质
【分析】由于△ADE与△ABC相似,但其对应角不能确定,所以应分两种情况进行讨论.
解::①若∠AED对应∠B时,
= ,即 = ,
解得AE= ;
②当∠ADE对应∠B时,
= ,即 = ,
解得AE=2.
所以AE的长为2或 .
【考点】相似三角形的性质,等腰三角形的判定与性质,勾股定理,平行线的性质
【分析】(1)根据平行线的性质可得出∠ADB=∠OAC=75°,结合∠BOD=∠COA可得出△BOD∽△COA,利用相似三角形的性质可求出OD的值,进而可得出AD的值,由三角形内角和定理可得出∠ABD=75°=∠ADB,由等角对等边可得出AB=AD=4,此题得解;
(2)过点B作BE∥AD交AC于点E,同(1)可得出AE=4,在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解.
解:(1)∵BD∥AC,
∴∠ADB=∠OAC=75°.
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴==.
又∵AO=,
∴OD=AO=,
∴AD=AO+OD=4.
∵∠BAD=30°,∠ADB=75°,
∴∠ABD=180°﹣∠BAD﹣∠ADB=75°=∠ADB,
∴AB=AD=4.
故答案为:75;4.
(2)过点B作BE∥AD交AC于点E,如图所示.
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°.
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴==.
∵BO:OD=1:3,
∴==.
∵AO=3,
∴EO=,
∴AE=4.
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
∴AB=2BE.
在Rt△AEB中,BE2+AE2=AB2,即(4)2+BE2=(2BE)2,
解得:BE=4,
∴AB=AC=8,AD=12.
在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,
解得:CD=4.
【点评】本题考查了相似三角形的性质、等腰三角形的判定与性质、勾股定理以及平行线的性质,解题的关键是:(1)利用相似三角形的性质求出OD的值;(2)利用勾股定理求出BE、CD的长度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
22.3 相似三角形的性质(1)同步作业
姓名:__________班级:__________考号:__________
一、选择题
△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是( )
A.27 B.12 C.18 D.20
已知△ABC与△DEF相似且面积比为4:1,则△ABC与△DEF的对应边上的高之比为( )
A.4:1 B.1:4 C.16:1 D.2:1
相似三角形的最短边分别是5cm和3cm,它们的面积之差为,那么小三角形的面积为( )
A. B. C. D.
如图,△ABC∽△DEF,相似比为1:2.若BC=1,则EF的长是( )
A.1 B.2 C.3 D.4
若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )
A.1:2 B.2:1 C.1:4 D.4:1
一个三角形三边之比为3:5:7,与它相似的三角形的最长边为21cm,则其余两边之和为( )
A.24cm B.21cm C.13cm D.9cm
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
A. B. C. D.
如果两个相似三角形对应角平分线的比为16:25,那么它们的面积比为( )
A、4:5 B、16:25 C、196:225 D、256:625
二、填空题
已知△ABC∽△DEF,△ABC与△DEF的相似比为4:1,则△ABC与△DEF对应边上的高之比为______.
如图,已知△ABC∽△DEF,且相似比为k,则k=________,直线y=kx+k的图象必经过________象限.
已知△ABC∽△A′B′C′,∠A=50°,则∠A的对应角∠A′=________度.
两个三角形相似,其中一个三角形的两个内角是40°、60°.那么另一个三角形的最大角是________度,最小角是________度.
如图,矩形ABCD两邻边分别为3、4,点P是矩形一边上任意一点,则点P到两条对角线AC、BD的距离之和PE+PF为_____________.
矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间为_________________
三、解答题
两个相似三角形一组对应边的长分别是24cm和12cm,若他们周长的和是240cm,求这两个三角形的周长.
如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
如图,已知△ABC中,AB=8,BC=7,AC=6,点D、E分别在AB、AC上,如果以A、D、E为顶点的三角形和△ABC相似,且相似比为 ,试求AD、AE的长.
已知:如图,△ABC∽△ADE , AE:EC=5:3,BC=6cm,∠A=40°,∠C=45°.
(1)求∠ADE的大小;
(2)求DE的长.
如图,点D、E分别在△ABC的边AB、AC上,且AB=9,AC=6,AD=3,若使△ADE与△ABC相似,求AE的长.
(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
答案解析
一 、选择题
【考点】相似三角形的性质
【分析】设另一个三角形最短的一边是x,根据相似三角形对应边成比例即可得出结论.
解:设另一个三角形最短的一边是x,
∵△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,
∴,
解得x=18.
故选C.
【考点】相似三角形的性质
【分析】由△ABC与△DEF相似且面积比为4:1,根据相似三角形对应的面积比等于相似比的平方,即可求得△ABC与△DEF的相似比,又由相似三角形对应边上的高的比等于相似比即可求得答案.
解:∵△ABC与△DEF相似且面积比为4:1,
∴△ABC与△DEF的相似比为2:1,
∴△ABC与△DEF的对应边上的高之比2:1.
故选D.
【考点】相似三角形的性质
【分析】根据相似三角形面积的比等于相似比的平方,可求小三角形的面积为.
解:根据题意两个三角形的相似比是5:3,面积比就是25:9,
大小面积相差16份,所以每份的面积是32÷16=2(),所以小三角形的面积为2×9=18().
故选D.
【考点】相似三角形的性质
【分析】根据相似三角形对应边的比等于相似比即可求解.
解:∵△ABC∽△DEF,相似比为1:2,
∴,
∴EF=2BC=2.
故选:B.
【考点】相似三角形的性质
【分析】根据相似三角形面积的比等于相似比的平方计算即可得解.
解:∵△ABC∽△A′B′C′,相似比为1:2,
∴△ABC与△A′B′C′的面积的比为1:4.
故选:C.
【考点】相似三角形的性质
【分析】根据相似三角形对应边的比相等解答即可.
解:设其余两边的长分别是xcm,ycm,
由题意得x:y:21=3:5:7,
解得x=9,y=15,
故其余两边长的和为9+15=24(cm).
故选A.
【考点】相似三角形的性质AD
【分析】根据相似三角形的对应边成比例进行判断,要注意相似三角形的对应边和对应角.
解:∵△ABC∽△DBA,
∴;
∴,
;
故选AD.
【考点】相似三角形的性质
【分析】相似三角形对应角平分线的比等于相似比,面积比等于相似比的平方,即面积的比等于对应角平分线的比的平方.
解::根据两个相似三角形对应角平分线的比等于相似比,面积比等于相似比的平方,∴ ( http: / / www. / " \o "中国教育出版网\" )
它们的面积比为256:625.
故选:D.
二 、填空题
【考点】相似三角形的性质
【分析】根据相似三角形的对应边上的高之比等于相似比得出即可.
解:∵△ABC∽△DEF,△ABC与△DEF的相似比为4:1,
∴△ABC与△DEF对应边上的高之比是4:1,
故答案为:4:1.
【考点】相似三角形的性质
【分析】根据相似比的定义得出 =k , 推出c=(a+b)k , b=(a+c)k , a=(c+b)k , 求出k的值,即可求出答案.
解:k= = = ,
∴ =k ,
∴c=(a+b)k ,
b=(a+c)k ,
a=(c+b)k ,
相加得:(a+b+c)=2k(a+b+c),
当a+b+c=0时,k= = =-1,
∵相似比是k , ∴k=-1舍去;
当a+b+c≠0时,k= ,此时y= x+ 图象经过一、二、三象限;
故答案为: ,一、二、三.
【考点】相似三角形的性质
【分析】根据相似三角形的对应角相等解答.
解:∵△ABC∽△A′B′C′,∠A=50°,
∴∠A′=50度.
【考点】相似三角形的性质
【分析】由一个三角形的两个内角是40°、60°,根据三角形的内角各等于180°,求得第三个内角的度数,又由两个三角形相似,根据相似三角形的对应角相等,可求得答案.解答此题的关键是注意相似三角形的对应角相等.
解:∵一个三角形的两个内角是40°、60°.
∴另一个内角为:180°-40°-60°=80°,
∵两个三角形相似,
∴另一个三角形的最大角是80°,最小角是40°.
故答案为:80,40.
【考点】相似三角形的性质;矩形的性质
【分析】首先设未知线段为未知数,然后根据矩形的性质求出相似三角形,进而求解.
解:设PE=x,PF=a,PB=y.
∵∠PBF=∠ABD,∠PFB=∠DAB
∴△ABD∽△FBP,
∴,
同理可证,
∴a+x=×3=.
故答案为:.
【考点】相似三角形的性质,等腰三角形的性质,矩形的性质
【分析】由△PBE∽△DBC,可得∠PBE=∠DBC,继而可确定点P在BD上,然后再根据△APD是等腰三角形,分DP=DA、AP=DP两种情况进行讨论即可得.
解:∵四边形ABCD是矩形,∴∠BAD=∠C=90°,CD=AB=6,∴BD=10,
∵△PBE∽△DBC,
∴∠PBE=∠DBC,∴点P在BD上,
如图1,当DP=DA=8时,BP=2,
∵△PBE∽△DBC,
∴PE:CD=PB:DB=2:10,
∴PE:6=2:10,
∴PE=1.2;
如图2,当AP=DP时,此时P为BD中点,
∵△PBE∽△DBC,
∴PE:CD=PB:DB=1:2,
∴PE:6=1:2,
∴PE=3;
综上,PE的长为1.2或3,
故答案为:1.2或3.
【点睛】本题考查了相似三角形的性质,等腰三角形的性质,矩形的性质等,确定出点P在线段BD上是解题的关键.
15.【分析】首先设运动了ts,根据题意得:AP=2tcm,CQ=3tcm,然后分别从当△APQ∽△ABC与当△APQ∽△ACB时去分析求解即可求得答案.
解:设运动了ts,
根据题意得:AP=2tcm,CQ=3tcm,
则AQ=AC-CQ=16-3t(cm),
当△APQ∽△ABC时,,
即,
解得:t=;
当△APQ∽△ACB时,,
即,
解得:t=4;
故当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是:s或4s.
三 、解答题
【考点】相似三角形的性质
【分析】设两个三角形的周长分别为x、y,根据相似三角形周长的比等于对应边的比列出方程,然后求解即可.
解:设两个三角形的周长分别为x、y,
根据题意得,,
∴,
∵他们周长的和是240cm,
∴,
解得y=80,
x=2×80=160,
∴这两个三角形的周长分别为80cm和160cm.
【考点】相似三角形的性质
【分析】先根据勾股定理求出BE的长,再根据相似三角形的对应边成比例即可求出EF的长.
解:∵四边形ABCD是矩形,
∴∠BAE=90°,
∵AB=6,AE=9,
∴,
∵△ABE∽△DEF,
∴,即,
解得.
【考点】相似三角形的性质
【分析】利用三角形相似的性质分△ABC∽△ADE和△ABC∽△AED两种情况讨论即可求得AD、AE的长.
解:当△ABC∽△ADE时,相似比为 , = = ,
即: = = ,
解得:AD=2,AE=1.5;
当△ABC∽△AED时,
= = ,
即: = = ,
解得:AD=1.5,AE=2.
【考点】相似三角形的性质
【分析】先由三角形的内角和是180°求得∠ABC=95°;再由相似三角形的对应角相等得出∠ADE=∠ABC , 最后由等量代换求得∠ADE的大小;由AE:EC=5:3求得AE:AC=5:8,再根据相似三角形的对应边成比例求得DE的长度.此题主要考查了相似三角形的性质:相似三角形的对应角相等,对应边成比例.
(1)解:在△ABC中,∠A=40°,∠C=45°,
∴∠ABC=180°-40°-45°=95°;
又∵△ABC∽△ADE ,
∴∠ADE=∠ABC(相似三角形的对应角相等),
∴∠ADE =95°;
(2)解:∵AE:EC=5:3,
∴AE:AC=5:8;
又∵△ABC∽△ADE , BC=6cm,
∴ ,即
∴DE= cm.
【考点】相似三角形的性质
【分析】由于△ADE与△ABC相似,但其对应角不能确定,所以应分两种情况进行讨论.
解::①若∠AED对应∠B时,
= ,即 = ,
解得AE= ;
②当∠ADE对应∠B时,
= ,即 = ,
解得AE=2.
所以AE的长为2或 .
【考点】相似三角形的性质,等腰三角形的判定与性质,勾股定理,平行线的性质
【分析】(1)根据平行线的性质可得出∠ADB=∠OAC=75°,结合∠BOD=∠COA可得出△BOD∽△COA,利用相似三角形的性质可求出OD的值,进而可得出AD的值,由三角形内角和定理可得出∠ABD=75°=∠ADB,由等角对等边可得出AB=AD=4,此题得解;
(2)过点B作BE∥AD交AC于点E,同(1)可得出AE=4,在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解.
解:(1)∵BD∥AC,
∴∠ADB=∠OAC=75°.
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴==.
又∵AO=,
∴OD=AO=,
∴AD=AO+OD=4.
∵∠BAD=30°,∠ADB=75°,
∴∠ABD=180°﹣∠BAD﹣∠ADB=75°=∠ADB,
∴AB=AD=4.
故答案为:75;4.
(2)过点B作BE∥AD交AC于点E,如图所示.
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°.
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴==.
∵BO:OD=1:3,
∴==.
∵AO=3,
∴EO=,
∴AE=4.
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
∴AB=2BE.
在Rt△AEB中,BE2+AE2=AB2,即(4)2+BE2=(2BE)2,
解得:BE=4,
∴AB=AC=8,AD=12.
在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,
解得:CD=4.
【点评】本题考查了相似三角形的性质、等腰三角形的判定与性质、勾股定理以及平行线的性质,解题的关键是:(1)利用相似三角形的性质求出OD的值;(2)利用勾股定理求出BE、CD的长度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
