22.3 相似三角形的性质(2)同步作业
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
22.3 相似三角形的性质(2)同步作业
姓名:__________班级:__________考号:__________
一 、选择题
将直角三角形的三条边长同时扩大同一倍数,得到的三角形是( )
A、等腰三角形 B、锐角三角形 C、直角三角形 D、钝角三角形
如图,△ABC, AB=12,AC=15,D为AB上一点,且AD= AB , 在AC上取一点E, 使以A、D、E为顶点的三角形与ABC相似,则AE等于( )
A、 B、10 C、或10 D、以上答案都不对
如图,△ABC中,D、E分别为边AB、AC上的点,且DE∥BC,下列判断错误的是( )
A. HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 B. C. D.
等腰△ABC中,AB=AC,∠A=36°,D是AC上的一点,AD=BD,则以下结论中正确的有( )①△BCD是等腰三角形;②点D是线段AC的黄金分割点;③△BCD∽△ABC;④BD平分∠ABC.
A.1个 B.2个 C.3个 D.4个
如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=( )
A.16 B.18 C.20 D.24
如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.= B.= C.= D.=
如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
A. B. C. D.
如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
A. B. 2 C. D. 4
二、填空题
如图,已知AB∥CD,若=,则= .
已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 .
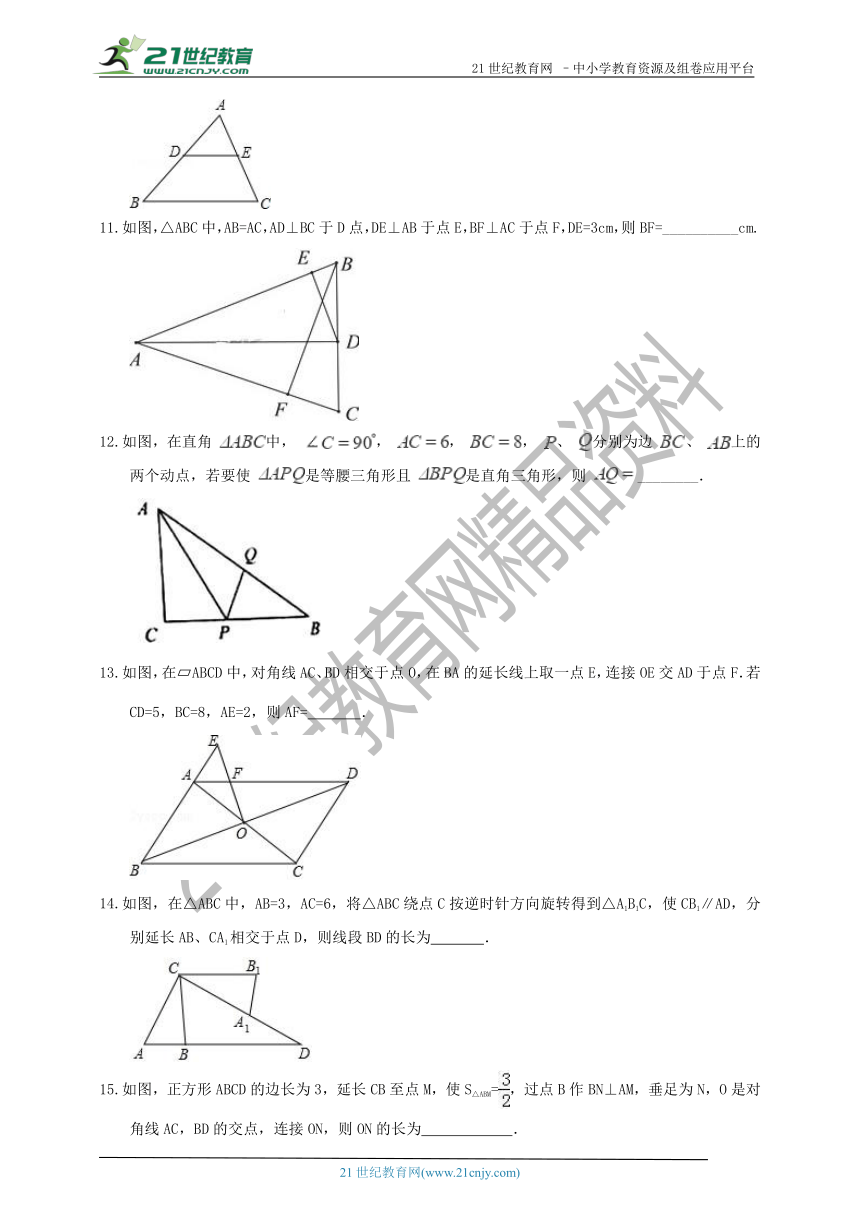
如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=__________cm.
如图,在直角 中, , , , 、 分别为边 、 上的两个动点,若要使 是等腰三角形且 是直角三角形,则 ________.
如图,在 ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF= .
如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为 .
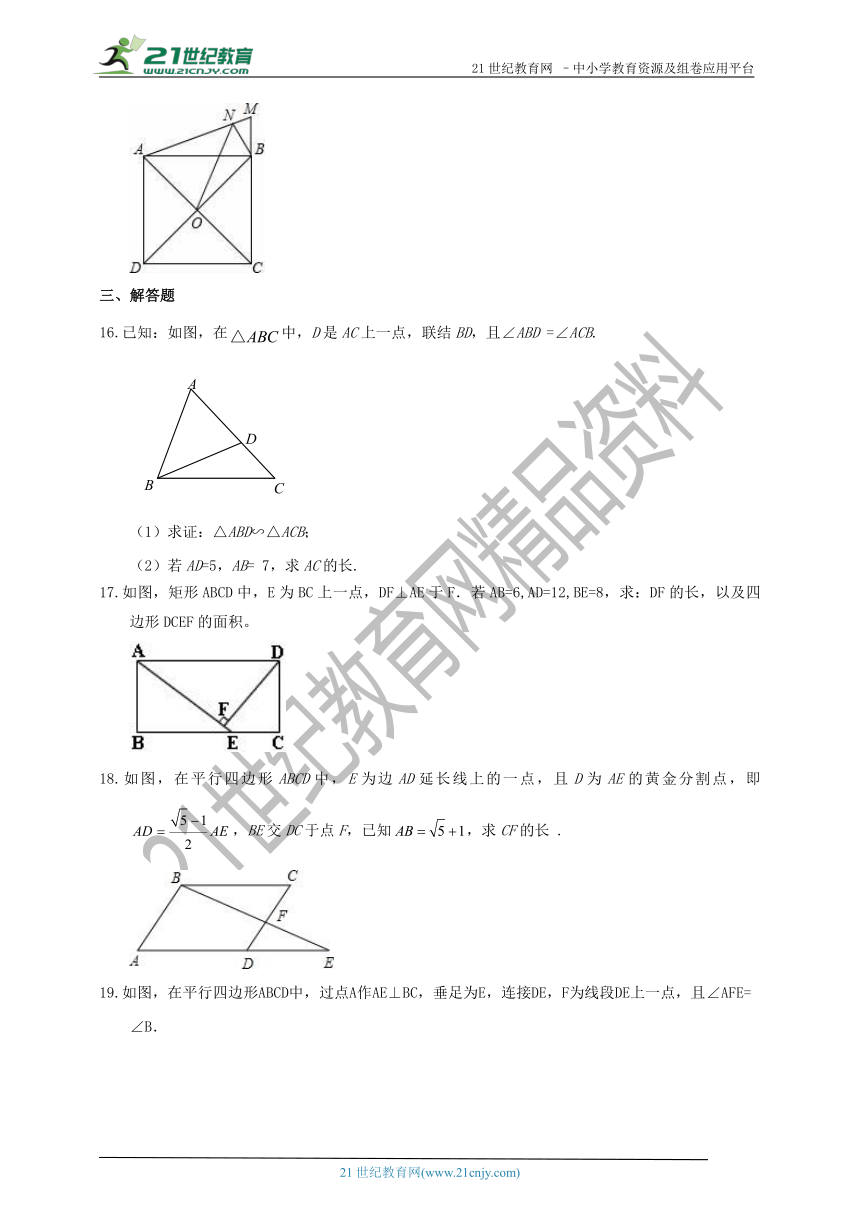
如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM=,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为 .
三、解答题
已知:如图,在中,D是AC上一点,联结BD,且∠ABD =∠ACB.
(1)求证:△ABD∽△ACB;
(2)若AD=5,AB= 7,求AC的长.
如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.若AB=6,AD=12,BE=8,求:DF的长,以及四边形DCEF的面积。
如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即,BE交DC于点F,已知,求CF的长 .
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
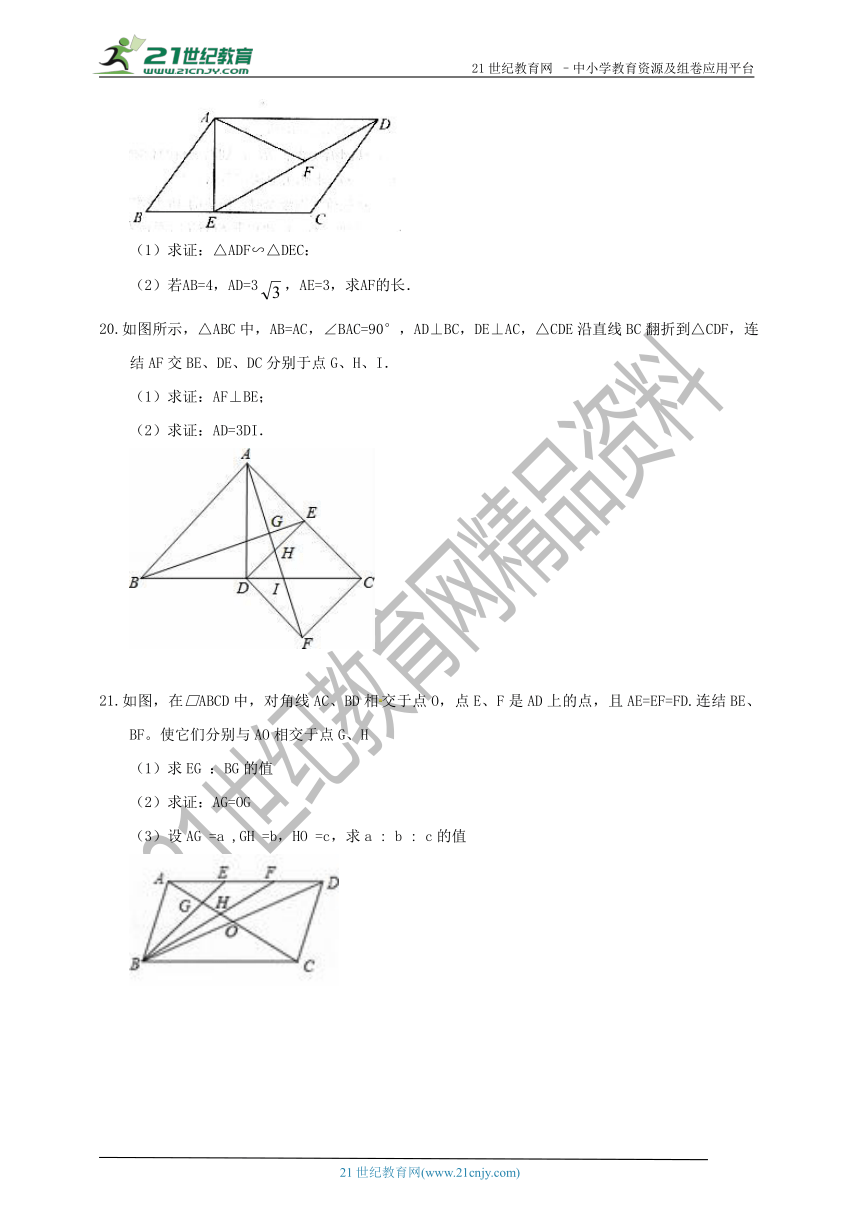
(1)求证:△ADF∽△DEC:
(2)若AB=4,AD=3,AE=3,求AF的长.
如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.
(1)求证:AF⊥BE;
(2)求证:AD=3DI.
如图,在□ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连结BE、BF。使它们分别与AO相交于点G、H
(1)求EG :BG的值
(2)求证:AG=OG
(3)设AG =a ,GH =b,HO =c,求a : b : c的值
答案解析
一 、选择题
【考点】相似三角形的判定与性质
【分析】根据三组对应边的比相等的三角形相似,再由相似三角形的性质即可求解.此题主要考查相似三角形的判定及性质.
解:将直角三角形的三条边长同时扩大同一倍数,得到的三角形与原三角形相似,根据相似三角形的对应角相等可知得到的三角形是直角三角形.故选:C.
【考点】相似三角形的判定与性质
【分析】若以A、D、E为顶点的三角形与△ABC相似,则存在两种情况,即△AED∽△ACB , △AED∽△ABC , 应分类讨论求解.
解::如图:
①当∠AED=∠C时,即DE∥BC
则AE = ( http: / / www. / " \o "中国教育出版网\" )AC=10
②当∠AED=∠B时,△AED∽△ABC
∴ ,即
AE=
综合①,②,故选:C.
【考点】相似三角形的判定与性质
【分析】如图,证明△ADE∽△ABC,得到;证明 HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,即可解决问题.
解:如图,∵DE∥BC,
( http: / / www. / " \o "中国教育出版网\" )
∴△ADE∽△ABC,
∴,
∴C、D正确.
∵DE∥BC,
∴,
故选B.
【考点】 黄金分割;等腰三角形的性质;相似三角形的判定与性质.
【分析】 先根据等腰三角形的性质和三角形内角和定理计算出∠ABC=∠C=
(180°-∠A)=72°,再计算出∠BDC=72°,∠DBC=36°,则可对①③④进行判断;利用△BCD∽△ABC得BD:AC=CD:BD,而AD=BD,则AD:AC=CD:AD,于是根据黄金分割的定义可对②进行判断.
解: ∵AB=AC,
∴∠ABC=∠C=(180°-∠A)= (180°-36°)=72°,
∵AD=BD,
∴∠DBA=∠A=36°,
∴∠BDC=2∠A=72°,
∴∠BDC=∠C,
∴△BCD为等腰三角形,所以①正确;
∴∠DBC=∠ABC-∠ABD=36°,
∴∠ABD=∠DBC,
∴BD平分∠ABC,所以④正确;
∵∠DBC=∠A,∠BCD=∠ACB,
∴△BCD∽△ABC,所以③正确;
∴BD:AC=CD:BD,
而AD=BD,
∴AD:AC=CD:AD,
∴点D是线段AC的黄金分割点,所以②正确.
【考点】相似三角形的判定和性质
【分析】由EF∥BC,可证明△AEF∽△ABC,利用相似三角形的性质即可求出则S△ABC的值.
解:∵EF∥BC,
∴△AEF∽△ABC,
∵AB=3AE,
∴AE:AB=1:3,
∴S△AEF:S△ABC=1:9,
设S△AEF=x,
∵S四边形BCFE=16,
∴=,
解得:x=2,
∴S△ABC=18,
故选:B.
【考点】相似三角形的判定与性质
【分析】由GE∥BD、GF∥AC可得出△AEG∽△ABD、△DFG∽△DCA,根据相似三角形的性质即可找出==,此题得解.
解:∵GE∥BD,GF∥AC,
∴△AEG∽△ABD,△DFG∽△DCA,
∴=,=,
∴==.
故选:D.
【点评】本题考查了相似三角形的判定与性质,利用相似三角形的性质找出==是解题的关键.
【考点】含30度角的直角三角形的性质,相似三角形的判定和性质,角平分线的定义
【分析】先利用含30度角的直角三角形的性质求出BD,再利用直角三角形的性质求出DE=BE=2,即:∠BDE=∠ABD,进而判断出DE∥AB,再求出AB=3,即可得出结论.
解:如图,
在Rt△BDC中,BC=4,∠DBC=30°,
∴BD=2,
连接DE,
∵∠BDC=90°,点D是BC中点,
∴DE=BE=CEBC=2,
∵∠DCB=30°,
∴∠BDE=∠DBC=30°,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠BDE,
∴DE∥AB,
∴△DEF∽△BAF,
∴,
在Rt△ABD中,∠ABD=30°,BD=2,
∴AB=3,
∴,
∴,
∴DF=BD=×2=,
故选:D.
【点评】此题主要考查了含30度角的直角三角形的性质,相似三角形的判定和性质,角平分线的定义,判断出DE∥是解本题的关键.
【考点】相似三角形的判定与性质,等边三角形的判定与性质,勾股定理,菱形的性质
【分析】根据菱形的性质得菱形边长为4,AC⊥BD,由一个角是60度的等腰三角形是等边三角形得△ABD是等边三角形;在Rt△AOD中,根据勾股定理得AO=2,AC=2AO=4,根据三角形面积公式得S△ACD=OD·AC=4,根据中位线定理得OE∥AD,根据相似三角形的面积比等于相似比继而可求出△OCE的面积.
解:∵菱形ABCD的周长为16,∴菱形ABCD的边长为4,
∵∠BAD=60°,
∴△ABD是等边三角形,
又∵O是菱形对角线AC、BD的交点,
∴AC⊥BD,
在Rt△AOD中,
∴AO=,
∴AC=2AO=4,
∴S△ACD=OD·AC= ×2×4=4,
又∵O、E分别是中点,
∴OE∥AD,
∴△COE∽△CAD,
∴,
∴,
∴S△COE=S△CAD=×4=,
故选A.
【点睛】本题考查了相似三角形的判定与性质,等边三角形的判定与性质,勾股定理,菱形的性质,结合图形熟练应用相关性质是解题的关键.
二、填空题
【考点】平行线的性质,相似三角形的判定和性质
【分析】利用相似三角形的性质即可解决问题;
解:∵AB∥CD,
∴△AOB∽△COD,
∴==,
故答案为.
【点评】本题考查平行线的性质,相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【考点】相似三角形的判定与性质
【分析】设四边形BCED的面积为x,则S△ADE=12﹣x,由题意知DE∥BC且DE=BC,从而得=()2,据此建立关于x的方程,解之可得.
解:设四边形BCED的面积为x,则S△ADE=12﹣x,
∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,且DE=BC,
∴△ADE∽△ABC,
则=()2,即=,
解得:x=9,
即四边形BCED的面积为9,
故答案为:9.
【点评】本题主要考查相似三角形的判定与性质,解题的关键是掌握中位线定理及相似三角形的面积比等于相似比的平方的性质.
【考点】等腰三角形的性质、相似三角形的判定与性质
【分析】由等腰三角形的性质可得∠C =∠ABC, BD=DC=BC,再根据∠BED=∠CFB=90°,可证△BED∽△CFB,根据相似三角形的对应边成比例即可求得.
解:∵AB=AC,
∴∠C =∠ABC ,
又∵AD ⊥BC于 D 点,
∴ BD=DC=BC,
又 DE ⊥AB,BF ⊥AC,
∴∠BED=∠CFB=90°,
∴△BED∽△CFB,
∴DE:BF=BD:BC=1:2,
∴BF=2DE=2×3=6cm ,
故答案为:6.
【点睛】本题考查了等腰三角形的性质、相似三角形的判定与性质,得到△BED∽△CFB是解本题的关键.
【考点】等腰三角形的判定与性质,相似三角形的判定与性质
【分析】要同时使 是等腰三角形且 是直角三角形,要先找突破口,可先确定当△APQ是等腰三角形时,再讨论△BPQ是直角三角形可能的情况;或者先确定△BPQ是直角三角形,再讨论△APQ是等腰三角形的情况;此题先确定△BPQ是直角三角形容易一些:△BPQ是直角三角形有两种情况,根据相似的判定和性质可得到△BQP与△BCA相似,可得到△BQP三边之比,设出未知数表示出三边的长度,再讨论△APQ是等腰三角形时,是哪两条相等,构造方程解出未知数即可,最后求出AQ。
解:当△BPQ是直角三角形时,有两种情况:∠BPQ=90度,∠BQP=90度。在直角 中, , , ,则AB=10,AC:BC:AB=3:4:5.( 1 )当∠BPQ=90度,则△BPQ~△BCA,则PQ:BP:BQ=AC:BC:AB=3:4:5,
设PQ=3x,则BP=4x,BQ=5x,AQ=AB-BQ=10-5x,
此时∠AQP为钝角,则当△APQ是等腰三角形时,只有AQ=PQ,
则10-5x=3x,解得x= ,
则AQ=10-5x= ;
( 2 )当∠BQP =90度,则△BQP~△BCA,则PQ:BQ:BP=AC:BC:AB=3:4:5,
设PQ=3x,则BQ=4x,BP=5x,AQ=AB-BQ=10-4x,
此时∠AQP为直角,则当△APQ是等腰三角形时,只有AQ=PQ,
则10-4x=3x,解得x= ,
则AQ=10-4x= ;
故答案为: 或
【考点】相似三角形的判定与性质;平行四边形的性质.
【分析】过O点作OM∥AD,求出AM和MO的长,利用△AEF∽△MEO,得到关于AF的比例式,求出AF的长即可.
解:过O点作OM∥AD,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OM是△ABD的中位线,
∴AM=BM=AB=,OM=BC=4,
∵AF∥OM,
∴△AEF∽△MEO,
∴=,
∴=,
∴AF=,
故答案为.
【考点】旋转的性质;平行线的判定.相似三角形的判定与性质
【分析】利用平行线的性质以及旋转的性质得出△CAD∽△B1A1C,再利用相似三角形的性质得出AD的长,进而得出BD的长.
解:∵将△ABC绕点C按逆时针方向旋转得到△A1B1C,
∴AC=CA1=6,AB=B1A1=3,∠A=∠CA1B1,
∵CB1∥AB,
∴∠B1CA1=∠D,
∴△CAD∽△B1A1C,
∴,
∴,
解得AD=12,
∴BD=AD﹣AB=12﹣3=9.
故答案为:9.
【考点】相似三角形的判定与性质;正方形的性质.
【分析】先根据三角形的面积公式求出BM的长,由条件可证得△ABN∽△BNM∽△ABM,且可求得AM=,利用对应线段的比相等可求得AN和MN,进一步可得到=,且∠CAM=∠NAO,可证得△AON∽△AMC,利用相似三角形的性质可求得ON
【解答】解:∵正方形ABCD的边长为3,S△ABM=,
∴BM=.
∵AB=3,BM=1,
∴AM=,
∵∠ABM=90°,BN⊥AM,
∴△ABN∽△BNM∽△AMB,
∴AB2=AN×AM,BM2=MN×AM,
∴AN=,MN=,
∵AB=3,CD=3,
∴AC=3,
∴AO=,
∵=, =,
∴=,且∠CAM=∠NAO
∴△AON∽△AMC,
∴==,
∴ON=.
故答案为:.
【点评】本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.
三 、解答题
16.【分析】(1)由∠A=∠A,∠ABD=∠ACB,根据有两角对应相等的三角形相似,即可证得:△ABD∽△ACB;
(2)由相似三角形的对应边成比例,即可求得AC的长
解:(1)∵∠ABD=∠C,∠A=∠A
∴△ABD∽△ACB
(2).∵△ABD∽△ACB
∴
即
∴AC=
【考点】矩形的性质,勾股定理,相似三角形是判定与性质,矩形与三角形的面积
【分析】先利用勾股定理,求出AE的长,再利用已知条件求出△AFD∽△EBA,得==,然后将已知数值代入即可求出DF的长.最后利用=SABCD-S△ABE- S△ADF计算出面积
解:在矩形中,∠B=90°,AB=6,BE=8,
∴AE=10
∵,AD∥BC
∴∠B=∠DFA=90°, ∠DAF=∠AEB
∴△AFD∽△EBA
∴,
∴DF=7.2
∴AF=9.6
=6×12-×6×8-×9.6×7.2=13.44
【分析】根据平行四边形的性质得出∠CBF=∠AEB,∠BCF=∠BAE,从而得出△BCF∽△EAB,根据相似三角形比例关系即可得出答案.
解:∵D为AE的黄金分割点,
∴AD=
∵四边形ABCD为平行四边形,
∴∠CBF=∠AEB,∠BCF=∠BAE,BC=AD,
∴△BCF∽△EAB,
∴,即 ,
把AD=,AB=+1代入得,=,
解得:CF=2.
19.【分析】(1)△ADF和△DEC中,易知∠ADF=∠CED(平行线的内错角),而∠AFD和∠C是等角的补角,由此可判定两个三角形相似;
(2)在Rt△ABE中,由勾股定理易求得DE的长,再根据相似三角形的对应边成比例即可求出AF的长.
(1)证明:∵四边形ABCD是平行四边形
∴AD∥BC, AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°.
∵∠AFE+∠AFD=180,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC CD=AB=4.
又∵AE⊥BC ,∴ AE⊥AD.
在Rt△ADE中,DE=.
∵△ADF∽△DEC,∴.∴.AF=.
【考点】翻折变换(折叠问题);全等三角形的判定与性质;平行线分线段成比例.
【分析】(1)根据翻折的性质和SAS证明△ABE与△ACF全等,利用全等三角形的性质得出∠AGB=90°证明即可;
(2)作IC的中点M,利用AAS证明△AEH与△FDH全等,再利用全等三角形的性质和中位线的性质解答即可.
证明:(1)∵在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,
∴AD=BD=CD,∠ACB=45°,
∵在△ADC中,AD=DC,DE⊥AC,
∴AE=CE,
∵△CDE沿直线BC翻折到△CDF,
∴△CDE≌△CDF,
∴CF=CE,∠DCF=∠ACB=45°,
∴CF=AE,∠ACF=∠DCF+∠ACB=90°,
在△ABE与△ACF中,,
∴△ABE≌△ACF(SAS),
∴∠ABE=∠FAC,
∵∠BAG+∠CAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE;
(2)作IC的中点M,连接EM,由(1)∠DEC=∠ECF=∠CFD=90°
∴四边形DECF是正方形,
∴EC∥DF,EC=DF,
∴∠EAH=∠HFD,AE=DF,
在△AEH与△FDH中,
∴△AEH≌△FDH(AAS),
∴EH=DH,
∵∠BAG+∠CAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE,
∵M是IC的中点,E是AC的中点,
∴EM∥AI,
∴,
∴DI=IM,
∴CD=DI+IM+MC=3DI,
∴AD=3DI.
【点评】此题考查翻折问题,关键是利用SAS和AAS证明三角形全等,再利用全等三角形的性质进行分析解答.
【分析】(1)根据平行四边形的性质可得AO=AC,AD=BC,AD∥BC,从而可得△AEG∽△CBG,由AE=EF=FD可得BC=3AE,然后根据相似三角形的性质,即可求出EG:BG的值;
(2)根据相似三角形的性质可得GC=3AG,则有AC=4AG,从而可得AO=AC=2AG,即可得到GO=AO﹣AG=AG;
(3)根据相似三角形的性质可得AG=AC,AH=AC,结合AO=AC,即可得到a=AC,b=AC,c=AC,就可得到a:b:c的值.
解:(1)∵四边形ABCD是平行四边形,
∴AO= ( http: / / www. / " \o "中国教育出版网\" )AC,AD=BC,AD∥BC,
∴△AEG∽△CBG,
∴==.
∵AE=EF=FD,
∴BC=AD=3AE,
∴GC=3AG,GB=3EG,
∴EG:BG=1:3;
(2)∵GC=3AG(已证),
∴AC=4AG,
∴AO= ( http: / / www. / " \o "中国教育出版网\" )AC=2AG,
∴GO=AO﹣AG=AG;
(3)∵AE=EF=FD,
∴BC=AD=3AE,AF=2AE.
∵AD∥BC,
∴△AFH∽△CBH,
∴=== ( http: / / www. / " \o "中国教育出版网\" ),
∴=,即AH=AC.
∵AC=4AG,
∴a=AG= ( http: / / www. / " \o "中国教育出版网\" )AC,
b=AH﹣AG=AC﹣AC=AC,
c=AO﹣AH= ( http: / / www. / " \o "中国教育出版网\" )AC﹣AC=AC,
∴a:b:c=: ( http: / / www. / " \o "中国教育出版网\" ):=5:3:2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
22.3 相似三角形的性质(2)同步作业
姓名:__________班级:__________考号:__________
一 、选择题
将直角三角形的三条边长同时扩大同一倍数,得到的三角形是( )
A、等腰三角形 B、锐角三角形 C、直角三角形 D、钝角三角形
如图,△ABC, AB=12,AC=15,D为AB上一点,且AD= AB , 在AC上取一点E, 使以A、D、E为顶点的三角形与ABC相似,则AE等于( )
A、 B、10 C、或10 D、以上答案都不对
如图,△ABC中,D、E分别为边AB、AC上的点,且DE∥BC,下列判断错误的是( )
A. HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 B. C. D.
等腰△ABC中,AB=AC,∠A=36°,D是AC上的一点,AD=BD,则以下结论中正确的有( )①△BCD是等腰三角形;②点D是线段AC的黄金分割点;③△BCD∽△ABC;④BD平分∠ABC.
A.1个 B.2个 C.3个 D.4个
如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=( )
A.16 B.18 C.20 D.24
如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.= B.= C.= D.=
如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
A. B. C. D.
如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
A. B. 2 C. D. 4
二、填空题
如图,已知AB∥CD,若=,则= .
已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 .
如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=__________cm.
如图,在直角 中, , , , 、 分别为边 、 上的两个动点,若要使 是等腰三角形且 是直角三角形,则 ________.
如图,在 ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF= .
如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为 .
如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM=,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为 .
三、解答题
已知:如图,在中,D是AC上一点,联结BD,且∠ABD =∠ACB.
(1)求证:△ABD∽△ACB;
(2)若AD=5,AB= 7,求AC的长.
如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.若AB=6,AD=12,BE=8,求:DF的长,以及四边形DCEF的面积。
如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即,BE交DC于点F,已知,求CF的长 .
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC:
(2)若AB=4,AD=3,AE=3,求AF的长.
如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.
(1)求证:AF⊥BE;
(2)求证:AD=3DI.
如图,在□ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连结BE、BF。使它们分别与AO相交于点G、H
(1)求EG :BG的值
(2)求证:AG=OG
(3)设AG =a ,GH =b,HO =c,求a : b : c的值
答案解析
一 、选择题
【考点】相似三角形的判定与性质
【分析】根据三组对应边的比相等的三角形相似,再由相似三角形的性质即可求解.此题主要考查相似三角形的判定及性质.
解:将直角三角形的三条边长同时扩大同一倍数,得到的三角形与原三角形相似,根据相似三角形的对应角相等可知得到的三角形是直角三角形.故选:C.
【考点】相似三角形的判定与性质
【分析】若以A、D、E为顶点的三角形与△ABC相似,则存在两种情况,即△AED∽△ACB , △AED∽△ABC , 应分类讨论求解.
解::如图:
①当∠AED=∠C时,即DE∥BC
则AE = ( http: / / www. / " \o "中国教育出版网\" )AC=10
②当∠AED=∠B时,△AED∽△ABC
∴ ,即
AE=
综合①,②,故选:C.
【考点】相似三角形的判定与性质
【分析】如图,证明△ADE∽△ABC,得到;证明 HYPERLINK "http://www./" \o "中国教育出版网\" " EMBED Equation.DSMT4 ,即可解决问题.
解:如图,∵DE∥BC,
( http: / / www. / " \o "中国教育出版网\" )
∴△ADE∽△ABC,
∴,
∴C、D正确.
∵DE∥BC,
∴,
故选B.
【考点】 黄金分割;等腰三角形的性质;相似三角形的判定与性质.
【分析】 先根据等腰三角形的性质和三角形内角和定理计算出∠ABC=∠C=
(180°-∠A)=72°,再计算出∠BDC=72°,∠DBC=36°,则可对①③④进行判断;利用△BCD∽△ABC得BD:AC=CD:BD,而AD=BD,则AD:AC=CD:AD,于是根据黄金分割的定义可对②进行判断.
解: ∵AB=AC,
∴∠ABC=∠C=(180°-∠A)= (180°-36°)=72°,
∵AD=BD,
∴∠DBA=∠A=36°,
∴∠BDC=2∠A=72°,
∴∠BDC=∠C,
∴△BCD为等腰三角形,所以①正确;
∴∠DBC=∠ABC-∠ABD=36°,
∴∠ABD=∠DBC,
∴BD平分∠ABC,所以④正确;
∵∠DBC=∠A,∠BCD=∠ACB,
∴△BCD∽△ABC,所以③正确;
∴BD:AC=CD:BD,
而AD=BD,
∴AD:AC=CD:AD,
∴点D是线段AC的黄金分割点,所以②正确.
【考点】相似三角形的判定和性质
【分析】由EF∥BC,可证明△AEF∽△ABC,利用相似三角形的性质即可求出则S△ABC的值.
解:∵EF∥BC,
∴△AEF∽△ABC,
∵AB=3AE,
∴AE:AB=1:3,
∴S△AEF:S△ABC=1:9,
设S△AEF=x,
∵S四边形BCFE=16,
∴=,
解得:x=2,
∴S△ABC=18,
故选:B.
【考点】相似三角形的判定与性质
【分析】由GE∥BD、GF∥AC可得出△AEG∽△ABD、△DFG∽△DCA,根据相似三角形的性质即可找出==,此题得解.
解:∵GE∥BD,GF∥AC,
∴△AEG∽△ABD,△DFG∽△DCA,
∴=,=,
∴==.
故选:D.
【点评】本题考查了相似三角形的判定与性质,利用相似三角形的性质找出==是解题的关键.
【考点】含30度角的直角三角形的性质,相似三角形的判定和性质,角平分线的定义
【分析】先利用含30度角的直角三角形的性质求出BD,再利用直角三角形的性质求出DE=BE=2,即:∠BDE=∠ABD,进而判断出DE∥AB,再求出AB=3,即可得出结论.
解:如图,
在Rt△BDC中,BC=4,∠DBC=30°,
∴BD=2,
连接DE,
∵∠BDC=90°,点D是BC中点,
∴DE=BE=CEBC=2,
∵∠DCB=30°,
∴∠BDE=∠DBC=30°,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠BDE,
∴DE∥AB,
∴△DEF∽△BAF,
∴,
在Rt△ABD中,∠ABD=30°,BD=2,
∴AB=3,
∴,
∴,
∴DF=BD=×2=,
故选:D.
【点评】此题主要考查了含30度角的直角三角形的性质,相似三角形的判定和性质,角平分线的定义,判断出DE∥是解本题的关键.
【考点】相似三角形的判定与性质,等边三角形的判定与性质,勾股定理,菱形的性质
【分析】根据菱形的性质得菱形边长为4,AC⊥BD,由一个角是60度的等腰三角形是等边三角形得△ABD是等边三角形;在Rt△AOD中,根据勾股定理得AO=2,AC=2AO=4,根据三角形面积公式得S△ACD=OD·AC=4,根据中位线定理得OE∥AD,根据相似三角形的面积比等于相似比继而可求出△OCE的面积.
解:∵菱形ABCD的周长为16,∴菱形ABCD的边长为4,
∵∠BAD=60°,
∴△ABD是等边三角形,
又∵O是菱形对角线AC、BD的交点,
∴AC⊥BD,
在Rt△AOD中,
∴AO=,
∴AC=2AO=4,
∴S△ACD=OD·AC= ×2×4=4,
又∵O、E分别是中点,
∴OE∥AD,
∴△COE∽△CAD,
∴,
∴,
∴S△COE=S△CAD=×4=,
故选A.
【点睛】本题考查了相似三角形的判定与性质,等边三角形的判定与性质,勾股定理,菱形的性质,结合图形熟练应用相关性质是解题的关键.
二、填空题
【考点】平行线的性质,相似三角形的判定和性质
【分析】利用相似三角形的性质即可解决问题;
解:∵AB∥CD,
∴△AOB∽△COD,
∴==,
故答案为.
【点评】本题考查平行线的性质,相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【考点】相似三角形的判定与性质
【分析】设四边形BCED的面积为x,则S△ADE=12﹣x,由题意知DE∥BC且DE=BC,从而得=()2,据此建立关于x的方程,解之可得.
解:设四边形BCED的面积为x,则S△ADE=12﹣x,
∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,且DE=BC,
∴△ADE∽△ABC,
则=()2,即=,
解得:x=9,
即四边形BCED的面积为9,
故答案为:9.
【点评】本题主要考查相似三角形的判定与性质,解题的关键是掌握中位线定理及相似三角形的面积比等于相似比的平方的性质.
【考点】等腰三角形的性质、相似三角形的判定与性质
【分析】由等腰三角形的性质可得∠C =∠ABC, BD=DC=BC,再根据∠BED=∠CFB=90°,可证△BED∽△CFB,根据相似三角形的对应边成比例即可求得.
解:∵AB=AC,
∴∠C =∠ABC ,
又∵AD ⊥BC于 D 点,
∴ BD=DC=BC,
又 DE ⊥AB,BF ⊥AC,
∴∠BED=∠CFB=90°,
∴△BED∽△CFB,
∴DE:BF=BD:BC=1:2,
∴BF=2DE=2×3=6cm ,
故答案为:6.
【点睛】本题考查了等腰三角形的性质、相似三角形的判定与性质,得到△BED∽△CFB是解本题的关键.
【考点】等腰三角形的判定与性质,相似三角形的判定与性质
【分析】要同时使 是等腰三角形且 是直角三角形,要先找突破口,可先确定当△APQ是等腰三角形时,再讨论△BPQ是直角三角形可能的情况;或者先确定△BPQ是直角三角形,再讨论△APQ是等腰三角形的情况;此题先确定△BPQ是直角三角形容易一些:△BPQ是直角三角形有两种情况,根据相似的判定和性质可得到△BQP与△BCA相似,可得到△BQP三边之比,设出未知数表示出三边的长度,再讨论△APQ是等腰三角形时,是哪两条相等,构造方程解出未知数即可,最后求出AQ。
解:当△BPQ是直角三角形时,有两种情况:∠BPQ=90度,∠BQP=90度。在直角 中, , , ,则AB=10,AC:BC:AB=3:4:5.( 1 )当∠BPQ=90度,则△BPQ~△BCA,则PQ:BP:BQ=AC:BC:AB=3:4:5,
设PQ=3x,则BP=4x,BQ=5x,AQ=AB-BQ=10-5x,
此时∠AQP为钝角,则当△APQ是等腰三角形时,只有AQ=PQ,
则10-5x=3x,解得x= ,
则AQ=10-5x= ;
( 2 )当∠BQP =90度,则△BQP~△BCA,则PQ:BQ:BP=AC:BC:AB=3:4:5,
设PQ=3x,则BQ=4x,BP=5x,AQ=AB-BQ=10-4x,
此时∠AQP为直角,则当△APQ是等腰三角形时,只有AQ=PQ,
则10-4x=3x,解得x= ,
则AQ=10-4x= ;
故答案为: 或
【考点】相似三角形的判定与性质;平行四边形的性质.
【分析】过O点作OM∥AD,求出AM和MO的长,利用△AEF∽△MEO,得到关于AF的比例式,求出AF的长即可.
解:过O点作OM∥AD,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OM是△ABD的中位线,
∴AM=BM=AB=,OM=BC=4,
∵AF∥OM,
∴△AEF∽△MEO,
∴=,
∴=,
∴AF=,
故答案为.
【考点】旋转的性质;平行线的判定.相似三角形的判定与性质
【分析】利用平行线的性质以及旋转的性质得出△CAD∽△B1A1C,再利用相似三角形的性质得出AD的长,进而得出BD的长.
解:∵将△ABC绕点C按逆时针方向旋转得到△A1B1C,
∴AC=CA1=6,AB=B1A1=3,∠A=∠CA1B1,
∵CB1∥AB,
∴∠B1CA1=∠D,
∴△CAD∽△B1A1C,
∴,
∴,
解得AD=12,
∴BD=AD﹣AB=12﹣3=9.
故答案为:9.
【考点】相似三角形的判定与性质;正方形的性质.
【分析】先根据三角形的面积公式求出BM的长,由条件可证得△ABN∽△BNM∽△ABM,且可求得AM=,利用对应线段的比相等可求得AN和MN,进一步可得到=,且∠CAM=∠NAO,可证得△AON∽△AMC,利用相似三角形的性质可求得ON
【解答】解:∵正方形ABCD的边长为3,S△ABM=,
∴BM=.
∵AB=3,BM=1,
∴AM=,
∵∠ABM=90°,BN⊥AM,
∴△ABN∽△BNM∽△AMB,
∴AB2=AN×AM,BM2=MN×AM,
∴AN=,MN=,
∵AB=3,CD=3,
∴AC=3,
∴AO=,
∵=, =,
∴=,且∠CAM=∠NAO
∴△AON∽△AMC,
∴==,
∴ON=.
故答案为:.
【点评】本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.
三 、解答题
16.【分析】(1)由∠A=∠A,∠ABD=∠ACB,根据有两角对应相等的三角形相似,即可证得:△ABD∽△ACB;
(2)由相似三角形的对应边成比例,即可求得AC的长
解:(1)∵∠ABD=∠C,∠A=∠A
∴△ABD∽△ACB
(2).∵△ABD∽△ACB
∴
即
∴AC=
【考点】矩形的性质,勾股定理,相似三角形是判定与性质,矩形与三角形的面积
【分析】先利用勾股定理,求出AE的长,再利用已知条件求出△AFD∽△EBA,得==,然后将已知数值代入即可求出DF的长.最后利用=SABCD-S△ABE- S△ADF计算出面积
解:在矩形中,∠B=90°,AB=6,BE=8,
∴AE=10
∵,AD∥BC
∴∠B=∠DFA=90°, ∠DAF=∠AEB
∴△AFD∽△EBA
∴,
∴DF=7.2
∴AF=9.6
=6×12-×6×8-×9.6×7.2=13.44
【分析】根据平行四边形的性质得出∠CBF=∠AEB,∠BCF=∠BAE,从而得出△BCF∽△EAB,根据相似三角形比例关系即可得出答案.
解:∵D为AE的黄金分割点,
∴AD=
∵四边形ABCD为平行四边形,
∴∠CBF=∠AEB,∠BCF=∠BAE,BC=AD,
∴△BCF∽△EAB,
∴,即 ,
把AD=,AB=+1代入得,=,
解得:CF=2.
19.【分析】(1)△ADF和△DEC中,易知∠ADF=∠CED(平行线的内错角),而∠AFD和∠C是等角的补角,由此可判定两个三角形相似;
(2)在Rt△ABE中,由勾股定理易求得DE的长,再根据相似三角形的对应边成比例即可求出AF的长.
(1)证明:∵四边形ABCD是平行四边形
∴AD∥BC, AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°.
∵∠AFE+∠AFD=180,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC CD=AB=4.
又∵AE⊥BC ,∴ AE⊥AD.
在Rt△ADE中,DE=.
∵△ADF∽△DEC,∴.∴.AF=.
【考点】翻折变换(折叠问题);全等三角形的判定与性质;平行线分线段成比例.
【分析】(1)根据翻折的性质和SAS证明△ABE与△ACF全等,利用全等三角形的性质得出∠AGB=90°证明即可;
(2)作IC的中点M,利用AAS证明△AEH与△FDH全等,再利用全等三角形的性质和中位线的性质解答即可.
证明:(1)∵在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,
∴AD=BD=CD,∠ACB=45°,
∵在△ADC中,AD=DC,DE⊥AC,
∴AE=CE,
∵△CDE沿直线BC翻折到△CDF,
∴△CDE≌△CDF,
∴CF=CE,∠DCF=∠ACB=45°,
∴CF=AE,∠ACF=∠DCF+∠ACB=90°,
在△ABE与△ACF中,,
∴△ABE≌△ACF(SAS),
∴∠ABE=∠FAC,
∵∠BAG+∠CAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE;
(2)作IC的中点M,连接EM,由(1)∠DEC=∠ECF=∠CFD=90°
∴四边形DECF是正方形,
∴EC∥DF,EC=DF,
∴∠EAH=∠HFD,AE=DF,
在△AEH与△FDH中,
∴△AEH≌△FDH(AAS),
∴EH=DH,
∵∠BAG+∠CAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE,
∵M是IC的中点,E是AC的中点,
∴EM∥AI,
∴,
∴DI=IM,
∴CD=DI+IM+MC=3DI,
∴AD=3DI.
【点评】此题考查翻折问题,关键是利用SAS和AAS证明三角形全等,再利用全等三角形的性质进行分析解答.
【分析】(1)根据平行四边形的性质可得AO=AC,AD=BC,AD∥BC,从而可得△AEG∽△CBG,由AE=EF=FD可得BC=3AE,然后根据相似三角形的性质,即可求出EG:BG的值;
(2)根据相似三角形的性质可得GC=3AG,则有AC=4AG,从而可得AO=AC=2AG,即可得到GO=AO﹣AG=AG;
(3)根据相似三角形的性质可得AG=AC,AH=AC,结合AO=AC,即可得到a=AC,b=AC,c=AC,就可得到a:b:c的值.
解:(1)∵四边形ABCD是平行四边形,
∴AO= ( http: / / www. / " \o "中国教育出版网\" )AC,AD=BC,AD∥BC,
∴△AEG∽△CBG,
∴==.
∵AE=EF=FD,
∴BC=AD=3AE,
∴GC=3AG,GB=3EG,
∴EG:BG=1:3;
(2)∵GC=3AG(已证),
∴AC=4AG,
∴AO= ( http: / / www. / " \o "中国教育出版网\" )AC=2AG,
∴GO=AO﹣AG=AG;
(3)∵AE=EF=FD,
∴BC=AD=3AE,AF=2AE.
∵AD∥BC,
∴△AFH∽△CBH,
∴=== ( http: / / www. / " \o "中国教育出版网\" ),
∴=,即AH=AC.
∵AC=4AG,
∴a=AG= ( http: / / www. / " \o "中国教育出版网\" )AC,
b=AH﹣AG=AC﹣AC=AC,
c=AO﹣AH= ( http: / / www. / " \o "中国教育出版网\" )AC﹣AC=AC,
∴a:b:c=: ( http: / / www. / " \o "中国教育出版网\" ):=5:3:2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
