22.4 图形的位似变换同步作业
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
22.4 图形的位似变换同步作业
姓名:__________班级:__________考号:__________
一 、选择题
已知△ABC与△A1B1C1位似,△ABC与△A2B2C2位似,则( )
A. △A1B1C1与△A2B2C2全等
B. △A1B1C1与△A2B2C2位似
C. △A1B1C1与△A2B2C2相似但不一定位似
D. △A1B1C1与△A2B2C2不相似
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. B. C. D.
如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到新的线段,则点A的对应点坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
下列命题中真命题是( )
A.=()2一定成立 B.位似图形不可能全等
C.正多边形都是轴对称图形 D.圆锥的主视图一定是等边三角形
在平面直角坐标系中,点是线段上一点,以原点为位似中心把放大到原来的两倍,则点的对应点的坐标为( )
A. B. 或
C. D. 或
在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )
A.(5,1) B.(4,3) C.(3,4) D.(1,5)
如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(﹣1,2),则点P的坐标为( )
A. (﹣4,0) B. (﹣3,0) C. (﹣2,0) D. (﹣1.5,0)
如图,△ABC 经过位似变换得到△DEF,点 O 是位似中心且 OA=AD,则△ABC 与△DEF 的面 积比是( )
A.1:6 B.1:5 C.1:4 D.1:2
二、填空题
△OAB三个顶点的坐标分别为O(0,0),A(4,6),B(3,0),以O为位似中心,将△OAB缩小为原来的,得到△OA′B′,则点A的对应点A′的坐标为 .
已知在平面直角坐标系中,点A(﹣3,﹣1)、B(﹣2,﹣4)、C(﹣6,﹣5),以原点为位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为 .
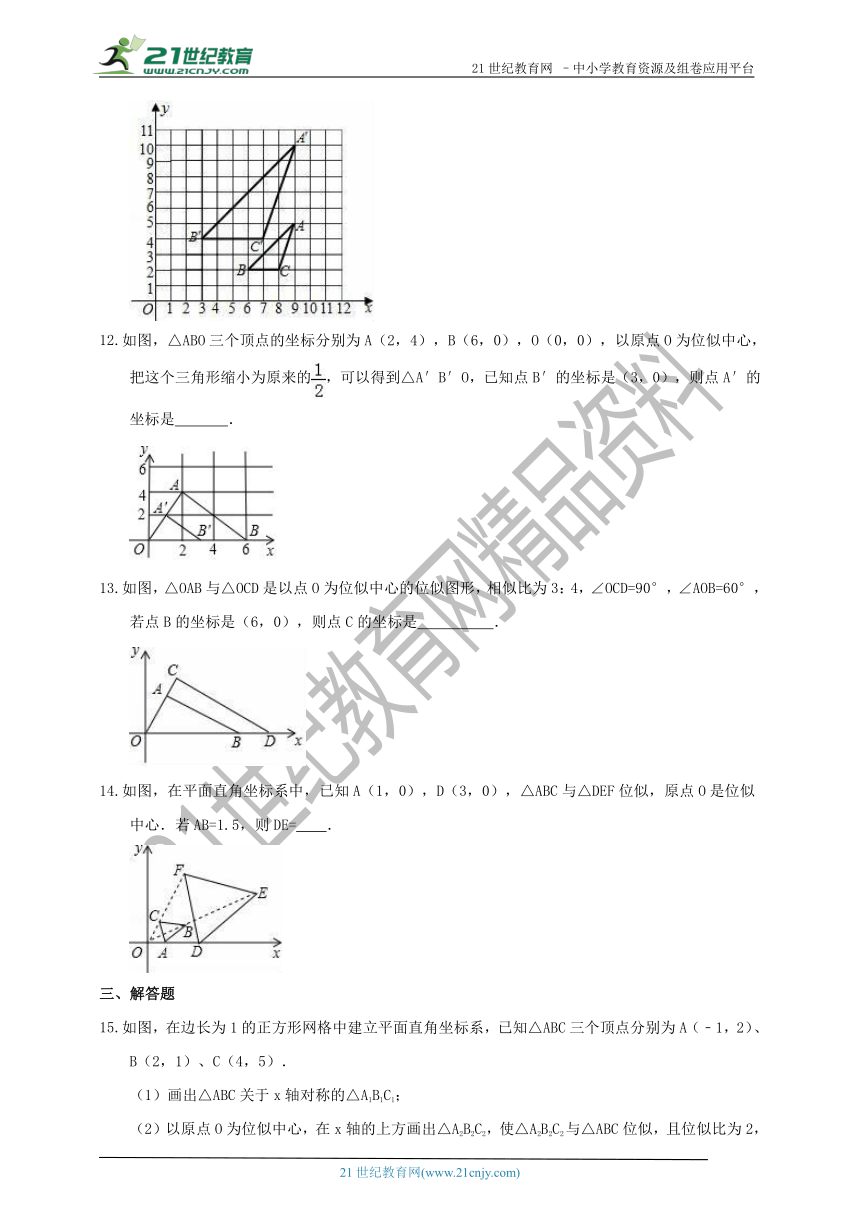
如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是 .
如图,△ABO三个顶点的坐标分别为A(2,4),B(6,0),O(0,0),以原点O为位似中心,把这个三角形缩小为原来的,可以得到△A′B′O,已知点B′的坐标是(3,0),则点A′的坐标是 .
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是 .
( http: / / www. / " \o "中国教育出版网\" )
如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .
三、解答题
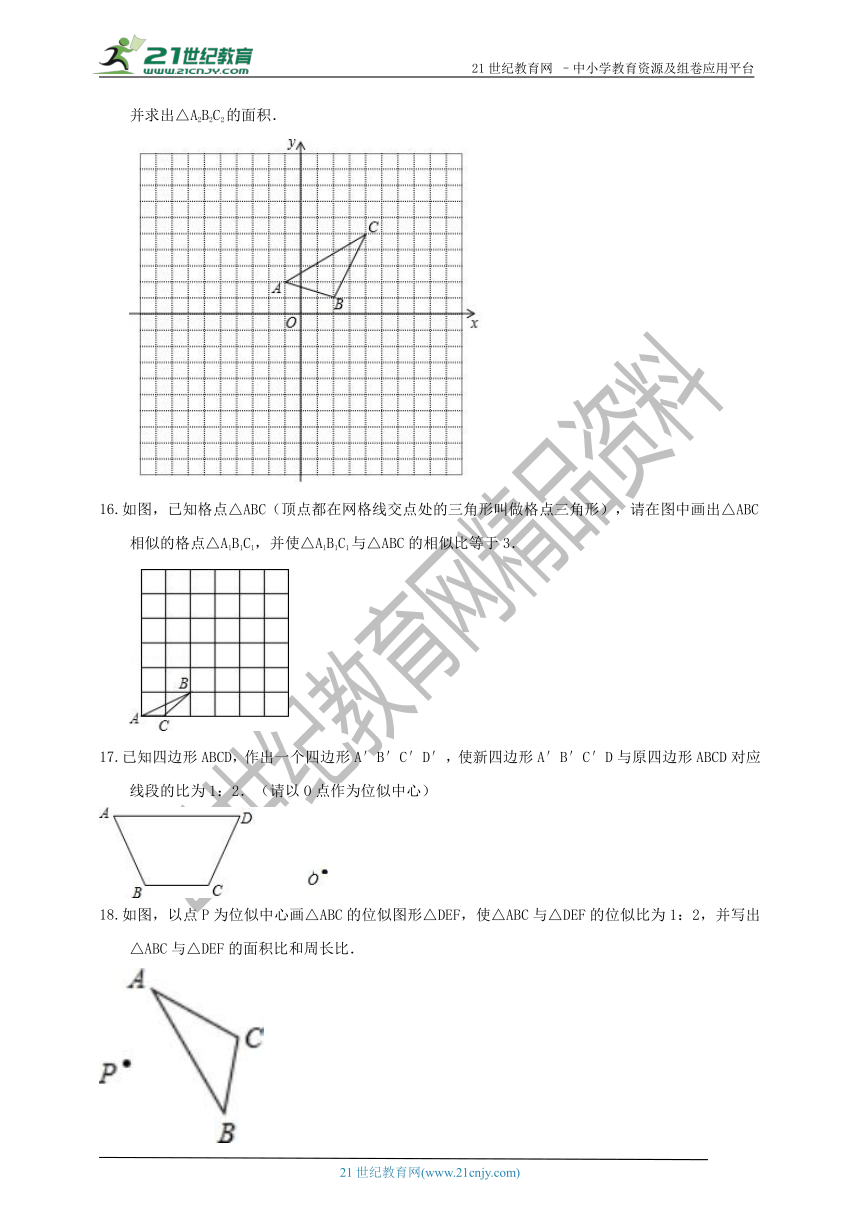
如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.
如图,已知格点△ABC(顶点都在网格线交点处的三角形叫做格点三角形),请在图中画出△ABC相似的格点△A1B1C1,并使△A1B1C1与△ABC的相似比等于3.
已知四边形ABCD,作出一个四边形A′B′C′D′,使新四边形A′B′C′D与原四边形ABCD对应线段的比为1:2.(请以O点作为位似中心)
如图,以点P为位似中心画△ABC的位似图形△DEF,使△ABC与△DEF的位似比为1:2,并写出△ABC与△DEF的面积比和周长比.
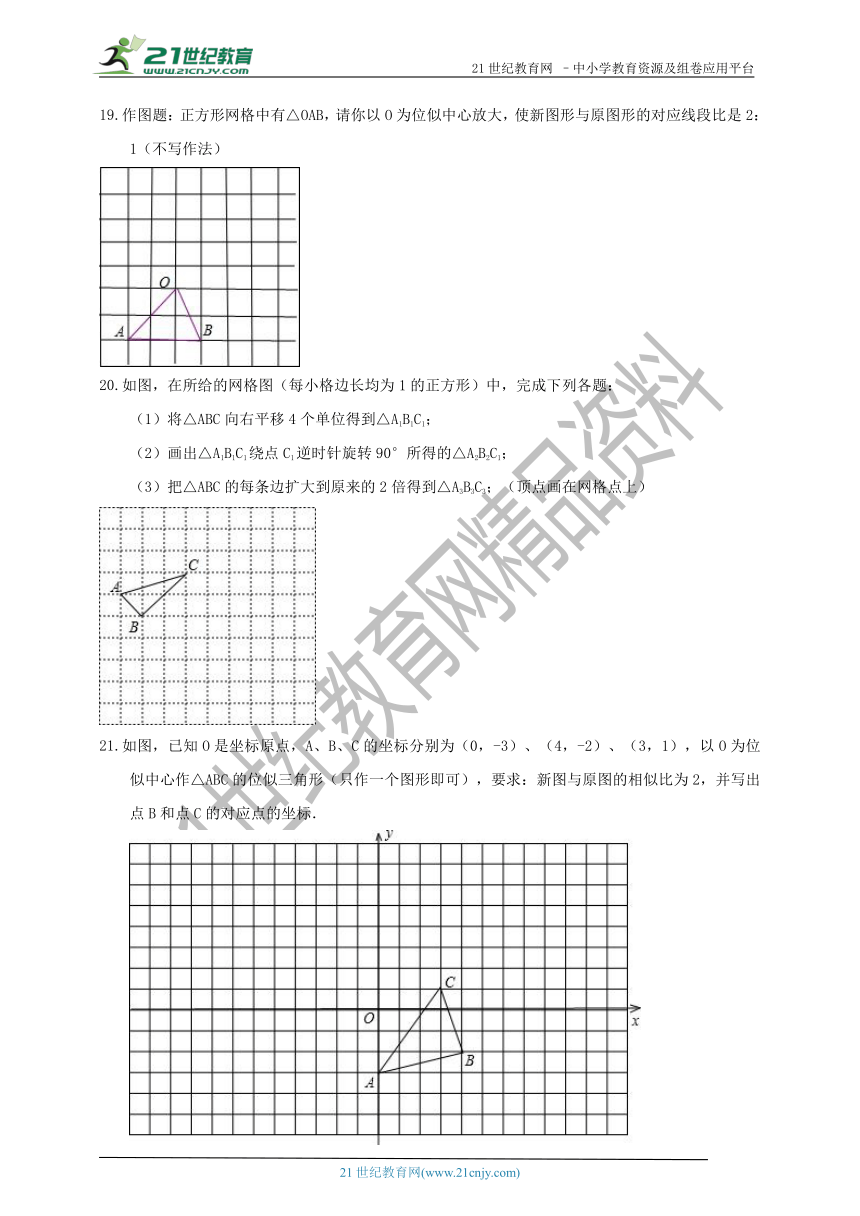
作图题:正方形网格中有△OAB,请你以O为位似中心放大,使新图形与原图形的对应线段比是2:1(不写作法)
如图,在所给的网格图(每小格边长均为1的正方形)中,完成下列各题:
(1)将△ABC向右平移4个单位得到△A1B1C1;
(2)画出△A1B1C1绕点C1逆时针旋转90°所得的△A2B2C1;
(3)把△ABC的每条边扩大到原来的2倍得到△A3B3C3;(顶点画在网格点上)
如图,已知O是坐标原点,A、B、C的坐标分别为(0,-3)、(4,-2)、(3,1),以O为位似中心作△ABC的位似三角形(只作一个图形即可),要求:新图与原图的相似比为2,并写出点B和点C的对应点的坐标.
答案解析
一 、选择题
1.【分析】 △ABC与△A1B1C1位似,△ABC与△A2B2C2位似,位似是特殊的相似,位似的两个图形一定形状相同,因而△A1B1C1与△A2B2C2相似,而△ABC与△A1B1C1的位似中心与,△ABC与△A2B2C2的位似不一定是同一个点,因而△A1B1C1与△A2B2C2相似但不一定位似.
解:∵△ABC与△A1B1C1位似,△ABC与△A2B2C2位似
∴△A1B1C1与△A2B2C2相似;△A1B1C1与△A2B2C2相似但不一定位似.
故选C.
【分析】根据位似变换的性质得出△ABC的边长放大到原来的2倍,FO=a,CF=a+1,CE=(a+1),进而得出点B的横坐标.
解:∵点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.
点B的对应点B′的横坐标是a,
∴FO=a,CF=a+1,
∴CE=(a+1),
∴点B的横坐标是:﹣(a+1)﹣1=﹣(a+3).
故选D.
【考点】位似变换;坐标与图形性质.
【分析】由以原点O为位似中心,相似比为,根据位似图形的性质,即可求得答案.
解:∵以原点O为位似中心,相似比为,A(6,3),
∴在第一象限内,点A的对应点坐标为:(2,1).
故选A.
【点评】此题考查了位似图形的变换.注意在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
【考点】命题与定理
【分析】根据二次根式的性质、位似图形的定义、正多边形的性质及三视图的概念逐一判断即可得.
解:A、=()2当a<0不成立,假命题;
B、位似图形在位似比为1时全等,假命题;
C、正多边形都是轴对称图形,真命题;
D、圆锥的主视图一定是等腰三角形,假命题;
故选:C.
【考点】位似变换,坐标与图形的性质
【分析】根据位似变换的性质计算即可.
解:点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,
则点P的对应点的坐标为(m×2,n×2)或(m×(-2),n×(-2)),即(2m,2n)或(-2m,-2n),
故选B.
点睛:本题考查的是位似变换、坐标与图形的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
【考点】位似图形的性质
【分析】利用位似图形的性质,结合两图形的位似比进而得出C点坐标.
解:∵以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,
∴端点C的横坐标和纵坐标都变为A点的横坐标和纵坐标的一半,
又∵A(6,8),
∴端点C的坐标为(3,4).
故选:C.
【点评】此题主要考查了位似图形的性质,利用两图形的位似比得出对应点横纵坐标关系是解题关键.
【考点】 位似变换;坐标与图形性质.
【分析】根据位似变换的性质得===,则PO=OA=2,然后写出P点坐标.
解:∵点B的坐标为(2,4),点E的坐标为(﹣1,2),
∴AB=4,OA=2,OD=2,
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,
∴===,
∴PO=OA=2,
∴P点坐标为(﹣2,0).
故选C.
点评:本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:两个图形必须是相似形;对应点的连线都经过同一点;对应边平行.
【考点】位似变换.
【分析】由△ABC 经过位似变换得到△DEF,点 O 是位似中心且 OA=AD,根据位似图形的性质, 即可得 AC∥DF,即可求得 AC:DF=OA:OD=1:2,然后根据相似三角形面积的比等于相似比的 平方,即可求得△ABC 与△DEF 的面积比.
解:∵△ABC 经过位似变换得到△DEF,点 O 是位似中心且 OA=AD,
∴AC∥DF,
∴△OAC∽△ODF,
∴AC:DF=OA:OD=1:2,
∴△ABC 与△DEF 的面积比是 1:4. 故选 C.
【点评】此题考查了位似图形的性质.注意掌握位似是相似的特殊形式,位似比等于相似比,其对 应的面积比等于相似比的平方.
二、填空题
【考点】位似变换;坐标与图形性质.
【分析】根据如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k进行解答.
解:∵以原点O为位似中心,将△OAB缩小为原来的,A(4,6),
则点A的对应点A′的坐标为(﹣2,﹣3)或(2,3),
故答案为:(﹣2,﹣3)或(2,3).
【点评】本题考查了位似变换:位似图形与坐标,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
【考点】位似变换;坐标与图形性质.
【分析】根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k解答.
解:∵点B的坐标为(﹣2,﹣4),以原点为位似中心将△ABC缩小,位似比为1:2,
∴点B的对应点的坐标为(1,2)或(﹣1,﹣2),
故答案为:(1,2)或(﹣1,﹣2).
【点评】本题考查的是位似变换的概念和性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
【考点】位似变换.
【分析】位似图形的主要特征是:每对位似对应点与位似中心共线.
解:直线AA′与直线BB′的交点坐标为(9,0),所以位似中心的坐标为(9,0).
【点评】本题考查位似中心的找法,各对应点所在直线的交点即为位似中心.
【考点】位似变换;坐标与图形性质.
【分析】根据位似变换的性质进行计算即可.
解:∵点A的坐标为(2,4),以原点O为位似中心,把这个三角形缩小为原来的,
∴点A′的坐标是(2×,4×),即(1,2),
故答案为:(1,2).
【考点】位似变换;坐标与图形性质.
【分析】根据题意得出D点坐标,再解直角三角形进而得出答案.
解:分别过A作AE⊥OB,CF⊥OB,
∵∠OCD=90°,∠AOB=60°,
∴∠ABO=∠CDO=30°,∠OCF=30°,
∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,点B的坐标是(6,0),
∴D(8,0),则DO=8,
故OC=4,
则FO=2,CF=CO cos30°=4×=2,
故点C的坐标是:(2,2).
故答案为:(2,2).
【点评】此题主要考查了位似变换,运用位似图形的性质正确解直角三角形是解题关键.
【考点】位似变换;坐标与图形性质.
【分析】根据位似图形的性质得出AO,DO的长,进而得出==,求出DE的长即可.
解:∵△ABC与DEF是位似图形,它们的位似中心恰好为原点,已知A点坐标为(1,0),D点坐标为(3,0),
∴AO=2,DO=5,
∴==,
∵AB=1.5,
∴DE=4.5.
故答案为:4.5.
【点评】此题主要考查了位似图形的性质以及坐标与图形的性质,根据已知点的坐标得出==是解题关键.
三、解答题
【考点】作图﹣位似变换;作图﹣轴对称变换.
【分析】(1)画出A、B、C关于x轴的对称点A1、B1、C1即可解决问题;
(2)连接OB延长OB到B2,使得OB=BB2,同法可得A2、C2,△A2B2C2就是所求三角形;
解:(1)如图所示,△A1B1C1就是所求三角形
(2)如图所示,△A2B2C2就是所求三角形
如图,分别过点A2、C2作y轴的平行线,过点B2作x轴的平行线,交点分别为E、F,
∵A(﹣1,2),B(2,1),C(4,5),△A2B2C2与△ABC位似,且位似比为2,
∴A2(﹣2,4),B2(4,2),C2(8,10),
∴=8×10﹣×6×2﹣×4×8﹣×6×10=28.
16.【考点】 作图—相似变换.
【分析】 利用相似三角形的性质,对应边的相似比相等,对应角相等,可以让各边长都放大到原来的3倍,得到新三角形.当然也可以缩小到原来3倍.
解:
【分析】以O为位似中心的四边形可以画2个,延长AO,BO,CO,DO根据相似比,在线段或其延长线上分别截取AO,BO,CO,DO的一半,②确定所作的位似图形的关键点A',B',C',D',再顺次连接所作各点,即可得到位似比为1:2的位似图形四边形A'B'C'D'.
解:以O为位似中心的四边形可以画2个,所画图形如下所示:
【分析】连接AP、BP和CP,并延长到2AP、2BP和2CP长度找到各点的对应点,顺次连接即可.
解:所画图形如下所示:
(4分)
△ABC与△DEF的面积比和周长比分别是1:4和1:2(6分)
【分析】画△OCD,根据题意位似中心已知为O,则延长AO,BO,根据相似比,确定所作的位似图形的关键点C、D,再顺次连接所作各点,即可得到放大一倍的图形△CDO;
解:如图:分别延长AO,BO到点C,D使OC=2AO,OD=2BO,
顺次连接即得△OCD
【分析】(1)先找出平移后的对应点A1,B1,C1的位置,然后顺次连接即可得出图形;
(2)分别找出点A、B、C绕点C1逆时针旋转90°后的对应点A2、B2的位置,然后顺次连接A2、B2、C1即可;
(3)利用原三角形各边长度,将各边扩大2倍得出△A3B3C3三边长,再利用顶点画在网格点上得出即可.
解:(1)将三角形对应顶点向右平移4个单位即可,如图所示;
(2)将△A1B1C1绕点C1逆时针旋转90°,得出对应点A2,B2,C1;如图所示;
(3)原三角形各边长度分别为:,2,,
将各边扩大2倍得出△A3B3C3三边长,如图所示.
【分析】延长AO到A′,使OA′=2AO,延长BO到B′,使OB′=2BO,延长CO到C′,使OC′=2CO,然后顺次连接A′、B′、C′即可得解;
或:延长OA到A′,使OA′=2AO,延长OB到B′,使OB′=2BO,延长OC到C′,使OC′=2CO,然后顺次连接A′、B′、C′即可得解.
解:如图所示,△A′B′C′即为所求作的三角形,
图1中,点B和点C的对应点B′、C′的坐标分别为(-8,4)、(-6,-2),
图2中,点B和点C的对应点B′、C′的坐标分别为(8,-4)、(6,2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
22.4 图形的位似变换同步作业
姓名:__________班级:__________考号:__________
一 、选择题
已知△ABC与△A1B1C1位似,△ABC与△A2B2C2位似,则( )
A. △A1B1C1与△A2B2C2全等
B. △A1B1C1与△A2B2C2位似
C. △A1B1C1与△A2B2C2相似但不一定位似
D. △A1B1C1与△A2B2C2不相似
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. B. C. D.
如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到新的线段,则点A的对应点坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
下列命题中真命题是( )
A.=()2一定成立 B.位似图形不可能全等
C.正多边形都是轴对称图形 D.圆锥的主视图一定是等边三角形
在平面直角坐标系中,点是线段上一点,以原点为位似中心把放大到原来的两倍,则点的对应点的坐标为( )
A. B. 或
C. D. 或
在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )
A.(5,1) B.(4,3) C.(3,4) D.(1,5)
如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(﹣1,2),则点P的坐标为( )
A. (﹣4,0) B. (﹣3,0) C. (﹣2,0) D. (﹣1.5,0)
如图,△ABC 经过位似变换得到△DEF,点 O 是位似中心且 OA=AD,则△ABC 与△DEF 的面 积比是( )
A.1:6 B.1:5 C.1:4 D.1:2
二、填空题
△OAB三个顶点的坐标分别为O(0,0),A(4,6),B(3,0),以O为位似中心,将△OAB缩小为原来的,得到△OA′B′,则点A的对应点A′的坐标为 .
已知在平面直角坐标系中,点A(﹣3,﹣1)、B(﹣2,﹣4)、C(﹣6,﹣5),以原点为位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为 .
如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是 .
如图,△ABO三个顶点的坐标分别为A(2,4),B(6,0),O(0,0),以原点O为位似中心,把这个三角形缩小为原来的,可以得到△A′B′O,已知点B′的坐标是(3,0),则点A′的坐标是 .
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是 .
( http: / / www. / " \o "中国教育出版网\" )
如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .
三、解答题
如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.
如图,已知格点△ABC(顶点都在网格线交点处的三角形叫做格点三角形),请在图中画出△ABC相似的格点△A1B1C1,并使△A1B1C1与△ABC的相似比等于3.
已知四边形ABCD,作出一个四边形A′B′C′D′,使新四边形A′B′C′D与原四边形ABCD对应线段的比为1:2.(请以O点作为位似中心)
如图,以点P为位似中心画△ABC的位似图形△DEF,使△ABC与△DEF的位似比为1:2,并写出△ABC与△DEF的面积比和周长比.
作图题:正方形网格中有△OAB,请你以O为位似中心放大,使新图形与原图形的对应线段比是2:1(不写作法)
如图,在所给的网格图(每小格边长均为1的正方形)中,完成下列各题:
(1)将△ABC向右平移4个单位得到△A1B1C1;
(2)画出△A1B1C1绕点C1逆时针旋转90°所得的△A2B2C1;
(3)把△ABC的每条边扩大到原来的2倍得到△A3B3C3;(顶点画在网格点上)
如图,已知O是坐标原点,A、B、C的坐标分别为(0,-3)、(4,-2)、(3,1),以O为位似中心作△ABC的位似三角形(只作一个图形即可),要求:新图与原图的相似比为2,并写出点B和点C的对应点的坐标.
答案解析
一 、选择题
1.【分析】 △ABC与△A1B1C1位似,△ABC与△A2B2C2位似,位似是特殊的相似,位似的两个图形一定形状相同,因而△A1B1C1与△A2B2C2相似,而△ABC与△A1B1C1的位似中心与,△ABC与△A2B2C2的位似不一定是同一个点,因而△A1B1C1与△A2B2C2相似但不一定位似.
解:∵△ABC与△A1B1C1位似,△ABC与△A2B2C2位似
∴△A1B1C1与△A2B2C2相似;△A1B1C1与△A2B2C2相似但不一定位似.
故选C.
【分析】根据位似变换的性质得出△ABC的边长放大到原来的2倍,FO=a,CF=a+1,CE=(a+1),进而得出点B的横坐标.
解:∵点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.
点B的对应点B′的横坐标是a,
∴FO=a,CF=a+1,
∴CE=(a+1),
∴点B的横坐标是:﹣(a+1)﹣1=﹣(a+3).
故选D.
【考点】位似变换;坐标与图形性质.
【分析】由以原点O为位似中心,相似比为,根据位似图形的性质,即可求得答案.
解:∵以原点O为位似中心,相似比为,A(6,3),
∴在第一象限内,点A的对应点坐标为:(2,1).
故选A.
【点评】此题考查了位似图形的变换.注意在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
【考点】命题与定理
【分析】根据二次根式的性质、位似图形的定义、正多边形的性质及三视图的概念逐一判断即可得.
解:A、=()2当a<0不成立,假命题;
B、位似图形在位似比为1时全等,假命题;
C、正多边形都是轴对称图形,真命题;
D、圆锥的主视图一定是等腰三角形,假命题;
故选:C.
【考点】位似变换,坐标与图形的性质
【分析】根据位似变换的性质计算即可.
解:点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,
则点P的对应点的坐标为(m×2,n×2)或(m×(-2),n×(-2)),即(2m,2n)或(-2m,-2n),
故选B.
点睛:本题考查的是位似变换、坐标与图形的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
【考点】位似图形的性质
【分析】利用位似图形的性质,结合两图形的位似比进而得出C点坐标.
解:∵以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,
∴端点C的横坐标和纵坐标都变为A点的横坐标和纵坐标的一半,
又∵A(6,8),
∴端点C的坐标为(3,4).
故选:C.
【点评】此题主要考查了位似图形的性质,利用两图形的位似比得出对应点横纵坐标关系是解题关键.
【考点】 位似变换;坐标与图形性质.
【分析】根据位似变换的性质得===,则PO=OA=2,然后写出P点坐标.
解:∵点B的坐标为(2,4),点E的坐标为(﹣1,2),
∴AB=4,OA=2,OD=2,
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,
∴===,
∴PO=OA=2,
∴P点坐标为(﹣2,0).
故选C.
点评:本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:两个图形必须是相似形;对应点的连线都经过同一点;对应边平行.
【考点】位似变换.
【分析】由△ABC 经过位似变换得到△DEF,点 O 是位似中心且 OA=AD,根据位似图形的性质, 即可得 AC∥DF,即可求得 AC:DF=OA:OD=1:2,然后根据相似三角形面积的比等于相似比的 平方,即可求得△ABC 与△DEF 的面积比.
解:∵△ABC 经过位似变换得到△DEF,点 O 是位似中心且 OA=AD,
∴AC∥DF,
∴△OAC∽△ODF,
∴AC:DF=OA:OD=1:2,
∴△ABC 与△DEF 的面积比是 1:4. 故选 C.
【点评】此题考查了位似图形的性质.注意掌握位似是相似的特殊形式,位似比等于相似比,其对 应的面积比等于相似比的平方.
二、填空题
【考点】位似变换;坐标与图形性质.
【分析】根据如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k进行解答.
解:∵以原点O为位似中心,将△OAB缩小为原来的,A(4,6),
则点A的对应点A′的坐标为(﹣2,﹣3)或(2,3),
故答案为:(﹣2,﹣3)或(2,3).
【点评】本题考查了位似变换:位似图形与坐标,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
【考点】位似变换;坐标与图形性质.
【分析】根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k解答.
解:∵点B的坐标为(﹣2,﹣4),以原点为位似中心将△ABC缩小,位似比为1:2,
∴点B的对应点的坐标为(1,2)或(﹣1,﹣2),
故答案为:(1,2)或(﹣1,﹣2).
【点评】本题考查的是位似变换的概念和性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
【考点】位似变换.
【分析】位似图形的主要特征是:每对位似对应点与位似中心共线.
解:直线AA′与直线BB′的交点坐标为(9,0),所以位似中心的坐标为(9,0).
【点评】本题考查位似中心的找法,各对应点所在直线的交点即为位似中心.
【考点】位似变换;坐标与图形性质.
【分析】根据位似变换的性质进行计算即可.
解:∵点A的坐标为(2,4),以原点O为位似中心,把这个三角形缩小为原来的,
∴点A′的坐标是(2×,4×),即(1,2),
故答案为:(1,2).
【考点】位似变换;坐标与图形性质.
【分析】根据题意得出D点坐标,再解直角三角形进而得出答案.
解:分别过A作AE⊥OB,CF⊥OB,
∵∠OCD=90°,∠AOB=60°,
∴∠ABO=∠CDO=30°,∠OCF=30°,
∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,点B的坐标是(6,0),
∴D(8,0),则DO=8,
故OC=4,
则FO=2,CF=CO cos30°=4×=2,
故点C的坐标是:(2,2).
故答案为:(2,2).
【点评】此题主要考查了位似变换,运用位似图形的性质正确解直角三角形是解题关键.
【考点】位似变换;坐标与图形性质.
【分析】根据位似图形的性质得出AO,DO的长,进而得出==,求出DE的长即可.
解:∵△ABC与DEF是位似图形,它们的位似中心恰好为原点,已知A点坐标为(1,0),D点坐标为(3,0),
∴AO=2,DO=5,
∴==,
∵AB=1.5,
∴DE=4.5.
故答案为:4.5.
【点评】此题主要考查了位似图形的性质以及坐标与图形的性质,根据已知点的坐标得出==是解题关键.
三、解答题
【考点】作图﹣位似变换;作图﹣轴对称变换.
【分析】(1)画出A、B、C关于x轴的对称点A1、B1、C1即可解决问题;
(2)连接OB延长OB到B2,使得OB=BB2,同法可得A2、C2,△A2B2C2就是所求三角形;
解:(1)如图所示,△A1B1C1就是所求三角形
(2)如图所示,△A2B2C2就是所求三角形
如图,分别过点A2、C2作y轴的平行线,过点B2作x轴的平行线,交点分别为E、F,
∵A(﹣1,2),B(2,1),C(4,5),△A2B2C2与△ABC位似,且位似比为2,
∴A2(﹣2,4),B2(4,2),C2(8,10),
∴=8×10﹣×6×2﹣×4×8﹣×6×10=28.
16.【考点】 作图—相似变换.
【分析】 利用相似三角形的性质,对应边的相似比相等,对应角相等,可以让各边长都放大到原来的3倍,得到新三角形.当然也可以缩小到原来3倍.
解:
【分析】以O为位似中心的四边形可以画2个,延长AO,BO,CO,DO根据相似比,在线段或其延长线上分别截取AO,BO,CO,DO的一半,②确定所作的位似图形的关键点A',B',C',D',再顺次连接所作各点,即可得到位似比为1:2的位似图形四边形A'B'C'D'.
解:以O为位似中心的四边形可以画2个,所画图形如下所示:
【分析】连接AP、BP和CP,并延长到2AP、2BP和2CP长度找到各点的对应点,顺次连接即可.
解:所画图形如下所示:
(4分)
△ABC与△DEF的面积比和周长比分别是1:4和1:2(6分)
【分析】画△OCD,根据题意位似中心已知为O,则延长AO,BO,根据相似比,确定所作的位似图形的关键点C、D,再顺次连接所作各点,即可得到放大一倍的图形△CDO;
解:如图:分别延长AO,BO到点C,D使OC=2AO,OD=2BO,
顺次连接即得△OCD
【分析】(1)先找出平移后的对应点A1,B1,C1的位置,然后顺次连接即可得出图形;
(2)分别找出点A、B、C绕点C1逆时针旋转90°后的对应点A2、B2的位置,然后顺次连接A2、B2、C1即可;
(3)利用原三角形各边长度,将各边扩大2倍得出△A3B3C3三边长,再利用顶点画在网格点上得出即可.
解:(1)将三角形对应顶点向右平移4个单位即可,如图所示;
(2)将△A1B1C1绕点C1逆时针旋转90°,得出对应点A2,B2,C1;如图所示;
(3)原三角形各边长度分别为:,2,,
将各边扩大2倍得出△A3B3C3三边长,如图所示.
【分析】延长AO到A′,使OA′=2AO,延长BO到B′,使OB′=2BO,延长CO到C′,使OC′=2CO,然后顺次连接A′、B′、C′即可得解;
或:延长OA到A′,使OA′=2AO,延长OB到B′,使OB′=2BO,延长OC到C′,使OC′=2CO,然后顺次连接A′、B′、C′即可得解.
解:如图所示,△A′B′C′即为所求作的三角形,
图1中,点B和点C的对应点B′、C′的坐标分别为(-8,4)、(-6,-2),
图2中,点B和点C的对应点B′、C′的坐标分别为(8,-4)、(6,2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
